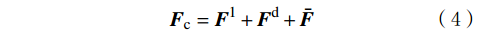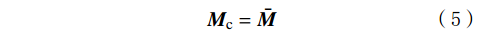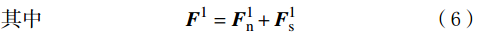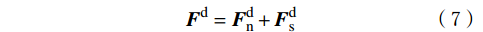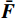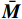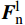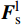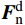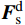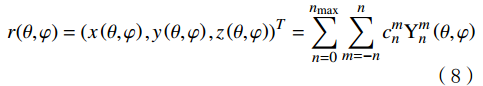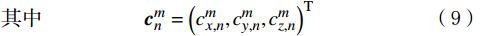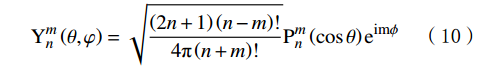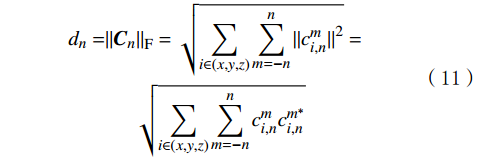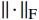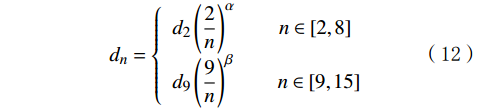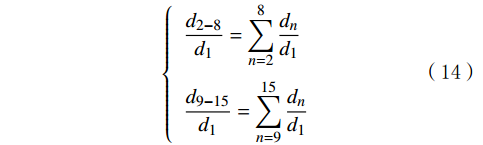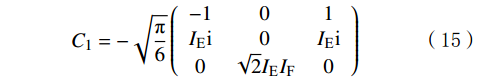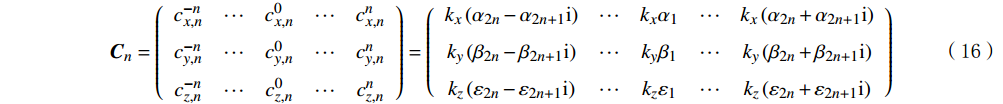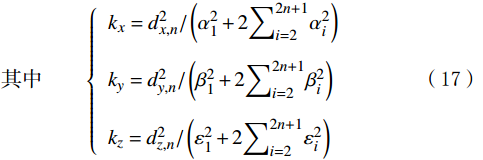Digital Core Construction Methods for High Stress in Deep and Ultra-Deep Oil and Gas Reservoirs
-
摘要:
深层超深层油气藏由于埋藏深，其地应力达200 MPa，会显著改变储层岩石孔隙的微观结构。数字岩心是孔隙尺度数值模拟的重要载体，但是现有数字岩心重构方法是基于常温常压下岩心的扫描图像重构，不能反映高应力下的孔隙结构。为此，提出了一种基于离散元法考虑高应力影响的数字岩心重构方法。首先，采用分水岭算法分割CT图像，利用球面谐波分析方法建立轮廓数据库，并在PFC3D中建立Clump（团簇）模板库；然后，根据孔隙度和粒径分布使用模板库中的Clump建立离散元模型，并用两点相关和线性路径相关函数曲线评价模型的准确性；随后，标定颗粒间微观力学参数，并加载应力模拟得到不同应力下的数字岩心；最后，分析了不同应力下数字岩心的孔隙几何拓扑结构，计算孔隙度和渗透率。以Bentheim砂岩为例，构建了其不同应力下的数字岩心，研究结果表明，应力增大，导致孔隙和喉道半径缩小、喉道伸长、连通性变差、孔隙度和渗透率减小。研究结果为深层超深层油气藏孔隙尺度模拟提供了技术途径。
-
关键词:
- 油气藏 /
- 深层超深层；数字岩心重构 /
- 离散元法 /
- 孔隙几何拓扑结构 /
- 渗透率
Abstract:Deep and ultra-deep oil and gas reservoirs buried at significant depths and subjected to ground stresses of 200 MPa, undergo notable changes in the pore microstructure of reservoir rocks. Digital core modeling serves as a crucial tool for pore-scale numerical simulations. However, current digital core reconstruction methods are based on scanning image reconstruction under normal temperature and pressure conditions and thus they fail to reflect the pore structure under high pressure conditions. Therefore, a digital core reconstruction method based on the discrete element method (DEM) was proposed by considering the effect of high stress. Initially, the watershed algorithm was employed to segment computed tomography (CT) images, and the contour database was established by the spherical harmonic analysis method. The Clump template library was established in PFC3D. Then, according to porosity and particle size distribution, the Clump in template library was used to build a discrete element model. After, the accuracy of the model was evaluated via calculations of two-point correlation and linear path correlation function curves. Next, the micromechanical parameters between particles were calibrated, enabling simulation of the digital core under varying stress conditions. Finally, the pore geometry topology of the digital core under different stresses was analyzed, and porosity and permeability were calculated. Bentheim sandstone was taken as an example to construct digital cores under different stresses.. The research results show that high stress leads to reduced pore and throat radius, elongated throats, diminished connectivity, and lower porosity and permeability. The results provide technical support for pore-scale simulations of deep and ultra-deep oil and gas reservoirs..
-
随着我国中浅层油气藏开发进入中后期，油气勘探目的层逐渐转向深层（大于 4500 m）和超深层（大于6000 m）[1–4]，深层超深层油气藏具有高温、高压和高应力的特点[5–6]，显著影响储层岩石孔隙结构[7]，从而影响油气渗流[8–9]。数字岩心是数值模拟研究油气微观渗流规律的载体，重构数字岩心是开展油气微观渗流数值模拟的重要步骤。现有重构方法分为物理实验法和数值模拟法，其中物理实验法是指用CT等成像技术结合图像处理算法构建三维数字岩心[10–11]；数值模拟法包括随机模拟算法[12]、过程模拟法[13–14]和深度学习算法[15–17]，其中随机模拟算法、深度学习算法均依赖CT扫描图像，但是现有CT扫描时承压能力仅为30～40 MPa，不能满足深层高应力的需求[18]。过程模拟法则通过模拟岩石颗粒的沉积、压实和成岩过程，构建能反映应力影响的数字岩心。离散元法（discrete element method, DEM）是实现过程模拟法的手段[19–21]，DEM建模需要解决以下问题：一是分割CT图像中相互接触的颗粒，通常采用分水岭算法[22]；二是颗粒轮廓的提取与分析，通常用一个连续函数表示轮廓曲面，包括超二次椭球函数[23]、非均匀有理B样条函数[24]、傅里叶级数[25]和球面谐波函数[26]，其中在三维情况下应用最为成熟的是球面谐波函数分析[27]；三是将颗粒轮廓转化为用于离散元法计算的颗粒，一种是重叠离散元颗粒簇（overlapping discrete element cluster, ODEC）方法填充轮廓形成的clump（团簇）作为颗粒计算[28-30]，另一种是直接使用提取的轮廓作为颗粒计算，其中前者使用最为广泛[31]。
根据上述分析，笔者提出了基于离散元法考虑深层超深层油气藏高应力影响的数字岩心构建方法。首先，基于常温常压下的扫描结果，采用球面谐波函数分析得到形状和粒径分布，并转化为Clump构建模板库，根据粒径分布从模板库中选取Clump进行建模，实现常温常压数字岩心从图像到离散元模型的转化；然后，施加应力边界模拟深层超深层的高地应力，并使用PFC3D进行模拟计算；最后，根据颗粒的位置和半径利用体素化算法转化为数字岩心，分析了数字岩心孔隙度、孔隙结构和渗透率在不同应力下的变化规律，并利用Bentheim算例验证了考虑高应力影响的数字岩心重构方法的可行性。研究结果为深层超深层油气藏孔隙尺度模拟提供了技术途径。
1. 数字岩心构建方法及原理
1.1 离散元法理论基础
离散元法的基本原理是使用相互接触的颗粒建模，每个颗粒的运动均符合牛顿第二定律，采用显式中心差分格式求解每个颗粒的运动，由各颗粒的运动得到整体力学性质。颗粒i的平动和转动方程分别为：
{m}_{i}\frac{{\rm{d}}{\boldsymbol{v}}_{i}}{{\rm{d}}t}+{\beta }_{\mathrm{g}}{\boldsymbol{v}}_{i}\left(t\right)={\boldsymbol{F}}_{\mathrm{t}i} (1) {I}_{i}\frac{{\rm{d}}{\boldsymbol{\omega }}_{i}}{{\rm{d}}t}+{\beta }_{\mathrm{g}}{{\boldsymbol{\omega}} }_{i}\left(t\right)={\boldsymbol{M}}_{i} (2) 式中：mi为第i个颗粒的质量，kg；Ii为第i个颗粒分转动惯量，kg·m²；vi为第i个颗粒速度，m/s； ωi为第i个颗粒角速度，rad/s；βg为整体阻尼，kg/s；Fti为第i个颗粒合外力，N；Mi为第i个颗粒合力矩，N·m。
使用显式有限差分算法更新每个颗粒的速度和转动角度，并更新颗粒的位置。显式方法中，时间步的选择是保证数值稳定性的关键，PFC3D中定义了临界时间步长：
\Delta {t}_{\text{crit}}=\sqrt{\frac{m}{k}} (3) 式中：Δtcrit为临界时间步长，s；m为颗粒的质量，kg；k为接触弹簧的刚度，N/m。
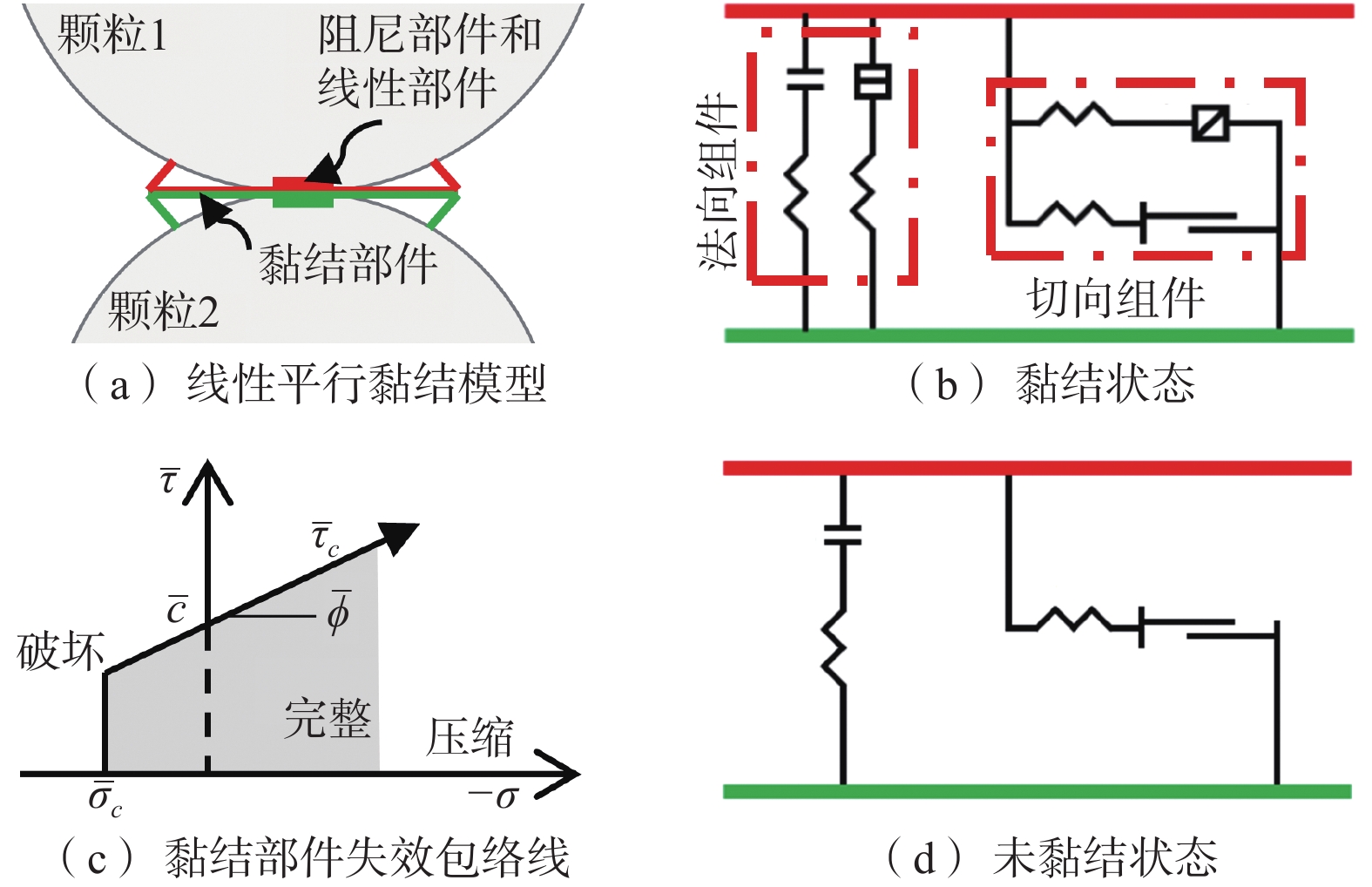
颗粒位置更新后，需要重新确定颗粒的接触关系，常用的接触搜索算法为基于网格的接触搜索算法。确定新的接触关系后，根据颗粒之间的本构关系计算颗粒间的接触力。模拟岩石材料的力学行为常用的接触模型为线性平行黏结模型（见图1）。
线性平行黏结模型中，颗粒间接触力和力矩的计算公式为：
{\boldsymbol{F}}_{\mathrm{c}}={\boldsymbol{F}}^{1}+{\boldsymbol{F}}^{\mathrm{d}}+\bar{\boldsymbol{F}} (4) {\boldsymbol{M}}_{\mathrm{c}}=\bar{\boldsymbol{M}} (5) \,其中\qquad\qquad\qquad\;\; \;\;{\boldsymbol{F}}^{1}={\boldsymbol{F}}_{\mathrm{n}}^{1}+{\boldsymbol{F}}_{\mathrm{s}}^{1}\qquad\qquad (6) {\boldsymbol{F}}^{\mathrm{d}}={\boldsymbol{F}}_{\mathrm{n}}^{\mathrm{d}}+{\boldsymbol{F}}_{\mathrm{s}}^{\mathrm{d}} (7) 式中：Fc为接触力，N；Mc为接触力矩，N·m；Fl为线性力，N；Fd为阻尼力，N；
{\bar {\boldsymbol{F}}} 为平行黏结力，N；{\bar {\boldsymbol{M}} } 为平行黏结力矩，N·m；{\boldsymbol{F}}_{\mathrm{n}}^{\mathrm{l}} 为法向线性力，N；{\boldsymbol{F}}_{\mathrm{s}}^{\mathrm{l }} 为切向线性力，N；{\boldsymbol{F}}_{\mathrm{n}}^{\mathrm{d}} 为法向阻尼力，N；{\boldsymbol{F}}_{\mathrm{s}}^{\mathrm{d}} 为切向阻尼力，N。1.2 球面谐波函数分析及颗粒轮廓重构
球面谐波函数（spherical harmonic function）分析是傅里叶级数展开分析的一种，是用球面谐波函数线性组合表达式确定的闭合曲面来表征颗粒轮廓形状：
\mathit{r}(\theta,\varphi)=(x\left(\theta,\varphi\right),y\left(\theta,\varphi\right),z\left(\theta,\varphi\right))^T=\sum_{n=0}^{n_{\mathrm{m}\mathrm{a}\mathrm{x}}}\sum_{m=-n}^n\mathit{c}_n^m\mathrm{Y}_n^m\left(\theta,\varphi\right) (8) \,其中 \qquad \qquad\;\;\;\;{\boldsymbol{c}}_{n}^{m}={\left({c}_{x,n}^{m},{c}_{y,n}^{m},{c}_{z,n}^{m}\right)}^{{\rm{T}}} \qquad\qquad (9) \mathrm{Y}_n^m\left(\theta,\varphi\right)=\sqrt{\frac{\left(2n+1\right)\left(n-m\right)!}{4\text{π}\left(n+m\right)!}}\mathrm{P}_n^m\left(\cos\theta\right)\rm{e}^{im\phi} (10) 式中： nmax表示最高阶数，一般取为15；n为阶数；m为次数；
{\boldsymbol{c}}^m_n 为系数矩阵；\mathrm{Y}_n^m 为球面谐波函数；\mathrm{P}_n^m 表示关联勒让德函数。Wei Deheng等人[24]提出了一种系数矩阵的重构算法。首先，定义球面描述符：
\begin{aligned}{d}_{n}=&{\|{\boldsymbol{C}}_{n}\|}_{{\rm{F}}}=\sqrt{\sum _{i\in \left(x,y,z\right)}\sum _{m=-n}^{n}{\|{c}_{i,n}^{m}\|}^{2}}=\\ &\quad\;\;\sqrt{\sum _{i\in \left(x,y,z\right)}\sum _{m=-n}^{n}{c}_{i,n}^{m}{c}_{i,n}^{{m}^{\mathrm{*}}}} \end{aligned} (11) 式中：Cn表示阶数为n的所有系数组成的矩阵；
{\|\cdot \|}_{{\rm{F}}} 表示Frobenius范数；*表示共轭转置。用幂函数拟合颗粒的球面描述符与阶数n的关系，得到参数α和β：
d_{\rm{\mathit{n}}}=\left\{\begin{array}{l}d_2\left(\dfrac{2}{n}\right)^{\alpha}\qquad n\in\left[\mathrm{2,8}\right] \\ d_9\left(\dfrac{9}{n}\right)^{\beta}\qquad n\in\left[\mathrm{9,15}\right]\end{array}\right. (12) 随后，分析球面描述符主成分，定义4个旋转不变球面谐波因子：
\left\{\begin{array}{l}I_\text{E}=\dfrac{p_2}{p_1} \\ I_\text{F}=\dfrac{p_3}{p_2}\end{array}\ \ \ \ \ \quad\left(p_1 > p_2 > p_3\right)\right. (13) \left\{\begin{array}{l}\dfrac{{d}_{2-8}}{{d}_{1}}=\displaystyle\sum _{n=2}^{8}\dfrac{{d}_{n}}{{d}_{1}}\\ \dfrac{{d}_{9-15}}{{d}_{1}}=\displaystyle\sum _{n=9}^{15}\dfrac{{d}_{n}}{{d}_{1}}\end{array}\right. (14) 式中：IE为延伸指数；IF为平面指数；d2-8/d1表征颗粒圆度；d9-15/d1表征颗粒的细观形状特征。
最后，根据旋转不变球面谐波因子分布规律重构系数矩阵，使用IE和IF计算C1：
{\mathit{C}}_{1}=-\sqrt{\frac{{\text{π}} }{6}}\left(\begin{array}{ccc}-1& 0& 1\\ I_\text{E} \text{i}& 0& I_\text{E} \text{i}\\ 0& \sqrt{2}I_\text{E} I_\text{F}& 0\end{array}\right) (15) 根据d2-8/d1和d9-15/d1的值结合式（12）计算d2～d15，并假设3个维度上的球面描述符相等，构造相应的系数矩阵C2～C15：
{\boldsymbol{C}}_{n}=\left(\begin{array}{ccccc}{c}_{x,n}^{-n}& \cdots & {c}_{x,n}^{0}& \cdots & {c}_{x,n}^{n}\\ {c}_{y,n}^{-n}& \cdots & {c}_{y,n}^{0}& \cdots & {c}_{y,n}^{n}\\ {c}_{z,n}^{-n}& \cdots & {c}_{z,n}^{0}& \cdots & {c}_{z,n}^{n}\end{array}\right)=\left(\begin{array}{ccccc}{k}_{x}\left({\alpha }_{2n}-{\alpha }_{2n+1}\text{i}\right)& \cdots & {k}_{x}{\alpha }_{1}& \cdots & {k}_{x}\left({\alpha }_{2n}+{\alpha }_{2n+1}\text{i}\right)\\ {k}_{y}\left({\beta }_{2n}-{\beta }_{2n+1}\text{i}\right)& \cdots & {k}_{y}{\beta }_{1}& \cdots & {k}_{y}\left({\beta }_{2n}+{\beta }_{2n+1}\text{i}\right)\\ {k}_{z}\left({\varepsilon }_{2n}-{\varepsilon }_{2n+1}\text{i}\right)& \cdots & {k}_{z}{\varepsilon }_{1}& \cdots & {k}_{z}\left({\varepsilon }_{2n}+{\varepsilon }_{2n+1}\text{i}\right)\end{array}\right) (16) \,其中\qquad \left\{\begin{array}{l}{k}_{x}={d}_{x,n}^{2}/\left({\alpha }_{1}^{2}+2{\displaystyle\sum }_{i=2}^{2n+1}{\alpha }_{i}^{2}\right)\\ {k}_{y}={d}_{y,n}^{2}/\left({\beta }_{1}^{2}+2{\displaystyle\sum }_{i=2}^{2n+1}{\beta }_{i}^{2}\right)\\ {k}_{z}={d}_{z,n}^{2}/\left({\varepsilon }_{1}^{2}+2{\displaystyle\sum }_{i=2}^{2n+1}{\varepsilon }_{i}^{2}\right)\end{array}\right. (17) 式中：αi, βi, εi为0～1之间符合均匀分布的随机数，kx, ky和kz为归一化因子。
1.3 离散元法数字岩心构建流程及评价方法
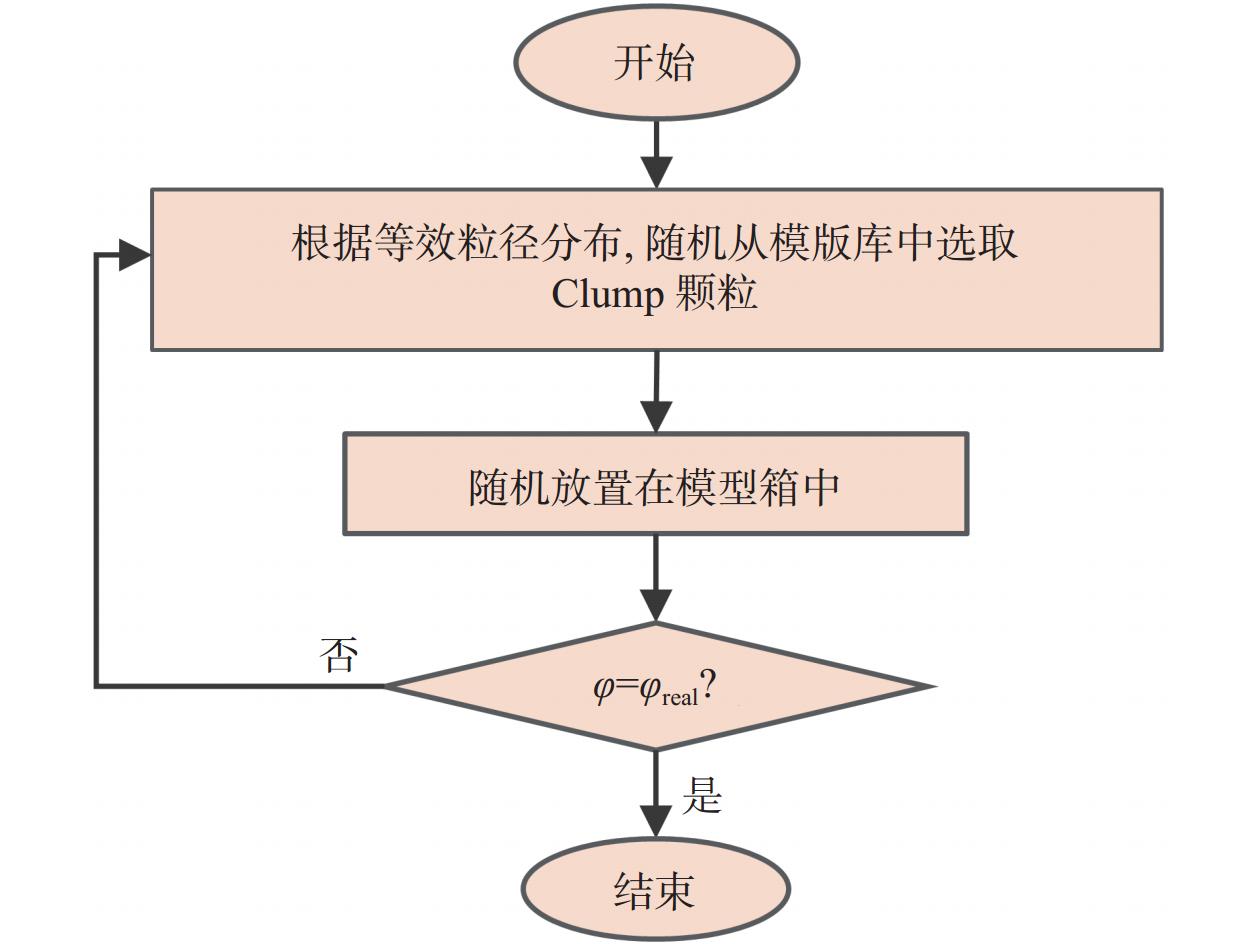
基于离散元法重构高应力影响的数字岩心构建方法为：1）建立常温常压数字岩心离散元模型，先使用1.2节方法构造符合实际形状特征的数据库，并转化为Clump模板库，再根据粒径分布从模板库中随机选取颗粒建模，并判断孔隙度是否达到实际岩心的孔隙度，不断调整每种Clump的比例，直至达到真实孔隙度（见图2），最后对比重构结果与实际岩心的两点相关函数曲线和线性路径相关函数曲线；2）在模型的边界施加应力，并在PFC3D中模拟伺服加载至设定应力，模拟深层超深层储层岩石不同方向受到的应力；3）将离散元模型体素化为数字岩心，提取孔隙网络模型分析孔隙几何拓扑结构，计算孔隙度和渗透率。
![]()
图 2 常温常压数字岩心离散元建模流程Figure 2. Flowchart of digital core modeling at normal temperature and pressure by DEM2. 常温常压数字岩心离散元建模
Bentheim砂岩具有完善的CT扫描图像和力学实验数据，可以用来验证考虑高应力数字岩心构建方法的可行性。通过颗粒分割与提取、球面谐波分析重构颗粒形状，将岩心图像转化为颗粒，用于离散元建模，得到常温常压下数字岩心的离散元模型。
2.1 颗粒分割与提取
选用的Bentheim砂岩图像大小为891×891×1400，分辨率为4.901 46 μm。为消除边界效应，选取300×300×600体素的区域作为分析对象，孔隙度为22.95%，使用分水岭算法处理图像，分割相互接触的颗粒并保存每个颗粒的所有体素，共提取500个完整颗粒。
2.2 球面谐波分析重构颗粒形状
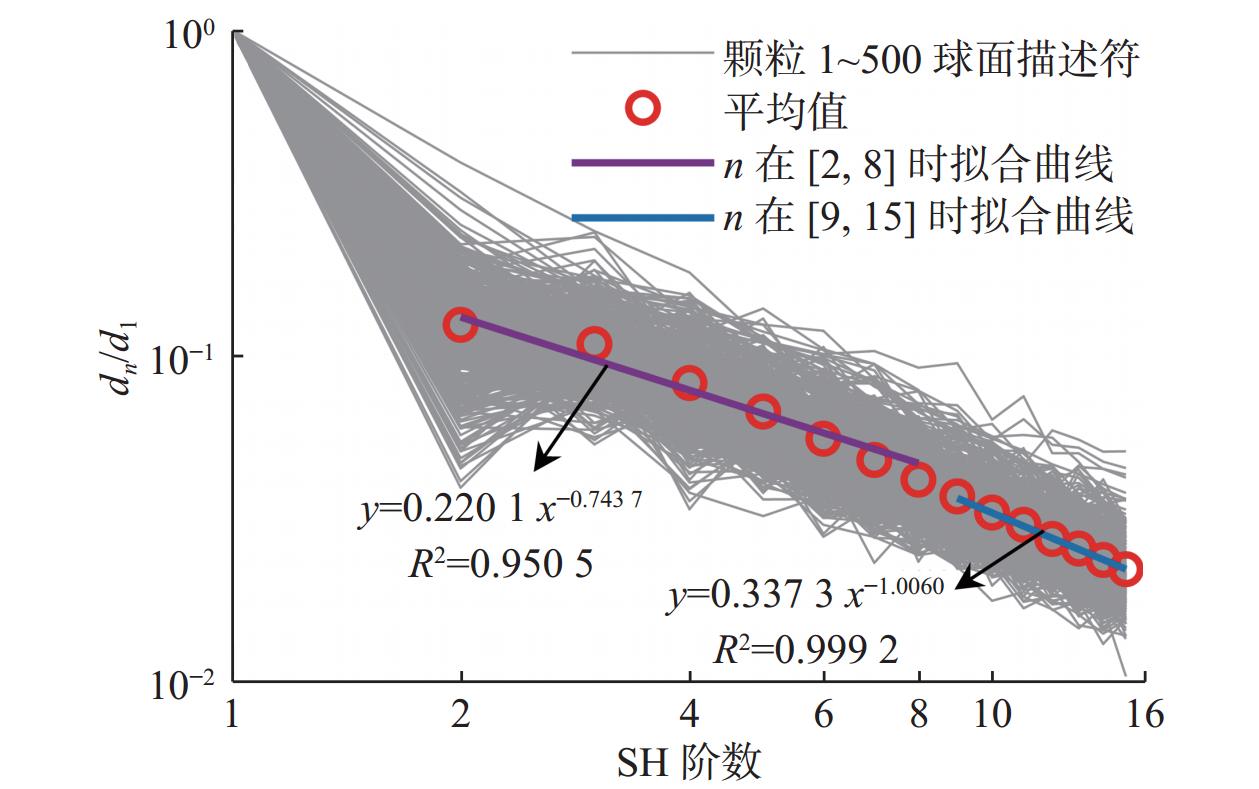
提取图像中每个颗粒所有体素后，首先对每个颗粒进行球面谐波展开，阶数设置为15，计算每个颗粒的球面谐波函数系数矩阵，并保存相应的图形文件和系数矩阵；接着，分析了颗粒的等效粒径、纵横比（IE和IF的平均值）、球度、凸度和圆度的分布曲线（见图3），为Clump模板库及常温常压数字岩心离散元建模提供依据。
![]()
图 3 样品粒径及颗粒形状分析结果Figure 3. Analysis results of particle size and particle shapes of the sample接着分析球面描述符与阶数之间的关系，拟合得到式（12）中的参数α和β。在双对数坐标系中绘制了颗粒1～500的球面描述符与球面谐波函数阶数（SH阶数）之间的关系曲线（见图4），用幂函数进行拟合，拟合结果为：α = 0.743 7，β = 1.006。
![]()
图 4 球面描述符与SH阶数的关系曲线Figure 4. Relationship between the spherical descriptor and SH degree根据形状分析结果，设置不同比例的IE、IF、d2-8/d1和d9-15/d1，结合参数α、β的拟合结果重构球面谐波函数系数矩阵C，得到符合实际形状分布特征的颗粒轮廓数据库，数据库大小为50。使用ODEC方法转化为PFC3D中的Clump颗粒，形成模板库用于后续建模。
2.3 常温常压数字岩心的离散元建模
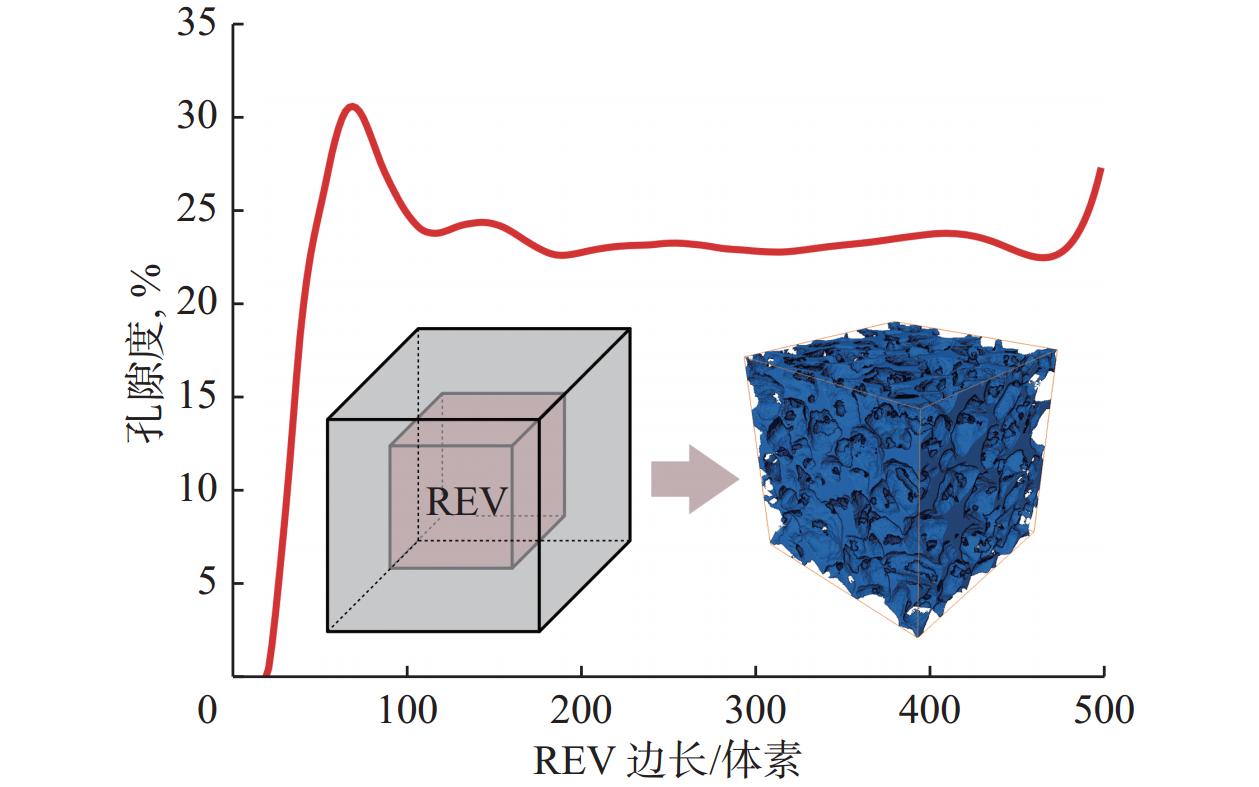
通过以上步骤，将常温常压下的数字岩心转化为离散元颗粒，随后根据离散元建模方法，实现常温常压数字岩心从图像到离散元模型的转化。常温常压数字岩心的离散元模型如图5（a）所示，模型尺寸为1.5 mm×1.5 mm×1.5 mm，使用边长为3 μm的体素对模型进行体素化，转化为数字岩心，体素尺寸为500×500×500（见图5（b））。从图5（b）可以看出，孔隙度受到边界效应的影响，边界处的孔隙度大，内部孔隙度小。
![]()
图 5 常温常压数字岩心离散元建模结果Figure 5. Results of digital core modeling at normal temperature and pressure by DEM不同表征单元体（representative elementary volume，REV）边长与孔隙度间的关系如图6所示，可以发现REV边长为200～400时，孔隙度较分布平缓。综合以上2个方面，选择REV为300，体素范围100～400，此时模型孔隙度为22.88%，与真实岩心的相对误差为0.30%。
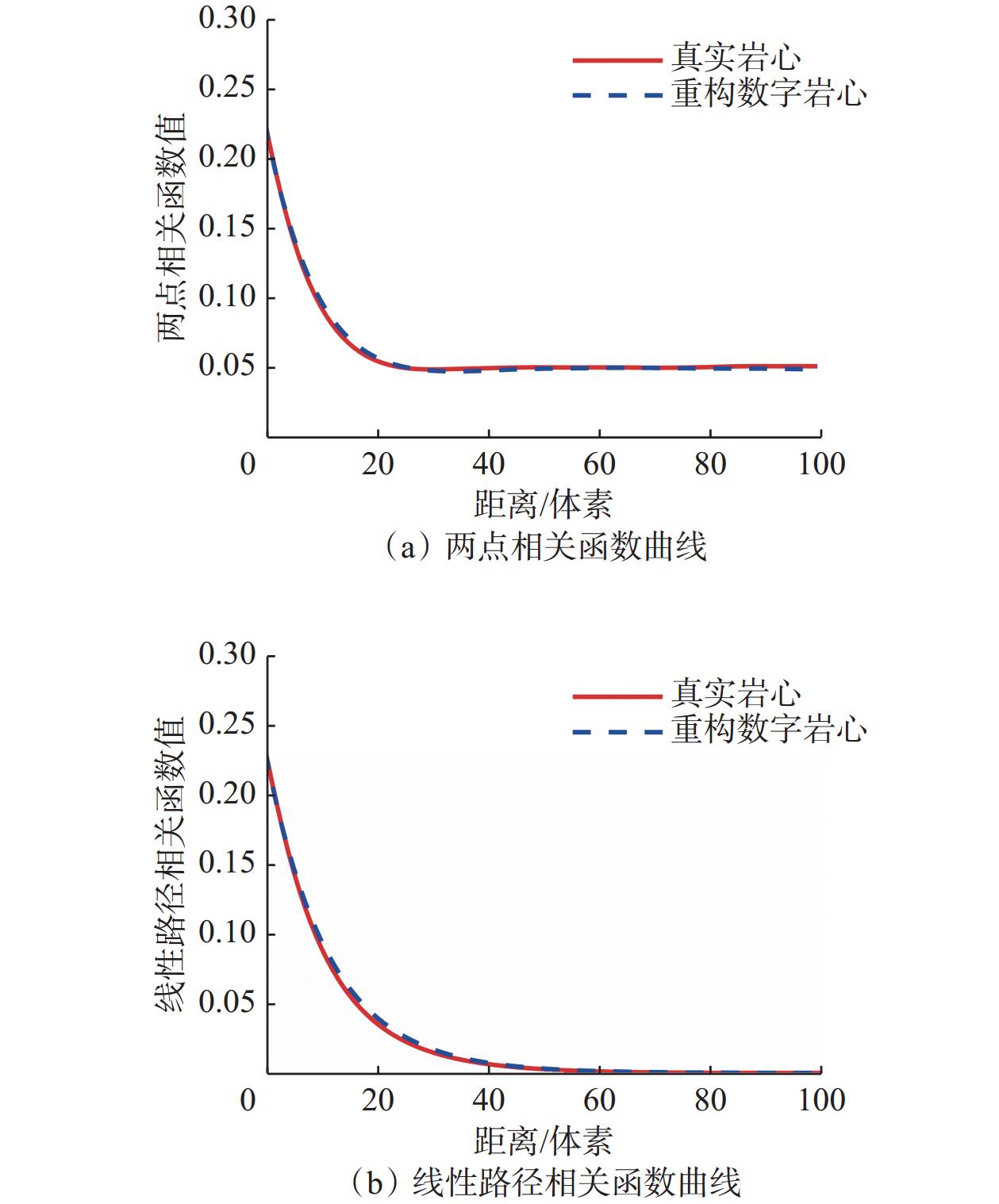
重构数字岩心REV内的两点相关函数（S2）和线性路径相关函数（L）曲线与真实岩心的对比结果如图7所示。
![]()
图 7 重构岩心与真实岩心的两点相关和线性路径相关函数曲线对比结果Figure 7. Comparison of two-point correlation and linear path correlation function curves between reconstructed and real cores从图7可以看出，距离r为0时，S2和L的数值为模型的孔隙度（重构数字岩心和真实岩心分别为22.88%和22.95%）；r趋近于无穷大时，S2接近于孔隙度的平方，L趋近于0。此外，重构数字岩心和真实岩心的2个相关函数曲线基本重合，表明重构的常温常压数字岩心离散元模型能够反映真实岩心的孔隙结构。
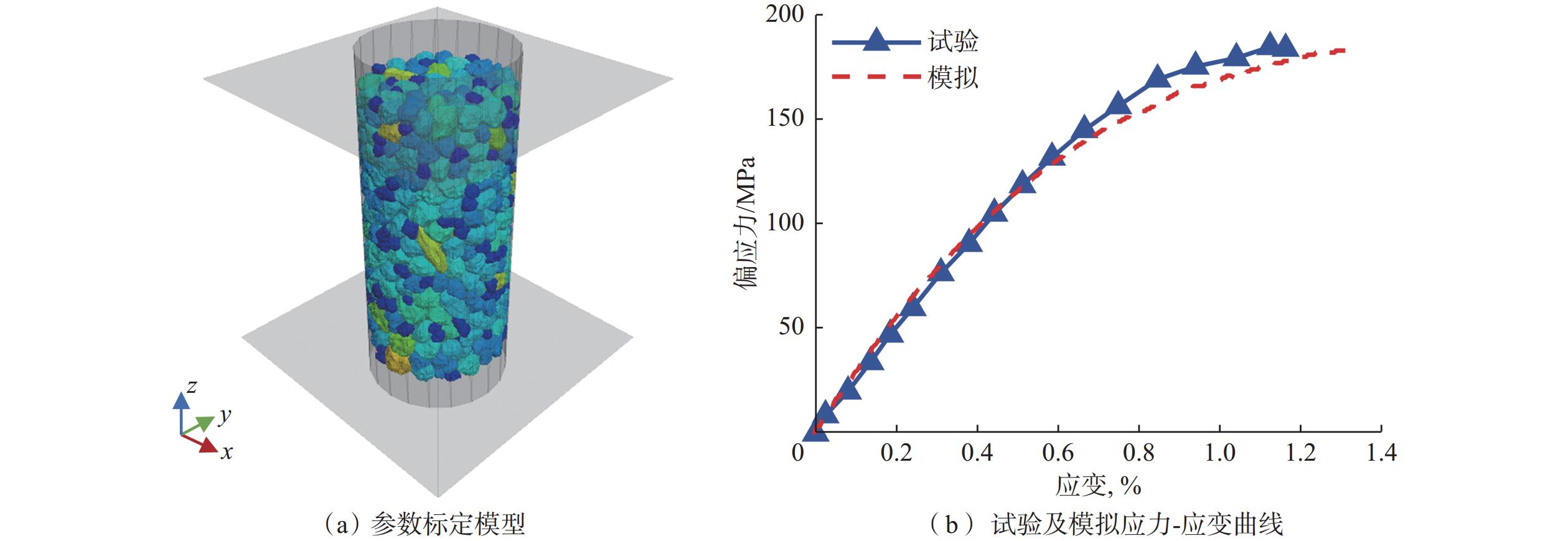
根据图3（a）的粒径分布曲线，将粒径等比例放大15倍，建立与力学试验相同尺寸（直径2 cm，高度4 cm）的离散元模型[32]，如图8（a）所示；通过调整平行黏结接触模型中的参数，使模拟得到的应力应变曲线与实际应力应变曲线相吻合，结果如图8（b）所示，此时模型的微观力学参数：有效模量和黏结模量为1.30 GPa，法向-切向刚度比和黏结法向-切向刚度比均为1.50，抗拉强度0.70 MPa，内聚力0.50 MPa，摩擦角55.0°。
![]()
图 8 颗粒间微观力学参数标定模型及偏应力-应变曲线Figure 8. Micromechanical parameter calibration model among particles and the deviational stress-strain curve3. 考虑应力作用的数字岩心构建与分析
首先，分别设置3种围压（50/70, 70/90和90/110 MPa）和轴向应力（120, 150和180 MPa），在PFC3D中设置不同应力组合模拟应力加载，得到受应力压实后的离散元模型；然后，使用体素化算法将离散元模型转化为数字岩心，采用最大球算法提取不同应力作用下数字岩心的孔隙网络，分析不同应力下数字岩心的孔隙度、孔隙半径、喉道半径、喉道长度和比欧拉示性数的变化，并计算了渗透率。
3.1 数字岩心构建结果
不同应力组合条件下的数字岩心构建结果如表1所示。从表1可以看出，围压相同的情况下，轴向应力越大，颗粒的位移量越大；轴向应力相同的情况下，颗粒的位移量会随围压增大而减小。颗粒的位移导致岩心孔隙几何拓扑结构的改变，最终造成不同应力下数字岩心孔隙度和渗透率的差异。
表 1 不同应力组合下的数字岩心构建结果Table 1. Digital core construction results under different stress combinationss水平应力 σz = 120 MPa σz = 150 MPa σz = 180 MPa σx = 50 MPa
σy = 70 MPa
σx = 70 MPa
σy = 90 MPa
σx = 90 MPa
σy = 110 MPa
3.2 数字岩心孔隙几何拓扑结构分析
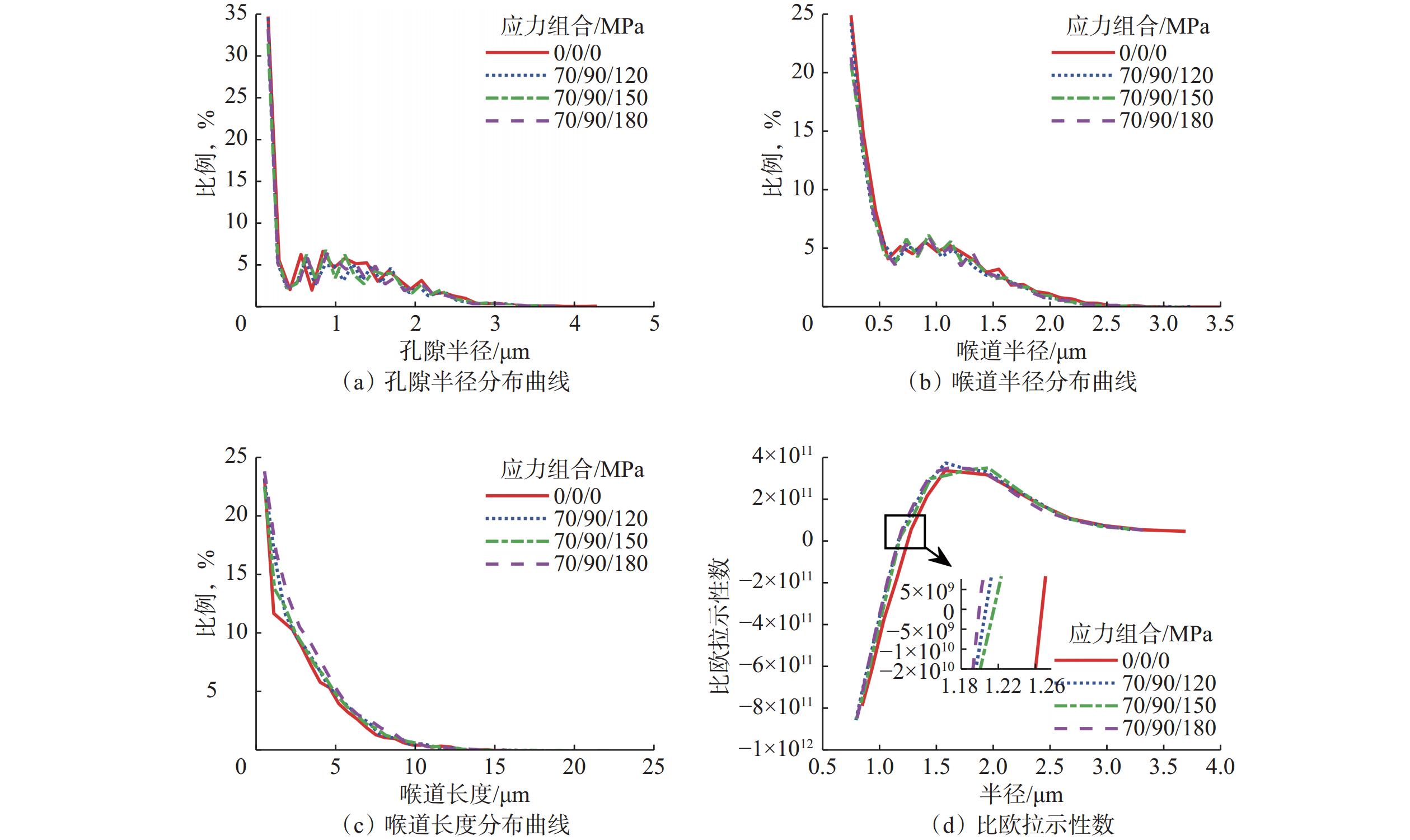
相同围压、不同轴向应力下的数字岩心孔隙几何拓扑结构如图9所示。图9（a）是围压σx = 70 MPa、σy = 90 MPa，轴向应力不同时的孔隙半径分布曲线，可以看出在应力作用下，孔隙半径的最大值由4.27 μm减小至3.70 μm；由于孔隙闭合，孔隙半径小于0.40 μm孔隙的比例略有减小；孔隙半径0.40～2.00 μm范围内分布情况剧烈波动。图9（b）为喉道半径分布曲线，随着轴向应力增大，喉道半径的最大值由3.41 μm减小至3.06 μm，小于0.50 μm和大于1.50 μm喉道的比例减小；0.50～1.50 μm范围内喉道的比例波动剧烈，但整体比例增大。图9（c）为喉道长度分布曲线，随着轴向应力增大，分布曲线整体右移，最大喉道长度由17.56 μm增大至21.88 μm。图9（d）为比欧拉示性数曲线，其与直线y = 0的交点值表征数字岩心连通性，其值越大，表示连通性越好；应力增大，曲线与直线y = 0交点值减小，表明岩心的连通性变差。
![]()
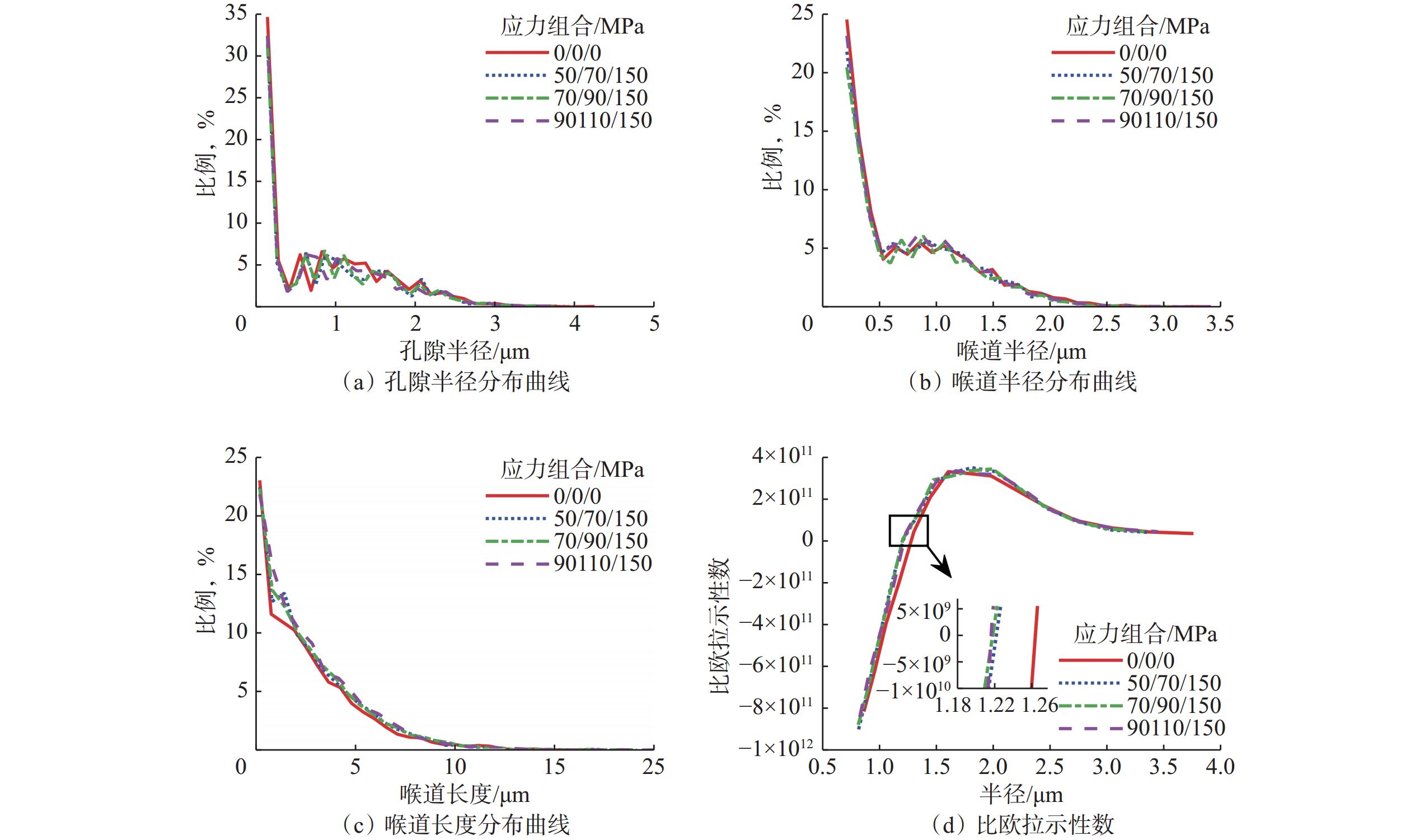
图 9 相同围压、不同轴压下的数字岩心孔隙几何拓扑结构Figure 9. Pore geometry topology of digital core under same confining pressure and different axial pressures相同轴向应力、不同围压下的数字岩心孔隙几何拓扑结构如图10所示。图10（a）和（b）分别为轴向应力为150 MPa时不同围压下数字岩心的孔隙半径分布曲线和喉道半径分布曲线，与常温常压数字岩心相比，应力的作用会造成孔隙半径和喉道半径的最大值减小，但是围压大的模型，减小幅度越小，能够保留更多的小半径孔隙和喉道。图10（c）为不同围压下数字岩心的喉道长度分布曲线，可以发现喉道长度分布曲线随围压增加向右移动，分布范围变大。图10（d）为不同围压下数字岩心比欧拉示性数曲线，其与直线y = 0交点值随围压增大而减小，表明数字岩心的连通性变差。
![]()
图 10 相同轴向应力、不同围压下的数字岩心孔隙几何拓扑结构Figure 10. Pore geometry topology of digital core under same axial stress and different confining pressures因此，改变围压和轴向应力，均会造成数字岩心孔隙半径喉道半径剧烈变化，其最大值减小，小于体素大小的孔隙和喉道闭合；喉道长度随着围压和轴向应力增大而增大，导致孔隙之间的传导距离变长，从而造成比欧拉示性数曲线与直线y = 0交点值变小，即数字岩心连通性变差。
3.3 不同应力数字岩心孔隙度和渗透率演化分析
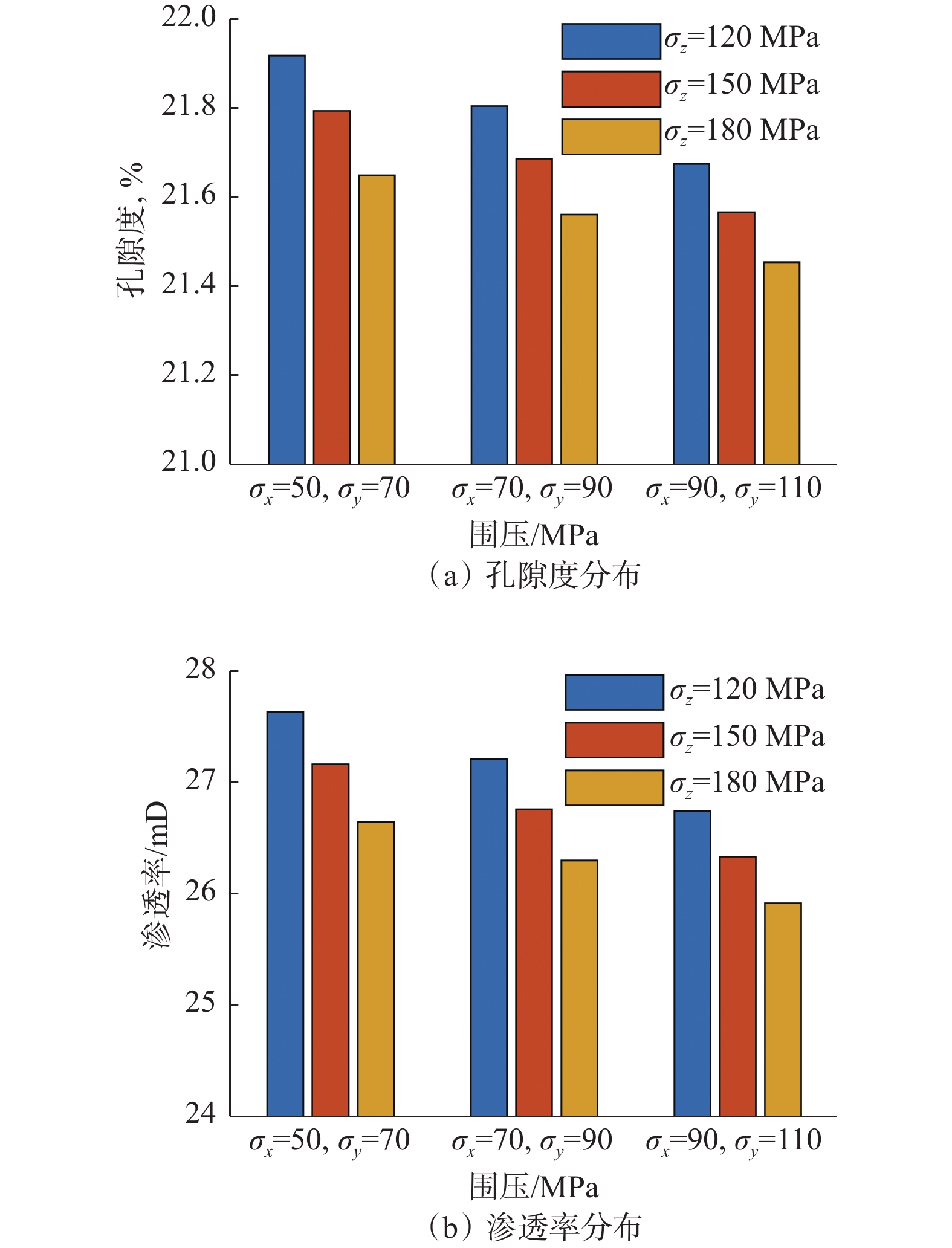
不同应力组合作用下数字岩心的孔隙度和渗透率柱状图如图11所示。从图11（a）可以看出，围压和轴向应力增大，均会造成孔隙度降低，最大降低幅度为6.21%；结合3.2节的孔隙和喉道尺寸分析结果，孔隙度降低的主要原因是应力作用下小于体素尺寸孔隙和喉道的闭合，以及大于体素尺寸孔隙和喉道半径的减小，导致孔隙和喉道的数量减少和小半径孔隙喉道的比例增加，最终造成数字岩心孔隙度降低。从图11（b）可以看出，围压和轴向应力增大，同样会导致数字岩心渗透率降低，常温常压下数字岩心模型的渗透率为31.50 mD，90/110/180 MPa应力组合作用下数字岩心的渗透率为25.96 mD，降幅为17.61%。
![]()
图 11 不同应力组合作用下数字岩心孔隙度和渗透率的分布Figure 11. Porosity and permeability distribution of digital core under different stress combinationsYang Yongfei等人[33]实验研究 表明，围压作用下岩石孔隙度的降低幅度为12.21%，渗透率的降低幅度为31.0%，即渗透率的应力敏感性远超孔隙度。模拟结果表明，孔隙度最大降幅为6.21%，渗透率为17.61%，符合渗透率应力敏感性大于孔隙度应力这一实验规律。Lu Jun等人[34]研究表明，真三轴应力下深部储层岩石的渗透率随应力增大的最大降幅（偏应力为60 MPa时）为18.57%，模拟结果为17.61%，相对误差为4.85%。本文模拟结果和文献中实验结果的对比表明，模拟结果能够很好地反映深部岩石物性在应力作用下的变化规律。
4. 结论与建议
1）基于离散元法，提出了一种考虑深层超深层油气藏高应力影响的数字岩心重构方法。该方法可以构建出任意应力下的数字岩心。离散元建模时，采用球面谐波分析方法，并考虑了颗粒的实际形状，提升了模型的准确性，构建的数字岩心更能反映实际岩石的孔隙结构。
2）以Bentheim砂岩为例，构建了不同应力作用下的数字岩心，孔隙几何拓扑结构分析表明，随着围压和轴向应力增大，颗粒向模型内部位移量增大，孔隙和喉道被压缩，喉道长度拉长，连通性变差，最终导致数字岩心的孔隙度和渗透率降低；对比文献中的实验结果，模拟结果能精确反映应力对孔隙度和渗透率的影响。
3）应用该方法重构数字岩心时，必须同时获取深部储层岩石在常温常压下的CT扫描图像和应力应变曲线，用于离散元建模与应力加载模拟，最终生成深层超深层油气藏的数字岩心。在这个过程中，岩心图像向颗粒的转化是关键步骤，对图像的分辨率要求极高。因此，建议继续研究更高效和普适的图像颗粒化方法。
-
![]()
图 2 常温常压数字岩心离散元建模流程
Figure 2. Flowchart of digital core modeling at normal temperature and pressure by DEM
![]()
图 3 样品粒径及颗粒形状分析结果
Figure 3. Analysis results of particle size and particle shapes of the sample
![]()
图 4 球面描述符与SH阶数的关系曲线
Figure 4. Relationship between the spherical descriptor and SH degree
![]()
图 5 常温常压数字岩心离散元建模结果
Figure 5. Results of digital core modeling at normal temperature and pressure by DEM
![]()
图 7 重构岩心与真实岩心的两点相关和线性路径相关函数曲线对比结果
Figure 7. Comparison of two-point correlation and linear path correlation function curves between reconstructed and real cores
![]()
图 8 颗粒间微观力学参数标定模型及偏应力-应变曲线
Figure 8. Micromechanical parameter calibration model among particles and the deviational stress-strain curve
![]()
图 9 相同围压、不同轴压下的数字岩心孔隙几何拓扑结构
Figure 9. Pore geometry topology of digital core under same confining pressure and different axial pressures
![]()
图 10 相同轴向应力、不同围压下的数字岩心孔隙几何拓扑结构
Figure 10. Pore geometry topology of digital core under same axial stress and different confining pressures
![]()
图 11 不同应力组合作用下数字岩心孔隙度和渗透率的分布
Figure 11. Porosity and permeability distribution of digital core under different stress combinations
表 1 不同应力组合下的数字岩心构建结果
Table 1 Digital core construction results under different stress combinationss
水平应力 σz = 120 MPa σz = 150 MPa σz = 180 MPa σx = 50 MPa
σy = 70 MPaσx = 70 MPa
σy = 90 MPaσx = 90 MPa
σy = 110 MPa
下载: 导出CSV
-
[1] 贾承造,庞雄奇. 深层油气地质理论研究进展与主要发展方向[J]. 石油学报,2015,36(12):1457–1469. JIA Chengzao, PANG Xiongqi. Research processes and main development directions of deep hydrocarbon geological theories[J]. Acta Petrolei Sinica., 2015, 36(12): 1457–1469.
[2] 范家伟,袁野,李绍华,等. 塔里木盆地深层致密油藏地质工程一体化模拟技术[J]. 断块油气田,2022,29(2):194–198. FAN Jiawei, YUAN Ye, LI Shaohua, et al. Geology-engineering integrated simulation technology of deep tight oil reservoir in Tarim Basin[J]. Fault-Block Oil & Gas Field, 2022, 29(2): 194–198.
[3] 陈建勋. 深层高压碳酸盐岩气藏孔隙结构特征及衰竭开发规律[J]. 特种油气藏,2022,29(5):80–87. CHEN Jianxun. Pore structure characteristics and natural depletion law of deep high-pressure carbonate gas reservoirs[J]. Special Oil & Gas Reservoirs, 2022, 29(5): 80–87.
[4] 曾义金. 中国石化深层超深层油气井固井技术新进展与发展建议[J]. 石油钻探技术,2023,51(4):66–73. ZENG Yijin. Novel advancements and development suggestions of cementing technologies for deep and ultra-deep wells of Sinopec[J]. Petroleum Drilling Techniques, 2023, 51(4): 66–73.
[5] 王建云,韩涛,赵宽心,等. 塔深5井超深层钻井关键技术[J]. 石油钻探技术,2022,50(5):27–33. WANG Jianyun, HAN Tao, ZHAO Kuanxin, et al. Key drilling technologies for the ultra-deep Well Tashen 5[J]. Petroleum Drilling Techniques, 2022, 50(5): 27–33.
[6] 李虹,于海洋,杨海烽,等. 裂缝性非均质致密储层自适应应力敏感性研究[J]. 石油钻探技术,2022,50(3):99–105. LI Hong, YU Haiyang, YANG Haifeng, et al. Adaptive stress sensitivity study of fractured heterogeneous tight reservoir[J]. Petroleum Drilling Techniques, 2022, 50(3): 99–105.
[7] 孙强,孙志刚,张超. DLH油田低渗砂岩孔隙分形定量表征方法研究[J]. 西南石油大学学报(自然科学版),2023,45(1):105–116. SUN Qiang, SUN Zhigang, ZHANG Chao. A study on fractal quantitative characterization method of low permeability sandstone pore in DLH Oilfield[J]. Joumal of Southwest Petroleum University (Seience & Technology Edition), 2023, 45(1): 105–116.
[8] 姚军,黄朝琴,刘文政,等. 深层油气藏开发中的关键力学问题[J]. 中国科学:物理学 力学 天文学,2018,48(4):044701. YAO Jun, HUANG Zhaoqin, LIU Wenzheng, et al. Key mechanical problems in the development of deep oil and gas reservoirs[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2018, 48(4): 044701.
[9] 李荣强,高莹,杨永飞,等. 基于CT扫描的岩心压敏效应实验研究[J]. 石油钻探技术,2015,43(5):37–43. LI, Rongqiang, GAO Ying, YANG Yongfei, et al. Experimental study on the pressure sensitive effects of cores based on CT scanning[J]. Petroleum Drilling Techniques, 2015, 43(5): 37–43.
[10] 王晨晨,姚军,杨永飞,等. 基于CT扫描法构建数字岩心的分辨率选取研究[J]. 科学技术与工程,2013,13(4):1049–1052. WANG Chenchen, YAO Jun, YANG Yongfei, et al. Study on resolution selection for digital rock construction with CT scanning method[J]. Science Technology and Engineering, 2013, 13(4): 1049–1052.
[11] 刘洋,王春生,孙启冀,等. 低渗砂岩储层数字岩心构建及渗流模拟[J]. 断块油气田,2017,24(6):817–821. LIU Yang, WANG Chunsheng, SUN Qiji, et al. Digital core construction and seepage simulation of low permeability sandstone reservoir[J]. Fault-Block Oil & Gas Field, 2017, 24(6): 817–821.
[12] 姚军,宋文辉,李阳,等. 有机质孔隙对页岩气流动能力影响研究[J]. 中国科学:物理学 力学 天文学,2017,47(9):094702. doi: 10.1360/SSPMA2017-00040 YAO Jun, SONG Wenhui, LI Yang, et al. Study on the influence of organic pores on shale gas flow ability[J]. Scientia Sinaca: Physica, Mechanica & Astronomica, 2017, 47(9): 094702. doi: 10.1360/SSPMA2017-00040
[13] ØREN P E, BAKKE S. Process based reconstruction of sandstones and prediction of transport properties[J]. Transport in Porous Media, 2002, 46(2): 311–343.
[14] 姚军,赵秀才,衣艳静,等. 数字岩心技术现状及展望[J]. 油气地质与采收率,2005,12(6):52–54. YAO Jun, ZHAO Xiucai, YI Yanjing, et al. The current situation and prospect on digital core technology[J]. Petroleum Geology and Recovery Efficiency, 2005, 12(6): 52–54.
[15] YANG Yongfei, LIU Fugui, YAO Jun, et al. Multi-scale reconstruction of porous media from low-resolution core images using conditional generative adversarial networks[J]. Journal of Natural Gas Science and Engineering, 2022, 99: 104411. doi: 10.1016/j.jngse.2022.104411
[16] 杨永飞,刘夫贵,姚军,等. 基于生成对抗网络的页岩三维数字岩芯构建[J]. 西南石油大学学报(自然科学版),2021,43(5):73–83. YANG Yongfei, LIU Fugui, YAO Jun, et al. Reconstruction of 3D shale digital rock based on generative adversarial network[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2021, 43(5): 73–83.
[17] 陈林,黎棚武,张绍俊,等. 基于机器学习的岩芯渗透率及裂缝开度预测[J]. 西南石油大学学报(自然科学版),2023,45(4):155–163. CHEN Lin, LI Pengwu, ZHANG Shaojun, et al. Prediction method of core permeability and fracture aperture based on machine learning[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2023, 45(4): 155–163.
[18] SAENGER E H, LEBEDEV M, URIBE D, et al. Analysis of high-resolution X-ray computed tomography images of Bentheim sandstone under elevated confining pressures[J]. Geophysical Prospecting, 2016, 64(4): 848–859.
[19] ZHU Linqi, ZHANG Chong, ZHANG Chaomo, et al. Challenges and prospects of digital core-reconstruction researc[J]. Geofluids, 2019, 2019: 7814180.
[20] FAN Ming, MCCLURE J, HAN Yanhui, et al. Interaction between proppant compaction and single-/multiphase flows in a hydraulic fracture[J]. SPE Journal, 2018, 23(4): 1290–1303. doi: 10.2118/189985-PA
[21] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47–65. doi: 10.1680/geot.1979.29.1.47
[22] ZHENG Junxing, HRYCIW R D. Segmentation of contacting soil particles in images by modified watershed analysis[J]. Computers and Geotechnics, 2016, 73: 142–152. doi: 10.1016/j.compgeo.2015.11.025
[23] ZHAO Shiwei, ZHAO Jidong. A poly-superellipsoid-based approach on particle morphology for DEM modeling of granular media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(13): 2147–2169.
[24] ANDRADE J E, LIM K W, AVILA C F, et al. Granular element method for computational particle mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 241(): 262–274.
[25] BOWMAN E T, SOGA K, DRUMMOND W. Particle shape characterisation using Fourier descriptor analysis[J]. Geotechnique, 2001, 51(6): 545–554.
[26] GARBOCZI E J. Three-dimensional mathematical analysis of particle shape using X-ray tomography and spherical harmonics: application to aggregates used in concrete[J]. Cement and concrete research, 2002, 32(10): 1621–1638.
[27] WEI Deheng, WANG Jianfeng, ZHAO Budi. A simple method for particle shape generation with spherical harmonics[J]. Powder Technology, 2018, 330: 284–291. doi: 10.1016/j.powtec.2018.02.006
[28] LI Zechuang, LIU Zhibin. Influence of particle shape on the macroscopic and mesolevel mechanical properties of slip zone soil based on 3D scanning and 3D DEM[J]. Advances in Materials Science and Engineering, 2021, 2021: 1–14.
[29] LAI Zhengshou, CHEN Qiushi. Characterization and discrete element simulation of grading and shape-dependent behavior of JSC-1A Martian regolith simulant[J]. Granular Matter, 2017, 19(4): 69.
[30] KHALEGHI K, TALMAN S, SHOKRI A R, et al. A coupled pore-scale modelling approach to capture macro-scale stress-dependent permeability of rocks[R]. URTEC 198264, 2019.
[31] KAWAMOTO R, ANDÒ E, VIGGIANI G, et al. Level set discrete element method for three-dimensional computations with triaxial case study[J]. Journal of the Mechanics and Physics of Solids, 2016, 91: 1–13.
[32] KLEIN E, BAUD P, REUSCHLÉ T et al. Mechanical behaviour and failure mode of bentheim sandstone under triaxial compression[J]. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, 2001, 26(1/2): 21–25.
[33] YANG Yongfei, ZHANG Wenjie, GAO Ying, et al. Influence of stress sensitivity on microscopic pore structure and fluid flow in porous media[J]. Journal of Natural Gas Science and Engineering, 2016, 36(part A): 20–31.
[34] LU Jun, YIN Guangzhi, DENG Bozhi, et al. Permeability characteristics of layered composite coal-rock under true triaxial stress conditions[J]. Journal of Natural Gas Science and Engineering, 2019, 66: 60–76. doi: 10.1016/j.jngse.2019.03.023
-
期刊类型引用(9)
1. 伍藏原，张迅，李杨，姚杰，冯其红. 塔中深层稠油减氧空气驱氧化特征及机理研究. 西南石油大学学报(自然科学版). 2024(04): 131-137 . 
百度学术
2. 佘治成，陈利新，徐三峰，肖云，张键. 缝洞型碳酸盐岩油藏注氮气提高采收率技术. 西南石油大学学报(自然科学版). 2024(04): 138-148 . 百度学术
3. 王林，岳鹏，安高诧. 塔河油田油田水除氧剂的筛选与应用. 内蒙古石油化工. 2024(10): 36-39 . 百度学术
4. 牟汉生，陆文明，曹长霄，宋兆杰，石军太，张洪. 深水浊积岩油藏提高采收率方法研究——以安哥拉X油藏为例. 石油钻探技术. 2021(02): 79-89 . 本站查看
5. 刘中云，李兆敏，赵海洋. 缝洞型碳酸盐岩油藏注氮气致稠机理研究. 石油钻探技术. 2021(05): 75-80 . 本站查看
6. 李海波，李永会，姜瑜，陈凤，吕世瑶，展宏洋. 多层砂砾岩油藏注烟道气提高采收率技术. 断块油气田. 2020(01): 104-108 . 百度学术
7. 张伟，海刚，张莹. 塔河油田碳酸盐岩缝洞型油藏气水复合驱技术. 石油钻探技术. 2020(01): 61-65 . 本站查看
8. 贾国振. 略谈油田氮气开采技术的运用. 化工管理. 2020(07): 57-58 . 百度学术
9. 李二党，韩作为，高祥瑞，马明宇，邱钧超. 不同注气介质驱替致密油藏微观孔隙动用特征研究. 石油钻探技术. 2020(05): 85-91 . 本站查看
其他类型引用(1)
计量
- 文章访问数: 238
- HTML全文浏览量: 50
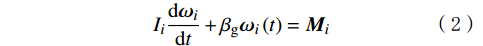
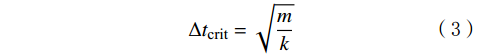
- PDF下载量: 113
- 被引次数: 10
