Rock Breaking Process and Efficiency Analysis of Conical Cutting Teeth under Rotary and Torsional Impact
-
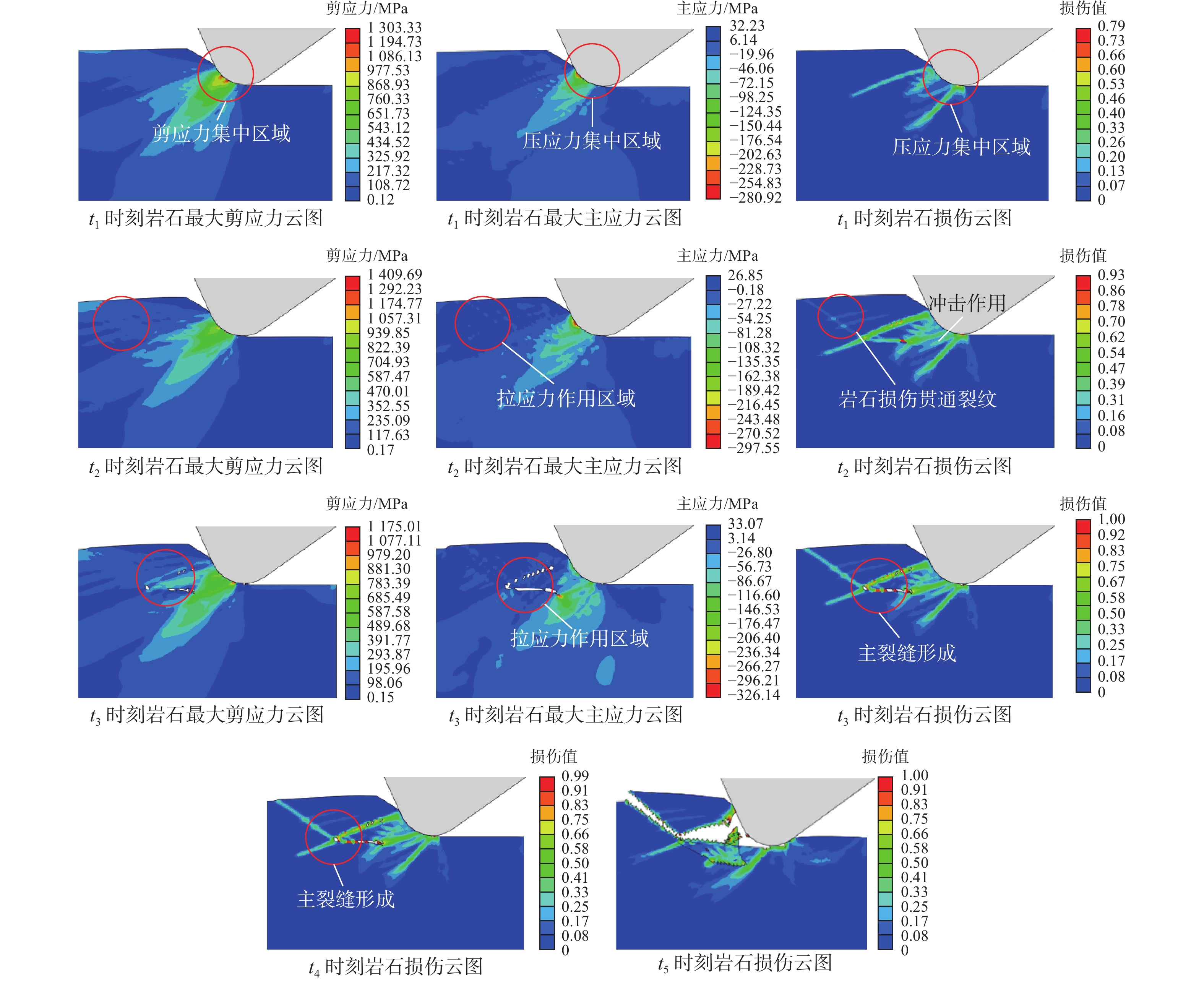
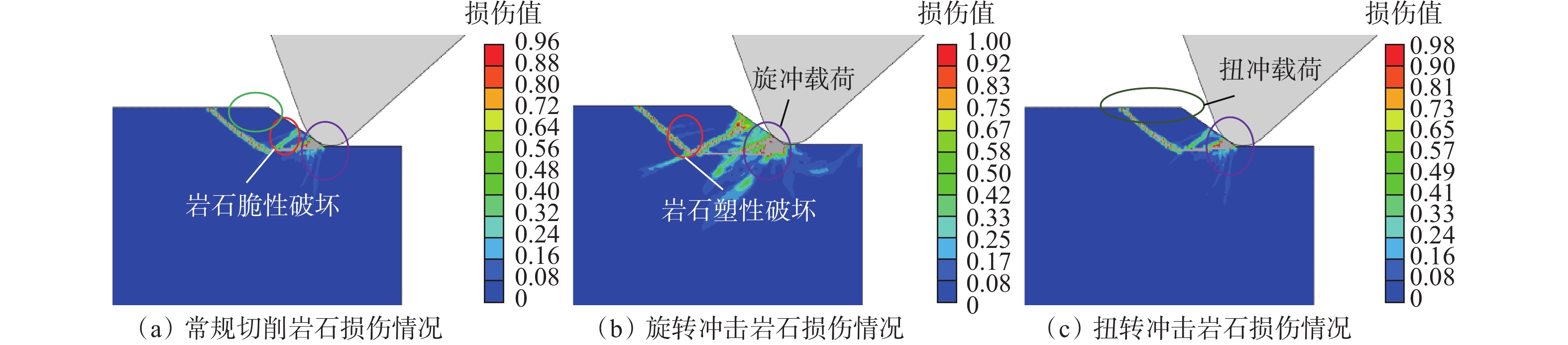
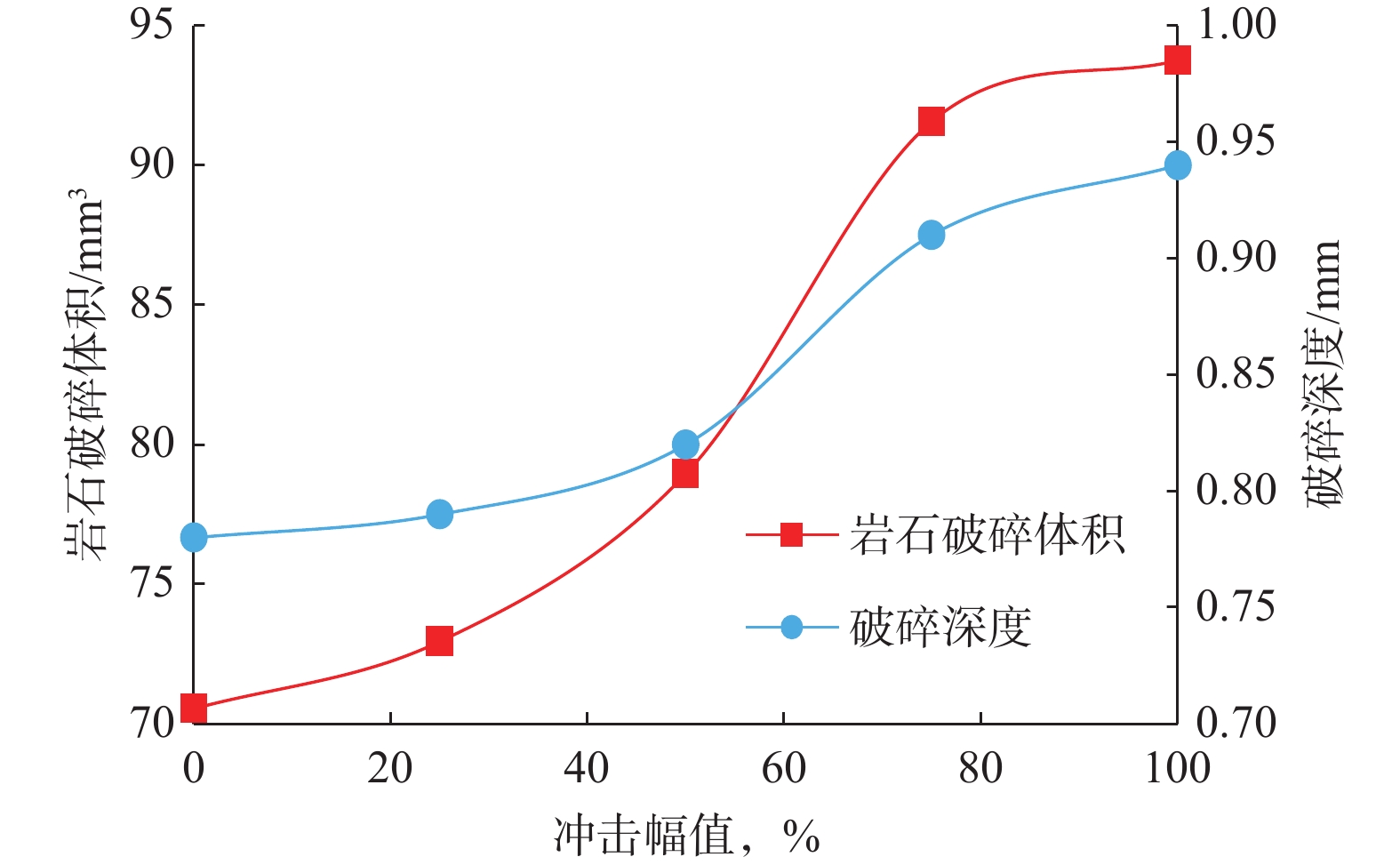
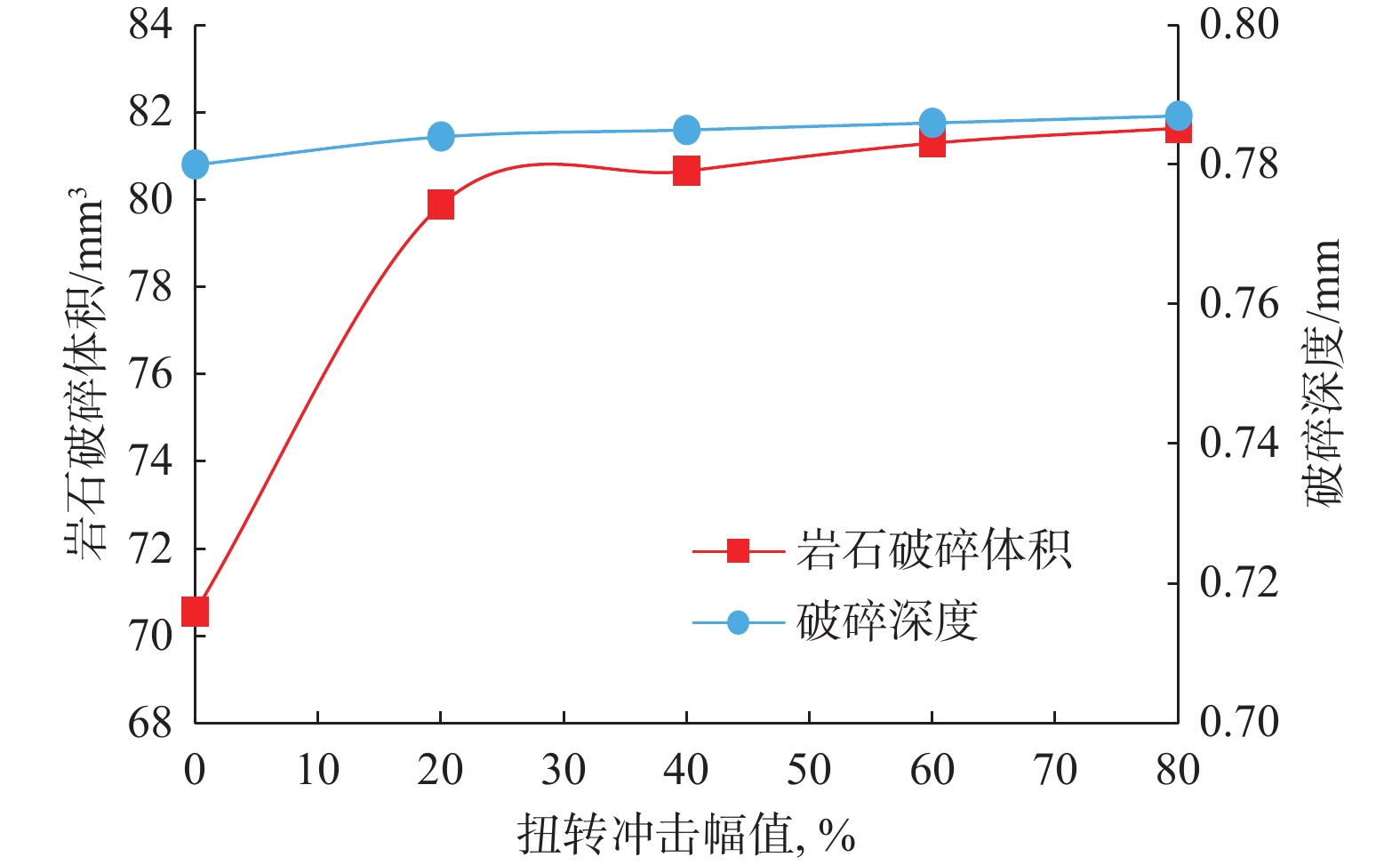
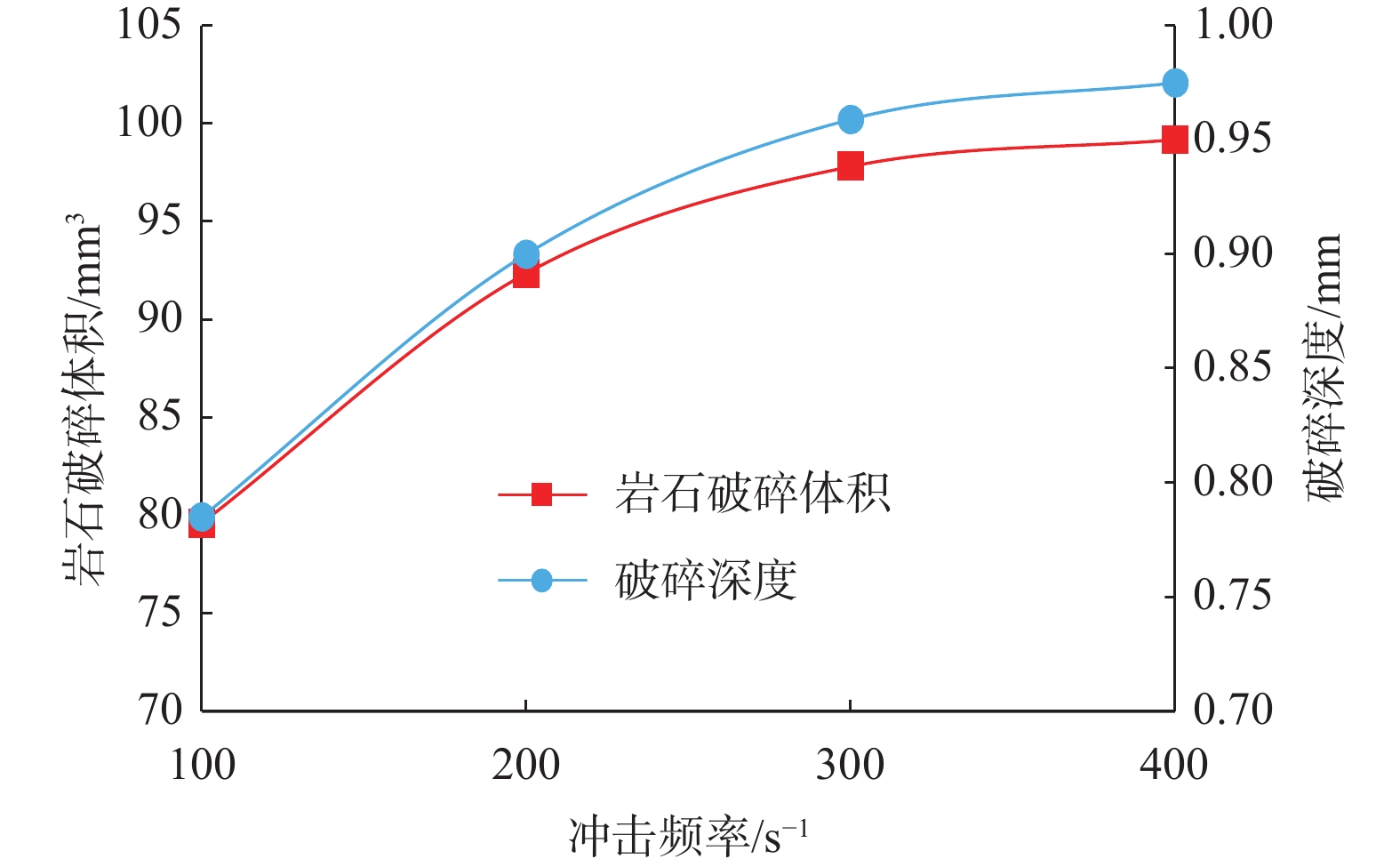
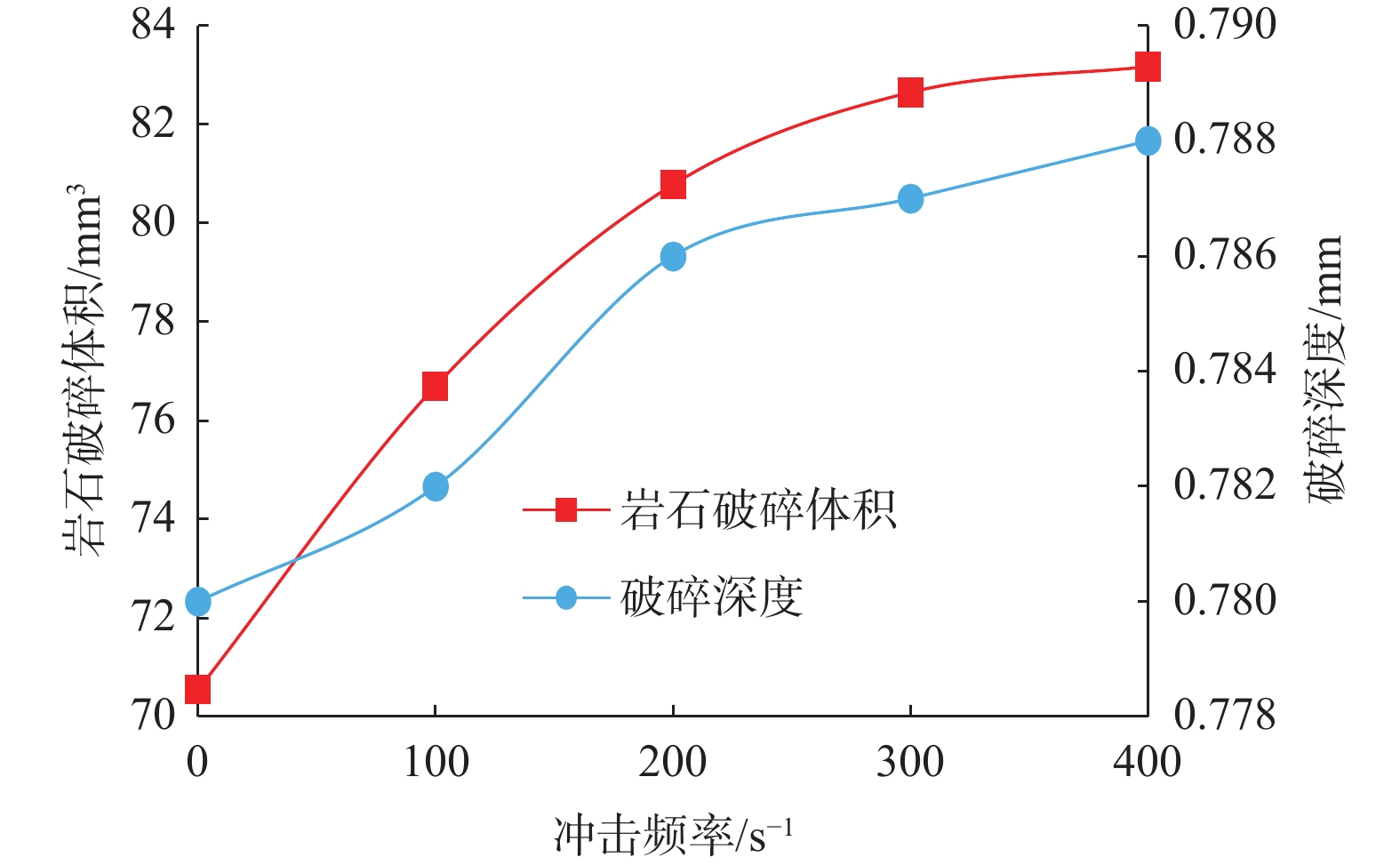
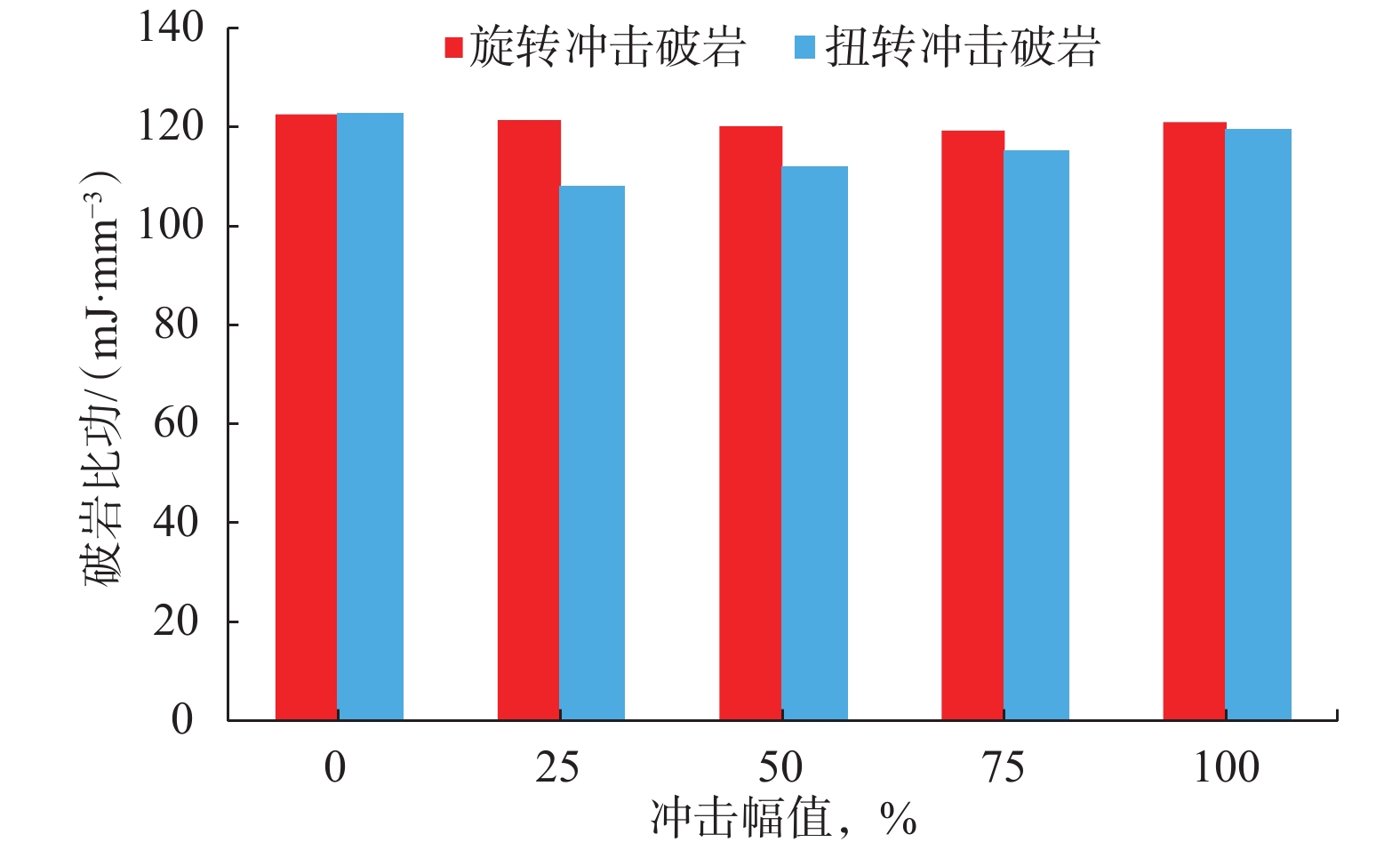
摘要: 为了解锥形齿在旋转冲击和扭转冲击载荷作用下的破岩过程和破岩效率，采用数值模拟和试验数据验证的方法，研究了2种破岩方式下不同冲击幅值和冲击频率对应的岩石内部应力变化、岩石损伤特征、岩石破碎体积和破碎深度、破岩比功。数值模拟分析结果表明，锥形齿在旋转冲击和扭转冲击破岩过程中均表现为切削齿侵入岩石、岩石损伤贯通裂纹萌生、岩石损伤贯通裂纹扩展、裂缝贯通岩屑崩落4个阶段，拉应力是引起岩石内部到表面贯通裂缝产生的主要原因，压剪应力是岩石内部出现损伤和形成微裂纹的主要原因。随着冲击幅值和冲击频率增大，旋转冲击和扭转冲击破岩方式下，锥形齿破碎岩石的体积都会增大，但当冲击幅值和冲击频率增加到一定值时，岩石破碎体积的增加趋势趋于平缓；锥形齿旋转冲击破岩方式下的最大破碎体积高于扭转冲击破岩方式。常规切削、旋转冲击和扭转冲击3种破岩方式下，锥形齿常规切削的破岩比功最大，不同冲击幅值和冲击频率条件下，锥形齿扭转冲击破岩方式下的破岩比功普遍比旋转冲击破岩方式低。Abstract: In order to gain a better understanding of the rock-breaking process and efficiency of conical cutting teeth under rotary and torsional impact loads, numerical simulation and experimental data verification were conducted to study the rock’s internal stress changes, damage characteristics, breaking volume, depth and rock breaking specific work by the two methods at different impact amplitudes and frequencies. The numerical simulation and analysis results showed that both the rock-breaking processes of conical cutters under rotary impact and torsional impact could be divided into four stages: cutter intruding into rock, damage through crack initiation, damage through crack propagation, and rock cuttings avalanche. The tensile stress is the main reason for the cracks from the inside to the surface of rock, and the internal damage and micro-cracks appear mainly due to compressive shear stress. With the increase of impact amplitude and impact frequency, the broken volume of rock will increase in both the two ways. When the impact amplitude and frequency are increased to certain values, the increase of rock-breaking volume tends to be mild, and the maximum rock-breaking volume under rotary impact is higher than that under torsional impact. Among the three rock breaking methods - conventional cutting, rotary impact and torsional impact - the rock breaking specific work of conventional cutting is the greatest, and the rock breaking specific work under the conditions of different impact amplitudes and frequency of torsional impact is generally lower than that of rotary impact.
-
现代地质导向钻井过程中，需采用近钻头随钻边界探测技术动态测量近钻头井眼轨迹参数（井斜角、方位角和工具面角），根据随钻成像预估地层和井眼变化趋势，据此调整钻头方向，提高油层钻遇率。由于振动、旋转、磁干扰等因素的影响，导致测量的近钻头井眼轨迹参数出现很大误差，严重影响了随钻测量精度，出现钻穿油层等情况。
目前旋转导向动态测量技术都掌握在国外油田技术服务公司手中，不对外公开，因此，未见到国外有井眼轨迹参数动态测量技术的报道。国内杨全进等人[1]建立了一种旋转导向系统有色噪声的改进无迹卡尔曼滤波方法，该算法限制条件较多。高怡等人[2]提出了采用多源动态姿态组合测量方法测量导向钻具的动态姿态，但加速度计采集数据的存储周期较长，造成测量误差较大。Xue Qilong等人[3-4]提出了基于卡尔曼滤波状态空间模型的动态井眼轨迹测量方法，但其只适用于线性系统。徐宝昌等人[5]提出了基于无迹卡尔曼滤波的动态姿态测量方法，但没有解决振动及旋转对动态姿态测量的影响。为此，笔者提出了一种基于数据融合的近钻头井眼轨迹参数动态测量方法，该方法针对三轴加速度计、磁通门和速率陀螺的测量系统，建立了基于四元数井眼轨迹参数测量模型，推导出加速度计与井眼轨迹平滑预测的关系，运用3个捷联式无迹卡尔曼滤波器和磁干扰校正系对加速度计、磁通门进行消噪，校正，实时测量近钻头井眼轨迹参数，提高随钻近钻头探边能力，确定最佳储层位置。
1. 近钻头动态井眼轨迹测量模型
近钻头动态测量系统由三轴加速度计、三轴磁通门和角速率陀螺仪组成，针对该系统，基于四元数方法建立井眼轨迹非线性数学模型。如图1所示，根据地理坐标系O-NED和钻具坐标系O-xyz的对应关系，建立欧拉角转换矩阵，并转换为四元数，k时刻姿态转换矩阵T表示为：
{\boldsymbol{T}}\left( k \right){{ = }} \left[ \begin{array}{l} {q_{\text{0}}^{\text{2}} + q_{\text{1}}^{\text{2}} - q_{\text{2}}^{\text{2}} - q_{\text{3}}^{\text{2}}}\\ {{\text{2}}\left( {{q_{\text{1}}}{q_{\text{2}}} + {q_{\text{0}}}{q_{\text{3}}}} \right)}\\ {{\text{2}}\left( {{q_{\text{1}}}{q_{\text{3}}} - {q_{\text{0}}}{q_{\text{2}}}} \right)}\end{array} \begin{array}{l} {{\text{2}}\left( {{q_{\text{1}}}{q_{\text{2}}} - {q_{\text{0}}}{q_{\text{3}}}} \right)}\\ {q_{\text{0}}^{\text{2}} - q_{\text{1}}^{\text{2}} + q_{\text{2}}^{\text{2}} - q_{\text{3}}^{\text{2}}}\\ {{\text{2}}\left( {{q_{\text{2}}}{q_{\text{3}}} + {q_{\text{1}}}{q_{\text{0}}}} \right)}\end{array} \begin{array}{l} {{\text{2}}\left( {{q_{\text{1}}}{q_{\text{3}}} + {q_{\text{0}}}{q_{\text{2}}}} \right)} \\ {{\text{2}}\left( {{q_{\text{2}}}{q_{\text{3}}} - {q_{\text{0}}}{q_{\text{1}}}} \right)} \\ {q_{\text{0}}^{\text{2}} - q_{\text{1}}^{\text{2}} - q_{\text{2}}^{\text{2}} + q_{\text{3}}^{\text{2}}} \end{array} \right] (1) 式中：q0，q1，q2和 q3为四元数。
理论上由于x轴和y轴的加速度计、磁通门正交相隔90°，其信号为正弦或余弦曲线。由于钻头旋转、振动的干扰，近钻头x轴和y轴加速度计、磁通门的实测信号如图2所示。由图2可以看出，近钻头的旋转、振动对磁通门的影响相对于加速度计较小，所以采取磁通门读数校正加速度计读数。
\frac{{{B_x}(k + 1)}}{{{B_x}(k)}} = \frac{{{a_x}(k + 1)}}{{{a_x}(k)}} = \frac{{B\sin ({w_x}(k + 1))}}{{B\sin ({w_x}(k))}} = \frac{{g\sin ({w_x}(k + 1))}}{{g\sin ({w_x}(k + 1))}} (2) \frac{{B\sin ({w_y}(k + 1))}}{{B\sin ({w_y}(k))}} = \frac{{g\sin ({w_y}(k + 1))}}{{g\sin ({w_y}(k + 1))}} = \frac{{{B_y}(k + 1)}}{{{B_y}(k)}} = \frac{{{a_y}(k + 1)}}{{{a_y}(k)}} (3) \left[ \begin{gathered} {a_x}(k + 1) \hfill \\ {a_y}(k + 1) \hfill \end{gathered}\right] = \left[ \begin{gathered} \frac{{{B_x}(k + 1)}}{{{B_x}(k)}} \hfill \\ 0 \hfill \\ \end{gathered} \begin{gathered} 0 \hfill \\ \frac{{{B_y}(k + 1)}}{{{B_y}(k)}} \hfill \\ \end{gathered}\right] \left[ \begin{gathered} {a_x}(k) \hfill \\ {a_y}(k) \hfill \\ \end{gathered}\right] (4) 式中：g为重力加速度，m/s2；B为地磁场强度，μT；Bx
\left(k\right) ，By\left(k\right) 和Bz\left(k\right) 为k时刻三轴磁通门测量的磁场强度，μT；ax\left(k\right) ，ay\left(k\right) 和az\left(k\right) 为k时刻三轴加速度计测量结果，m/s2；wx\left(k\right) ，wy\left(k\right) 和wz\left(k\right) 为k时刻陀螺仪的角速度，rad/s。2. 数据融合近钻头井眼轨迹参数动态测量方法
基于数据融合算法的近钻头井眼轨迹参数动态测量方法的测量流程如图3所示，图中KF1和KF2为基于扩展卡尔曼滤波算法的滤波器，KF3为基于无迹卡尔曼滤波算法的滤波器。测量步骤：1）将加速度计、磁通门、转动角速度四元数带入KF1滤波器，进行扩展卡尔曼滤波，得出井斜角、方位角估计值；2）将加速度计四元数带入KF2滤波器，进行扩展卡尔曼滤波，得出测深增量Δhm；3）将测深增量Δhm、井斜角、方位角估计值带入KF3滤波器，进行无迹卡尔曼滤波，得出井斜角、方位角最终估计值；4）利用井斜角、方位角最终估计值计算磁性工具面角ωm与重力工具面角的差Δω；5）利用磁性工具面角和角差Δω求出重力工具面角ωg。
近钻头振动信号是一种幅值大、频率高、频带宽的噪声信号，可以近似等效为高斯白噪声。动态测量的动力学模型为典型的非线性模型。根据z轴陀螺仪测量的转速wz，运用转速补偿策略，对x轴和y轴加速度计测量结果进行转速补偿[5]，减小钻具旋转对加速度计测量结果的影响。根据转速补偿结果以及噪声特性，采用扩展、无迹卡尔曼滤波滤除振动干扰信号。
2.1 估计近钻头井斜角、方位角的扩展卡尔曼滤波算法
基于四元数的KF1的状态方程和量测方程：
Q(k + 1) = ({\boldsymbol{I}}{\text{ + }}{t_{\text{s}}}{\boldsymbol{A}}(k))Q(k) + w(k) (5) Z(k + 1) = F(Q(k)) + v(k) (6) 式中：Q(k)为k时刻的状态值；I为单位矩阵；ts为采样周期；w(k)为k时刻系统高斯白噪声；v(k)为k时刻传感器观测噪声；A(k)为k时刻状态转移矩阵；F(x)为非线性函数；Z(k+1)为k+1时刻的观测值。
Z(k + 1) = \left[ \begin{gathered} {B_x} \hfill \\ {B_y} \hfill \\ {B_z} \hfill \\ {a_x} \hfill \\ {a_y} \hfill \\ {a_z} \hfill \\ \end{gathered} \right] = \left[ \begin{array}{l} T(k) \left[ \begin{array}{c} B\cos \theta \hfill \\ 0 \hfill \\ B\sin \theta \hfill \end{array} \right]\\ T(k) \left[\begin{gathered} 0 \hfill \\ 0 \hfill \\ g \hfill \\ \end{gathered} \right] \end{array}\right] + v(k) (7) \begin{split} & Q(k + 1) = \left(I + {t_{\text{s}}} \left[ \begin{array}{c} 0 \hfill \\ {w_x}(k) \hfill \\ {w_y}(k) \hfill \\ {w_z}(k) \hfill \\ \end{array} \begin{array}{c} - {w_x}(k) \hfill \\ 0 \hfill \\ - {w_z}(k) \hfill \\ {w_y}(k) \hfill \\ \end{array} \begin{array}{c} - {w_y}(k) \hfill \\ {w_z}(k) \hfill \\ 0 \hfill \\ - {w_x}(k) \hfill \\ \end{array} \begin{array}{c} - {w_z}(k) \hfill \\ - {w_y}(k) \hfill \\ {w_x}(k) \hfill \\ 0 \hfill \\ \end{array} \right] \right) \cdot \\ & \qquad\qquad Q(k) + w(k)\end{split} (8) 三轴加速度信号、三轴磁通门信号、角速率陀螺信号进行数据融合后，采用扩展卡尔曼滤波算法，得到最优姿态估计[6-7]，动态解算出钻井工具的实时姿态参数，确保钻具姿态测量计算的精度，减少计算量，对四元数Q进行更新，求出KF1滤波后的井斜角αKF1、方位角ϕKF1、高边工具面角ωg,KF1和磁性工具面角ωm,KF1。
{\alpha _{{\text{KF}}1}}{\text{ = }}\arctan \frac{{2({q_0}{q_1} + {q_2}{q_3})}}{{1 - 2(q_1^2 + q_2^2)}} (9) {\phi _{{\text{KF}}1}}{\text{ = }}\arctan \frac{{2({q_0}{q_3} + {q_1}{q_2})}}{{1 - 2(q_0^2 + q_3^2)}} (10) {\omega _{{\text{g}},{\text{KF}}1}}{\text{ = }}\arctan \frac{{({q_0}{q_2} + {q_1}{q_3})}}{{({q_0}{q_1} - {q_2}{q_3})}} (11) {\omega _{{\text{m}},{\text{KF}}1}}{{ = }}\arctan \frac{{({q_1}{q_2} + {q_0}{q_3})\cos \theta + ({q_1}{q_2} + {q_0}{q_3})\sin \theta }}{{(q_0^2 - q_1^2 - q_2^2 + q_3^2)\cos \theta + ({q_1}{q_3} - {q_0}{q_2})\sin \theta }} (12) 式中：αKF1，ϕKF1，ωg,KF1和ωm,KF1分别为KF1滤波后的井斜角、方位角、重力工具面角和磁性工具面角，（°）；θ为地层倾角，（°）。
2.2 估计近钻头测深增量的扩展卡尔曼滤波算法
根据式（7）计算出四元数中的az，运用扩展卡尔曼滤波器计算系统经过ts后测深增量Δhm。z轴加速度计主要受到重力加速度和振动的干扰，由于采样时间ts为毫秒级，在单位采样周期内，重力加速度和振动的干扰可以视为近似相同[8-10]，可以忽略振动对加速度计测量结果的影响。k为当前采样点，z轴加速度增量Δaz：
\Delta {a_z} = {a_z}(k + 1) - g\cos ({\alpha _{{\text{KF1}}}}(k)) (13) \Delta {a_z} = \Delta h_{\text{m}}^{''} (14) 为了提高对测深增量的估计，对Δhm进行二阶泰勒展开：
\Delta {h_{\text{m}}}(k + 1) = \Delta {h_{\text{m}}}(k) + \Delta {h_{\text{m}}}{(k)^{'}}{t_{\text{s}}} + 0.5\Delta {h_{\text{m}}}{(k)^{''}}t_{\text{s}}^{\text{2}} (15) KF2的状态方程和量测方程为：
\left[ \begin{gathered} \Delta {h_{\text{m}}}(k + 1) \\ \Delta {h_{\text{m}}}{(k + 1)^{'}} \\ \Delta {h_{\text{m}}}{(k + 1)^{''}} \\ \end{gathered} \right] = \left[ \begin{gathered} 1 \;\; {t_{\rm{s}}} \;\; t_{\rm{s}}^2 \hfill \\ 0 \;\;1 \;\;0 \hfill \\ 0\;\; 0 \;\;1 \hfill \end{gathered}\right] \left[ \begin{gathered} \Delta {h_{\text{m}}}(k) \\ \Delta {h_{\text{m}}}{(k)^{'}} \\ \Delta {h_{\text{m}}}{(k)^{''}} \\ \end{gathered} \right] + w(k) (16) \Delta {a_z} = \left[0 \; 0 \; 1\right] \left[ \begin{gathered} \Delta {h_{\text{m}}}(k + 1) \hfill \\ \Delta {h_{\text{m}}}{(k + 1)^{'}} \hfill \\ \Delta {h_{\text{m}}}{(k + 1)^{''}} \hfill \\ \end{gathered} \right] + v(k) (17) 2.3 估计近钻头井眼轨迹参数的无迹卡尔曼滤波算法
如图4所示，在单位采样时间内，井眼轨迹趋于平滑曲线，可以根据前面2个测点的狗腿度和KF2输出测深增量对井眼轨迹进行递归式预测[11]。
{h_{\text{m}}}(k + 1) = {h_{\text{m}}}(k) + \Delta {h_{\text{m}}}(k + 1) (18) \begin{split} & \;\;\;\;\;\;\; \gamma = \arccos \left[ {\cos \alpha (k)\cos \alpha (k - 1) + }\right. \\ & \left.{ \sin \alpha (k)\sin \alpha (k - 1)\cos (\phi (k) - \phi (k - 1))} \right] \end{split} (19) \Delta \gamma (k + 1) = \frac{{\gamma \Delta {h_{\text{m}}}(k + 1)}}{{\Delta {h_{\text{m}}}(k)}} (20) 式中：γ为狗腿角，（°）；Δγ为系统经过ts的狗腿角增量，（°）；
{h_{\text{m}}}(k) 为k时刻的测深，m。根据
\Delta {h_{\text{m}}}(k) 进行无迹卡尔曼滤波，KF3的状态方程和量测方程为：\begin{array}{l} \quad \alpha (k + 1) = \arccos [\cos (\gamma + \Delta \gamma (k + 1))\cos \alpha (k - 1) +\\ \dfrac{{\sin (\gamma + \Delta \gamma (k + 1))}}{{\sin \gamma }}(\cos \alpha (k - 1)\cos \gamma - \cos \alpha (k))] + {w_{\alpha (k)}} \end{array} (21) \begin{array}{l} \qquad\; \phi (k+1)=\phi (k)+\mathrm{sgn}(\phi (k)-\phi (k-1) \cdot \\ {\rm{arccos}}\dfrac{\mathrm{cos}(\Delta \gamma (k+1)-\mathrm{cos}\alpha (k)\mathrm{cos}\alpha (k{-1})}{\mathrm{sin}\alpha (k)\mathrm{sin}\alpha (k{-1})}+{w}_{\phi (k)} \end{array} (22) 式中：wα和wϕ分别为井斜角和方位角的系统高斯白噪声。
{\alpha _{{\text{KF3}}}} = \alpha {\text{(}}k + 1) + \nu {}_{\alpha (k)} (23) {\phi _{{\text{KF3}}}} = \phi {\text{(}}k + 1) + {\nu _{\phi (k)}} (24) 式中：αKF3和ϕKF3分别为KF3滤波后的井斜角和方位角，（°）；vα和vϕ分别为井斜角和方位角的系统观测噪声。
2.4 近钻头重力工具面角的估计
根据旋转测量原理，同一时刻的重力工具面角与磁工具面角的差与测量时刻的井斜角、方位角、地磁倾角呈现一定函数关系[12-13]。根据KF3求出的井眼井斜角和方位角计算磁性工具面角与重力工具面角的差Δω：
\Delta \omega = - 90 + \arctan \frac{{\sin {\phi _{{\text{KF}}3}}}}{{\cos {\alpha _{{\text{KF}}3}}\cos {\phi _{{\text{KF}}3}} - \tan \theta \sin {\alpha _{{\text{KF}}3}}}} (25) 根据Δω，计算旋近钻头动态重力工具面角估计值ωdg,e：
{\omega _{{\text{dg,e}}}} = {\omega _{{\text{m,KF3}}}} + \Delta \omega (26) 式中：ωdg,e为旋近钻头动态重力工具面角估计值，（°）；ωm,KF3为KF3滤波后的磁性工具面角，（°）。
2.5 磁干扰情况下的磁性工具面角
近钻头重力工具面角需根据x轴和z轴磁通门传感器的读数求出[14-15]，而磁通门测量结果不可避免地会受到周围电磁场的影响，为了降低井下钻具周围电磁场的影响程度，采用径向磁干扰的方法校正x轴和z轴磁通门的测量结果[16]。
磁场的干扰导致磁通门测量的磁场强度发生偏移和变形。磁干扰下的测量结果如图5所示。
在实际钻井过程中，井下仪器旋转一圈时，钻深可以忽略不计，可以看作仪器在原地旋转了一圈。z轴磁通门的测量结果可以认为没有发生变化，而x轴和y轴磁通门的测量值不断发生变化，如图2（a）所示。三轴磁通门传感器的测量数据记为（Bx，By，Bx），地球磁场可以看成一个固定值，即：
B_x^2 + B_y^2 + B_z^2 = {C^2} (27) 式中 ：C为常数。
根据椭圆校正原理，对短时间内采集的Bx，By进行磁干扰校正，得出排除磁干扰的Bxm和Bym：
{a_{x{\text{f}}}} = \max \left(1,\frac{{{B_{y\max }} - {B_{y\min }}}}{{{B_{x\max }} - {B_{x\min }}}}\right) (28) b{}_{x{\text{f}}} = \frac{{{B_{x\max }} - {B_{x\min }}}}{2} - {a_{x{\text{f}}}}{B_{x\max }} (29) B{}_{x{\text{m}}} = {B_x}{a_{x{\text{f}}}} + {b_{x{\text{f}}}} (30) {a_{y{\text{f}}}} = \max \left(1,\frac{{{B_{x\max }} - {B_{x\min }}}}{{{B_{y\max }} - {B_{y\min }}}}\right) (31) b{}_{y\text{f}}={a}_{y\text{f}} \left(\frac{{B}_{y\mathrm{max}}-{B}_{y\mathrm{min}}}{2}-{B}_{y\mathrm{max}}\right) (32) B{}_{y{\text{m}}} = {B_y}{a_{y{\text{f}}}} + {b_{y{\text{f}}}} (33) 式中：axf和ayf为x轴磁通门测量磁场强度的校正系数；bxf和byf为 y轴磁通门测量磁场强度的校正值，μT；Bxm和Bym为x轴和y轴排除磁干扰后的磁场强度，μT。
3. 试验与分析
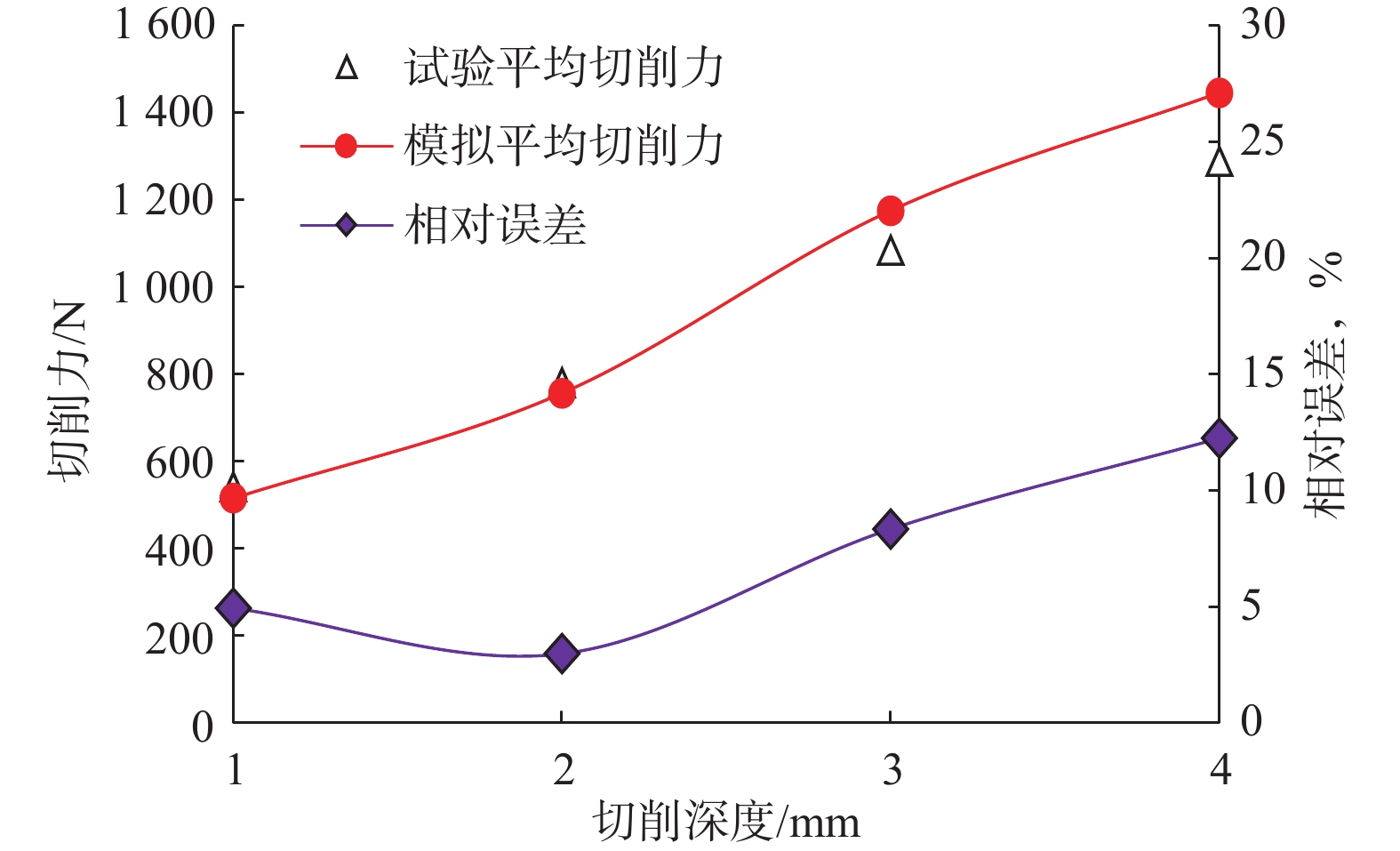
在实验室对NWD施加20～50 r/min转速、 1g～3g振幅的高斯白噪声振动信号，模拟井下钻进过程。采用上述测量方法测量井斜角和方位角，并与实际井斜角和方位角进行对比，结果见图6。由图6可以看出：测量井斜角与实际井斜角的最大误差为1.30°，最小误差为0.02°，平均误差为0.12°，方差为1.26°；测量方位角与实际方位角的最大误差为1.95°，最小误差为0.15°，平均误差为0.57°，方差为2.46°。
![]()
图 6 测量井斜角、方位角与实际井斜角、方位角的对比Figure 6. Comparison of measured and actual deviation angles and azimuths图7为采用上文测量方法（以下称为动态测量方法）测量工具面角、NWD探管直接测量工具面角与实际工具面角的差值。由图7可以看出，NWD探管直接测得工具面角与实际工具面角的差最大接近40°，已经不能满足测量近钻头伽马重力工具面角的要求，而采用动态测量方法测得的工具面角与实际工具面角的差小于10°，满足测量近钻头工具面角的要求。
![]()
图 7 动态测量和直接测量工具面角与实际工具面角的差值Figure 7. Difference between actual tool face angles and tool face angles measured by dynamic and direct methods在井斜角为0.5°、方位角度为142.818°，地磁场强度为53.74 μT、磁倾角为55.8°、磁性工具面角30°的测点，对NWD探管x、y方向分别施加0.1和0.2 μT的磁干扰，未进行磁干扰校正前测得磁性工具面角为23.56°，经过磁干扰校正后，磁性工具面角为29.82°，与真实工具面角相差0.18°。
为了验证动态测量方法的可行性和有效性，在某井3 800.00～4 100.00 m井段进行验证，首先在钻进过程利用动态测量方法测量井斜角、方位角和工具面角，然后再停钻测量井斜角、方位角和工具面角（下文称之为静态测量），然后对比静态和动态测量结果。因为钻具停止时没有旋转、振动和磁干扰，因此以静态测量结果为真实值。
图8为动态测得井斜角与静态测得井斜角的对比。由图8可以看出，动态测得井斜角与静态测得井斜角的平均误差为0.19°，方差为0.9342°。图9为动态测得方位角与静态测得方位角的对比。由图9可以看出，动态测得方位角与静态测得方位角的平均误差为1.19°，方差为1.943 642°。
![]()
图 8 动态测量井斜角与静态测量井斜角的对比Figure 8. Comparison of deviation angles measured by dynamic and static methods![]()
图 9 动态测量方位角与静态测量方位角的对比Figure 9. Comparison of azimuths measured by dynamic and static methods图10为动态测量工具面角与静态测量工具面角的对比。由图10可以看出，动态测得工具面角与静态测得工具面角的误差小于5°。
![]()
图 10 动态测量工具面角与静态测量工具面角的对比Figure 10. Comparison of tool face angles measured by dynamic and static methods以上分析可以得出，基于数据融合的井眼轨迹参数测量方法能够有效消除旋转、振动、磁干扰的影响，井斜角、方位角和工具面角的测量精度得到明显提高，满足了随钻地质导向对井眼轨迹参数测量的要求。
4. 结 论
1）针对旋转、振动、磁干扰对近钻头测量仪器的影响，提出了基于数据融合的井眼轨迹参数动态测量方法。该方法采用捷联式卡尔曼滤波器和磁干扰校正系统对测量信号进行滤波、校正，利用四元数法处理测量数据，求出近钻头井眼轨迹参数。
2）实验室模拟试验和现场试验均表明，基于数据融合的井眼轨迹参数动态测量方法可以消除旋转、振动、磁干扰的影响，使测得井眼轨迹参数的精度明显提高，满足了随钻地质导向对井眼轨迹参数测量的要求。
3）建议在现在研究成果基础上，进一步优化数据融合算法，比如基于机器学习的井眼轨迹预测模型，基于遗传算法的卡尔曼滤波器的参数调优。
-
![]()
图 2 试验切削力与模拟切削力对比
Figure 2. Comparison of cutting force results by experimental and simulated methods
![]()
图 3 锥形齿旋转冲击切削破岩过程
Figure 3. Rock-breaking process of conical cutting teeth under rotary impact
![]()
图 4 锥形齿扭转冲击破岩过程
Figure 4. Rock-breaking process of conical cutting teeth under torsional impact
![]()
图 6 冲击幅值对旋转冲击破岩方式下岩石破碎体积和破碎深度的影响
Figure 6. Influence of amplitude on rock-breaking volume and depth under rotary impact
![]()
图 7 扭转冲击幅值对扭转冲击破岩方式下岩石破碎体积和破碎深度的影响
Figure 7. Influence of amplitude on rock-breaking volume and depth under torsional impact
![]()
图 8 冲击频率对旋转冲击破岩方式下岩石破碎体积和破碎深度的影响
Figure 8. Influence of frequency on rock-breaking volume and depth under rotary impact
![]()
图 9 冲击频率对扭转冲击破岩方式下岩石破碎体积和破碎深度的影响
Figure 9. Influence of frequency on rock-breaking volume and depth under torsional impact
![]()
图 10 冲击幅值对不同破岩方式下破岩比功的影响
Figure 10. Influence of amplitude on rock breaking specific work by different rock-breaking methods
-
[1] 景英华,袁鑫伟,姜磊,等. 高速旋转冲击钻井破岩数值模拟及现场实验[J]. 中国石油大学学报(自然科学版),2019,43(1):75–80. JING Yinghua, YUAN Xinwei, JIANG Lei, et al. Numerical simulation and field experimental study on rock breaking in high speed rotating percussion drilling[J]. Journal of China University of Petroleum (Edition of Natural Science), 2019, 43(1): 75–80.
[2] CHENG Zhen, LI Gensheng, HUANG Zhongwei, et al. Analytical modelling of rock cutting force and failure surface in linear cutting test by single PDC cutter[J]. Journal of Petroleum Science and Engineering, 2019, 177: 306–316. doi: 10.1016/j.petrol.2018.09.023
[3] 玄令超,管志川,呼怀刚,等. 旋转冲击破岩实验装置的设计与应用[J]. 石油钻采工艺,2016,38(1):48–52. XUAN Lingchao, GUAN Zhichuan, HU Huaigang, et al. Design and application of experimental apparatus for rock breaking by rotary percussion[J]. Oil Drilling & Production Technology, 2016, 38(1): 48–52.
[4] CHE Demeng, ZHU Wule. Chipping and crushing mechanisms in orthogonal rock cutting[J]. International Journal of Mechanical Sciences, 2016, 119: 224–236. doi: 10.1016/j.ijmecsci.2016.10.020
[5] 王成勇,刘培德,胡荣生. 花岗岩切削破碎过程研究[J]. 岩石力学与工程学报,1991,10(2):185–196. WANG Chengyong, LIU Peide, HU Rongsheng. Study of granite cutting process[J]. Chinese Journal of Rock Mechanics and Engineering, 1991, 10(2): 185–196.
[6] 彭齐,周英操,周波,等. 凸脊型非平面齿PDC钻头的研制与现场试验[J]. 石油钻探技术,2020,48(2):49–55. PENG Qi, ZHOU Yingcao, ZHOU Bo, et al. Development and field test of a non-planar cutter PDC bit with convex ridges[J]. Petroleum Drilling Techniques, 2020, 48(2): 49–55.
[7] 孙源秀．锥形PDC齿破岩机理研究与新型钻头研制[D]．青岛: 中国石油大学（华东）, 2016． SUN Yuanxiu. Research on rock breaking mechanism of stinger cutters and new bits development[D]. Qingdao: China University of Petroleum(East China), 2016.
[8] 邹德永,郭玉龙,赵建,等. 锥形PDC单齿破岩试验研究[J]. 石油钻探技术,2015,43(1):122–125. ZOU Deyong, GUO Yulong, ZHAO Jian, et al. Experimental study on rock breaking of conical PDC cutter[J]. Petroleum Drilling Techniques, 2015, 43(1): 122–125.
[9] 邹德永,孙源秀,于鹏,等. 锥形齿PDC钻头台架试验研究[J]. 中国石油大学学报(自然科学版),2015,39(2):48–52. ZOU Deyong, SUN Yuanxiu, YU Peng, et al. Experiment study on bench test of stinger PDC bit[J]. Journal of China University of Petroleum (Edition of Natural Science), 2015, 39(2): 48–52.
[10] 汪为涛. 非均质地层锥形辅助切削齿PDC钻头设计与试验[J]. 石油钻探技术,2018,46(2):58–62. WANG Weitao. Design and test of a new PDC bit with tapered auxiliary cutter for heterogeneous formations[J]. Petroleum Drilling Techniques, 2018, 46(2): 58–62.
[11] 孙源秀,邹德永,徐城凯,等. 锥形聚晶金刚石复合片钻头(PDC)齿与常规PDC齿破岩效果对比试验[J]. 科学技术与工程,2015,15(36):159–162. doi: 10.3969/j.issn.1671-1815.2015.36.027 SUN Yuanxiu, ZOU Deyong, XU Chengkai, et al. Contrast experiment on conical PDC cutter and conventional PDC cutter[J]. Science Technology and Engineering, 2015, 15(36): 159–162. doi: 10.3969/j.issn.1671-1815.2015.36.027
[12] 谢晗,况雨春,秦超. 非平面PDC切削齿破岩有限元仿真及试验[J]. 石油钻探技术,2019,47(5):69–73. XIE Han, KUANG Yuchun, QIN Chao. The finite element simulation and test of rock breaking by non-planar PDC cutting cutter[J]. Petroleum Drilling Techniques, 2019, 47(5): 69–73.
[13] 邓勇．冲击载荷下深层致密砂岩破岩机理研究[D]．北京: 中国石油大学（北京）, 2017． DENG Yong. The research on rock fragmentation mechanism of deep tight sandstone under impact load[D]. Beijing: China University of Petroleum(Beijing), 2017.
[14] 祝效华,刘伟吉. 单齿高频扭转冲击切削的破岩及提速机理[J]. 石油学报,2017,38(5):578–586. doi: 10.7623/syxb201705011 ZHU Xiaohua, LIU Weiji. The rock breaking and ROP rising mechanism for single-tooth high-frequency torsional impact cutting[J]. Acta Petrolei Sinica, 2017, 38(5): 578–586. doi: 10.7623/syxb201705011
[15] 刘伟吉,曾义金,祝效华,等. 单齿复合冲击切削破岩机制及其与扭转冲击的对比[J]. 中国石油大学学报(自然科学版),2020,44(3):74–80. LIU Weiji, ZENG Yijin, ZHU Xiaohua, et al. Mechanism of rock breaking under composite and torsional impact cutting[J]. Journal of China University of Petroleum (Edition of Natural Science), 2020, 44(3): 74–80.
[16] 孙源秀,邹德永,侯绪田,等. 锥形PDC齿犁切破岩受力试验研究[J]. 石油机械,2014,42(9):23–26. doi: 10.3969/j.issn.1001-4578.2014.09.006 SUN Yuanxiu, ZOU Deyong, HOU Xutian, et al. Test of force of conical PDC cutter during rock plow-breaking[J]. China Petroleum Machinery, 2014, 42(9): 23–26. doi: 10.3969/j.issn.1001-4578.2014.09.006
[17] 祝效华,刘伟吉. 旋冲钻井技术的破岩及提速机理[J]. 石油学报,2018,39(2):216–222. doi: 10.7623/syxb201802010 ZHU Xiaohua, LIU Weiji. Rock breaking and ROP rising mechanism of rotary-percussive drilling technology[J]. Acta Petrolei Sinica, 2018, 39(2): 216–222. doi: 10.7623/syxb201802010
[18] DENG Yong, CHEN Mian, JIN Yan, et al. Theoretical and experimental study on the penetration rate for roller cone bits based on the rock dynamic strength and drilling parameters[J]. Journal of Natural Gas Science and Engineering, 2016, 36: 117–123. doi: 10.1016/j.jngse.2016.10.019
-
期刊类型引用(12)
1. 刘望，郭朝辉，蒋子璇，管锋，田海锋，李梓睿，夏雨生. 高速旋冲钻磨水泥塞提速机理及效率研究. 石油机械. 2025(04): 17-23 . 
百度学术
2. 田雨，张昕，张鹏翔，孙耀宁，许晨星，宋西岩. 冲击频率可调的钻井提速工具结构设计与试验. 石油机械. 2024(02): 36-43 . 百度学术
3. 张诗达，朱勇，高强，苏红. 旋冲钻井技术研究现状与展望. 排灌机械工程学报. 2024(05): 497-507 . 百度学术
4. 孙养清，易先中，万继方，易军，吴霁薇，刁斌斌，陈志湘. 机械式复合冲击器的工作特性分析. 石油机械. 2024(06): 29-37+108 . 百度学术
5. 陈炼，宋朝晖，王新东，张武涛，谢正森，粟籽华. 单牙轮钻头楔形牙齿偏转角优化方法. 石油钻探技术. 2023(01): 57-61 . 本站查看
6. 张文波，史怀忠，席传明，张楠，熊超，陈振良. 锥形PDC齿和常规PDC齿混合切削破岩试验研究. 石油机械. 2023(03): 33-39 . 百度学术
7. 闫炎，韩礼红，刘永红，杨尚谕，曹婧，牟易升. 全尺寸PDC钻头旋转冲击破岩过程数值模拟. 石油机械. 2023(06): 36-42 . 百度学术
8. 何超，邓虎，罗祝涛，李枝林，徐建超. 扭力冲击器流体仿真优化与试验. 钻采工艺. 2023(04): 26-32 . 百度学术
9. 王勇军，刘刚，佟铮，赵长亮，郑宇轩，冯守涛. 旋冲螺杆钻具在硬岩地热钻探中的应用研究. 钻探工程. 2023(05): 146-152 . 百度学术
10. 毛良杰，马茂原，刘立鹏，张伟，陈春宇. 扭力冲击器对钻柱黏滑振动的影响分析. 断块油气田. 2022(04): 545-551 . 百度学术
11. 王建云，韩涛，赵宽心，张立军，席宝滨，叶翔. 塔深5井超深层钻井关键技术. 石油钻探技术. 2022(05): 27-33 . 本站查看
12. 刘建华，令文学，王恒. 非平面三棱形PDC齿破岩机理研究与现场试验. 石油钻探技术. 2021(05): 46-50 . 本站查看
其他类型引用(6)
下载:
计量
- 文章访问数: 759
- HTML全文浏览量: 261
- PDF下载量: 125
- 被引次数: 18
