Casing Program Optimization and Drilling Matching Technologies for Horizontal Wells in Sulige Gas Field
-
摘要: 苏里格气田致密气藏埋藏深,钻遇地层塌漏问题突出,机械钻速低,前期水平井采用三开井身结构,难以达到钻井持续提速和降低钻井成本的目的。为此,在开展缩短中完周期、优化封固段和井眼尺寸等方面的理论分析,并进行井身结构优化过渡性方案现场试验的基础上,提出了井身结构优化思路,分析了可行性;然后,进行了封固段优选、井眼尺寸优化,设计了水平井小井眼二开井身结构。基于此井身结构,研究了井眼轨迹控制、个性化钻头和配套提速工具优选、强抑制高效润滑钻井液分段措施优化等关键钻井配套技术。该技术在19口井进行了现场应用,解决了长裸眼段“塌漏同存,上漏下塌”的问题,提高了各井段的机械钻速,大幅度缩短了钻井周期。研究结果表明,小井眼二开井身结构设计合理,钻井配套技术提速效果显著,可在苏里格气田水平井钻井中推广应用。Abstract: The tight gas reservoirs in Sulige Gas Field are characterized by deep buried depth, prominent collapse and leakage of drilling strata, low rates of penetration (ROP). Thus, with the three-section casing program of early horizontal wells, it is difficult to continuously increase the ROP and reduce the drilling cost. In response, a theoretical analysis was carried out on reducing the intermediate completion cycles and optimizing the sealing section and the borehole size. And a transitional test of casing program optimization was performed. On these basis, ideas for casing program optimization were proposed and their feasibility was analyzed. The sealing section and the borehole sizes were optimized, and a two-section casing program was designed for slim boreholes in horizontal wells. The key drilling matching technologies were studied, including borehole trajectory control, optimization of customized drill bits and matching speed-up tools, and segmentation measure optimization for drilling fluids with strong inhibition and high-efficiency lubrication. The field application proved that the proposed technologies had a good application effect and they solved the “collapse and leakage coexist, with leakage above and collapse below” problems in long openhole sections. The ROP in each section was improved, and the drilling cycle was greatly shortened. The application suggests that the two-section casing program for slim boreholes is reasonable, and the drilling matching technologies dramatically increase the ROP and therefore can be applied in horizontal well drilling in Sulige Gas Field.
-
Keywords:
- horizontal well /
- casing program /
- drilling /
- penetration rate /
- drilling fluid /
- lubricity /
- Sulige Gas Field
-
随着石油天然气的开发重点逐步向深层、超深层转变,井身结构也由三开、四开变为五开、六开甚至八开,部分开次井眼直径大;同时,钻遇窄压力窗口地层时易出现溢流,由于不清楚井筒内气液两相流动的规律,难以准确控制井筒压力。如塔里木油田某深井ϕ196.8 mm井段钻至吉迪克组出现溢流,因井眼容积大、气侵时间长,采用常规尺寸井眼两相流理论设计的压井参数压井,侵入气体排不净、涌漏交替,进行了多次压井。自20世纪中期,众多学者就气液两相流开展了大量研究工作,但大多集中于常规尺寸管道,与深井井眼尺寸相差较大。因此,有必要开展大尺寸环空中气液两相流动规律的研究,为深井溢流压井参数设计提供理论支撑。
迄今为止,对于气液两相流型方面的研究方法大体可以分为2大类,分别是试验法和数值模拟方法。M. Sadatomi等人[1]对外管内径30 mm、内管外径15 mm垂直环空中气液两相流的流型进行了研究和分析。V. C. Kelessidis等人[2]使用导电探针监测气液两相流动过程中的数据,并利用概率密度函数客观分析了试验中出现的流型。陈家琅等人[3]通过总结大量的室内试验数据和成果,依据流动过程中气相的流量,归纳出垂直环空中气液两相流的6种流型。林英松等人[4]使用外管内径120 mm、内管外径50 mm垂直环空来模拟井筒环境,进行了垂直环空中气液两相流的试验研究。张军等人[5]通过分析M. Caetano、V. C. Kelessidis等人的研究成果,发现了圆管与环空相似流型本质上的不同。
随着气液两相流理论的发展,利用计算流体力学(CFD)来研究圆形管道中多相流体的流动特性逐渐成为研究热点。R. I. Issa等人[6]利用数值模拟方法模拟了ϕ25.4 mm水平管中的气液两相流,模拟结果与1984年Taitel的理论预测结果较为接近,不过该模拟结果仅对小管径范围内的气液两相流有较高的适用性。之后,C. H. Newton等人[7]对ϕ50.0 mm水平管中的分层流动进行了数值模拟,模拟结果与Taitel−Dukler的预测结果较为吻合。赵铎等人[8]选用VOF模型开展了有关气液两相流型的模拟,其模拟结果与Mandhane的流型图较为吻合。彭壮等人[9]利用Fluent软件对垂直上升管道中气液两相的流动过程进行了数值模拟,发现在垂直管中主要出现搅拌流、细丝环状流和环状流,而泡状流和弹帽泡状流出现的次数极少。王海燕等人[10]为了提高气液两相流流型识别的准确性、建立了更高精度的气液两相流计算模型,以Kakol和Shoham的试验数据为研究基础,对最常用的3种流型判别方法进行了对比和归纳。张馨玉[11]对垂直上升管内不同流动介质、不同管径以及不同倾角情况下的气液两相流进行了数值模拟。邱小雪等人[12]模拟了产量较低积液气井气液两相的流动情况,分析了不同积液量、气相表观速度工况下井筒内持气率的变化规律,建立了相应的数学模型,用来预测气井的产气规律,并可据此调整生产方案。俞强强等人[13]利用Fluent软件模拟了ϕ20 mm竖直圆管中的气液两相流,发现在一定气、液相表观流速下,出现了气泡流、段塞流、搅拌流和环状流。
综合国内外研究成果来看,对于环空管内气液两相流的相关研究主要从20世纪80年代才逐步展开,数值模拟方面的研究则起步更晚。此外,多数研究都是在几十毫米管径的基础上开展的,从目前已公开发表的文献来看,针对大尺寸环空内气液两相流动的研究相对匮乏[14],A. R. A. Colmanetti等人[15]研究了油包水和水包油在垂直管中的流型转化现象,结果表明,管道的几何形状明显影响流型的转化。A. R. A. Colmanetti等人[16]气液两相流流动试验采用的垂直环空管道外径为155 mm,内径为60 mm,是现有文献中最大尺寸的环空管道。随着深井、超深井的增多,钻遇气侵等复杂工况概率大,如果现场缺乏大尺寸环空气液两相流动理论支撑,井筒压力控制难度增大,处理成本将会增加。因此,笔者利用Fluent软件中的VOF模型对大尺寸环空内气液两相的流动规律进行了数值模拟,分析了每种流型的特征,建立了大尺寸环空内气液两相流型的转化判据,揭示了环空内气液两相的流动规律,开展了基于不同尺寸环空流型转化理论的压井模拟,为深井、超深井钻井溢流压井提供了理论支撑。
1. 数值模拟方法
1.1 控制方程
当研究着重于各相之间界面现状或者界面附近的流型时,Fluent中的VOF模型则可以作为多相流模型中一个非常好的选择。常见的如液相中气泡的运动、分层流动或自由液面流动等,多选用VOF模型作为流动模型。
该模型的基础是各流动介质之间不存在相互穿插、互不相容,即各流相体积比之和在任一控制体积内始终保持1,即:
αl+αg=1 (1) 在气液两相流动的情况下,可在式(1)的基础之上,用流体体积函数方程来表示其间的数学关系:
\frac{\partial\alpha_x}{\partial t}+\nabla\cdot\left(\alpha_x\boldsymbol{u}_x\right)=\frac{M_x}{\rho_x} (2) 式中:αl为液相体积分数;αg为气相体积分数;αx为控制体容积之中x相(气或液)所占的体积分数;ux为控制体容积之中x相(气或液)的速度,m/s;t为时间,s;Mx为两相之间传递的质量,kg/(m³·s);ρx为x相(气或液)的密度,kg/m³。
质量守恒方程:
\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho {\boldsymbol{u}}) = 0 (3) 式中:ρ为密度,kg/m³;u为速度,m/s。
动量守恒方程:
\frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{{\partial {{\boldsymbol{\tau }}_{ij}}}}{{\partial {x_j}}} + \rho {g_i} + {F_i} (4) 式中:ui,uj分别为i和j方向的速度,m/s;p为静压,MPa;τij为应力张量,MPa;ρgi为i方向上的重力体积力,N;Fi为i方向上的外界体积力,N。
1.2 几何模型
本文研究的是垂直向的环空管道,建立的物理模型如图1所示。进行多次模拟后,发现气液两相在管路中流动2.0 m左右即可达到稳定流。因此考虑Fluent的运算速度,建立长度6 m的环空管道模型,环空外径301.6 mm,环空内径104.8 mm,环空水力当量直径196.8 mm,气相和液相从底部流入环空,环境压力为101 325 Pa,环境温度为293.15 K。
1.3 网格划分
大尺寸环空模型进行网格划分时,考虑流体边界层对流体流动的影响,在牛顿内摩擦系数的作用下,靠近壁面的流动为层流,内部为湍流,因此插入边界层膨胀网格,以更好地模拟流体在壁面的流动情况。网格剖分选择插入面网格选项,并通过膨胀选项预设模型内外壁面处边界层参数,生成如图2所示的网格模型。整体环空模型网格单元数量为3.6×106,平均正交质量为0.999 78。
1.4 模型选择与边界条件
选用压力基瞬态求解器,基于VOF方法对气液两相流动进行数值模拟。湍流模型选择 SSTκ-ω模型,同时为保证求解精度,动量方程和湍动能方程使用二阶迎风格式,压力采用PRESTO进行离散,压力−速度耦合方法选用SIMPLEC算法,并将Z轴重力加速度设为-9.81 m/s2,确定各边界条件为:环空入口界面设定为质量流量入口,出口界面设定为压力出口,内外壁面分别设定为固体壁面,其中水力直径设定为196.8 mm,数值模拟流体的物性参数如表1所示。
表 1 数值模型流体的物性参数Table 1. Physical properties parameters of fluid for numerical simulation流体 密度/(kg·m−3) 黏度/(mPa·s) 表面张力/(N·m−1) 水 998.2 1.003 0.072 空气 1.225 1.798×10−2 1.5 网格无关性验证
数值模拟中将水力当量直径196.8 mm环空数值模型划分为310×104,340×104,370×104,400×104和430×104等5种数量的网格,进行数值模拟,为了保证气液两相流动得到充分发展,监测离入口4 m的横截面有气相通过后8 s内的平均含气率。保持液相表观速度为0.05 m/s,改变气相表观速度,数值模拟结果如图3所示。从图3可以看出,当网格数量达到370×104后,该截面在3种工况下的平均含气率基本不变,因此可以认为此时与网格不具有相关性。故在后续的模拟计算中网格数量选择370×104。
1.6 模拟方法验证
为了验证数值模拟方法的可靠性,利用文献[16–17]中的室内试验数据进行验证,采用与上述水力当量直径196.8 mm模型相同的求解器及参数设置方法,建立了与文献中试验装置尺寸相同的水力当量直径57.0和95.0 mm的环空模型。
1)文献[17]中试验环空的模型,环空外径120 mm,内径63 mm,环空水力当量直径57 mm。当气相表观流速为
0.0606 m/s、液相表观速度为0.0491 m/s时,环空内气体等值面及不同截面的含气率如图4所示,试验及模拟含气率的对比如图5所示。在该流速条件下,文献[17]中试验观察到的流型是泡状流。从图4可以看出,相同流速下模拟得到的流型也是泡状流。从图5可以看出,模拟含气率的变化趋势与试验测得含气率一致,吻合较好。
2)文献[16]试验环空的模型,环空外径155 mm,内径60 mm,水力当量直径95 mm。模拟结果和试验结果如表2所示。从表2可以看出,各工况下模拟得到的流型与试验结果一致,验证了模拟方法的正确性和可行性。
表 2 不同工况下的数值模拟结果与试验结果Table 2. Comparison between numerical simulation results and experimental data under different workingconditions工况 气相表观
速度/(m·s−1)液相表观
速度/(m·s−1)数值模拟流型 试验流型 a 0.125 0.025 泡状流 泡状流 b 0.150 0.030 泡状流 泡状流 c 0.150 0.100 弹帽流 弹帽流 d 1.000 0.030 搅拌流 搅拌流 2. 大尺寸环空气液两相流数值模拟流型特征分析
基于水力当量直径196.8 mm大尺寸环空模型,通过调整入口边界气相和液相的质量流量,模拟得到了泡状流、弹帽流、段塞流和搅拌流等4种流型。利用Fluent软件的后处理模块,分析同一流型中某一工况下模拟结果的特征。
2.1 泡状流特征分析
模拟液相表观速度0.50 m/s、气相表观速度0.10 m/s工况下环空中气液的流动情况,发现此工况下环空中的流型为泡状流。环空中含气率等值面和环空径向界面气液两相分布如图6、图7所示。
从图7可以看出,在不间断、保持连续的液相之内,气相以远小于环空区域尺寸的小型气泡存在;气泡的尺寸并不统一,较大尺寸的气泡呈椭球形,部分呈现短粗的锥形外观;较小尺寸的气泡既有细长形,也有扁长形。随着流相介质不断向上流动,小尺寸气泡有聚合成较大尺寸气泡的趋势。
从图7还可以看出:在充满水(蓝色相)的环空区域内,气泡分布较为均匀;含气率高的较大尺寸气泡周围充斥着更大面积的连续水相,且气泡截面更接近圆形;而尺寸较小的、截面形状不规则的气泡则以更密集的方式分布,远离较大气泡但彼此间隔极小甚至连续。泡状流型下气相分布弥散,且形成的气泡比较小。
该工况下气液两相流流经环空内截面(距离入口3 m处)时的含气率均值约为0.103,含气率随时间波动的曲线如图8所示。从图8可以看出,含气率整体变化较为平稳,波峰与波峰相隔较近,符合环空内泡状流气相分布特征。
2.2 弹帽流特征分析
模拟液相表观速度0.05 m/s、气相表观速度0.15 m/s工况下环空中气液的流动情况,发现环空中的流型为弹帽流,如图9所示。
从图9可以看出,当液相流量较小、气相流量较大时,环空中的气泡尺寸明显变大,且大尺寸气泡与小尺寸气泡体积相差较大。其中,较大尺寸气泡不再呈现椭球形(见图10),而是气泡上部发展成锥帽形,气泡底部则相对扁平或者轻微内凹,呈明显的弹帽流结构形式,一部分弹帽状气泡与另一部分弹帽状气泡之间夹杂着一小段体积极小的气泡,即环空内气相分布不均匀,液相连续性变差。
从图10可以看出,弹帽状大气泡都不同程度地靠近环空内壁,气泡与壁面之间仅存在一层薄薄的液膜。综合该现象与图中气泡分布区域,进一步表明环空内气液分布的不均匀性。
同时对比常规尺寸环空的气液两相流型,常规尺寸环空中并未发现有弹帽流。当气相流量增大时,气泡聚集并拢,但由于环空区域较大,大气泡与大气泡之间很难进一步聚并,远达不到形成段塞流中泰勒泡的尺寸。
该流动结构下,环空截面含气率均值为0.242,变化曲线如图11所示。从图11可以看出,含气率波动起伏较大,与弹帽状气泡分布相对应——高波峰段曲线之间存在一小段峰谷差值更小的起伏段,符合环空内弹帽流气相分布特征。
2.3 段塞流特征分析
模拟液相表观速度0.50 m/s、气相表观速度0.50 m/s工况下环空中气液的流动情况,发现环空中的流型为段塞流,如图12所示。环空内气液两相流动表现出直观的段塞流结构,环空区域的上、中、下部分各存在一个明显的大泡——泰勒泡,结合图13可以看出,大气泡轴向长度大于环空外管直径,呈典型的段塞流泰勒泡结构。
在该流型下,存在泰勒泡的区域内气相占据大部分流道体积,形成类似气塞的结构;而泰勒泡与泰勒泡之间存在微小游离气泡,可以看作液相形成的液塞,液塞段与气塞段交替向上流动。
从图13可以看出:环空内的气液两相流动不具有对称性的特点;靠近环空外壁的泰勒泡一侧存在一定厚度的液膜;而另一侧紧挨着环空内壁,液膜极薄,环空内的气液两相分布无论在轴向还是径向都表现出极高的不均匀性,液相的连续性变得更差。
该流动条件下,环空截面含气率平均达到0.436,变化曲线如图14所示。曲线整体都在较高水平范围内波动;曲线波动趋势与弹帽流工况下类似,但由于液塞与气塞的存在,曲线波动幅更大,符合环空内段塞流气相分布特征。
2.4 搅拌流特征分析
模拟液相表观速度0.1 m/s、气相表观速度2.0 m/s工况下环空内气液的流动情况,发现环空内的流型为搅拌流,气液两相分布具有混乱、无序的特点,如图15所示。
随着大量气体以较大流速流入环空区域,气相在环空内聚集成泰勒泡的同时又产生二次聚合——泰勒泡之间彼此连接、整体变得窄长,周围的小气泡也互相聚集成细长外形,混合在泰勒泡周围。
由于泰勒泡更加窄长、外形扭曲,在高流速下气泡稳定性降低,被不断搅碎又反复聚合。气相与液相互相掺杂,整体流动呈现无序、混乱且带有一定间歇性的特点,气液两相交界面形状极不规则,环空流道内两相分布无明显区域性和规律性,如图16和图17所示。从图17可以看出,气相多聚集分布在靠近内壁附近,通过对比气液两相分布云图(见图16),能直观地看出环空内搅拌流流型下气液两相流动和分布的混乱无序性,即气相有一个明显的搅碎混合到聚集混合的分布变化。
该流动条件下,搅拌流流经特定截面的平均含气率为0.564,远高于前3种流型,变化曲线如图18所示。从图18可以看出,随着气液两相流流动发展,特定截面的含气率在保持一段时间较高值(此时气相聚集,截面含气率高)后,会经历短时间含气率下降幅值较大的阶段(此时气相被搅碎,通过截面的气泡量减少,含气率降低),并且2个阶段在时间间隔上无明显等距,表现出无序性的脉动发展,符合环空内搅拌流气相分布特征。
结合不同流型的气相等值面图、截面含气率云图及截面含气率波动曲线特征,对每种工况进行流型划分,绘制了水力当量直径196.8 mm环空中气液两相流型的分布图(见图19)。
3. 大尺寸环空气液两相流型转化判据
3.1 泡状流转化为弹帽流的判据
P. Griffith等人[18]所做的试验表明,泡状流向段塞流的转变发生在含气率为0.25~0.30时。N. A. Radovcich等人[19]研究认为,当离散气泡的碰撞频率很高时,泡状流将会向段塞流转变,并提出半理论的判别方法,认为这一转变发生在含气率为0.30时。V. C. Kelessidis等人[2]预测含气率为0.25时,泡状流转化为段塞流。结合本文的数值模拟结果综合分析,认为泡状流向弹帽流转化的临界含气率为0.25。
设气泡的上升速度为vg,则它与气相表观速度vsg之间的关系为:
{v_{{\text{sg}}}} = \alpha {v_{\text{g}}} (5) 类似地,液相平均速度vl与液相表观速度vsl之间的关系为:
{v_{{\text{sl}}}} = (1 - \alpha ){v_{\text{l}}} (6) 设v0是气泡相对于液相的上升速度,则:
{v_{\text{g}}} = {v_{\text{l}}} + {v_0} (7) 液相速度低时,气泡足够大,其上升速度与气泡的尺寸无关,而只与两相的物理性质有关。T. Z. Harmathy[20]指出,在无限大介质中,单个气泡的上升速度
{v_{0\infty }} 为:{v_{0\infty }} = 1.53{\left[ {\frac{{g({\rho _{\text{l}}} - {\rho _{\text{g}}})\sigma }}{{\rho _{\text{l}}^{\text{2}}}}} \right]^{\tfrac{1}{4}}} (8) 式中:vg为气泡的上升速度,m/s;vsg为气相表观速度,m/s;α为含气率;vl为液相平均速度,m/s;vsl为液相表观速度,m/s;v0为气泡相对于液相的上升速度,m/s;ρl为液相密度,kg/m³;
{v_{0\infty }} 为单个气泡的上升速度,m/s;ρg为气相密度,kg/m³;σ为表面张力,N/m;g为重力加速度,m/s2。N. Zuber等人[21]指出,气泡群中单个气泡的上升速度
{v_0} 应为:{v_0} = {(1 - \alpha )^{\tfrac{1}{2}}}{v_{0\infty }} (9) 联立以上公式,得:
{v_{{\text{sl}}}} = \frac{{1 - \alpha }}{\alpha }{v_{{\text{sg}}}} - {(1 - \alpha )^{1.5}}1.53{\left[ {\frac{{g\left( {{\rho _{\text{l}}} - {\rho _{\text{g}}}} \right)\sigma }}{{\rho _{\text{l}}^{\text{2}}}}} \right]^{0.25}} (10) 令
\alpha =0.25,代入数据,即可得到泡状流转化为弹帽流的判据:{v_{{\text{sl}}}} = 3{v_{{\text{sg}}}} - 0.994{\left[ {\frac{{g\left( {{\rho _{\text{l}}} - {\rho _{\text{g}}}} \right)\sigma }}{{\rho _{\text{l}}^{\text{2}}}}} \right]^{0.25}} (11) 3.2 弹帽流转化段塞流的判据
参考已有的泡状流—段塞流转化判据,基于段塞流漂移速度模型,同时结合本文的数值模拟结果综合分析,认为这一转变发生在含气率为0.45时,并建立弹帽流转化为段塞流的新判据:
{v_{{\text{sl}}}} = \left( {\frac{1}{{\alpha {C_{\text{0}}}}} - 1} \right){v_{{\text{sg}}}} - \frac{{0.247\sqrt {g{D_{\text{h}}} \dfrac{\Delta\rho}{\rho _{\text{l}}}} }}{{{C_{\text{0}}}}} (12) 式中:Dh为当量直径,m;Δρ为气液两相密度差;kg/m³;C0为分布系数。
其中,式(12)推导过程运用了漂移速度模型:
v_{\text{gm}}=C_0\left(v_{\text{sl}}+v_{\text{sg}}\right)+0.35\sqrt{gD_{\text{h}}\dfrac{\Delta\rho}{2\rho}\mathrm{_l}} (13) {C_0} = \left( {1.2 - 0.2\sqrt {\frac{\rho _{\text{g}}}{\rho _{\text{l}}}} } \right) (14) 代入数据,即可得到弹帽流转化为段塞流的判据:
{v_{{\text{sl}}}} = \left( {\frac{{20}}{{10.8 - 1.8\sqrt {\dfrac{\rho _{\text{g}}}{\rho _{\text{l}}}} }} - 1} \right){v_{{\text{sg}}}} - \frac{{0.247\sqrt {g{D_{\text{h}}} \dfrac{\Delta\rho} {\rho _{\text{l}}}} }}{{1.2 - 0.2\sqrt {\dfrac{\rho _{\text{g}}}{\rho _{\text{l}}}} }} (15) 3.3 段塞流转化为搅拌流的判据
V. C. Kelessidis等人[2]通过试验观察发现,环空中的搅拌流与Y. Taitel等人[22]所描述圆管入口段的流动类似。两相混合物注入的地方可以观察到搅拌流,其后又可以见到稳定的段塞流。
Y. Taitel等人[22]指出:当液体段塞的长度小于临界稳定段塞长度时,将会出现搅动流;稳定段塞的长度是圆管直径的16倍。圆管中的试验表明,液体段塞长度与管径之比基本上为一常数,但不同研究者所报道的该值却不相同,M. Ozawa等人[23]报道的为7.5,Y. Taitel等人[22]报道的为16。
将垂直圆管中泰勒气泡的追赶模型用于环空,得到:
\frac{{{L_{\text{e}}}}}{{{D_{\text{h}}}}} = 22.96\left( {C\frac{{{v_{\text{m}}}}}{{{v_{{\text{rc}}}}}} + 1} \right) (16) 式中:Le为液塞长度,m;vm为气液混合物的速度,m/s;vrc为气泡在环空静止液体中的上升速度,m/s;C为常数。V. C. Kelessidis等人[2]的试验表明,vrc为0.37 m/s,C为1.55。
在流型转变中,结合本文的数值模拟结果综合分析,认为这一转变发生在含气率为0.6时,Le/Dh取108,建立弹帽流转化为段塞流的新判据:
{v_{{\text{sl}}}} = \left( {\frac{{{L_{\text{e}}}}}{{35.59{D_{\text{h}}}}} - 1} \right) - {v_{{\text{sg}}}} (17) 3.4 大尺寸环空气液两相流流型转化判据验证
将3.3节建立的泡状流转化为弹帽流、弹帽流转化为段塞流和段塞流转化为搅拌流的判据绘制在流型图中,结果如图20所示。从图20可以看出,上文建立的垂直环空气液两相流流型转化判据与模拟结果吻合得较好。
4. 大尺寸环空气液两相流型影响因素分析
4.1 气相表观速度对流型转化的影响
前文已分析不同工况下4种流型的特征,本节将选取液相表观速度为0.05 m/s、不同气相表观速度的工况,讨论气相表观速度对各流型之间转化的影响,工况及模拟结果见表3。
表 3 液相表观流速为0.05 m/s时,不同气相表观流速下流型模拟结果Table 3. Flow pattern simulation results under different apparent gas-phase flow velocities when apparent liquid-phase flow velocity is 0.05 m/s液相表观速度/(m·s−1) 气相表观速度/(m·s−1) 数值模拟流型 0.05 0.08 泡状流 0.15 弹帽流 0.85 段塞流 2.10 搅拌流 图21所示为入口边界液相表观速度保持不变,气相表观速度分别为0.08和0.15 m/s时环空中含气率等值面。从图21可以看出:气相表观速度较小气体主要以小的离散状态气泡分布在环空流道中,流动平稳,小气泡并未挤碰并拢;当气相表观速度增大时,气液两相混合介质在环空内的流动状况开始加剧,气液两相交界面逐渐受到扰动,环空流道内出现更不规则的气泡,由于扰动增强并逐渐积累,部分气泡接触融合成尺寸更大、特点不同的气弹,即随着气相表观速度增大,易受扰动的分散气泡聚并成为帽型气泡,逐步发展成弹帽流。
入口液相表观速度保持不变,气相表观速度分别为0.15和0.85 m/s时,环空中的含气率等值面如图22所示。从图22可以看出:气相表观速度进一步增大,具有一定规模的弹帽状气泡因两相混合流体中气相带来的更大扰动而发生碰撞聚并;当弹帽状气泡聚并达到泰勒泡的尺寸界限时,弹帽流就发展转变为段塞流。
入口液相表观速度保持不变,气相表观速度分别为0.85和2.10 m/s时,环空中含气率等值面如图23所示。从图23可以看出:气相表观速度继续增加,显著提高了环空内的含气率,此时气相交界面聚并更加频繁。同时,紊流下的扰动提高,窄长的泰勒泡被打碎破坏,气相交界面稳定性变差,段塞流特征基本消失,环空内发展出现了搅拌流。
4.2 液相表观速度对流型发展的影响
气相表观速度保持0.15 m/s不变时,模拟液相表观速度为0.02,0.10和0.50 m/s时的流型和含气率等值面,结果如表4和图24所示。
表 4 气相表观流速为0.15 m/s时,不同液相表观流速下流型模拟结果Table 4. Flow pattern simulation results under different apparent liquid-phase flow velocities when apparent gas-phase flow velocity is 0.15 m/s气相表观速度/(m·s−1) 液相表观速度/(m·s−1) 数值模拟流型 0.15 0.50 泡状流 0.10 弹帽流 0.02 段塞流 由表4可知,保持气相表观速度不变的情况下,随着液相表观速度减小,环空内分别呈现出泡状流、弹帽流和段塞流3种流型。
从图24可以看出:当液相表观速度为0.50 m/s,流速相对较大时,气相在流道内被冲散,气液两相交界面密集,气相以分散小气泡的形式较均匀地在液相中向上流动;当液相表观速度减小时,由于黏性和惯性力等作用,气相在液相中表现出更强的滞留性,分散的小气泡会随着流动慢慢聚并形成大尺寸气泡,并发展转变成弹帽流或段塞流。
4.3 环空尺寸对流型转化的影响
将图20与V. C. Kelessidis等人[2]、G. Das等人[24]建立的常规尺寸环空气液两相流型转化边界相比,大尺寸环空内泡状流的气相表观速度范围增大,段塞流向搅拌流转化所要求的气相表观速度也有所增大,且泡状流与段塞流之间存在过渡流型——弹帽流,各流型转化边界均有不同程度的右移。
模拟气相表观流速为1.00 m/s、液相表观速度为0.03 m/s时,水力当量直径95.0,196.8和282.6 mm环空中的气液分布情况,结果如图25所示。
从图25可以看出:在水力当量直径95.0 mm的环空中已形成了大的泰勒泡,属于段塞流;水力当量直径196.8和282.6 mm的环空中还未形成泰勒泡,还是以弹帽泡为主的弹帽流。这和图20与常规尺寸环空流型转化边界对比得到的结论类似。较小尺寸环空更容易发生气泡的聚并并形成泰勒泡,主要原因是当气液相表观速度不变的情况下,气泡尺寸受到环空尺寸的影响,达不到流型转化的含气率要求;随着环空尺寸增大,重力作用也更加明显,混合流体惯性力作用效果减弱,整体扰动和紊乱程度降低;表面张力的作用逐渐减弱,气液两相交界面更加稳定。总体来说,随着环空尺寸增大,气液两相分布较均匀,稳定流型的占比增加,相对减弱了气相流量的影响。
5. 压井模拟
塔里木盆地某深井ϕ301.6 mm井段使用ϕ104.8 mm钻杆钻进,环空水力当量直径为196.8 mm,钻至井深
4800 m时,钻遇异常高压地层,发生溢流,钻井液池中的钻井液体积增加0.5 m3,随后关井,进行压井,压井过程中涌漏交替,多次调整压井参数压井,最后压井成功。笔者以该井实际井身结构、压井参数为例进行模拟,以孙宝江等人[25–26]建立的多相流动模型为主方程,以原辅助方程、第3节建立的新流型转化判据为辅助方程进行模拟,并对比模拟结果。原始钻井液密度为1.70 kg/L,排量为50 L/s,黏度为40 mPa·s。图26所示为该井不同密度压井液压井时环空内含气率的分布。基于大尺寸环空判据设计的压井液密度为1.75 kg/L,基于常规尺寸环空判据设计的压井液密度为1.77 kg/L。从图26可以看出:采用密度1.70 kg/L钻井液循环时,井筒内始终存在气体;采用密度1.75 kg/L的压井液将2 000~4 800 m井段的侵入气体循环出井口,井底已不再进气,继续循环,可以将井内侵入气体全部排出;密度1.77 kg/L的压井液将900~3 500 m井段的侵入气体排出井口后,井底又开始有气体侵入,分析其原因可能是刚开始循环压井时,密度1.77 kg/L压井液的液柱压力加上环空摩阻大于地层压力,气体不再进入井筒,开始循环排出已侵入气体时,井底压力超过了漏失压力,井筒内产生漏失,导致井底压力降低;同时,随着气体向上运移、体积膨胀,导致井底压力进一步降低,最终井底压力又低于地层压力,又有气体侵入井筒,发生溢流,即发生了涌漏交替的复杂情况。相同气侵条件下,常规尺寸环空的流型转化理论认为井筒内气液分布更复杂一些,若出现气液交替的段塞流情况,需要压井液密度大一些。而大尺寸环空的流型转化理论预测井筒内是弹帽泡、气泡小,相对容易处理,需要的压井液密度就小一些。从模拟情况来看,基于新流型转化判据设计的压井液密度更适用于窄安全密度窗口、大尺寸环空溢流压井的情况。
6. 结 论
1)基于VOF模型,建立了大尺寸环空气液两相流动数值模拟方法,利用文献中的数据,验证了该方法的可靠性与正确性。
2)利用建立的数值模拟方法模拟大尺寸环空中的气液流动,发现环空可出现了泡状流、弹帽流、段塞流和搅拌流。从含气率等值面、截面含气率云图等角度揭示了每种流型的变化特征,据此绘制了水力当量直径196.8 mm环空内气液两相流型图,并结合大尺寸环空气液两相流型转化临界含气率和流型变化特征,创建了流型转化判据。
3)与常规环空尺寸的流型转化边界对比发现,对于大尺寸环空,流型图中泡状流、弹帽流的占比大,流型转化边界沿气相流量增大方向不同程度右移。
4)由于常规尺寸环空两相流理论考虑的气液分布情况更复杂一些,基于该理论设计的大尺寸环空的压井液密度偏大,会导致涌漏交替。采用文中建立的新判据设计的压井液密度适用于窄安全密度窗口、大尺寸环空压井。
-
表 1 不同尺寸钻头钻进1 000 m时的破岩能耗
Table 1 Rock breaking energy consumption for drilling 1 000 m with bits in different sizes
钻头外径/mm 理论破岩面积/mm2 机械比能/MPa 钻压/kN 转速/ (r·min–1) 扭矩/(kN·m) 机械钻速/(m·h–1) 破岩总体积/m3 消耗总能量/J 152.4 18 232.22 0.038 9 100 70 4.06 15 18.23 7 093.43 152.4 18 232.22 0.032 5 100 70 4.06 18 18.23 5 932.04 215.9 36 591.06 0.027 4 100 70 5.76 15 36.59 10 040.59 215.9 36 591.06 0.022 8 100 70 5.76 18 36.59 8 355.20 222.2 38 757.68 0.026 6 100 70 5.92 15 38.76 10 293.26 222.2 38 757.68 0.022 1 100 70 5.92 18 38.76 8 584.05 228.6 41 022.50 0.025 8 100 70 6.08 15 41.02 10 573.14 表 2 不同井身结构下的排量计算结果
Table 2 Flow rates calculated with different casing programs
井身结构 井筒容积/
m3井筒容积
增量/m3单井岩屑量/
m3岩屑增量/
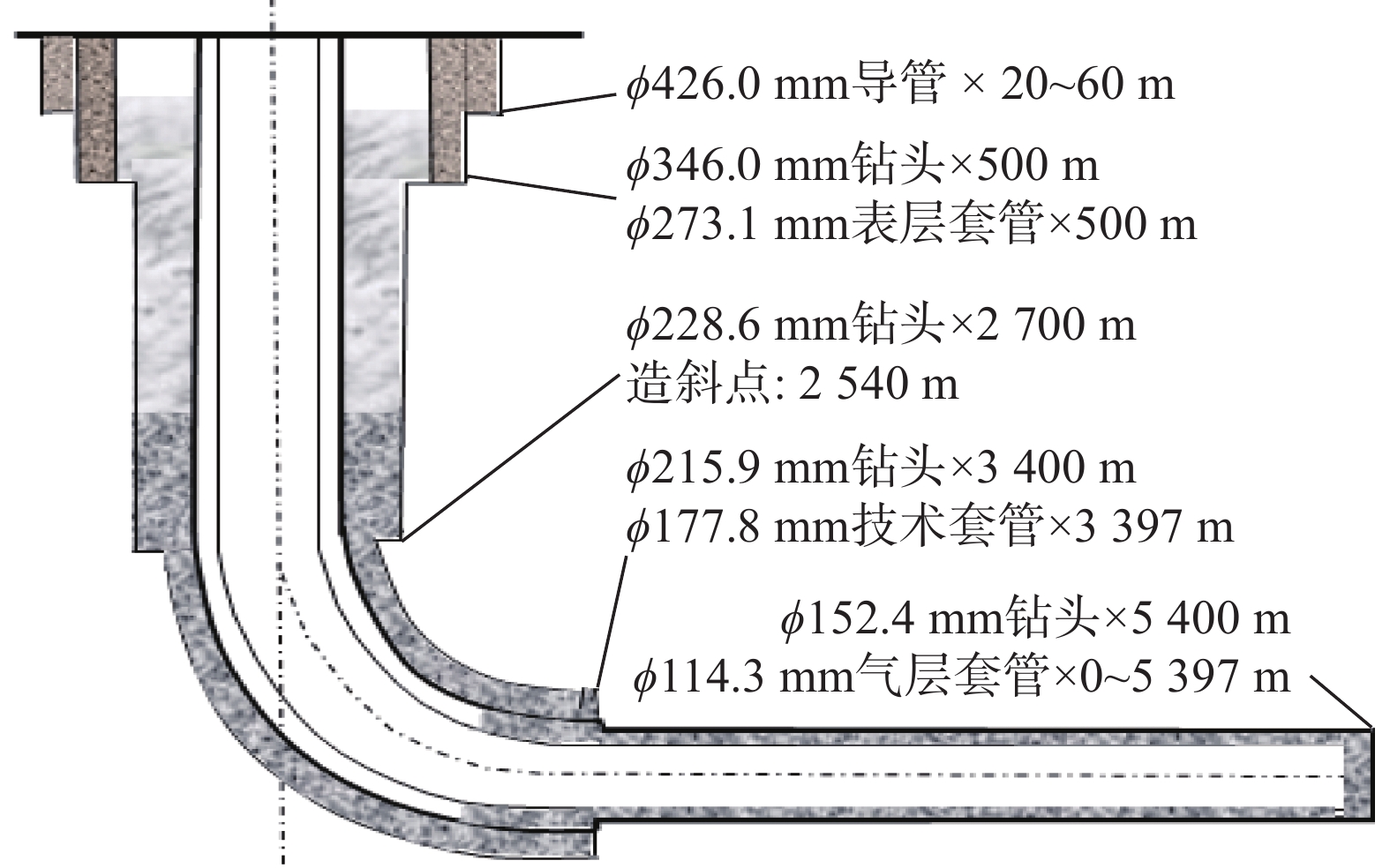
m3三开 190.2 47.7 655.25 25.25 常规井眼二开(过渡) 248.0 105.5 946.50 316.50 小井眼二开(先导) 142.5 630.00 注:三开结构为ϕ346.0 mm×500 m/ϕ273.1 mm×500 m+(ϕ228.0 mm×2 200 m +ϕ215.9 mm×700 m)/ϕ177.8 mm×3 400 m+ϕ152.4 mm×1 500 m/ϕ114.3 mm×4 900 m;常规井眼二开(过渡)结构为ϕ346.0 mm×1 200 m/ϕ273.1 mm×1 200 m+ϕ215.9 mm×3 700 m/ϕ139.7 mm×4 900 m;小井眼二开(先导)结构为ϕ215.9 mm×2 600 m/ϕ177.8 mm×2 600 m+ϕ152.4 mm×2 300 m/ϕ114.3 mm×4 900 m。 表 3 靖50-21H2井的井身结构设计结果
Table 3 Casing program design for Well Jing50-21H2
开钻次序 钻头外径/mm 井深/m 套管外径/mm 套管下入层位 套管下深/m 水泥浆返高 导管 346.0 50 273.1 第四系 50 地面 一开 215.9 2 584 177.8 石千峰组 2 584 地面 二开 152.4 5 251 114.3 石盒子组 0~5 248 气层以上500 m 表 4 大功率螺杆与常规螺杆的参数对比
Table 4 Parameter comparison between high-power screwdrill and conventional screwdrill
钻具型号 外径/
mm排量/
(L·s–1)转速/
(r·min–1)工作压降/
MPa最大压降/
MPa输出扭矩/
(N·m)最大输出扭矩/
(N·m)输出功率/
kW7LZ172×1.5°(普通螺杆) 172.0 19.5~39.5 84~168 4.0 5.65 7 176 10 137 150 7LZ172×1.5°(等壁厚螺杆) 19.5~39.5 88~177 5.5 7.85 9 866 14 288 238 5LZ127×1.5°(普通螺杆) 127.0 10.7~21.5 140~280 4.0 5.65 2 344 3 312 87 7LZ127×1.5°(普通螺杆) 12.35~24.70 130~261 3.2 4.52 2 468 3 277 75 表 5 小井眼二开与典型三开井身结构完成井钻井技术指标对比
Table 5 Comparison of completion and drilling technical indexes between two-section casing program for slim boreholes and typical three-section casing program
井身结构 完井数/口 进尺/m 平均井深/m 钻井周期/d 中完周期/d 完井周期/d 机械钻速/(m·h–1) 小井眼二开 19 91 258 4 803 29.04 4.47 6.09 17.64 典型三开 34 164 442 4 715 42.93 9.93 6.28 12.62 -
[1] 李双贵,于洋,樊艳芳,等. 顺北油气田超深井井身结构优化设计[J]. 石油钻探技术,2020,48(2):6–11. doi: 10.11911/syztjs.2020002 LI Shuanggui, YU Yang, FAN Yanfang, et al. Optimal design of casing programs for ultra-deep wells in the Shunbei Oil and Gas Field[J]. Petroleum Drilling Techniques, 2020, 48(2): 6–11. doi: 10.11911/syztjs.2020002
[2] 刘彪,潘丽娟,王圣明,等. 顺北油气田超深井井身结构系列优化及应用[J]. 石油钻采工艺,2019,41(2):130–136. LIU Biao, PAN Lijuan, WANG Shengming, et al. Casing program optimization and application of ultradeep wells in Shunbei Oil and Gas Field[J]. Oil Drilling & Production Technology, 2019, 41(2): 130–136.
[3] 刘小刚,赵少伟,马英文,等. 渤海油田定向井井身结构优化及应用[J]. 石油钻采工艺,2019,41(4):455–459. LIU Xiaogang, ZHAO Shaowei, MA Yingwen, et al. Optimization of the casing program of directional well and its application in the Bohai Oilfield[J]. Oil Drilling & Production Technology, 2019, 41(4): 455–459.
[4] 乐守群,王进杰,苏前荣,等. 涪陵页岩气田水平井井身结构优化设计[J]. 石油钻探技术,2017,45(1):17–20. LE Shouqun, WANG Jinjie, SU Qianrong, et al. The optimization of casing programs for horizontal wells in the Fuling Shale Gas Field[J]. Petroleum Drilling Techniques, 2017, 45(1): 17–20.
[5] 刘云芳. 平桥地区钻井复杂情况地层压力分析[J]. 江汉石油职工大学学报,2018,31(6):26–28. doi: 10.3969/j.issn.1009-301X.2018.06.007 LIU Yunfang. Formation pressure analysis of drilling complexity in Pingqiao Area[J]. Journal of Jianghan Petroleum University of Staff and Workers, 2018, 31(6): 26–28. doi: 10.3969/j.issn.1009-301X.2018.06.007
[6] 刘阳, 邓建明, 崔国杰, 等. 渤中凹陷19-6构造地层压力随钻精确监测技术[J]. 石油钻采工艺, 2018, 40(增刊1): 125-128. LIU Yang, DENG Jianming, CUI Guojie, et al. Precise detection technology of formation pressure while drilling in BZ19-6 structure of Bozhong Sag[J]. Oil Drilling & Production Technology, 2018, 40(supplement 1): 125-128.
[7] 刘彪,张俊,王居贺,等. 顺北油田含侵入岩区域超深井安全高效钻井技术[J]. 石油钻采工艺,2020,42(2):138–142. LIU Biao, ZHANG Jun, WANG Juhe, et al. Technologies for the safe and efficient drilling of ultradeep wells in the areas with intrusive rocks in the Shunbei Oilfield[J]. Oil Drilling & Production Technology, 2020, 42(2): 138–142.
[8] 刘彪,潘丽娟,易浩,等. 顺北含辉绿岩超深井井身结构优化设计[J]. 石油钻采工艺,2016,38(3):296–301. LIU Biao, PAN Lijuan, YI Hao, et al. Casing program optimization of ultra-deep well with diabase reservoir in Shunbei Block[J]. Oil Drilling & Production Technology, 2016, 38(3): 296–301.
[9] 冯林,母亚军,杨代明,等. 马深1井二开大井眼优快钻井技术[J]. 石油钻采工艺,2016,38(5):577–582. FENG Lin, MU Yajun, YANG Daiming, et al. Big hole of second section of Well Mashen-1 optimized drilling technology[J]. Oil Drilling & Production Technology, 2016, 38(5): 577–582.
[10] 胡大梁,欧彪,何龙,等. 川西海相超深大斜度井井身结构优化及钻井配套技术[J]. 石油钻探技术,2020,48(3):22–28. doi: 10.11911/syztjs.2020053 HU Daliang, OU Biao, HE Long, et al. Casing program optimization and drilling matching technologies for marine ultra-deep highly deviated wells in Western Sichuan[J]. Petroleum Drilling Techniques, 2020, 48(3): 22–28. doi: 10.11911/syztjs.2020053
[11] 林四元,张杰,韩成,等. 东方气田浅部储层大位移水平井钻井关键技术[J]. 石油钻探技术,2019,47(5):17–21. LIN Siyuan, ZHANG Jie, HAN Cheng, et al. Key technology for horizontal well of extended reach drilling in the shallow reservoirs of the Dongfang Gas Field[J]. Petroleum Drilling Techniques, 2019, 47(5): 17–21.
[12] 杨灿,王鹏,饶开波,等. 大港油田页岩油水平井钻井关键技术[J]. 石油钻探技术,2020,48(2):34–41. doi: 10.11911/syztjs.2020036 YANG Can, WANG Peng, RAO Kaibo, et al. Key technologies for drilling horizontal shale oil wells in the Dagang Oilfield[J]. Petroleum Drilling Techniques, 2020, 48(2): 34–41. doi: 10.11911/syztjs.2020036
[13] 路宗羽,赵飞,雷鸣,等. 新疆玛湖油田砂砾岩致密油水平井钻井关键技术[J]. 石油钻探技术,2019,47(2):9–14. doi: 10.11911/syztjs.2019029 LU Zongyu, ZHAO Fei, LEI Ming, et al. Key technologies for drilling horizontal wells in glutenite tight oil reservoirs in the Mahu Oilfield of Xinjiang[J]. Petroleum Drilling Techniques, 2019, 47(2): 9–14. doi: 10.11911/syztjs.2019029
[14] 王敏生,光新军,耿黎东. 页岩油高效开发钻井完井关键技术及发展方向[J]. 石油钻探技术,2019,47(5):1–10. WANG Minsheng, GUANG Xinjun, GENG Lidong. Key drilling/completion technologies and development trends in the efficient development of shale oil[J]. Petroleum Drilling Techniques, 2019, 47(5): 1–10.
[15] 史配铭,肖春学,王建军. 苏里格南部气田大斜度井钻井技术[J]. 石油钻采工艺,2019,41(1):18–22. SHI Peiming, XIAO Chunxue, WANG Jianjun. Drilling technologies used for the highly deviated wells in Southern Sulige Gasfield[J]. Oil Drilling & Production Technology, 2019, 41(1): 18–22.
[16] 聂云飞,朱渊,范萧,等. 自激式涡流控制水力振荡器研制与应用[J]. 石油钻探技术,2019,47(5):74–79. NIE Yunfei, ZHU Yuan, FAN Xiao, et al. Development and application of self-excited vortex control hydraulic oscillator[J]. Petroleum Drilling Techniques, 2019, 47(5): 74–79.
[17] 沈国兵,刘明国,晁文学,等. 涪陵页岩气田三维水平井井眼轨迹控制技术[J]. 石油钻探技术,2016,44(2):10–15. doi: 10.11911/syztjs.201602002 SHEN Guobing, LIU Mingguo, CHAO Wenxue, et al. 3D trajectory control technology for horizontal wells in the Fuling Shale Gas Field[J]. Petroleum Drilling Techniques, 2016, 44(2): 10–15. doi: 10.11911/syztjs.201602002
[18] 胡祖彪,张建卿,王清臣,等. 长庆油田华H50-7井超长水平段钻井液技术[J]. 石油钻探技术,2020,48(4):28–36. doi: 10.11911/syztjs.2020050 HU Zubiao, ZHANG Jianqing, WANG Qingchen, et al. Drilling fluid technology for ultra-long horizontal section of Well Hua H50-7 in the Changqing Oilfield[J]. Petroleum Drilling Techniques, 2020, 48(4): 28–36. doi: 10.11911/syztjs.2020050
-
期刊类型引用(1)
1. 裴旭涛. 化学反应过程中气-液两相流传质性能的数值模拟. 化学工程与装备. 2025(04): 105-107+160 .  百度学术
百度学术
其他类型引用(0)








 下载:
下载: