随着油气勘探开发不断深入，钻井井深逐渐增加，防斜打直成为一大问题^[1-3]。为解决这一问题，自动垂直钻井技术应运而生。目前，自动垂直钻具的控制系统主要有电子控制系统和纯机械控制系统2大类。配备电子控制系统的自动垂直钻具精度高、效率高，但由于存在电子元件，具有不耐高温和易受振动影响等特点，而且损坏后维修成本及日常维护成本很高。配备机械式稳定平台的自动垂直钻具，由于无电子元件，耐高温性能好，成本也相对低廉，具有一定的适应性和应用工况，是深井钻井中防斜打直的较好选择。但由于机械式自动垂直钻具仅依靠机械式稳定平台中的偏重块来完成纠斜，存在纠斜精度相对较低的问题^[4-6]。因此，如何进一步提高纠斜精度，是机械式自动垂直钻具研究的重点与难点。

分析认为，机械式自动垂直钻具的纠斜精度，主要与其控制机构——稳定平台的控制精度有关。稳定平台的控制应精度主要受其结构参数及钻井参数的影响，而具体影响因素及其影响规律目前尚不清楚^[7-10]。为此，笔者利用机械系统多刚体动力学分析软件Adams，分析了影响机械式自动垂直钻具稳定平台性能的因素及其影响规律，以进一步优化机械式自动垂直钻具，提高其纠斜精度。

1.   稳定平台结构及工作原理

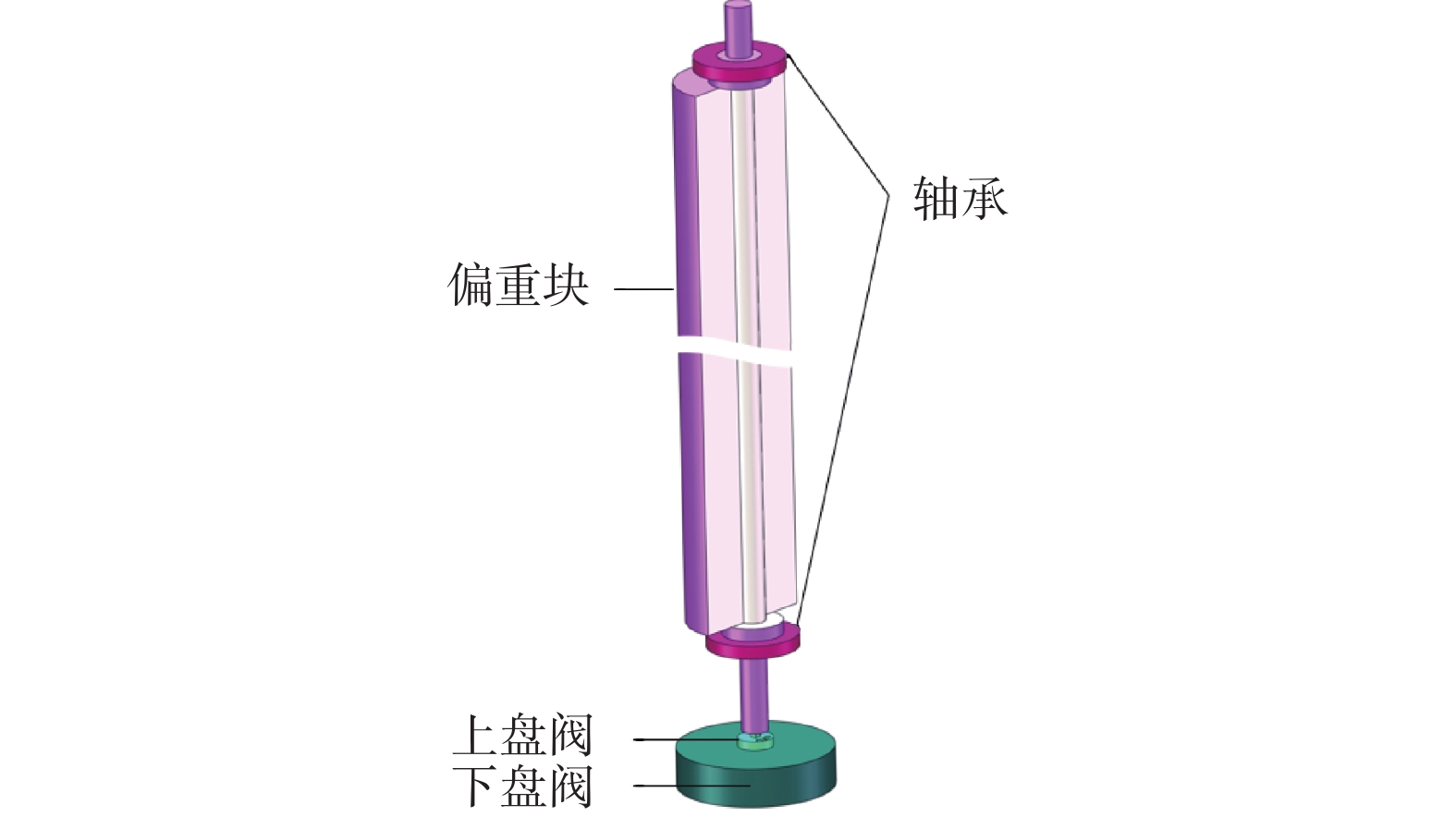
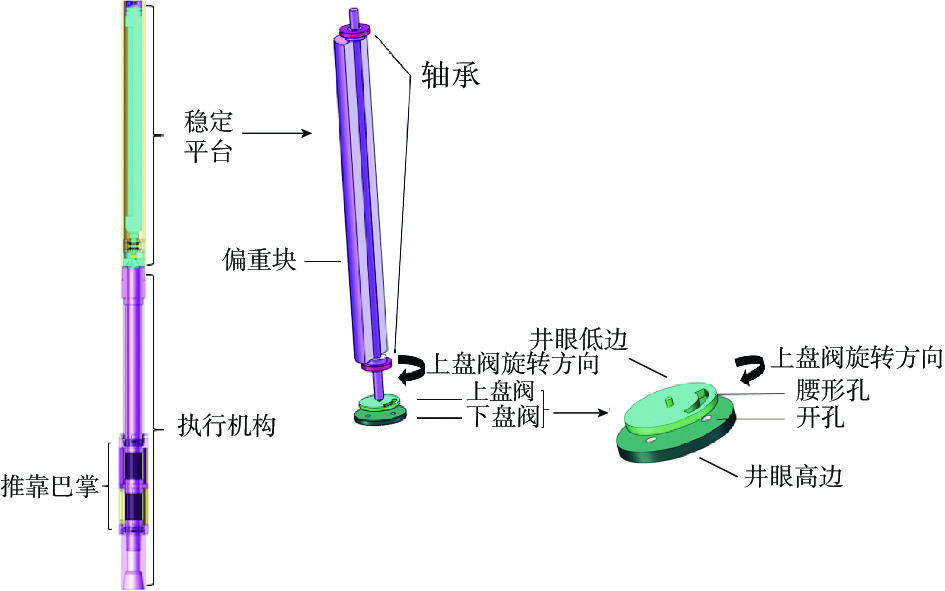
以典型的$\phi$177.8 mm动态推靠机械式自动垂直钻具的稳定平台为例进行介绍和分析。动态推靠机械式自动垂直钻具结构如图1所示，主要由稳定平台和执行机构2部分组成^[11]：稳定平台由偏重块、轴承组、上盘阀、下盘阀和心轴组成；偏重块通过轴承安装在钻具上，可在重力作用下自由转动；偏重块下部与上盘阀通过键连接，保持同步旋转；在上盘阀表面，有一个腰形孔，腰形孔位置与偏重块呈对位分布关系；下盘阀存在多个开孔，这些开孔分别与钻井液流道连通。

图  1  动态推靠机械式自动垂直钻具结构示意

Figure  1.  Structure of mechanical vertical drilling tools with dynamic pushing pistons

下载: 全尺寸图片 幻灯片

该机械式稳定平台的工作原理为：发生井斜时，偏重块在重力作用下偏转并保持在井眼最低边，与偏重块固连的上盘阀也随之同步旋转；上盘阀腰形孔与偏重块呈对位分布关系，所以此时上盘阀腰形孔位于井眼最高边，上盘阀开孔对应的下盘阀位置的开孔（钻井液流道）随之接通，在推靠巴掌两端形成压力差，将巴掌推向井壁；在巴掌推靠力作用下，钻头在井底低边的切削力度加大，井眼轨迹逐渐恢复垂直，达到了纠斜目的。

但由于稳定平台结构间存在摩擦，发生井斜时，受摩擦力作用，偏重块无法到达理想的位置（井眼理想最低边），而是在偏心扭矩和摩擦阻力矩相等的位置（井眼实际最低边）便达到力平衡停止转动，如图2所示。这样会影响稳定平台的性能，降低钻具的纠斜精度。

图  2  摩擦力对偏重块偏转位置的影响示意

Figure  2.  Effect of friction on the deflection position of an eccentric block

下载: 全尺寸图片 幻灯片

图2中，井眼理想最低边和井眼实际最低边之间的夹角$\varphi$称为临界夹角，它是评价机械式稳定平台性能的主要指标。临界夹角越大，意味着偏重块转动所引起下盘阀连接流道的接通区域偏差越大，即流道打开纠斜推靠巴掌的位置偏差越大，稳定平台的纠斜精度越低。由此可知，该偏差是一种固有偏差，与机械式自动垂直钻具的自身结构有关，仅能在一定程度上减小，无法彻底消除。这种偏差除受自身结构参数影响外，还受钻井液性能、外部钻井坏境、孔底振动等外界因素的影响。综合考虑内、外因素影响，将使分析变得更加复杂。因此，为简化分析，选择忽略钻井液性能、浅部地层剧烈振动、深部地层高温高压环境等外界环境因素的影响，重点分析这种固有偏差与钻具自身结构参数之间的关系^[12-14]。

基于上述分析，建立稳定平台临界夹角的表达式^[15]。偏重块处于稳定位置时，其受力如图3所示。

图  3  偏重块受力矩示意

Figure  3.  Torque of the eccentric block

下载: 全尺寸图片 幻灯片

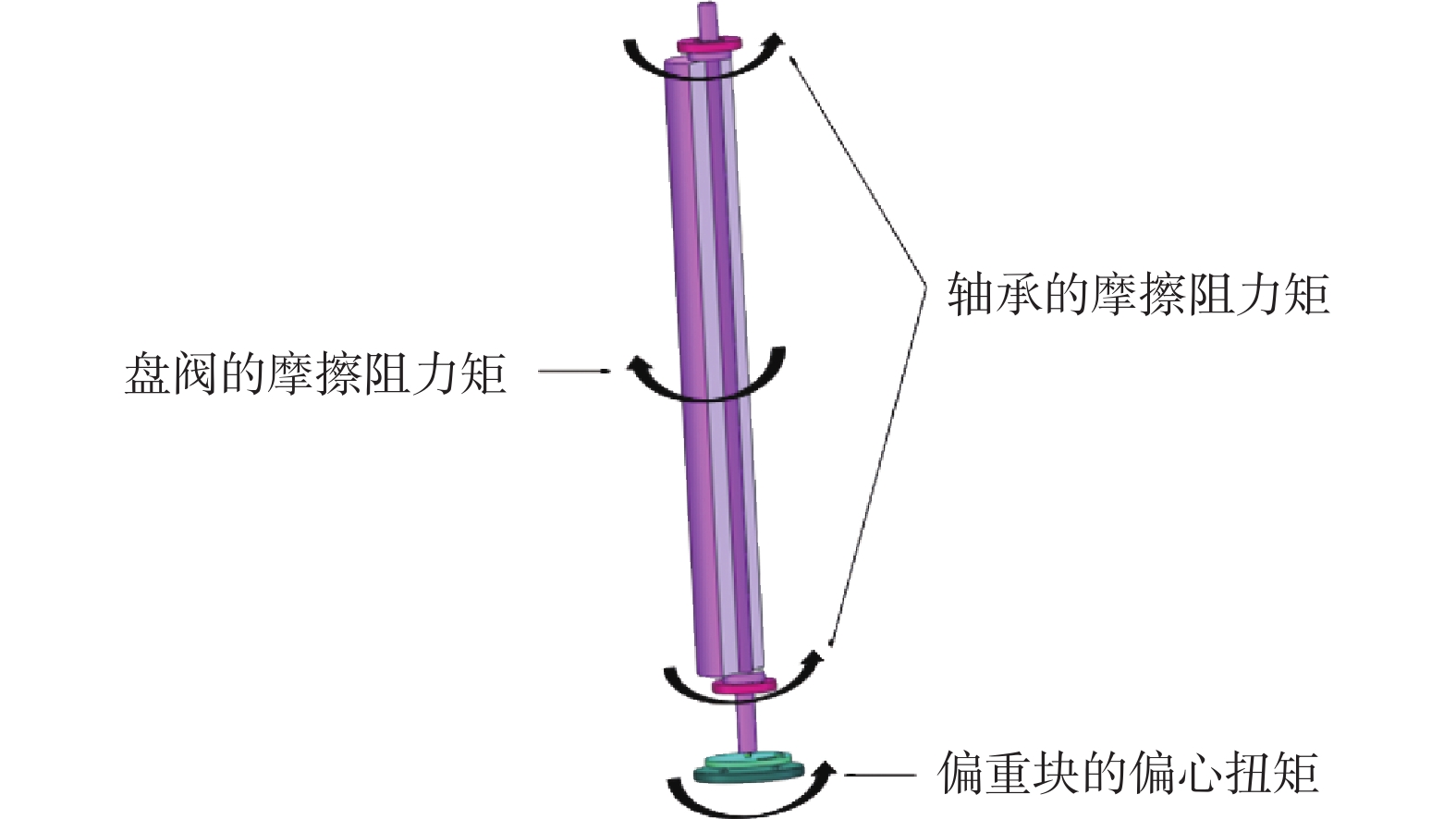
此时，偏重块的偏心扭矩等于轴承摩擦阻力矩和盘阀间的摩擦阻力矩之和，即：

式中：${T}_{\mathrm{E}\mathrm{m}}$为偏重块在一定偏转角度下的最大偏心扭矩，$\mathrm{N} \cdot \mathrm{m}$；${T}_{\mathrm{p}}和{T}_{\mathrm{B}}$分别为盘阀间、轴承的摩擦阻力矩，$\mathrm{N} \cdot \mathrm{m}$ 。

由式（1）可知，盘阀间摩擦阻力矩和轴承摩擦阻力矩都会对稳定平台的临界夹角造成影响。但由于稳定平台中轴承常采用滚动轴承，相对于面面接触的盘阀接触，轴承摩擦阻力矩远小于盘阀间的摩擦阻力矩。为简化分析，笔者忽略轴承间摩擦的影响，将轴承按照理想轴承处理^[14-16]。因此，式（1）可简化为：

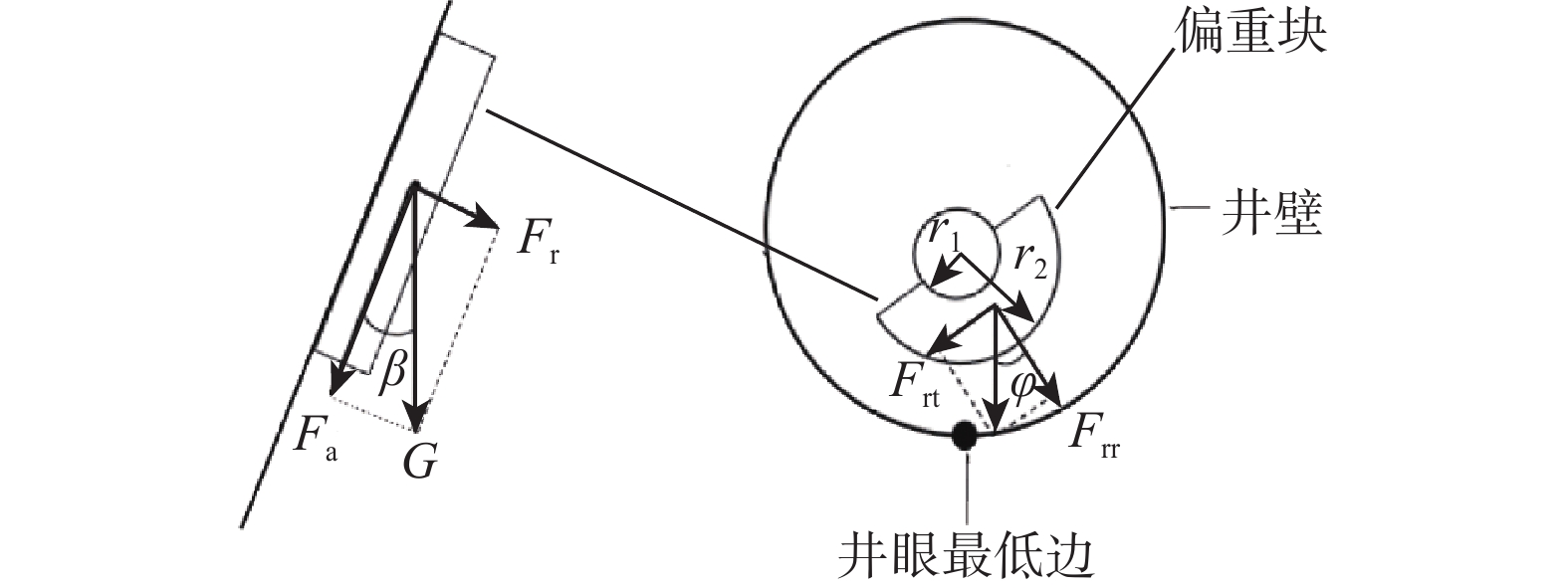
偏重块的横截面采取半圆形设计^[14]，该偏重块在井眼中的位置及受力如图4所示（图4中：$\beta$为偏重块的井斜角，（°）；G为偏重块的重量，N；F_r，F_a分别为偏重块产生的轴向偏心力和径向偏心力，N；F_rt，F_rr分别为F_r在偏重块横截面外缘切向与径向上的分力，N；r₁，r₂分别为偏重块的内外半径，m）。此时，偏心扭矩可表示为：

图  4  偏重块在井眼中的位置及受力示意

Figure  4.  Position and force of the eccentric block in a wellbore

下载: 全尺寸图片 幻灯片

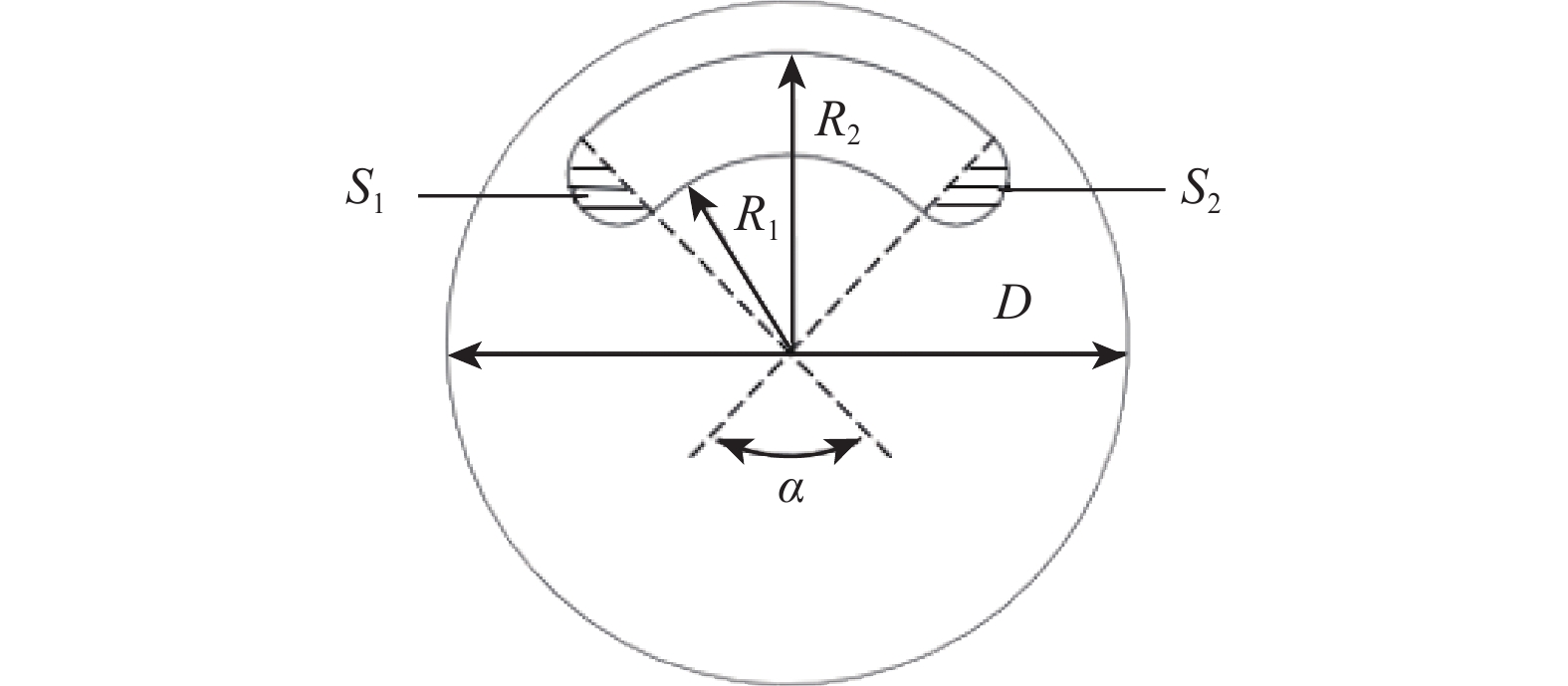
式中：$\rho$为偏重块的密度，$\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}$ ；$g$为重力加速度，$\; \mathrm{m}/\mathrm{s}^2$；$l$为偏重块的长度，m。

上下盘阀转动过程中，在压力差作用下，会产生阻碍偏重块转向井眼最低边的摩擦阻力矩。由于上盘阀存在腰形孔（见图5），将盘阀间摩擦阻力矩分为3部分（分别记为${T}_{\mathrm{p}1}，{T}_{\mathrm{p}2}$和${T}_{\mathrm{p}3}）$分别进行计算。计算时，忽略上盘阀开口部分的阴影面积${S}_{1}$和${S}_{2}\mathrm{。}$$\mathrm{则}{T}_{\mathrm{p}1}，{T}_{\mathrm{p}2}$和${T}_{\mathrm{p}3}$分别为上盘阀半径在$0 < R < {R}_{1}$、${R}_{1} < R < {R}_{2}$和${R}_{2} < R < D/2$范围内的摩擦阻力矩，计算公式为：

式中：${\mu }_{\mathrm{p}}$为盘阀间的动摩擦系数；$p$为上下盘阀间压力差，MPa；${R}_{1}$和${R}_{2}$为上盘阀腰形孔的内外半径，$\mathrm{m}\mathrm{m}$；$D$为上盘阀的外径，$\mathrm{m}\mathrm{m}；\alpha$为上盘阀腰形孔的开口角度，（°）。

图  5  上盘阀结构示意

Figure  5.  Upper disc valve structure

下载: 全尺寸图片 幻灯片

联立式（2）—式（6），可求出偏重块的临界夹角$\varphi$：

由式（7）可知，临界夹角的影响因素主要有：上盘阀外径$D$、腰形孔内半径${R}_{1}$和外半径${R}_{2}$、偏重块密度$\rho$、偏重块长度$l$、偏重块内半径${r}_{1}\mathrm{和}\mathrm{外}\mathrm{半}\mathrm{径}{r}_{2}$、井斜角$\beta$、盘阀间动摩擦系数${\mu }_{\mathrm{p}}$、盘阀间压力差p。

2.   稳定平台动力学模拟

以自行研发的$\phi$177.8 mm机械式自动垂直钻具的稳定平台为例，进行动力学模拟分析。该钻具的关键参数为^[11]：钻具外径177.8 mm，偏重块的密度$7.8\times {10}^{-6}\;\; \mathrm{k}\mathrm{g}/\mathrm{m}{\mathrm{m}}^{3}$，偏重块长度3 000 mm，偏重块内外半径为15和75 mm，上盘阀腰形孔的开口角度$\mathrm{{\text π} }/2，$上盘阀腰形孔的内外半径分别为11和17 mm，上盘阀外径40 mm。为更清楚地了解各因素的具体影响规律，利用Adams软件建立该稳定平台的多刚体动力学模型，利用控制变量法分析该钻具稳定平台的性能。

2.1   模拟模型的建立

利用Solidworks软件建立稳定平台的三维模型，并将其导入Adams软件中对其进行模拟模型的构建。

2.1.1   三维模型

为了提高模拟运算速度，根据前述分析忽略非主要影响因素，对稳定平台结构进行了简化，仅保留上下轴承、偏重块和上下盘阀等关键部件。简化后的稳定平台三维模型如图6所示。

图  6  稳定平台的三维模拟模型

Figure  6.  3D simulation model of a stable platform

下载: 全尺寸图片 幻灯片

2.1.2   Adams模型

为模拟稳定平台的实际工作情况，将建立的三维模型导入Adams，在各运动部件间添加合适的约束，见表1。

表  1  稳定平台部件间约束关系

Table  1.  Constraint relationship between stable platform components

模型名称	构件1	构件2	约束副	放置位置
JOINT_1	下盘阀	大地	转动副	质心
JOINT_2	下盘阀	下部轴承	固定副	质心
JOINT_3	下盘阀	上部轴承	固定副	质心
JOINT_4	上部轴承	偏重块	圆柱副	质心
JOINT_5	下部轴承	偏重块	圆柱副	质心
JOINT_6	下部轴承	偏重块	平面副	质心
JOINT_7	偏重块	上盘阀	移动副	质心

下载: 导出CSV 

| 显示表格

添加约束可最大程度地模拟稳定平台的实际运动状态，偏重块可在重力作用下向井眼低边发生自由转动。上盘阀与偏重块保持同步转动且在轴向存在一定自由行程。上盘阀开口位置与偏重块位置对位分布，开口和偏重块位置分别对应井眼高边和低边位置^[17-18]。

2.1.3   模拟参数

对稳定平台的模拟参数进行选取，选取结果为：上盘阀正压力1 800 N，井斜角3°，驱动角速度573°/s，重力加速度9.8 m/s²，刚度$1.0\times {10}^{5} \; \mathrm{N}/\mathrm{m}\mathrm{m}$，力的非线性指数1.5，阻尼系数500 （N·s）/mm，穿透深度$1.0\times {10}^{-6}$，静摩擦系数0.08，动摩擦系数0.05，静平移速度1 mm/s，摩擦平移速度10 mm/s。

2.2   模拟结果的验证

2.2.1   模拟结果与理论计算结果对比

为了验证模拟模型的准确性，利用上文所列参数，分别采用模拟模型和理论模型（式（7）），计算了井斜角为1.5°、2.0°和3.0°时的临界夹角，结果见表2。

表  2  模拟结果与理论计算结果对比

Table  2.  Comparison of simulation results with theoretical calculations

井斜角/（°）	模拟临界夹角/（°）	理论临界夹角/（°）	相对误差，%
1.5	45.64	46.77	2.476
2.0	32.50	33.12	1.908
3.0	20.97	21.37	1.907

下载: 导出CSV 

| 显示表格

由表2可知，在允许的井斜角范围内，理论计算出临界夹角和模拟得到临界夹角的相对误差平均为2.097%，为可接受的结果。验证结果说明，该模型的计算结果与理论计算结果有较高的吻合度，用其分析稳定平台的性能是可行的。

2.2.2   模拟结果与试验结果对比

为进一步验证模拟模型的准确性，对比了模拟结果与试验结果。该钻具上盘阀的开口角度为120°，推靠巴掌数量为3。

为确保数据的准确性和可记录性，将某一推靠巴掌固定于井眼最高边，自此开始运动并收集数据，得到3个巴掌的推靠力测试曲线，如图7所示^[11]。

图  7  3个巴掌的推靠力测试曲线

Figure  7.  Pushing force test curve of three slaps

下载: 全尺寸图片 幻灯片

由图7可知，偏重块稳定后，位于井眼最高边的推靠巴掌的持续推靠时长可读取。

因此，根据理论持续推靠时长与实际持续推靠时长的关系，即可得出由于存在临界夹角而导致的误差时长，继而得到临界夹角。临界夹角模拟结果与试验结果的对比情况见表3。

表  3  模拟结果与试验结果对比

Table  3.  Comparison of simulation results with experimental results

井斜角/ （°）	转速/ r/min	模拟临界 夹角/（°）	试验临界 夹角/（°）	相对 误差，%
1.6	45	4.63	4.61	4.97
1.6	100	4.63	5.00	7.99
2.5	30	25.40	24.68	2.82
2.5	100	25.40	24.20	4.72

下载: 导出CSV 

| 显示表格

由表3可知，模拟结果与试验结果相差较小，处于可接受范围之内。这也证明，利用建立的Adams模拟模型分析稳定平台的性能具有一定准确性，分析结果具有实际参考价值。

3.   影响稳定平台性能的关键因素

机械式自动垂直钻具稳定平台的性能主要包括控制精度和稳定效率2方面。控制精度可以用稳定平台临界夹角大小来分析，稳定效率可用稳定时间（偏重块从开始转动到稳定在实际井眼最低边位置的时间）来判断。因此，以下采用稳定平台的临界夹角和稳定时间2个指标分析评价影响稳定平台性能的关键因素。

3.1   上盘阀外径

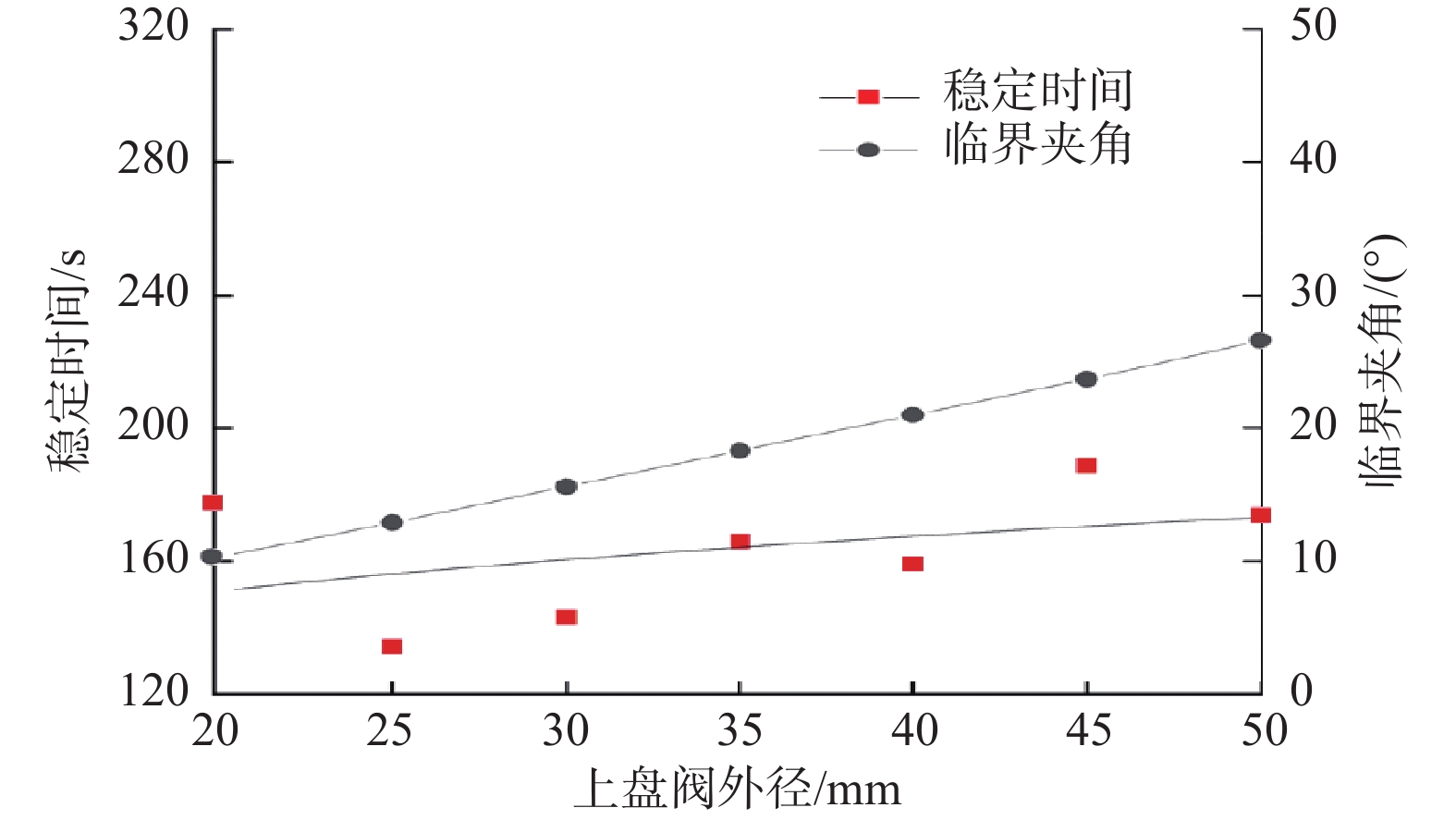
保持其他模型参数、模拟的环境参数以及测量参数不变，模拟稳定平台不同上盘阀外径（在20～50 mm，按等差选取）下的临界夹角及稳定时间，结果如图8所示。

图  8  稳定平台不同上盘阀外径下的临界夹角及稳定时间

Figure  8.  Influence curve of the outer diameter of the upper disc valve on critical angle and stabilization time of the stable platform

下载: 全尺寸图片 幻灯片

从图8可以看出，随着上盘阀外径变大，临界夹角和稳定时间皆呈增长趋势。

临界夹角越大、稳定时间越长，代表稳定平台的性能越差，即机械式稳定平台的控制精度越低，稳定效率越低。由式（4）—式（6）可知，当上盘阀外径变大且其他参数不变的情况下，盘阀间的摩擦阻力矩会变大，因此偏重块需要产生更大的偏心扭矩才可以与盘阀摩擦阻力矩平衡。另外，由式（3）可知，偏心扭矩增大，临界夹角也随之增大。当临界夹角增大的时候，偏重块偏转到井眼实际最低边的角度增大，则花费的时间增长，即稳定时间增长。因此，随着上盘阀外径变大，稳定平台的控制精度和稳定效率变低，机械式自动垂直钻具性能变差。

3.2   腰形孔内外半径

为分析上盘阀腰形孔内外半径对稳定平台性能的影响，保持其他模型参数、模拟环境参数以及测量参数不变，模拟上盘阀腰形孔内外半径4种变化情况下的临界夹角和稳定时间，结果见表4。

表  4  腰形孔内外半径模拟结果

Table  4.  Simulation results of the inner and outer radius of waist hole

情况	内半径/mm	外半径/mm	临界夹角/（°）	稳定时间/s
内半径增大， 外半径不变	11	17	20.944	141.66
	13	17	20.943	136.20
	15	17	20.941	134.81
外半径增大， 内半径不变	11	17	20.944	141.66
	11	18	20.945	159.25
	11	19	20.947	193.63
内外半径同时 增大相同数值	11	17	20.944	141.66
	12	18	20.944	145.66
	13	19	20.944	163.58
内外半径同时 减小相同数值	11	17	20.944	141.66
	10	16	20.944	142.18
	9	15	20.944	151.25

下载: 导出CSV 

| 显示表格

分析表4，可以得出：

1）腰形孔内半径增大、外半径不变（腰形孔变窄）时，临界夹角变小，稳定时间变短。分析认为，腰形孔变窄时，盘阀间的摩擦力矩变小，达到平衡位置所需的偏重块偏心扭矩也变小，所以偏重块要转动到平衡位置需要更小的临界夹角；当临界夹角变小时，偏重块偏转到井眼实际最低边的角度变小，稳定时间变短。随着上盘阀腰形孔变窄，稳定平台的控制精度和稳定效率提高，机械式自动垂直钻具性能变好。

2）腰形孔外半径增大、内半径不变（腰形孔变宽）时，与腰形孔变窄时的原理相同，临界夹角变大，稳定时间变长。稳定平台的控制精度和稳定效率变低，机械式自动垂直钻具性能变差。

3）腰形孔内外半径同时增大（腰形孔在上盘阀的位置沿半径向外移动）相同数值时，临界夹角不变，稳定时间变长。分析认为，腰形孔仅位置改变，大小没有改变，盘阀间的摩擦阻力矩不会改变。随着上盘阀腰形孔位置沿半径方向外移，稳定平台的控制精度不变，稳定效率变低，机械式自动垂直钻具性能变差。

4）腰形孔内外半径同时减小（腰形孔在上盘阀的位置沿半径向内移动）相同数值时，临界夹角不变，稳定时间变长。随着上盘阀腰形孔位置沿半径方向内移，稳定平台的控制精度不变，稳定效率变低，机械式自动垂直钻具性能变差。

3.3   偏重块密度

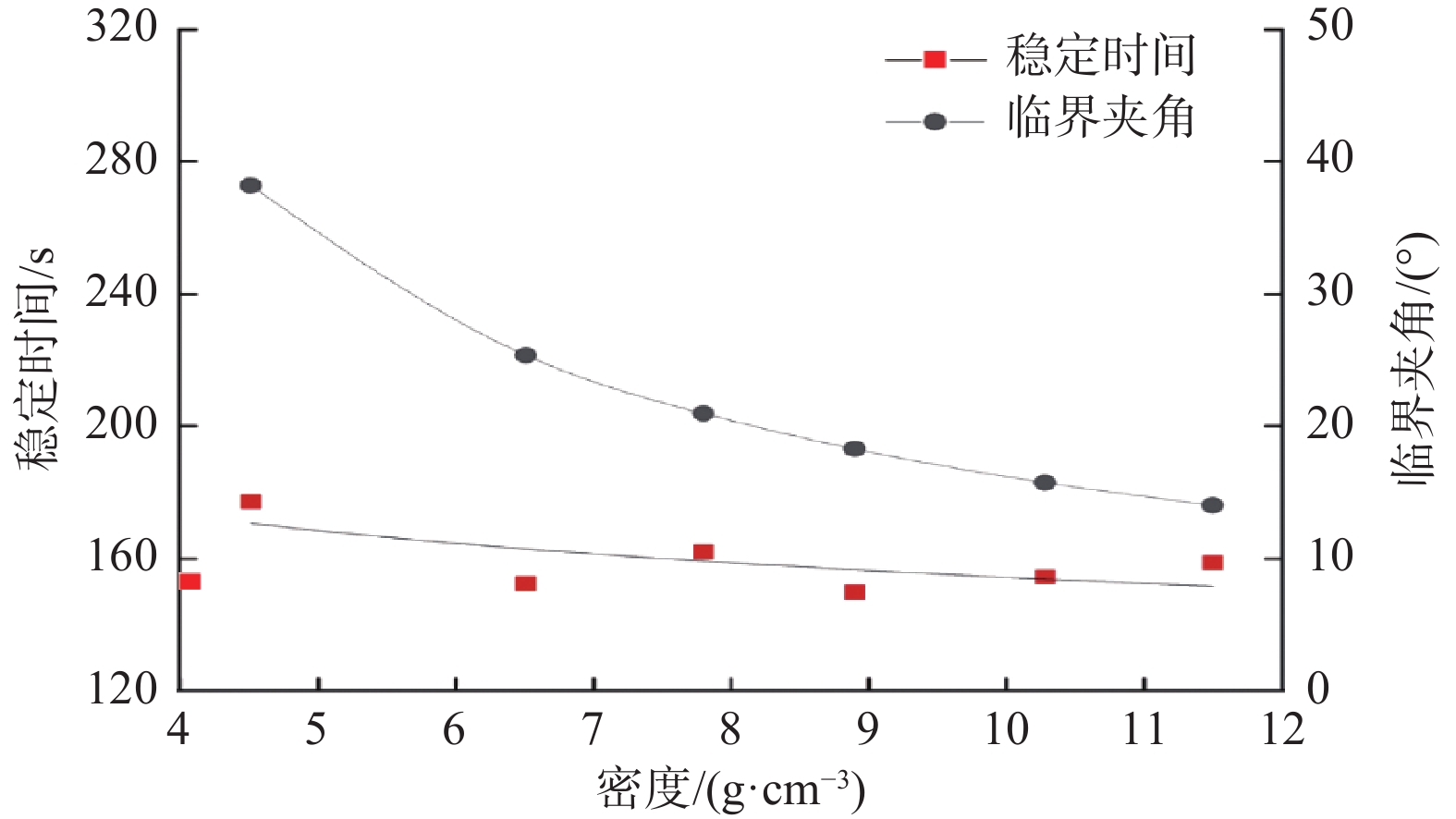
本文研究的偏重块其材质为45#钢。为了研究偏重块密度对稳定平台性能的影响，分别选取了若干密度不同于45#钢且熔点高于井下温度的金属，在保持其他模型参数、模拟环境参数以及测量参数不变的条件下，模拟偏重块所用金属密度对稳定平台性能的影响，结果见图9。各金属的密度和熔点见表5。

表  5  偏重块所用金属的密度和熔点

Table  5.  Densities and melting points for metals of eccentric blocks

金属	密度/（g·cm−3）	熔点/℃
钛	4.51	1 668
锆	6.51	1 855
45#钢	7.80	1 538
钴	8.90	1 495
钼	10.28	2 623
锝	11.50	2 157

下载: 导出CSV 

| 显示表格

图  9  偏重块密度对稳定平台性能的影响

Figure  9.  Influence of eccentric block density on stable platform performance

下载: 全尺寸图片 幻灯片

由图9可知，随着偏重块密度变大，临界夹角变小，稳定时间变短。分析认为，偏重块密度变大，并不会使盘阀间摩擦阻力矩改变，所以在平衡位置要和摩擦阻力矩相等的偏心扭矩也不会改变；不过，偏重块密度变大会导致其偏心扭矩变大。而由式（3）可知，若保持偏心扭矩不变，则需要减小临界夹角。当临界夹角减小时，偏重块偏转到井眼实际最低边的时间缩短，即稳定时间变短。因此，随着偏重块密度增大，稳定平台的控制精度和稳定效率变高，机械式自动垂直钻具性能变好。

3.4   偏重块长度

保持其他模型参数、模拟环境参数以及测量参数不变，模拟偏重块长度对稳定平台性能的影响，结果见图10。

图  10  偏重块长度对稳定平台性能的影响

Figure  10.  Influence of eccentric block length on stable platform performance

下载: 全尺寸图片 幻灯片

从图10可以看出，随着偏重块长度变大，临界夹角变小，稳定时间变短。分析认为，偏重块长度变大，不会导致盘阀间摩擦阻力矩改变，所以在平衡位置要和摩擦阻力矩相等的偏心扭矩也不会改变；不过，偏重块长度变大会导致其偏心扭矩变大。而由式（3）可知，若保持偏心扭矩不变，则需要减小临界夹角。当临界夹角减小时，偏重块偏转到井眼实际最低边需要花费的时间变短，即稳定时间缩短。因此，随着偏重块长度增大，稳定平台的控制精度和稳定效率变高，机械式自动垂直钻具性能变好。

3.5   偏重块内外半径

为了研究偏重块内外半径对机械式稳定平台性能的影响，保持其他模型参数、模拟环境参数以及测量参数不变，模拟稳定平台偏重块内外半径4种变化情况下的临界夹角和稳定时间，结果见表6。

表  6  偏重块内外半径对稳定平台性能影响的模拟结果

Table  6.  Simulation results of influence of the inner and outer radius of eccentric block on stable platform performance

情况	偏重块 内半径/mm	偏重块 外半径/mm	临界 夹角/（°）	稳定 时间/s
内半径增加， 外半径不变	15	75	20.94	164.75
	20	75	21.19	170.00
	25	75	21.61	171.40
外半径增大， 内半径不变	15	75	20.94	164.75
	15	80	17.10	156.07
	15	85	14.18	153.24
内外半径同时 增大相同数值	15	75	20.94	164.75
	20	80	17.27	164.70
	25	85	14.47	161.47
内外半径同时 减小相同数值	15	75	20.94	164.75
	10	70	25.94	168.69
	5	65	33.02	171.47

下载: 导出CSV 

| 显示表格

分析表6，可以得出：

1）偏重块内半径增大、外半径不变（偏重块变薄）时，临界夹角增大，稳定时间变长。偏重块变薄不会导致盘阀间摩擦阻力变化，因此在平衡位置和盘阀间摩擦阻力矩相等的偏心扭矩也不会变化。但由式（3）可知，偏重块变薄时，偏重块偏心扭矩的力矩会变小，为了保持偏心扭矩不变，临界夹角需变大，偏重块偏转到井眼实际最低边花费的时间变长，即稳定时间变长。因此，随着偏重块变薄，稳定平台的控制精度和稳定效率变低，机械式自动垂直钻具性能变差。

2）偏重块外半径增大、内半径不变（偏重块变厚）时，临界夹角变小，稳定时间变短。与偏重块变薄情况下的原因类似，偏重块变厚时，盘阀间摩擦阻力矩不变，但偏心扭矩变大。因此，为了保持偏心扭矩不变，临界夹角将变小，稳定时间随之变短。该情况下，稳定平台的控制精度和稳定效率变高，机械式自动垂直钻具性能变好。

3）偏重块内外半径同时增大相同数值（偏重块整体变粗）时，临界夹角变小，稳定时间变短。偏重块整体变粗不会导致盘阀间摩擦阻力变化，因此在平衡位置和盘阀间摩擦阻力矩相等的偏心扭矩也不会变化。但由式（3）可知，偏重块整体变粗时，偏重块偏心扭矩的力矩会变大，为了保持偏心扭矩不变，临界夹角需变小，偏重块偏转到井眼实际最低边花费的时间变短，即稳定时间变短。因此，随着偏重块整体变粗，稳定平台的控制精度和稳定效率变高，机械式自动垂直钻具性能变好。

4）偏重块内外半径同时减小相同数值（偏重块整体变细）时，临界夹角增大，稳定时间变长。与偏重块整体变粗情况下的原因类似，偏重块整体变细时，盘阀间摩擦阻力矩不变，但偏心扭矩变小。因此，临界夹角变大，稳定时间变长，说明稳定平台的控制精度和稳定效率变低，机械式自动垂直钻具性能变差。

3.6   盘阀间压力差

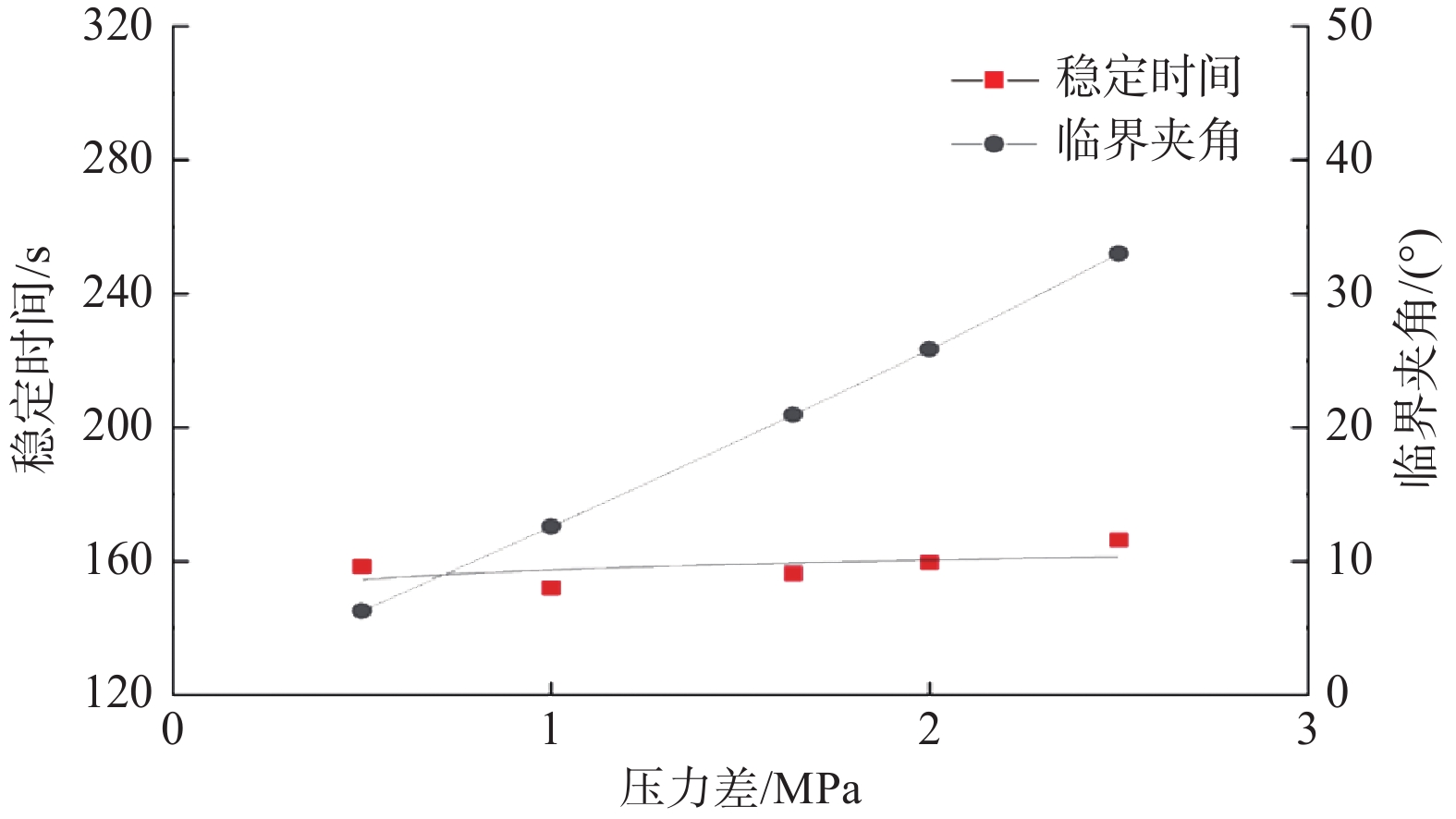
为了研究盘阀间压力差对机械式稳定平台性能的影响，保持其他模型参数、模拟环境参数以及测量参数不变，模拟稳定平台不同盘阀间压力差下的临界夹角和稳定时间，结果如图11所示。

图  11  盘阀间压力差对稳定平台性能的影响

Figure  11.  Curve showing the influence of pressure differences between disc valves on stable platform performance

下载: 全尺寸图片 幻灯片

从图11可以看出，随着盘阀间压力差增大，临界夹角增大，稳定时间小幅增长。分析认为，盘阀间压力差增大，则盘阀间的摩擦力矩增大，偏重块的偏心扭矩也增大，所以由式（3）可知，偏重块要转动到与摩擦阻力矩相等的平衡位置需要更大的临界夹角；而当临界夹角增大时，偏重块偏转到井眼实际最低边花费的时间增长，即稳定时间增长。因此，随着盘阀间压力差增大，稳定平台的控制精度和稳定效率变低，机械式自动垂直钻具性能变差。

3.7   井斜角

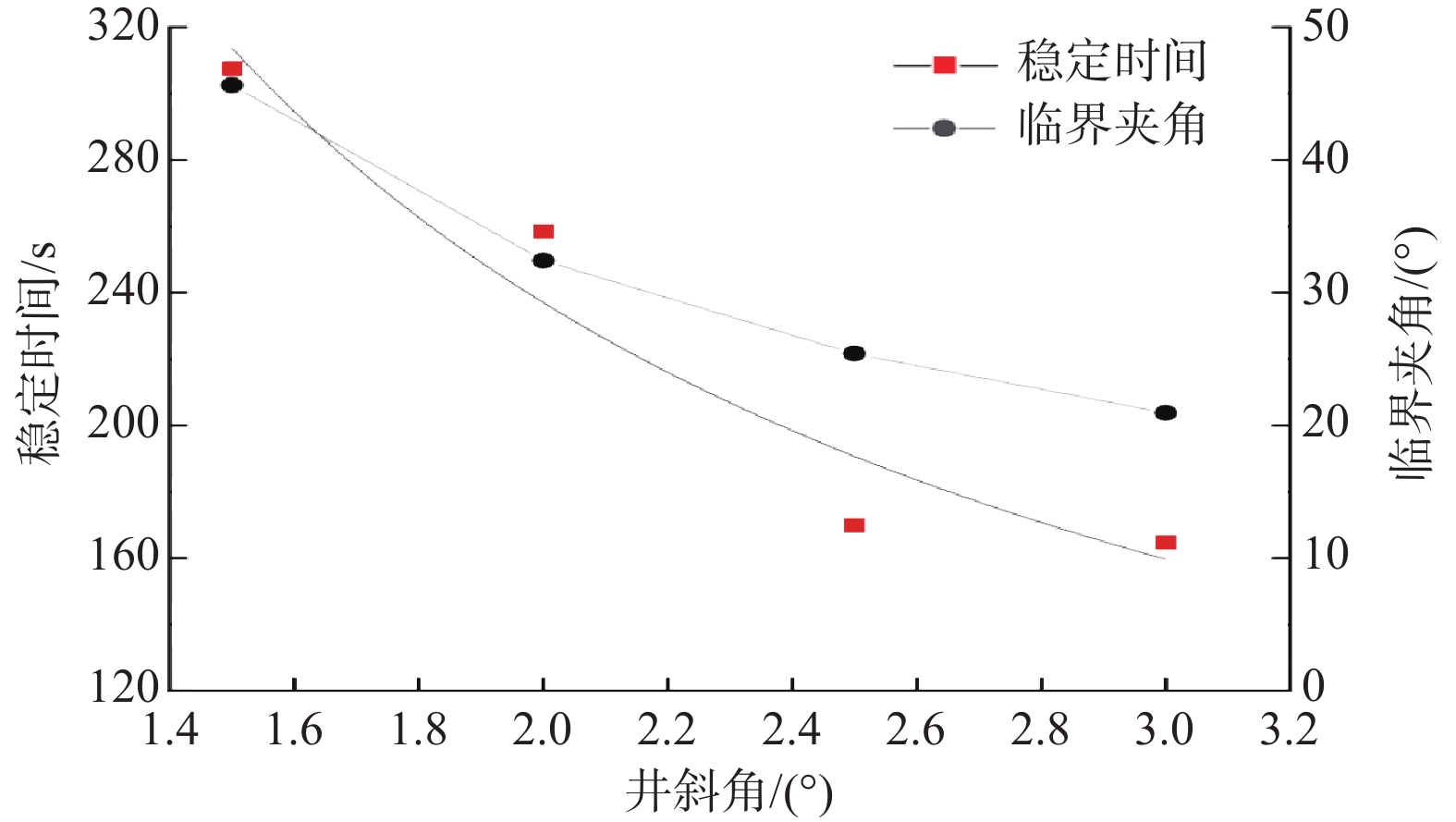
为了研究井斜角对机械式稳定平台性能的影响，保持模型参数、其他模拟环境参数以及测量参数不变，模拟稳定平台不同井斜角下的临界夹角和稳定时间，结果如图12所示。

图  12  井斜角对稳定平台性能的影响曲线

Figure  12.  Curve showing the influence of the inclination angle on stable platform performance

下载: 全尺寸图片 幻灯片

从图12可以看出，随着井斜角增大，临界夹角减小，稳定时间增长。分析认为，仅改变井斜角时，盘阀间的摩擦阻力矩不会变化，偏重块的偏心扭矩也保持不变；当井斜角变大时，由式（3）可知，只有临界夹角变小，偏重块的偏心扭矩才可以保持不变；而临界夹角变小，则偏重块偏转到井眼实际最低边花费的时间变，即稳定响应变快。因此，随着井斜角增大，稳定平台的控制精度和稳定效率变高，机械式自动垂直钻具性能变好。

3.8   盘阀间动摩擦系数

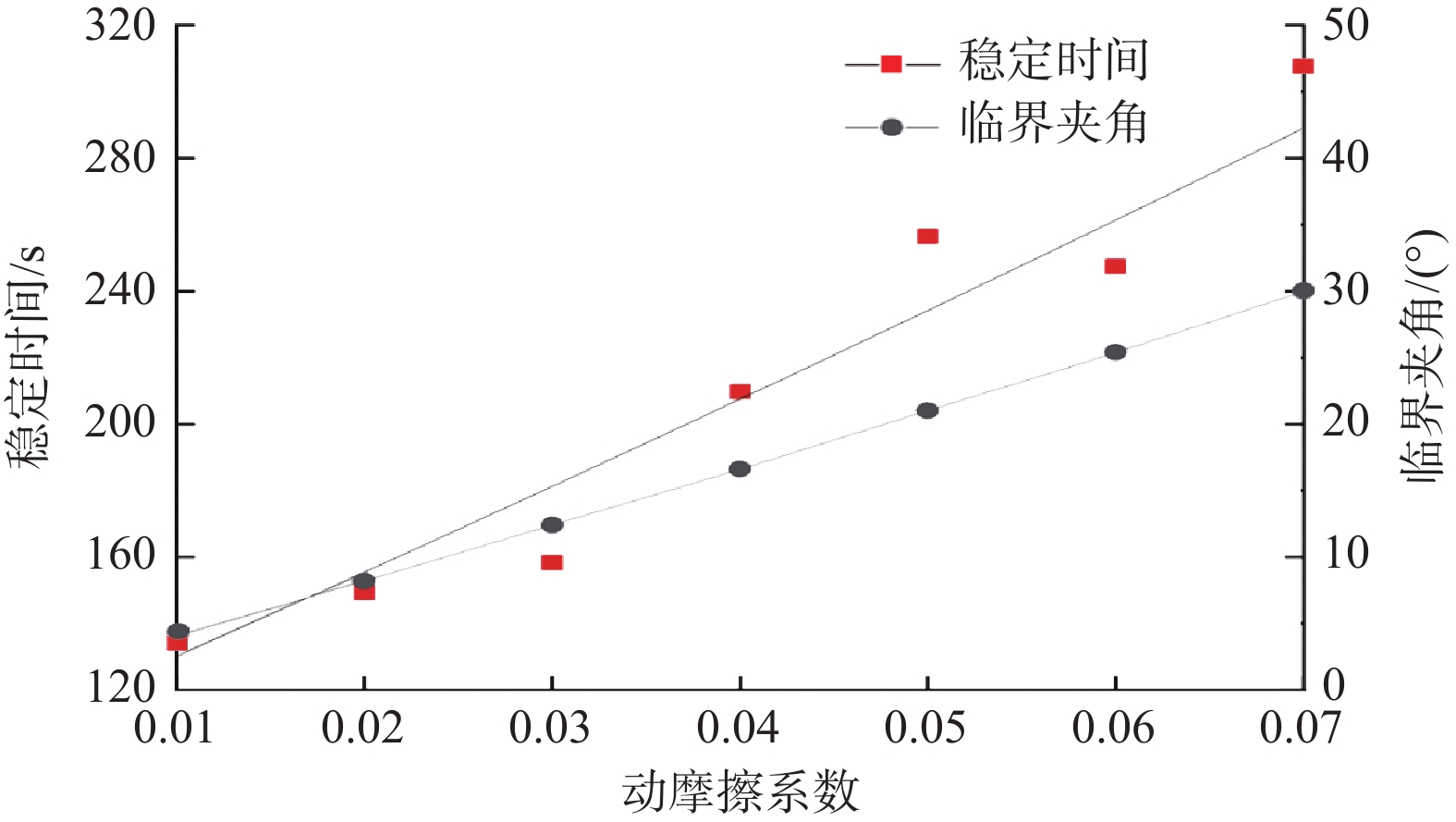
为了研究盘阀间动摩擦系数对机械式稳定平台性能的影响，保持模型参数、模拟环境参数和其他测量参数不变，模拟稳定平台不同盘阀间动摩擦系数下的临界夹角和稳定时间，结果如图13所示。

图  13  盘阀间动摩擦系数对稳定平台性能的影响

Figure  13.  Curve showing the influence of the dynamic friction coefficient between disc valves on stable platform performance

下载: 全尺寸图片 幻灯片

从图13可以看出，随着动摩擦系数变大，稳定平台的临界角变大，稳定时间变长。分析认为，盘阀间动摩擦系数逐渐变大时，盘阀间摩擦阻力矩也随之变大，偏重块需要产生更大的偏心扭矩才可以与盘阀摩擦阻力矩相等；由式（3）可知，偏心扭矩增大则临界夹角增大，当临界夹角增大时，偏重块偏转到井眼实际最低边花费的时间增长，即稳定时间增长。因此，随着盘阀间动摩擦系数增大，稳定平台的控制精度和稳定效率变低，机械式自动垂直钻具性能变差。

3.9   模拟结果综合分析

综合上述模拟分析结果可知，上盘阀外径D、偏重块密度$\rho$、偏重块长度$l$、盘阀间压力差$p$、井斜角$\beta$和盘阀间动摩擦系数${\mu }_{\mathrm{p}}$对工具纠斜精度的影响较大，腰形孔内外半径${R}_{1}$和${R}_{2}$、偏重块长度$l$、偏重块内外半径${r}_{1}$和${r}_{2}$、井斜角$\beta$、盘阀间动摩擦系数${\mu }_{\mathrm{p}}$对工具纠斜效率的影响较大。但井斜角无法人为改变，故不再讨论，其他参数对稳定平台性能的影响见表7。

表  7  优化机械式稳定平台时参数变化趋势

Table  7.  Parameter changing trend when optimizing a mechanical stable platform

参数	参数优化方向		参数优化建议
	控制精度提高	稳定效率提高
上盘阀外径	减小		尽可能减小
腰形孔外半径		减小	尽可能减小
偏重块密度	增大		8～10 g⁄cm3
偏重块长度	增大	增大	3 000～4 000 mm
偏重块内半径	减小		7.5～12.5 mm
偏重块外半径	减小		67.5～72.5 mm
盘阀间压力差	减小		尽可能减小
盘阀间动摩擦系数	减小	减小	尽可能减小
注：表中空白部分表示参数对稳定平台控制精度或稳定效率的影响较小。

下载: 导出CSV 

| 显示表格

由表7可得以下结论：

1）可同时提高稳定平台控制精度与稳定效率的参数为偏重块长度和盘阀间动摩擦系数：偏重块长度越大，稳定平台性能越优，但偏重块长度超过4 000 mm后，控制精度和稳定效率的提高幅度很小，因此偏重块长度选在3 000～4 000 mm为宜；盘阀间动摩擦系数减小，稳定平台性能会提升，所以尽量减小。

2）仅影响稳定平台控制精度的参数有盘阀间压力差、偏重块内（外）半径、偏重块密度、上盘阀外径。即在控制精度不满足使用要求时，通过调整以上参数，可在保证现有稳定效率基础上实现控制精度的提升。按照影响程度排序为：盘阀间压力差＞偏重块内（外）半径＞偏重块密度＞上盘阀外径。

3）仅影响稳定效率的参数为腰形孔外半径。即在稳定效率不满足使用要求时，可通过调整腰形孔外半径，实现在提升稳定效率的同时，保证工具现有控制精度。

4.   结论与建议

1）根据动态推靠机械式自动垂直钻具的结构及其工作原理，建立了该钻具稳定平台偏重块的临界夹角分析模型，确定了影响机械式稳定平台纠斜能力的因素。

2）通过理论计算及模拟计算，分析了各因素对稳定平台纠斜精度及纠斜效率2个主要工作性能的影响，总结出了各因素的影响规律。其中，上盘阀外径、偏重块密度、偏重块长度、偏重块内外半径、盘阀间压力差、井斜角和盘阀间动摩擦系数对工具纠斜精度的影响较大；腰形孔内外半径、偏重块长度、偏重块内外半径、井斜角、盘阀间动摩擦系数对钻具纠斜效率的影响较大。

3）偏重块长度和盘阀间动摩擦系数可同时影响稳定平台的控制精度和稳定效率，在后续的工具优化设计中应优先考虑。

4）影响机械式稳定平台纠斜性能的因素众多，影响规律差异性较大，后续在机械式稳定平台优化设计中，可先根据本文提出的结构参数优化建议对设计参数进行筛选后再开展多因素耦合分析，综合考虑各因素对钻具纠斜精度和纠斜效率所产生的影响，最大程度地简化分析过程，进而达到优化稳定平台性能、提高自动垂直钻井工具纠斜能力的目的。