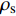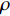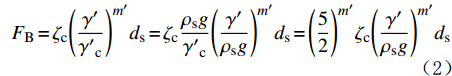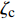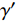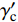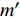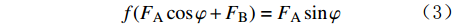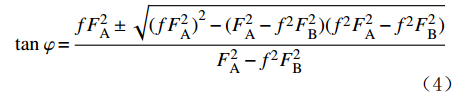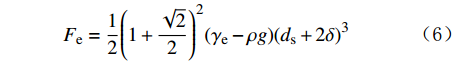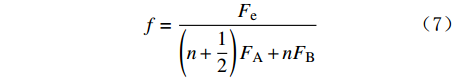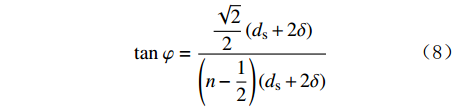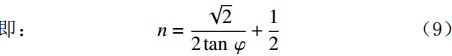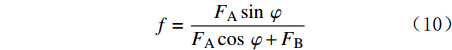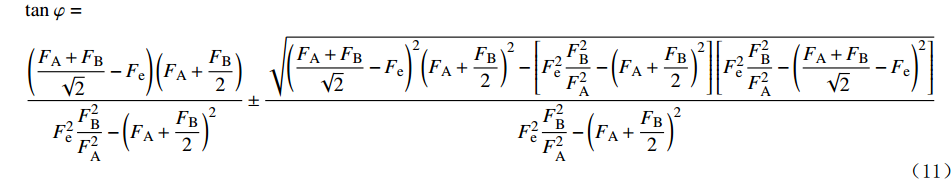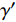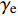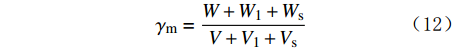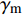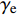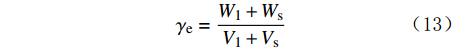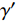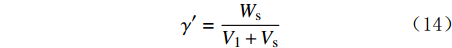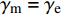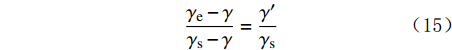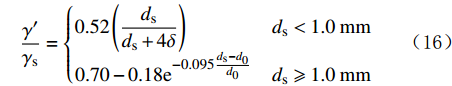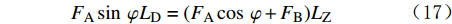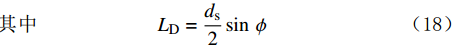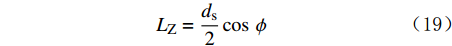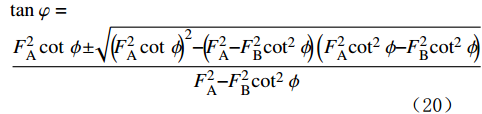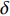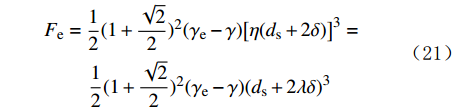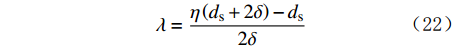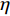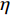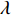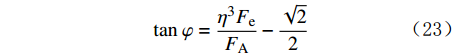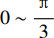The Establishment and Correction of a Prediction Model for the Repose Angle of a Cuttings Bed in Highly Deviated Well Interval
-
摘要:
大斜度井段岩屑床容易失稳或整体下滑迅速堆积成砂塞,而岩屑床失稳位置不好预测。为解决该问题,分析了岩屑床在大斜度井段的受力情况,建立了岩屑床休止角预测模型。基于楔入堆积模型,通过分析平均岩屑床面颗粒滚动与滑动时的受力情况,结合泥沙沉积学中的容重概念,建立了岩屑床休止角预测模型;同时,通过岩屑在不同浓度聚丙烯酰胺聚合物(PAM)溶液中的休止角测量试验,对该预测模型进行了修正。不同浓度聚丙烯酰胺聚合物溶液中岩屑床休止角的试验值分别为26.9°、27.5°、29.7°和30.2°,由滑动休止角预测模型得到滑动休止角的理论值分别为24.2°、25.8°、27.1°和28.5°,而滚动休止角理论值也不超过30°,理论值相较于试验值偏于保守,但按理论值可保证钻井作业安全。研究认为,建立和修正后的大斜度井段岩屑床休止角预测模型,其预测结果较为可靠,可在确定井眼清洁工具有效位置、判断井下故障位置时应用和参考。
Abstract:The cuttings bed in the highly-deviated well interval of a horizontal well can easily cause instability or overall sliding and successive rapid sand plug accumulation, while the instability section of cuttings bed is difficult to predict. In order to solve this problem, the force balance of the cuttings bed in a highly-deviated well interval was analyzed, and the prediction method for the repose angle of cuttings bed was studied. Based on the wedging accumulation model in sedimentology, the prediction model for the repose angle of cuttings bed was established by analyzing the force conditions of particle rolling and sliding of the average cuttings bed surface and combining it with the bulk density concept. At the same time, the prediction model was corrected accordingly by measuring the repose angle of cuttings bed in polyacrylamide polymer (PAM) solutions with various concentrations. The test values of the repose angles in those polyacrylamide polymer solutions were 26.9°, 27.5°, 29.7° and 30.2°, respectively, and the theoretical values obtained from the sliding repose angle prediction model were 24.2°, 25.8°, 27.1° and 28.5°, respectively. The theoretical value is more conservative compared with the tested one, whereas the theoretical value can ensure safe drilling. According to this research, the established and corrected prediction model for the repose angle of cuttings bed in a highly-deviated well interval can render reliable prediction results, and it could be applied and provide references in determining the effective section of the wellbore cleaning tools and the location of downhole failures.
-
水平井、大位移井能够有效提高油气采收率,因而被广泛应用于陆地及海上油气开采。但在钻进大斜度井段和水平段时,岩屑容易堆积形成岩屑床,尤其是在接单根或者检修设备等长时间停泵的工况下,岩屑受重力作用大量沉积在大斜度井段,容易发生岩屑床整体下滑而掩埋井眼,造成沉砂卡钻等井下故障。因此,有必要研究大斜度井段岩屑床形成后井眼内的静态平衡条件,即岩屑床的休止角。认识岩屑床休止角有助于预测沉砂卡钻位置,然后采取有效措施提高携岩效率。
目前,关于固体颗粒休止角的研究以试验为主[1–8],理论研究不够系统[9–10]。根据已有研究结果可知,天然砂、石块、煤屑等粒径较大散体颗粒的休止角随粒径增大而增大[11–12],煤粉、硅砂、纯碱和石灰石等粒径较小颗粒休止角的变化正好相反,粒径越小,它们的休止角越大[13–15]。固体颗粒休止角的研究成果已广泛应用于泥沙运动学、地质安全等领域,并且在这些领域通过试验手段得到了一些具有应用价值的经验公式。相比其他领域,钻井工程中的岩屑床休止角问题有一定的特殊性,例如,由于钻井液中添加了膨润土及地层中存在一定量的黏性介质,使岩屑颗粒在大斜度井段沉积后并不像散体颗粒,而是更接近于堆积的黏性颗粒。但是,关于钻井工程中岩屑休止角的问题,截至目前尚缺乏全面、系统的研究。为此,笔者视岩屑颗粒为黏性体,考虑岩屑堆积后的黏结力,建立了岩屑床休止角预测模型,通过试验修正了该模型中的相关经验系数,以期得到较为准确的水平井、大位移井岩屑床休止角,为选用井眼清洁工具提供理论依据,为快速确定井底卡钻位置提供帮助。
1. 岩屑床休止角预测模型的建立
对于颗粒休止角的定义,当前主要有2种观点[16]:一种观点认为,当颗粒由运动状态转变为静止状态时,其稳定堆积所形成的斜面与水平面间的夹角为休止角;另一种观点认为,颗粒在坡面上将要滑动或者开始滑动时,坡面与水平面的夹角为休止角。基于岩屑在大斜度井段沉积的实际情况,笔者认为第二种观点更正确,即在大斜度井段钻进时,沿井眼轴线方向,颗粒所受摩擦力与重力的分力相等时,岩屑所在井段与水平方向的夹角称为岩屑床休止角,与岩屑床休止角互余的井斜角为休止井斜角。
1.1 颗粒在岩屑床面滑动失衡时的受力模型
岩屑颗粒在平均岩屑床面主要受范德华力、静电力、内摩擦力、黏结力和浮重等作用力。但是:1)岩屑颗粒粒径相对较大;2)当前对于颗粒堆积状态下颗粒间相互作用力的研究尚不完善;3)相比岩屑浮重对颗粒的作用,静电力等粒间作用力对岩屑的作用较小。考虑到以上因素,忽略范德华力、静电力等粒间作用力。在此基础上,分析岩屑颗粒在平均岩屑床面下滑时的力学平衡问题,结果见图1(图1中:Ff为粒子所受摩擦力,N;FA为颗粒的浮重,N;FB为黏结力,N;
φ 为岩屑床休止角,(°);α为休止井斜角,(°))。颗粒的浮重可表示为:
FA=π6(ρs−ρ)gd3s (1) 式中:
ρs 为岩屑颗粒密度,kg/m3;ρ 为钻井液密度,kg/m3;g为重力加速度,m/s2;ds为岩屑颗粒直径,m。颗粒受到的平均岩屑床面的黏结力采用文献[17]中的公式计算,对其进行适当简化,可表示为:
FB=ζc(γ′γ′c)m′ds=ζcρsgγ′c(γ′ρsg)m′ds=(52)m′ζc(γ′ρsg)m′ds (2) 式中:
ζc 为岩屑稳定干容重的黏结力系数,取经验值4.654×10–5 N/m3;γ′ 为岩屑干容重,N/m3;γ′c 为岩屑稳定干容重,N/m3;m′ 为无量纲常数,取经验值10。根据图1可以得到颗粒在x方向的力学平衡方程:
f(FAcosφ+FB)=FAsinφ (3) 对式(3)进行整理,可得:
tanφ=fF2A±√(fF2A)2−(F2A−f2F2B)(f2F2A−f2F2B)F2A−f2F2B (4) 式中:f为平均岩屑床面摩擦系数。
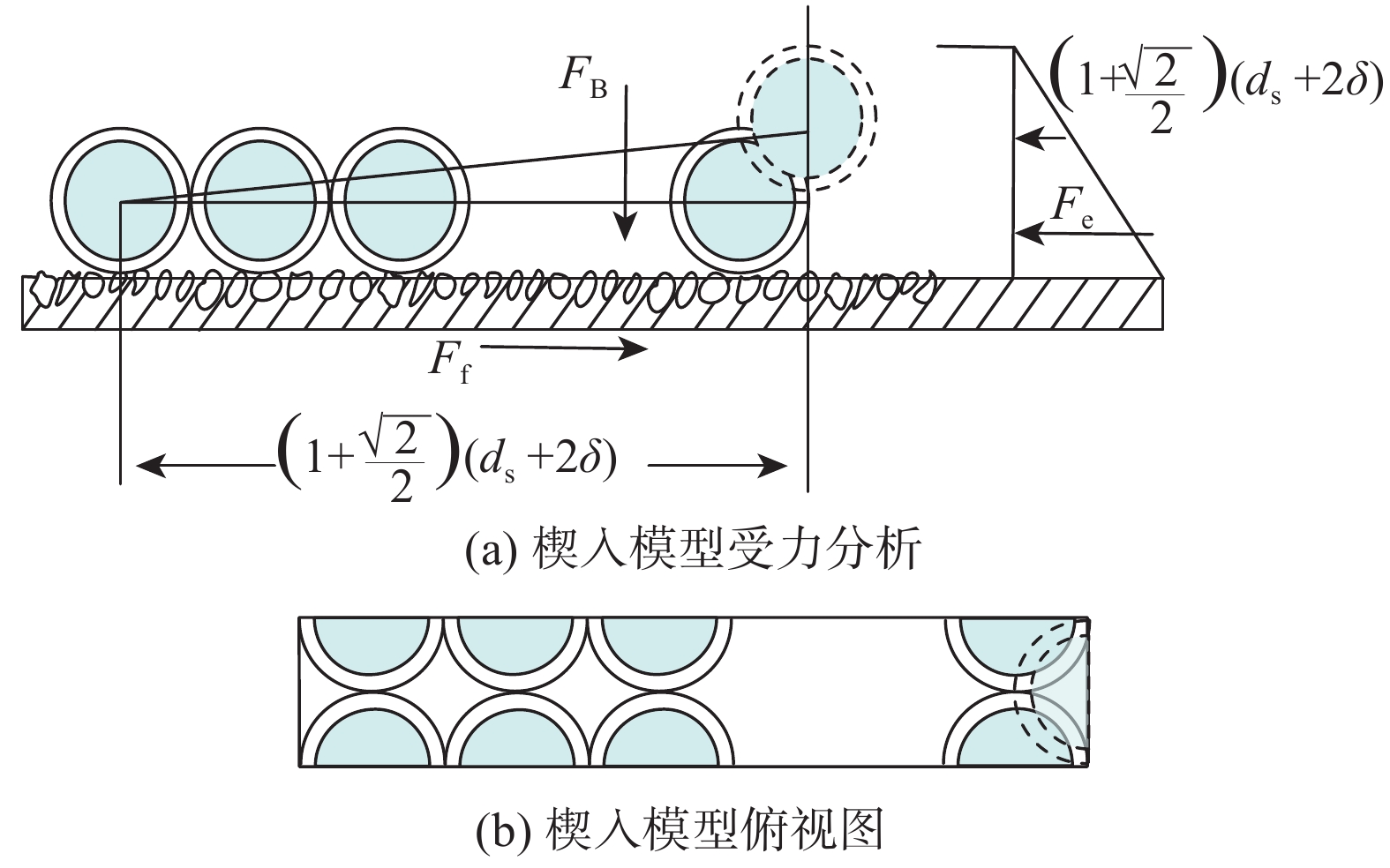
式(4)中f为未知数,需要求解。基于楔入堆积模式[18],只考虑两层岩屑颗粒,取宽度为ds+2δ、长度为n(ds+2δ)的岩屑脱离体进行分析(脱离体主要受浮重、黏结力和侧向压力),其受力情况如图2所示(图2中:n为位于第一层单位宽度内的粒子数;δ为颗粒表面液膜厚度,一般取0.001~0.010 mm;Fe为脱离体所有粒子的总侧向压力,N)。
对脱离体所有粒子在水平方向进行受力分析,则粒子所受摩擦力为:
Ff=[(n+12)FA+nFB]f (5) 总侧向压力为:
Fe=12(1+√22)2(γe−ρg)(ds+2δ)3 (6) 式中:
γe 为岩屑的湿容重,N/m3。当颗粒处在临界状态时受力达到平衡,
Ff−Fe=0 。因此有:f=Fe(n+12)FA+nFB (7) 此时,n为未知数,由图2(a)中的几何关系可得:
tanφ=√22(ds+2δ)(n−12)(ds+2δ) (8) 即:n=√22tanφ+12 (9) 由式(3)可得:
f=FAsinφFAcosφ+FB (10) 此时,式(4)可变为:
tanφ=(FA+FB√2−Fe)(FA+FB2)F2eF2BF2A−(FA+FB2)2±√(FA+FB√2−Fe)2(FA+FB2)2−[F2eF2BF2A−(FA+FB2)2][F2eF2BF2A−(FA+FB√2−Fe)2]F2eF2BF2A−(FA+FB2)2 (11) 式(2)和式(6)中的
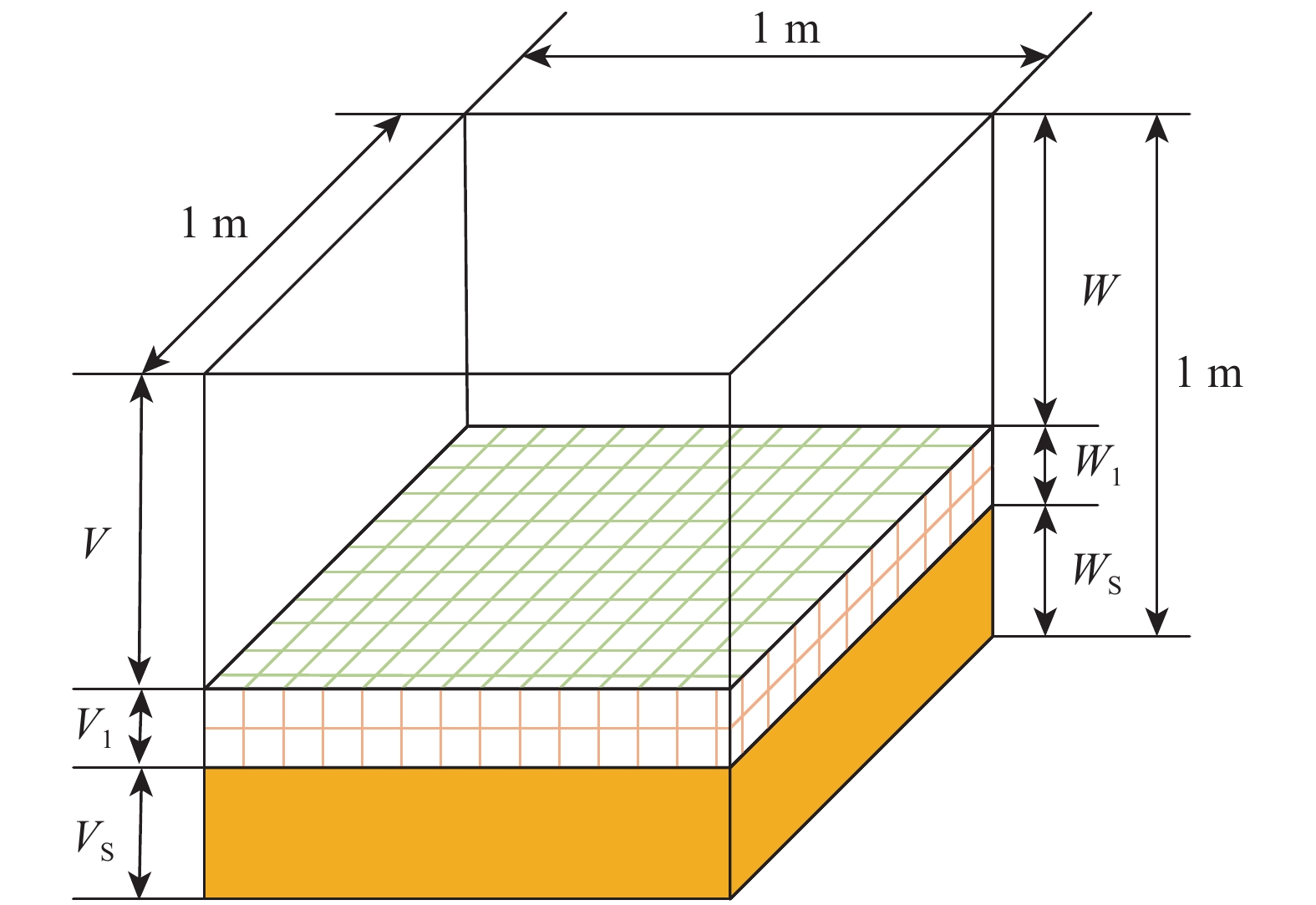
γ′ 和γe 依然未知。为此,根据土力学关系,设想在单位体积浑浊钻井液中,岩屑沉积后分为纯钻井液、有空隙的稳定岩屑和无空隙的密实岩屑,如图3所示(图3中:Ws为最下层沉积后无孔隙的密实岩屑重量,N;Vs为最下层沉积后无孔隙的密实岩屑体积,m3;W为最上层纯钻井液的重量,N;V为最上层纯钻井液的体积,m3;W1为中间部分自然沉积后岩屑空隙中钻井液的重量,N;V1为中间部分自然沉积后岩屑空隙中钻井液的体积,m3)。浑浊钻井液容重可表示为浑浊钻井液重量与浑浊钻井液体积之比,即:
γm=W+W1+WsV+V1+Vs (12) 式中:
γm 为浑浊钻井液容重,N/m3。岩屑的湿容重
γe 为:γe=W1+WsV1+Vs (13) 岩屑的干容重
γ′ 为:γ′=WsV1+Vs (14) 停钻后,岩屑开始沉降。当岩屑在大斜度井段的浓度达到最大时,即最上层液体的体积趋近于0,最上层纯钻井液的重量也趋近于0,此时
γm=γe 。则有:γe−γγs−γ=γ′γs (15) γ′γs={0.52(dsds+4δ)ds<1.0mm0.70−0.18e−0.095ds−d0d0ds⩾ (16) 式中:d0为参考粒径,取1.0 mm。
综上所述,岩屑颗粒滑动时的休止角
\varphi 可求。1.2 颗粒在岩屑床面滚动失衡时的受力模型
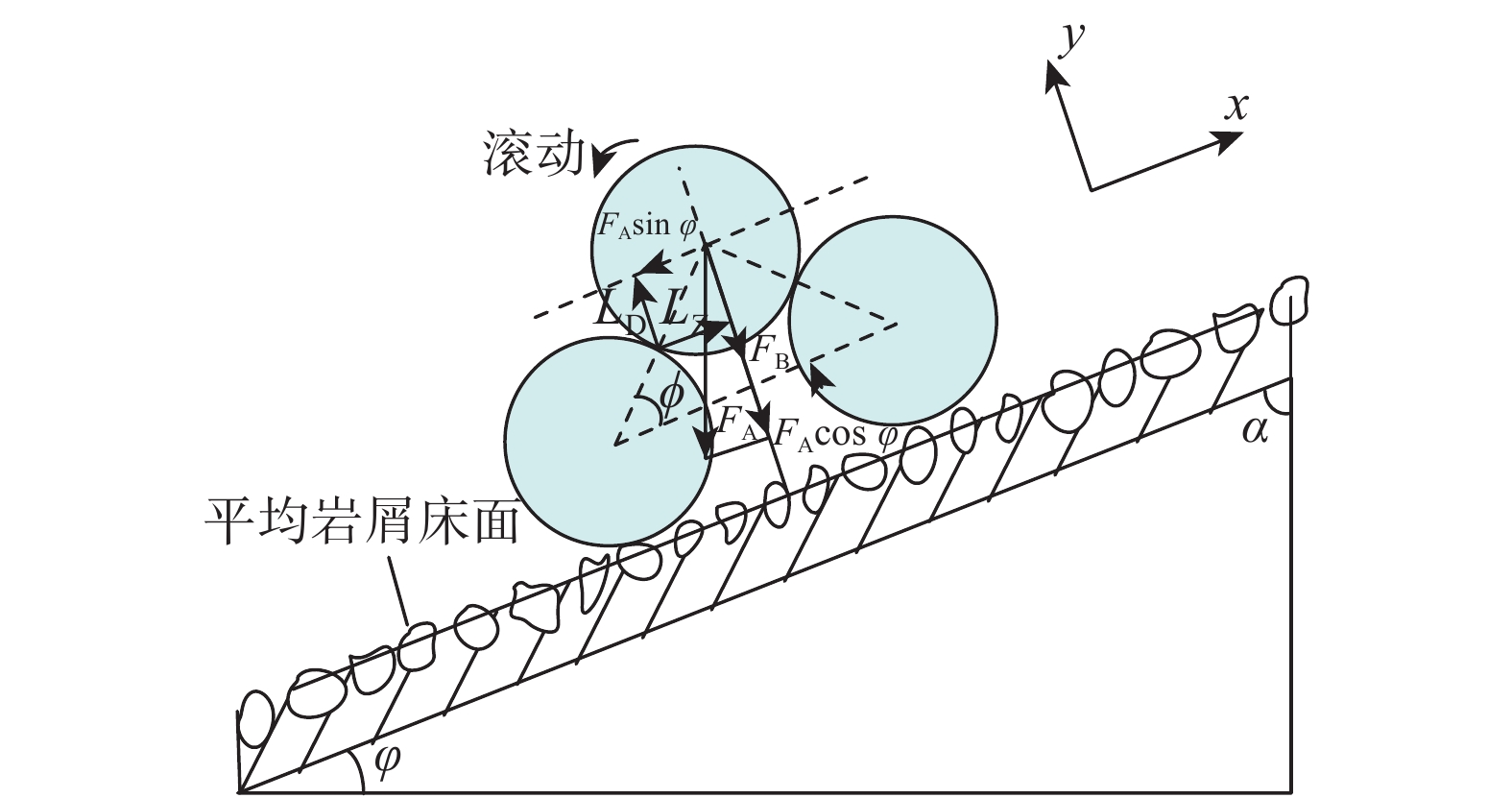
颗粒在平均岩屑床面向下滚动时的受力如图4所示(图4中:LD为动力对应的动力臂,m;LZ为阻力所对应的阻力臂,m;ϕ为颗粒堆积夹角,(°))。
根据图4,颗粒在x方向向下滚动时的力学平衡方程为:
{F_{\rm{A}}}\sin \;\varphi {L_{\rm{D}}} = ({F_{\rm{A}}}\cos\; \varphi + {F_{\rm{B}}}){L_{\rm{Z}}} (17) \!{\text{其中}}\qquad\qquad\qquad {L_{\rm{D}}} = \frac{{{d_{\rm{s}}}}}{{\rm{2}}}\sin\; \phi \qquad\qquad (18) {L_{\rm{Z}}} = \frac{{{d_{\rm{s}}}}}{{\rm{2}}}\cos\; \phi \quad\quad (19) 由此可得岩屑颗粒滑动时休止角的计算式为:
\begin{array}{l} {\tan}\;\varphi =\\ \displaystyle\frac{{F_{\rm{A}}^{\rm{2}}\cot \;\phi \!\pm\! \!\!\sqrt {{{\left(\!\!F_{\rm{A}}^{\rm{2}}\cot\; \phi \!\!\right)}^2} \!\!-\!\! \left(\!\!F_{\rm{A}}^{\rm{2}} \!\!-\!\! F_{\rm{B}}^{\rm{2}}{{\cot }^2}\;\phi \!\!\right)\left(F_{\rm{A}}^{\rm{2}}{{\cot }^2}\;\phi \!\!-\!\! F_{\rm{B}}^{\rm{2}}{{\cot }^2}\;\phi \!\!\right)} }}{{F_{\rm{A}}^{\rm{2}} \!\!-\!\! F_{\rm{B}}^{\rm{2}}{{\cot }^2}\;\phi }} \end{array} (20) 2. 岩屑床休止角测量试验与经验系数修正
2.1 测量装置及材料
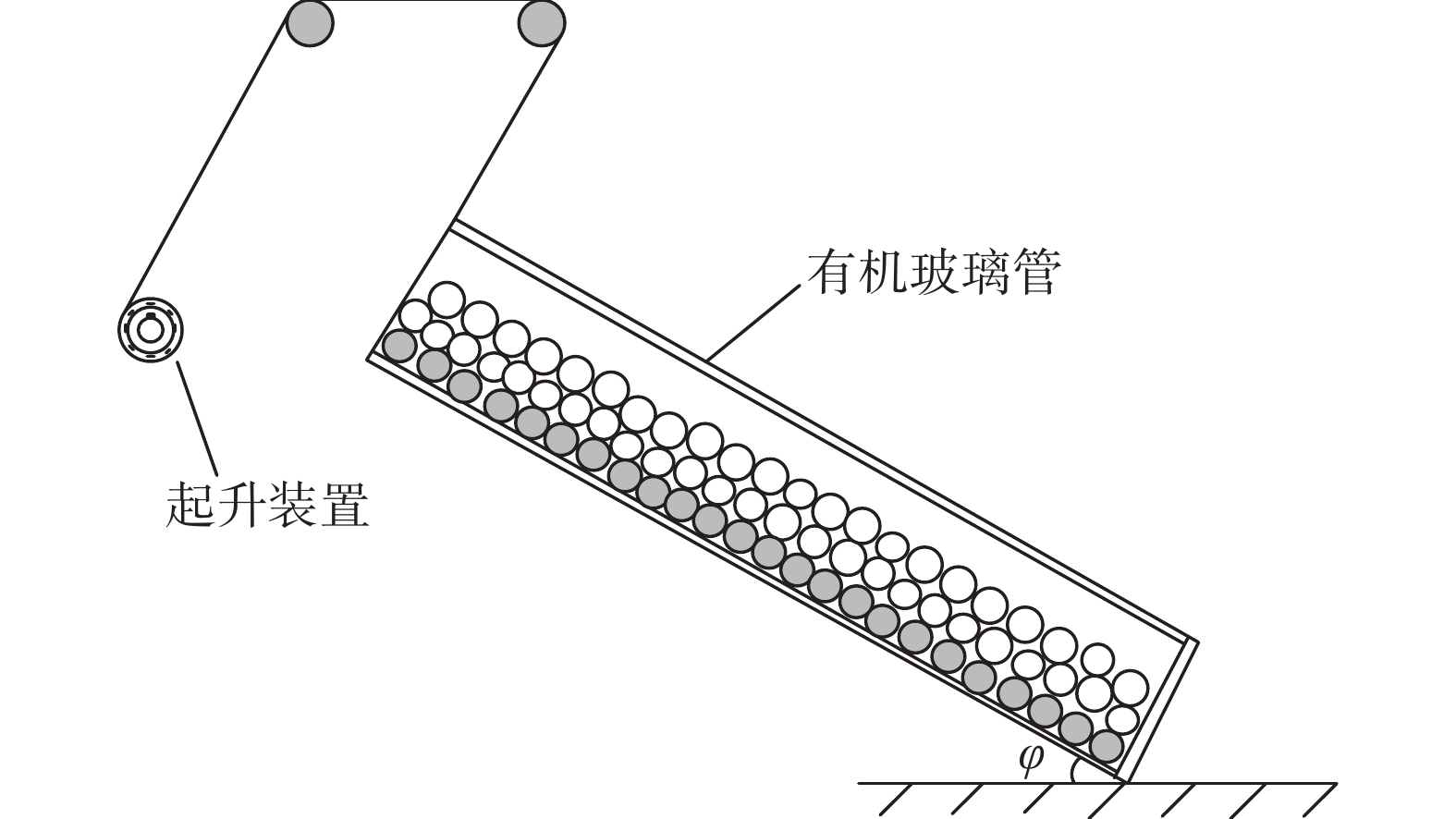
颗粒休止角的测量方法有很多种,主要有堆积法、挡板法、边坡法和倾斜法等。为了尽可能真实地模拟岩屑颗粒在大斜度井段的沉积与下滑,笔者采用倾斜法来测量岩屑床休止角。测量装置如图5所示:使用透明的有机玻璃管模拟井筒;用不同质量浓度的聚丙烯酰胺聚合物溶液(PAM)充当钻井液(即质量浓度为320,550,700和800 mg/L的PAM溶液);以筛分处理后的上返岩屑为研究对象进行试验,上返岩屑的密度为2 100~2 200 kg/m3,平均粒径为0.95 mm。
2.2 测量步骤与结果
利用标准筛对上返岩屑进行筛分处理;在有机玻璃管的低边固定岩屑,改变玻璃管内壁粗糙度;向玻璃管内注入PAM溶液,然后缓慢放入岩屑颗粒,平置有机玻璃管,并适度晃动使岩屑颗粒均匀分布于管壁低边,保证铺设的岩屑厚度至少大于10ds,封闭管口;将有机玻璃管置于试验台架上,启动提升装置,缓慢提升一端;仔细观察床面颗粒情况,当表面岩屑颗粒开始运动时,关闭启动装置,记录测斜仪角度,每组试验重复6次以减小测量误差;更换PAM溶液并重复上述步骤,直至试验完成。岩屑床休止角测量结果见表1。
表 1 岩屑床休止角测量结果Table 1. Results of the cuttings bed repose angle measurementPAM质量浓度/(mg·L–1) 休止角/(°) 休止井斜角/(°) PAM质量浓度/(mg·L–1) 休止角/(°) 休止井斜角/(°) 320 26.5 63.5 700 27.9 62.1 320 27.7 62.3 700 28.0 62.0 320 25.5 64.5 700 30.2 59.8 320 29.6 60.4 700 30.0 60.0 320 23.9 66.1 700 30.8 59.2 320 28.2 61.8 700 31.5 58.5 550 24.2 65.8 800 31.0 59.0 550 30.2 59.8 800 27.0 63.0 550 26.2 63.8 800 32.0 58.0 550 27.9 62.1 800 28.5 61.5 550 27.6 62.4 800 31.7 58.3 550 28.8 61.2 800 30.8 59.2 2.3 滑动休止角模型经验系数的修正
表1中,虽然随着PAM溶液质量浓度升高,个别测量值减小,但分析认为,这可能是试验误差所致,也可能是岩屑颗粒的排列差异性导致的,总体而言,随着PAM溶液浓度升高,岩屑床休止角呈增大趋势。PAM溶液质量浓度的变化,反映的是黏度的变化,即在实际钻井中,钻井液黏度越大,井底岩屑床休止角越大,表现在式(2)中就是相关系数的取值变化与颗粒表面液膜厚度不同。
利用试验结果计算摩擦系数,发现利用式(7)和式(10)计算出的结果存在一定误差。分析认为,这是由于当前岩屑休止角研究数据较少,本文所建楔入堆积模型中岩屑表面液膜厚度
\delta 参考了泥沙休止角的研究成果。为了尽可能减少这种误差,根据试验结果,对岩屑滑动休止角计算模型中的颗粒液膜厚度进行了修正:\begin{array}{l} {F_{\rm{e}}} = \dfrac{1}{2}{(1 + \dfrac{{\sqrt 2 }}{2})^2}({\gamma _{\rm{e}}} - \gamma ){\left[ {\eta ({d_{\rm{s}}} + 2\delta )} \right]^3}= \\ \;\qquad \dfrac{1}{2}{(1 + \dfrac{{\sqrt 2 }}{2})^2}({\gamma _{\rm{e}}} - \gamma ){ {({d_{\rm{s}}} + 2\lambda \delta )}^3} \end{array} (21) 变换式(21)得:
\lambda = \frac{{\eta \left( {{d_{\rm{s}}} + 2\delta } \right) - {d_{\rm{s}}}}}{{2\delta }} (22) 式中:
\lambda 和\eta 为液膜修正系数,其中\eta =0.998~1.048。根据所建岩屑床休止角预测模型中岩屑颗粒的液膜厚度参考值及岩屑粒径,利用式(22)计算出的液膜修正系数
\lambda 为0.974~1.618,以不同质量浓度PAM溶液中多次测量的平均值为准,得出不同质量浓度PAM溶液中岩屑颗粒液膜修正系数,并利用该修正系数计算颗粒表面液膜厚度,最后计算得出在320,550,700和800 mg/L PAM溶液中的岩屑床滑动休止角分别为24.2°、25.8°、27.1°和28.5°,而试验平均值分别为26.9°、27.5°、29.7°和30.2°。虽然理论值相较于试验值偏于保守,但从保证钻井作业安全的角度来说,更具有实际意义。3. 岩屑床休止角预测模型的计算
3.1 黏结力的影响
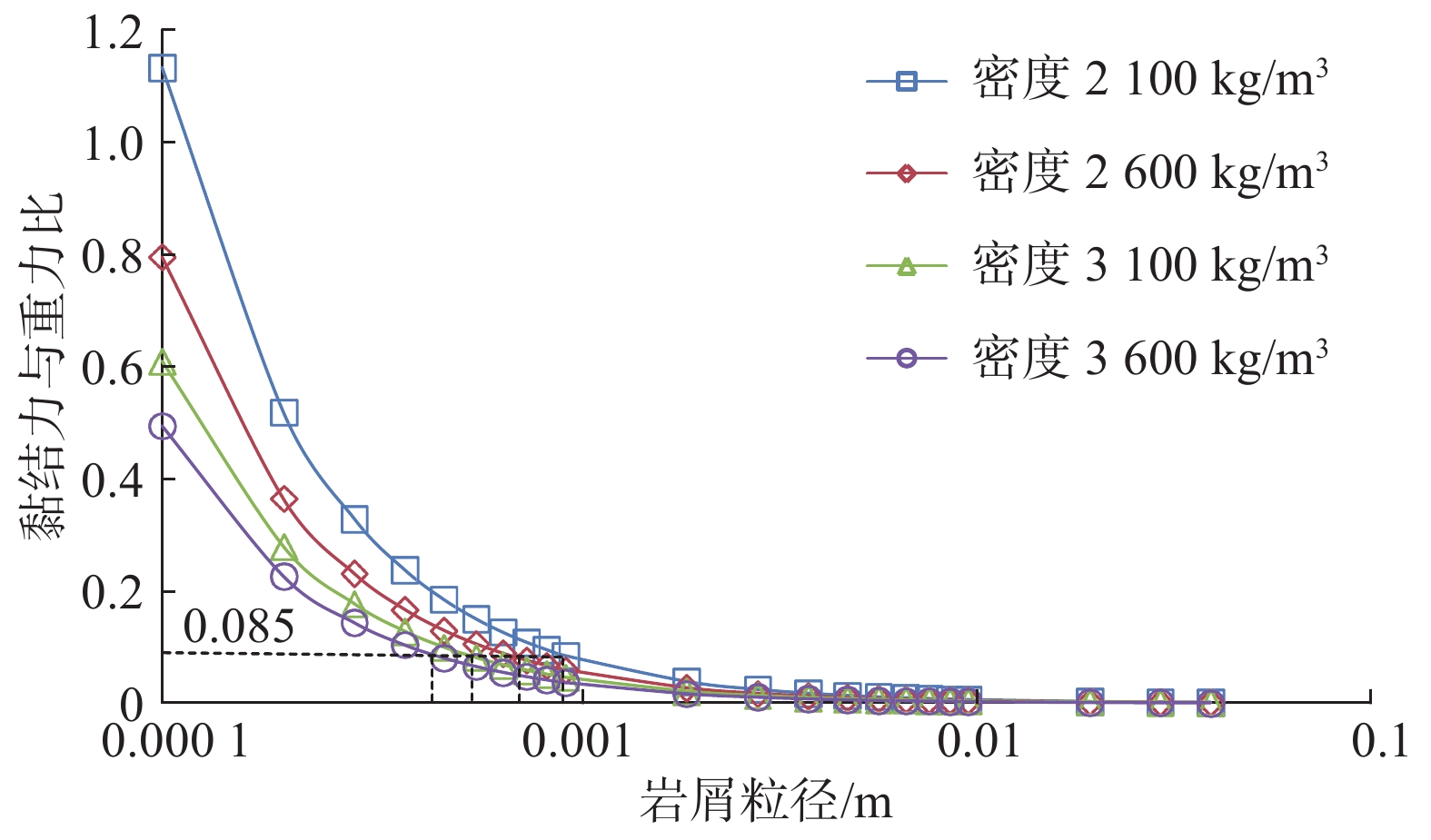
关于不同密度黏性颗粒休止角随粒径变化的规律在文献[18]中有详细论述:当黏性颗粒粒径大于1.0 mm时,黏结力对休止角的影响较小,这主要是由于黏结力与重力的比值减小,如图6所示。
从图6可以看出,黏结力与重力之比随岩屑粒径增大而减小。当粒径为1.0 mm时,最大黏结力与重力之比(岩屑密度为2 100 kg/m3)约为0.085;并且,在同一粒径下,岩屑的密度越大,其黏结力与重力之比越小,这表明对于密度较大的岩屑颗粒,计算其岩屑床休止角时可以忽略黏结力,即密度较大的岩屑颗粒在大斜度井段的沉积可以视为散体颗粒的堆积。
当黏结力趋近于0,即FB→0时,式(11)变为:
{\tan}\;\varphi = \frac{{{\eta ^3}{F_{\rm{e}}}}}{{{F_{\rm{A}}}}} - \frac{{\sqrt 2 }}{2} (23) 3.2 “+”和“–”的选择
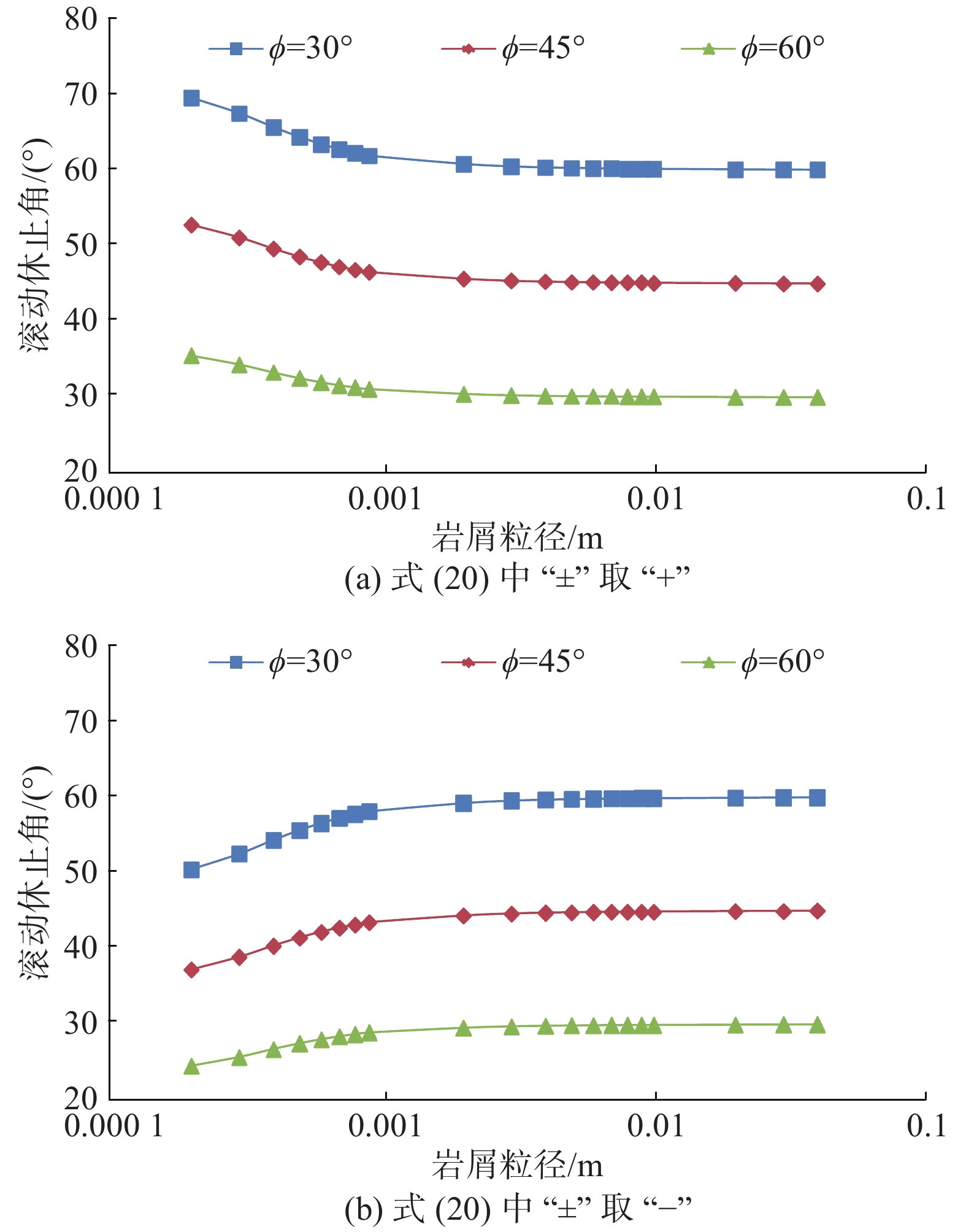
根据图4,当岩屑颗粒从平均岩屑床面滚动时,ϕ在
0 \sim \dfrac{{\text{π}} }{3} 变化,ϕ取不同值时,岩屑滚动休止角随粒径的变化曲线如图7所示。当式(20)中“±”取“+”时,计算结果如图7(a)所示;当取“–”时,计算结果如图7(b)所示。从图7可以看出,式(20)中“±”取“+”和“–”时,休止角随粒径的变化呈完全相反的趋势。但大量研究表明[11–15],除粉体颗粒(一般粒径<0.1 mm)和塑料沙的休止角随粒径增大而减小外,其余表面粗糙颗粒(一般粒径为0.1~40.0 mm)的休止角随粒径增大而增大。因此,从计算结果来看,式(20)中“±”取“–”时图7(b)的变化规律更符合实际。式(11)中“±”也取“–”,其原因类似。
由图7(b)可知:同一粒径下,ϕ越小,即岩屑颗粒排列越疏松,滚动休止角越大;相同排列情况下,滚动休止角随粒径增大而增大;但当粒径>1.0 mm时,变化趋于平缓;当
\phi = {60^ \circ } 时,颗粒排列最为紧密,滚动休止角最小,随着粒径增大,休止角逐渐接近于30°。由于实际钻井中岩屑粒径有大有小,排列呈现出“小中有大,大中有小”的特征,因此根据岩屑颗粒形态,当考虑岩屑床滚动休止角模型时,其休止角不超过30°这一取值更具有实际意义。4. 结论与建议
1)基于泥沙堆积楔入模型,分析了平均岩屑床面颗粒滚动与滑动时的受力情况,建立了大斜度井段岩屑床休止角预测模型,根据试验数据对预测模型用到的部分经验系数进行了修正。
2)室内测量试验发现,岩屑床休止角为23.9°~31.7°。受黏结力影响,岩屑床休止角随PAM溶液质量浓度与颗粒粒径增大而增大。通过计算和分析岩屑床滚动休止角,认为其稳定在25°~30°。
3)本文是以岩屑粒径相同为前提进行的研究,实际上返岩屑粒度分布变化多样,建议以后研究岩屑床休止角时,以粒度分析为基础,讨论不同级配对岩屑在钻井液中休止角的影响。
-
表 1 岩屑床休止角测量结果
Table 1 Results of the cuttings bed repose angle measurement
PAM质量浓度/(mg·L–1) 休止角/(°) 休止井斜角/(°) PAM质量浓度/(mg·L–1) 休止角/(°) 休止井斜角/(°) 320 26.5 63.5 700 27.9 62.1 320 27.7 62.3 700 28.0 62.0 320 25.5 64.5 700 30.2 59.8 320 29.6 60.4 700 30.0 60.0 320 23.9 66.1 700 30.8 59.2 320 28.2 61.8 700 31.5 58.5 550 24.2 65.8 800 31.0 59.0 550 30.2 59.8 800 27.0 63.0 550 26.2 63.8 800 32.0 58.0 550 27.9 62.1 800 28.5 61.5 550 27.6 62.4 800 31.7 58.3 550 28.8 61.2 800 30.8 59.2 -
[1] 孙开畅,刘林锋,明华军,等. 不同粒径及级配对碎石料休止角影响的实验研究[J]. 长江科学学院院报, 2016, 33(08): 91–95. SUN Kaichang, LIU Linfeng, MING Huajun, et al. Experimental research on the influence of particle size and gradation on repose angle of rockfill[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(08): 91–95.
[2] 王成华,张小刚,阙云,等. 粒状碎屑溜砂坡的形成和基本特征研究[J]. 岩土力学, 2007, 28(1): 29–35. WANG Chenghua, ZHANG Xiaogang, QUE Yun, et al. Formation and basic characteristics of sand-sliding slope composed of granular clasts[J]. Rock and Soil Mechanics, 2007, 28(1): 29–35.
[3] 王成华,阙云,李新坡,等. 粒状碎屑溜砂坡运动特征与动力数值分析[J]. 岩土力学, 2007, 28(2): 219–223. WANG Chenghua, QUE Yun, LI Xinpo, et al. Movement characteristics and dynamical numerical analysis of sand-sliding slope composed by granular[J]. Rock and Soil Mechanics, 2007, 28(2): 219–223.
[4] 吴国雄,曾榕彬,王成华,等. 溜砂坡的形成诱发因素及失稳破坏条件[J]. 中国铁道科学, 2006, 27(5): 7–12. WU Guoxiong, ZENG Rongbin, WANG Chenghua, et al. The inducing factors and the collapse conditions of sand-sliding slope[J]. China Railway Science, 2006, 27(5): 7–12.
[5] 孟震,杨文俊. 泥沙颗粒水下休止角与内摩擦角差异化初步探索[J]. 泥沙研究, 2012(4): 76–80. MENG Zhen, YANG Wenjun. Preliminary exploration of difference between submarine angle of repose and internal friction angle of sediment particles[J]. Journal of Sediment Research, 2012(4): 76–80.
[6] 孟震,杨文俊. 泥沙颗粒休止角与表层沙摩擦角研究进展[J]. 水力发电学报, 2015, 34(10): 117–129. MENG Zhen, YANG Wenjun. Angle of repose and angle of surface friction of sediment particles[J]. Journal of Hydroelectric Engi-neering, 2015, 34(10): 117–129.
[7] 孟震,王浩,杨文俊. 无黏性泥沙休止角与表层沙摩擦角试验[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(11): 1014–1022. MENG Zhen, WANG Hao, YANG Wenjun. Experiment on angle of repose and angle of surface friction of cohesionless sediment[J]. Journal of Tianjin University (Science and Technology), 2015, 48(11): 1014–1022.
[8] 熊绍隆. 深水孔口前冲刷漏斗形态研究[J]. 西北水电, 1983(4): 10–21. XIONG Shaolong. Study on shape of scouring funnel in front of deep water hole[J]. Northwest Hydropower, 1983(4): 10–21.
[9] 詹义正,谢葆玲. 散体泥沙的水下休止角[J]. 水电能源科学, 1996, 14(1): 56–59. ZHAN Yizheng, XIE Baoling. Under water angle of rest for non-cohesive sediment[J]. Water Resources and Power, 1996, 14(1): 56–59.
[10] 黄长伟,詹义正,卢金友. 黏性~散体均匀沙的动水休止角公式[J]. 广东水利水电, 2008(6): 1–3, 12. HUANG Changwei, ZHAN Yizheng, LU Jinyou. Movable water repose angle formula of uniform sand with viscosity[J]. Guangdong Water Resources and Hydropower, 2008(6): 1–3, 12.
[11] 张红武,汪家寅. 沙石及模型沙水下休止角试验研究[J]. 泥沙研究, 1989(3): 90–96. ZHANG Hongwu, WANG Jiayin. Experimental study on underwater angle of repose of sandstone and model sand[J]. Journal of Sediment Research, 1989(3): 90–96.
[12] 金腊华,石秀清. 试论模型沙的水下休止角[J]. 泥沙研究, 1990(3): 87–93. JIN Lahua, SHI Xiuqing. Discussion on underwater repose angle of model sand[J]. Journal of Sediment Research, 1990(3): 87–93.
[13] 王延贵,王兆印,曾庆华,等. 模型沙物理特性的试验研究及相似分析[J]. 泥沙研究, 1992(3): 74–83. WANG Yangui, WANG Zhaoyin, ZENG Qinghua, et al. Experi-mental study and similarity analysis of physical characteristics of model sand[J]. Journal of Sediment Research, 1992(3): 74–83.
[14] 漆海峰,郭晓镭,陆海峰,等. 煤粉的流动性测试及评价方法[J]. 化工学报, 2012, 63(2): 433–440. QI Haifeng, GUO Xiaolei, LU Haifeng, et al. Measurement of flow-ability of coal powders and research methods[J]. CIESC Journal, 2012, 63(2): 433–440.
[15] 王树传,高文元,屈有元. 含水量和粒度对粉粒状物料流动性的影响[J]. 大连轻工业学院学报, 1996, 15(2): 29–32. WANG Shuchuan, GAO Wenyuan, QU Youyuan. Influence of water content and grain on fluidity of powdery grained material[J]. Journal of Dalian Institute of Light Industry, 1996, 15(2): 29–32.
[16] 陈珊.变化水环境中散体沙休止角的初步研究[D].武汉: 武汉大学, 2014. CHEN Shan. Preliminary research on repose angle of granular sand in changing water environment[D]. Wuhan: Wuhan University, 2014.
[17] 唐存本. 泥沙起动规律[J]. 水利学报, 1963(2): 1–12. TANG Cunben. A law for incipient of sediment[J]. Journal of Hydraulic Engineering, 1963(2): 1–12.
[18] 詹义正, 黄卫东, 陈立, 等.均匀黏性–散体泥沙的统一水下休止角公式[C]// 黄河水利科学研究院.第六届全国泥沙基本理论研究学术讨论会论文集.郑州: 黄河水利出版社, 2005: 191-197. ZHAN Yizheng, HUANG Weidong, CHEN Li, et al. Unified underwater angle of repose formula for uniform viscosity-discrete sediment[C]//Yellow River Institute of Hydraulic Research. Proceedings of the 6th national seminar on sedimentary basic theoretical research. Zhengzhou: The Yellow River Water Conservancy Press, 2005: 191-197.
[19] 韩其为,王玉成,向熙珑. 淤积物的初期干容重[J]. 泥沙研究, 1981(1): 3–15. HAN Qiwei, WANG Yucheng, XIANG Xilong. Initial dry weight of sludge[J]. Journal of Sediment Research, 1981(1): 3–15.
[20] 武汉水利电力学院河流泥沙工程学教研室.河流泥沙工程学(上册)[M].北京: 水利电力出版社, 1980: 15. River Sediment Engineering Teaching and Research Section of Wuhan University of Hydraulic and Electric Engineering. River sediment engineering (Volume Ⅰ)[M]. Beijing: Water Resources and Electric Power Press, 1980: 15.




 下载:
下载: