S135钻杆接头缺口疲劳行为研究

李皓; 曾德智; 高定祥; 刘飞; 田刚; 施太和

doi:10.11911/syztjs.2019013

S135钻杆接头缺口疲劳行为研究

李皓^1,,
曾德智^1,*, ,,
高定祥²,
刘飞³,
田刚⁴,
施太和¹

1.
油气藏地质及开发工程国家重点实验室（西南石油大学），四川成都 610500
2.
中国石化西北油田分公司石油工程技术研究院，新疆乌鲁木齐 830011
3.
中国石化石油工程技术研究院，北京 100101
4.
中国石油新疆油田分公司工程技术研究院，新疆克拉玛依 834000

基金项目: 国家自然科学基金项目“静载、振动与腐蚀耦合作用下H₂S/CO₂气井完井管柱螺纹密封面的力化学损伤机制研究”（编号：51774249）、中国石化科技重大专项“顺北一区采输关键技术研究与应用”子课题“顺北一区高效采油技术研究”（编号：ZDP17004）联合资助

详细信息

作者简介:
李皓（1988—），男，甘肃陇南人，2011年毕业于兰州城市学院石油工程专业，2018年获西南石油大学油气井工程专业硕士学位，主要从事油气设施腐蚀与防护工作。E-mail：lihao1477024473@163.com

通讯作者:
曾德智，zengdezhi1980@163.com

中图分类号: TE28
计量
- 文章访问数: 12082
- HTML全文浏览量: 6378
- PDF下载量: 109
出版历程
- 收稿日期: 2018-05-29
- 修回日期: 2018-12-12
- 网络出版日期: 2019-01-16
- 刊出日期: 2019-06-30

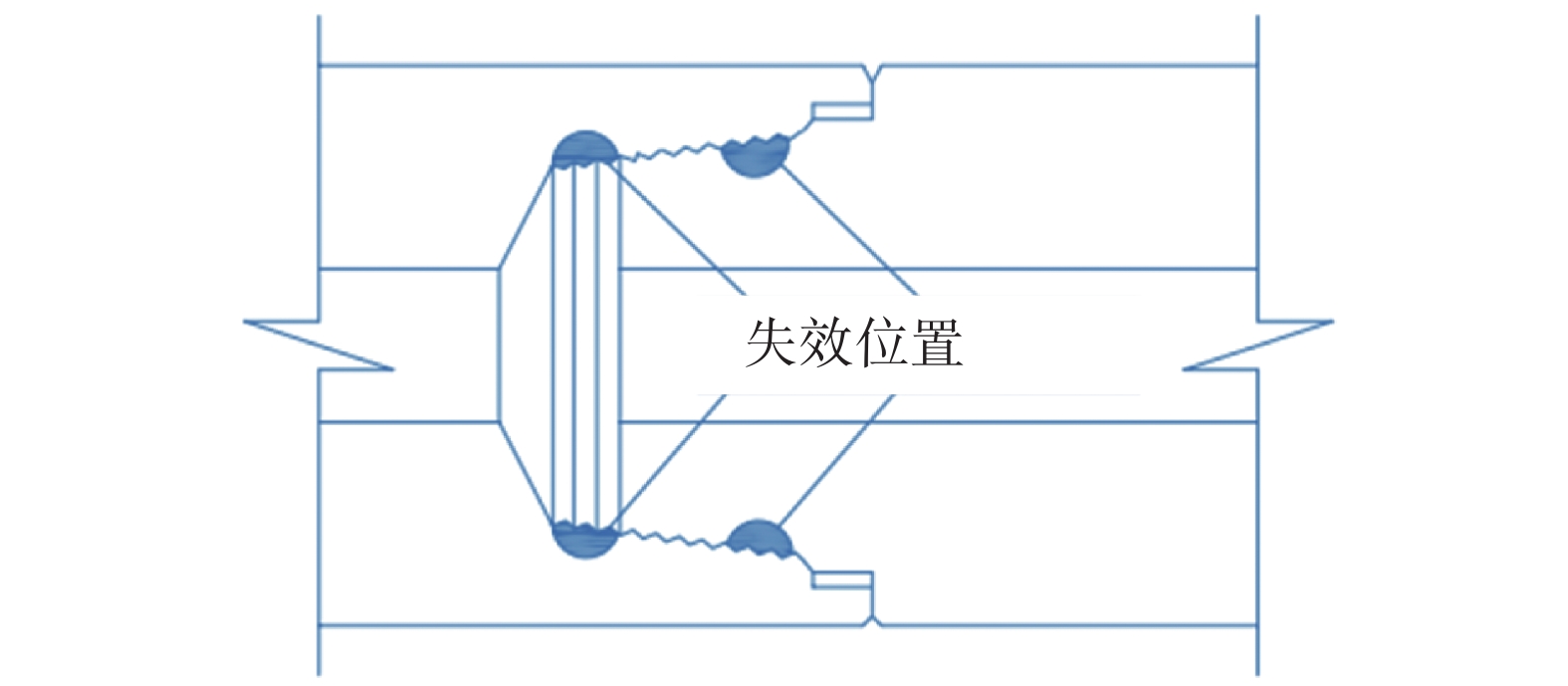
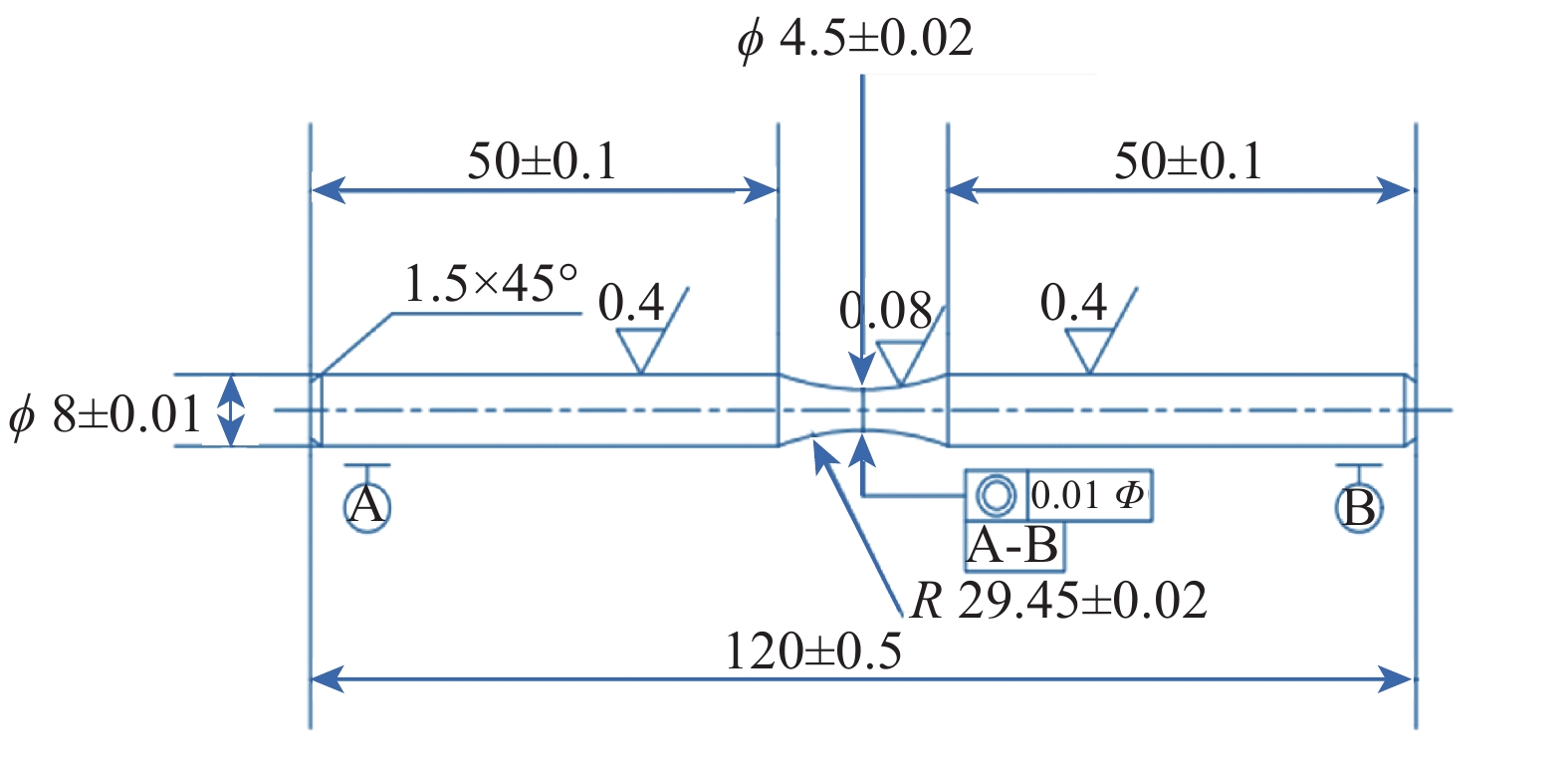
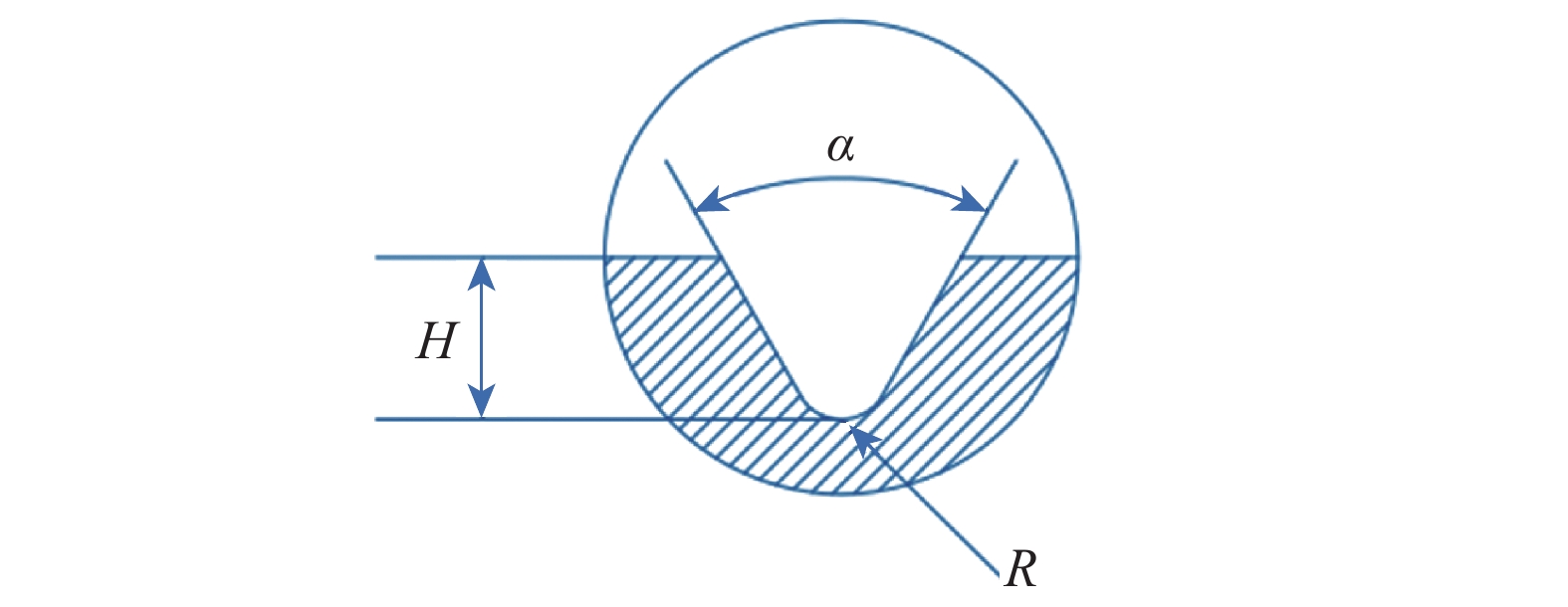
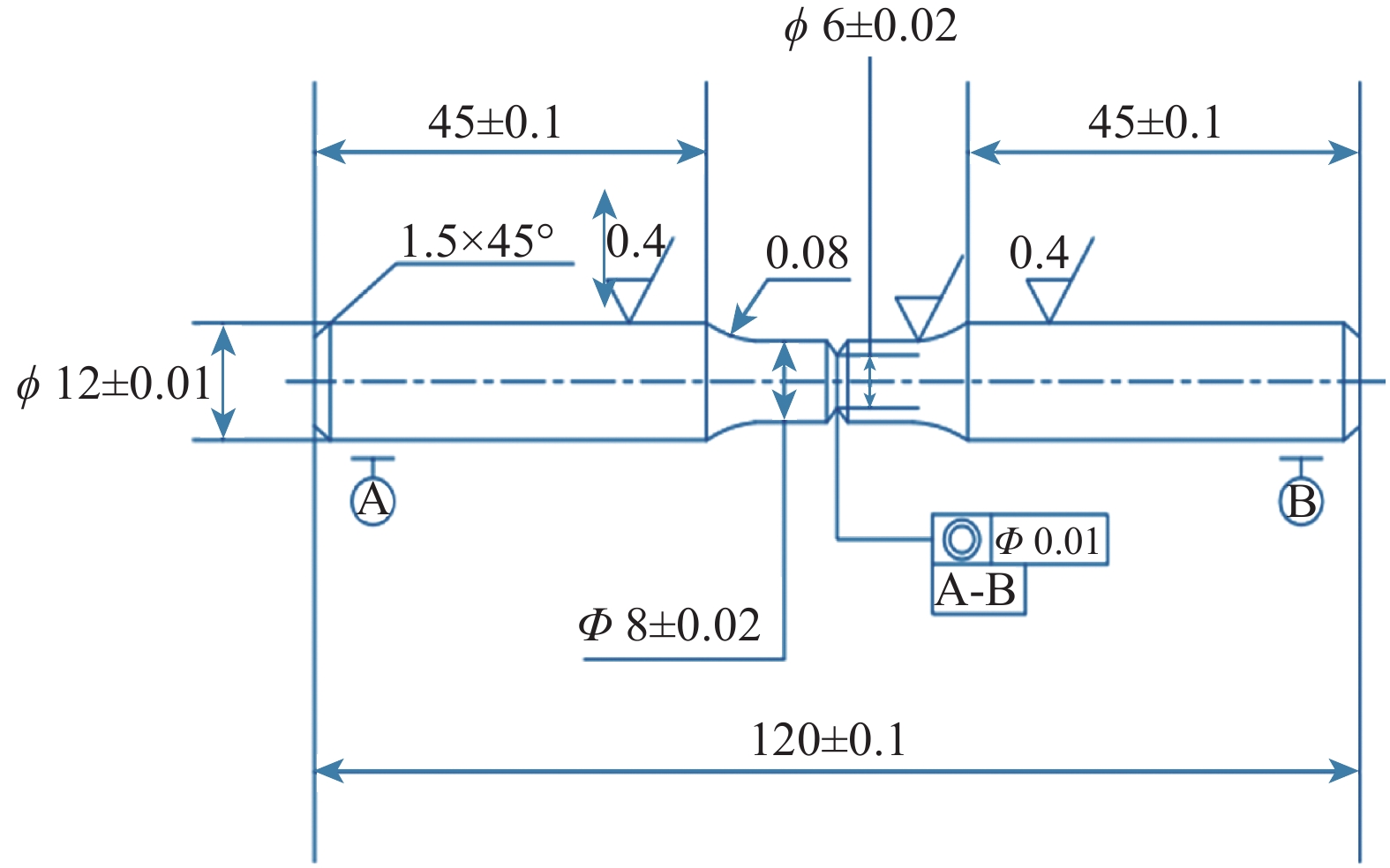
A Study of the Notch Fatigue Behavior of S135 Drill Pipe Joint

1.
State Key Laboratory of Oil & Gas Reservoir Geology and Exploration(Southwest Petroleum University), Chengdu, Sichuang, 610500, China
2.
Research Institute of Petroleum Engineering, Sinopec Northwest Oil Field Company, Urumqi, Xinjiang, 830011
3.
Sinopec Research Institute of Petroleum Engineering, Beijing, 100101, China
4.
Research Institute of Engineering Technology, PetroChina Xinjiang Oilfield Company, Karamay, Xijiang, 834000, China

摘要

摘要:
钻杆接头疲劳失效是钻杆失效的主要形式，因此，为提高钻杆的使用寿命，对S135钻杆接头的疲劳行为进行了研究。根据钻杆接头的受力特征设计了疲劳试样，采用PQ–6型旋转弯曲疲劳试验机和扫描电镜研究了应力集中对S135钻杆疲劳性能的影响。结果表明：S135钻杆疲劳性能对V形缺口具有一定的敏感性；缺口根部半径越小，应力集中系数越大，对疲劳性能的影响越严重，应力集中系数和疲劳强度符合幂函数关系；疲劳裂纹从缺口根部开始萌生，存在许多裂纹源（呈环形排列）；应力相同时，随着应力集中系数增大，缺口根部的撕裂现象减弱，断口变得光滑、平整，疲劳条纹变得细而密。研究结果表明：对钻杆接头螺纹的牙型进行优化设计，可以降低或减缓齿根的应力集中，降低S135钻杆疲劳对缺口的敏感性，提高S135钻杆的使用寿命。
- S135钻杆 /
- 钻杆接头 /
- 缺口疲劳 /
- 应力集中 /
- 断口形貌
Abstract:
Drill pipe joint fatigue is the main form of drill pipe failure. In order to improve the safety fatigue life of drill pipe, the notch fatigue behavior of S135 drill pipe joint has been studied. The fatigue specimens were designed according to the force characteristics of drill pipe joint, and the influence of stress concentration on the fatigue performance of S135 drill pipe was studied by PQ-6 rotary bending fatigue tester and scanning electron microscope. The results showed that the fatigue of S135 drill pipe exhibited certain sensitivity to the V-notch. The smaller the notch root radius, the larger the stress concentration factor, and the more serious impact on the fatigue performance. The stress concentration factor and the fatigue strength are in accordance with the power function relationship. The process is as follows: the fatigue crack starts from the root of notch, and many sources of cracks existed (in annular arrangement). When the stress is the same, the tearing phenomenon at the root of notch weakens with the increase of stress concentration factor, the fracture becomes smooth and flat, and the fatigue fringes become fine and dense. The research results showed that the optimal design of the drill pipe thread joint could reduce or alleviate the stress concentration of the root, reduce the fatigue sensitivity of S135 drill pipe to the notch, and improve the safety by better mapping the fatigue life of S135 drill pipe.
- S135 drill pipe /
- drill pipe joint /
- notch fatigue /
- stress concentration /
- fracture morphology

HTML全文

我国页岩气资源潜力巨大，实现页岩气经济效益开采对实现我国“双碳”发展目标具有重大意义。页岩地层钻完井过程中，当页岩与水基工作液（钻井液和压裂液）接触时，页岩自吸作用将驱动外部流体侵入页岩内部，诱发水化损伤，改变岩石结构，进一步促进自吸，导致页岩内部含水率上升、水化损伤加剧，显著影响页岩地层安全钻井与水力压裂效果^[1-9]。由此可见，自吸是影响页岩地层钻完井工程优化设计的重要参考指标。

针对页岩自吸作用，基于多孔介质渗吸理论，E. W. Washburn等人^[10-12]以Lucas-Washburn、Terzaghi和Handy自吸模型为基础，探索了页岩自吸趋势。在此基础上，研究人员考虑页岩自吸的特殊性，开展了针对性研究。Wu Zhongwei等人^[13-14]借助分形理论，明确了页岩孔隙的分形特征，建立了页岩分形自吸解析模型。何颂根等人^[15-16]考虑不同孔隙类型，将页岩孔隙分为有机质孔、黏土孔、脆性矿物孔，建立了多重孔隙自吸模型。K. Makhanov和Liang Lixi等人^[17-18]采用不同层理角度页岩，在室内进行了自吸试验，发现当自吸方向平行于页岩层理时，自吸量增加，说明层理属于高渗面，有利于自吸。针对页岩纳米孔隙发育特征，Wu Keliu等人^[19]指出纳米尺度下页岩自吸可能具备边界滑移现象，并给出了相应的自吸修正方程。Wang Xiukun和李江涛等人^[20-21]采用玻尔兹曼法、孔隙网络模拟等数值模拟手段，分析了流体在页岩纳米孔隙中的流动规律。

虽然目前已经对页岩自吸开展了大量研究，但主要针对页岩复杂孔隙结构特征，尤其以固定孔隙结构为前提。然而，页岩黏土矿物发育，自吸过程中同步发生水化反应，形成结构损伤，提供了新的自吸路径，导致页岩自吸具备典型的“动态”特征。目前，曾凡辉等人^[22-23]将自吸与核磁共振结合，证明了结构损伤对页岩自吸的促进作用。然而，如何实现水化损伤下的页岩自吸定量表征，是尚未解决的关键问题。因此，笔者聚焦水化损伤下的页岩动态自吸特征，通过室内试验，实现了自吸过程中页岩结构损伤的定量表征，建立了动态自吸毛细管力与动态迂曲度的计算方程，构建了页岩动态自吸模型，揭示了水化损伤对页岩自吸的影响机制，有助于科学、准确地评价页岩自吸特征与能力，为页岩地层钻完井优化设计提供理论支撑，助力我国页岩气的高效勘探开发。

1. 页岩自吸中的水化结构损伤特征

1.1 水化结构损伤

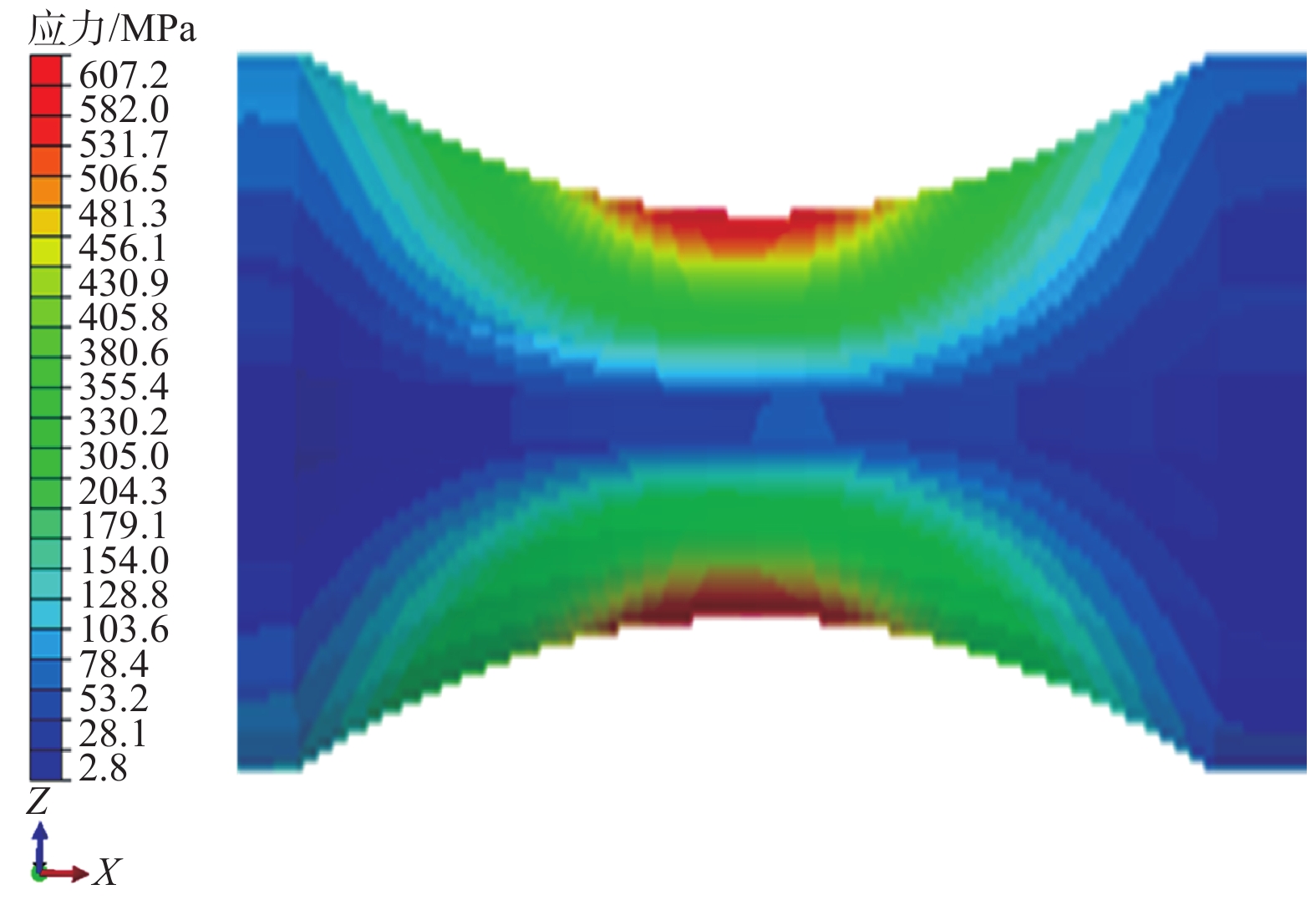
用四川盆地龙马溪组页岩岩样进行岩心自吸试验（悬吊岩样，下端面接触水），观测不同自吸时间下的页岩岩样表面，并测试页岩岩样不同自吸时间下的吸水量，结果如图1所示。由图1可知：随着自吸进行，水化结构损伤加剧，在24 h左右时岩样表面出现明显裂纹，而在自吸后期，裂纹没有进一步扩展趋势，表明前24 h是水化裂缝的主要发育段；在水化裂纹主要增长时间内（24 h内），页岩岩样吸水量的增幅最为显著。由此说明，水化裂纹是影响页岩吸水的主要因素。在此基础上，统计目前针对龙马溪组页岩的水化微观试验^[24-26]，以CT扫描、偏光显微镜等手段，观测页岩内部水化微裂纹的演化过程（见图2），发现页岩吸入水后水化导致微裂缝扩展演化，且水沿裂纹运移，最终在页岩表面形成宏观裂缝，从而显著提升页岩自吸能力。

图 1 页岩岩样自吸过程中表面及其吸水率的变化

Figure 1. Changes in surface and water absorption of shale rock samples during spontaneous imbibition

下载: 全尺寸图片幻灯片

图 2 页岩水化裂纹多尺度演化过程^[16-18]

Figure 2. Multiscale evolution process of shale hydration cracks^[16-18]

下载: 全尺寸图片幻灯片

1.2 结构损伤定量表征

通过测定页岩岩样不同自吸时间下的孔隙结构参数，可以建立水化结构损伤的定量表征方法。由于页岩孔隙具有多尺度特征，依靠单一测试方法难以准确获取页岩结构特征。因此，以自吸试验为基础，结合压汞与氮气吸附试验，实现自吸过程中页岩孔隙结构的定量表征^[27]。

以岩石基础物性（声波、电阻率及密度）为指标，选取相近2块岩样为一组，自吸不同时间并低温烘干后，一块岩样采用压汞法分析其孔径分布，一块岩样采用氮气吸附法分析其孔径分布，综合2类尺度下的孔径分布（见图3），确定不同自吸时间下的页岩平均孔径和孔隙度，结果如图4所示。由图4可知：随着自吸时间增长，水化造成的结构损伤增强，孔隙空间明显增大，平均孔径呈现增大趋势，在前24 h内孔隙结构参数变化最为剧烈；自吸后期，随着水化作用逐渐弱化，孔隙结构参数趋于稳定，整体变化趋势接近幂函数形式。原状页岩岩样平均孔径与孔隙度分别为7.5 nm和3.3%；受自吸过程中水化损伤的影响，当自吸达到稳定时，平均孔径与孔隙度增大至25.2 nm和6.3%。

图 3 氮气吸附、压汞及联合表征示意

Figure 3. Joint characterization of mercury intrusion and nitrogen adsorption

下载: 全尺寸图片幻灯片

图 4 页岩岩样自吸过程中平均孔径与孔隙度的变化

Figure 4. Changes in average pore size and porosity of shale rock samples during spontaneous imbibition

下载: 全尺寸图片幻灯片

2. 页岩自吸动态毛细管力与迂曲度分析

2.1 动态毛细管力分析

目前，研究页岩自吸时均将毛细管力设为定值，这在致密砂岩、碳酸盐岩等岩石自吸研究中具有适用性，但页岩地层强水化损伤会导致页岩孔隙结构发生变化。自吸过程中，页岩平均孔径的变化如图5所示。

图 5 页岩岩样自吸过程中的孔径变化示意

Figure 5. Evolution of pore size during spontaneous imbibition of shale rock samples

下载: 全尺寸图片幻灯片

由图5可知：无水化损伤时，自吸过程中页岩的平均孔径不发生变化；当产生水化损伤时，由于水化次生裂纹的演化，平均孔径在不断变化。

$\Delta \lambda (t)={\lambda }_{\text{a}}(t+\Delta t)-{\lambda }_{\text{o}}$

(1)

式中：∆λ(t)为自吸时刻t至t+∆t的平均孔径增量，nm； ${\lambda _{\text{o}}}$ 为原状平均孔径，nm； ${\lambda _{\text{a}}}(t + \Delta t)$ 为自吸时刻t+∆t的平均孔径，nm。

自吸过程中页岩发生水化损伤演变，页岩的平均孔径处于动态变化中，导致页岩毛细管力也在动态变化。为此，笔者通过自吸过程中的极限条件与平均孔径曲线的几何关系进行水化损伤表征，如图6所示。由图6可知，在任意自吸时刻，平均孔径曲线有2大极限条件，分别为坐标轴垂直方向与平行方向，其物理解释为：

图 6 页岩岩样自吸过程中的平均孔径演变示意

Figure 6. Evolution of average pore size during spontaneous imbibition of shale rock samples

下载: 全尺寸图片幻灯片

1）垂直方向上，孔径增长率dλ(t)/dt=∞，表明在自吸前缘水相介质遇见页岩基质，水化损伤作用瞬态完成，裂纹演化瞬间完成，此时平均孔径为自吸稳定下的最终页岩平均孔径λ_a^m，孔径增量∆λ=λ_a^m−λ_o；

2）平行方向上，孔径增长率dλ(t)/dt=0，表明在自吸前缘水相介质遇见页岩基质，没有水化损伤产生，平均孔径无增长，此时页岩平均孔径保持初始孔径λ_o，平均孔径增量∆λ=0。

基于此，可以得到任意自吸时刻t时水化作用对平均孔径影响的极限条件：

$\left\{ \begin{gathered} \Delta \lambda = \lambda _{\text{a}}^{\text{m}} - {\lambda _{\text{o}}}\;,\;\;\;\;\frac{{{\text{d}}{\lambda _{\text{a}}}(t)}}{{{\text{d}}t}} = \infty \\ \Delta \lambda = 0\;,\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\text{d}}{\lambda _{\text{a}}}(t)}}{{{\text{d}}t}} = 0 \\ \end{gathered} \right.$

(2)

确定2个极限条件以后，平均孔径曲线任意位置A（自吸任意时刻）的孔径增长速率位于2个极限条件之间 $\left(0 < \dfrac{{{\text{d}}{\lambda_{\text{a}}}(t)}}{{{\text{d}}t}}<\infty \right)$ 。基于平均孔径曲线上任意时间点位置处斜率与2个极限状态的几何关系，定义平均孔径变化系数 ${\delta _\lambda }(t)$ ：

${\delta _\lambda }(t) = (\lambda _{\text{a}}^{\text{m}} - {\lambda _{\text{o}}})\frac{{\arctan \dfrac{{{\text{d}}\lambda_{\text{a}} (t)}}{{{\text{d}}t}}}}{{\dfrac{{\text{π }}}{2}}}$

(3)

平均孔径变化系数的物理含义是某一自吸时刻下，水化损伤对平均孔径的影响程度。

将平均孔径变化系数代入毛细管力公式，可得动态毛细管力表达式：

${p_{\text{c}}}(t) = \frac{{4{\sigma _{\text{w}}}\cos \theta }}{{{\lambda _{\text{o}}} + (\lambda _{\text{a}}^{\text{m}} - {\lambda _{\text{o}}})\dfrac{{\arctan \dfrac{{{\text{d}}\lambda_{\text{a}} (t)}}{{{\text{d}}t}}}}{{\dfrac{{\text{π }}}{2}}}}}$

(4)

式中： ${p_{\text{c}}}(t)$ 为动态毛细管力，MPa； ${\sigma _{\text{w}}}$ 为表面张力，N/m； $\theta$ 为润湿角，（°）。

2.2 动态迂曲度分析

流体进入岩石内的多孔介质后，在其内部流动时，由于多孔介质颗粒的分布、形态等具有非均质性，流体的流线是弯曲的，对于流线的弯曲特征，通常采用迂曲度（τ）来描述。由于技术所限，目前难以将一块岩样所有位置的迂曲度全部提取出来，因此，采用平均迂曲度进行分析。

${\tau_{\text{a}}} = \frac{1}{n}\sum\limits_i {{\tau _i}} \;\;\quad (i = 1,2,3,\cdots ,n)$

(5)

式中： ${\tau _{\text{a}}}$ 为平均迂曲度；τ_i为第i条流线迂曲度；n为流线数量。

假定页岩颗粒为球形颗粒与方体颗粒，分别获取球形颗粒与方体颗粒下的典型流线（分别为直线形、Z字形和曲面形）^[28-29]，如图7所示。页岩平均迂曲度的表达式为：

图 7 圆球与方体颗粒下的各类流动类型

Figure 7. Various flow types under circular and square particles

下载: 全尺寸图片幻灯片

${\tau _{\text{a}}} = \left(1 - \phi \right)\left\{ {\dfrac{{1 + \sqrt 3 \dfrac{\dfrac{2}{3}\sqrt {\dfrac{{\sqrt 3 {\text{π }}}}{{1 - \phi }}} }{2}}}{{\sqrt 3 \dfrac{\dfrac{2}{3}\sqrt {\dfrac{{\sqrt 3 {\text{π }}}}{{1 - \phi }}} }{2}}} + \dfrac{{\sqrt 3 \dfrac{\dfrac{2}{3}\sqrt {\dfrac{{\sqrt 3 {\text{π }}}}{{1 - \phi }}} }{2}{\text{ + }}\dfrac{{{\text{π}} - 2}}{2}}}{{\sqrt 3 \dfrac{\dfrac{2}{3}\sqrt {\dfrac{{\sqrt 3 {\text{π }}}}{{1 - \phi }}} }{2}}}} \right. + \;1{\text{ + }}\dfrac{1}{2}\sqrt {1 - \phi } {\text{ + }}\left. {\dfrac{{\sqrt {{{\left(\dfrac{1}{{\sqrt {1 - \phi } }} - 1\right)}^2} + {{\dfrac{1}{4}}}} }}{{\dfrac{1}{{\sqrt {1 - \phi } }} - 1}}} \right\}{\text{ + }}\phi$

(6)

式中： $\phi$ 为孔隙度。

依据水化损伤下的孔隙度变化趋势，基于3.1节的方法，建立不同自吸时间下孔隙度变化幅度表达式：

${\delta _\phi }(t) = (\phi _{\text{a}}^{\text{m}} - {\phi _{\text{o}}})\frac{{\arctan \dfrac{{{\text{d}}{\phi _{\text{a}}}(t)}}{{{\text{d}}t}}}}{{\dfrac{{\text{π }}}{2}}}$

(7)

式中： ${\delta _\phi }(t)$ 为自吸t时刻下孔隙度的变化幅度； $\phi _{\text{a}}^{\text{m}}$ 为自吸稳定后的孔隙度； ${\phi _{\text{o}}}$ 为原状孔隙度。

结合式（6）和式（7），可获得水化损伤下页岩动态迂曲度的表达式：

$\begin{gathered} {\tau _{\text{a}}}\left(t\right) = \left\{ {1 - [\phi {\text{ + }}{\delta _\phi }\left(t\right)]} \right\}\left\{ {\dfrac{{1 + \sqrt 3 \dfrac{\dfrac{2}{3}\sqrt {\dfrac{{\sqrt 3 {\text{π }}}}{{1 - [\phi {\text{ + }}{\delta _\phi }\left(t\right)]}}} }{2}}}{{\sqrt 3 \dfrac{\dfrac{2}{3}\sqrt {\dfrac{{\sqrt 3 {\text{π }}}}{{1 - [\phi {\text{ + }}{\delta _\phi }\left(t\right)]}}} }{2}}} + \dfrac{{\sqrt 3 \dfrac{\dfrac{2}{3}\sqrt {\dfrac{{\sqrt 3 {\text{π }}}}{{1 - [\phi {\text{ + }}{\delta _\phi }\left(t\right)]}}} }{2}{\text{ + }}\dfrac{{{\text{π }} - 2}}{2}}}{{\sqrt 3 \dfrac{\dfrac{2}{3}\sqrt {\dfrac{{\sqrt 3 {\text{π }}}}{{1 - [\phi {\text{ + }}{\delta _\phi }\left(t\right)]}}} }{2}}}} \right. + \;1{\text{ + }} \\ \;\;\;\;\; \\ \qquad\qquad\qquad\dfrac{1}{2}\sqrt {1 - [\phi {\text{ + }}{\delta _\phi }\left(t\right)]} {\text{ + }}\left. {\dfrac{{\sqrt {{{\left(\dfrac{1}{{\sqrt {1 - [\phi {\text{ + }}{\delta _\phi }\left(t\right)]} }} - 1\right)}^2} + \dfrac{1}{4}} }}{{\dfrac{1}{{\sqrt {1 - [\phi {\text{ + }}{\delta _\phi }\left(t\right)]} }} - 1}}} \right\}{\text{ + }}[\phi {\text{ + }}{\delta _\phi }\left(t\right)]\;\;\;\;\; \\ \end{gathered}$

(8)

3. 页岩动态自吸物理模型

3.1 自吸模型构建

对于页岩自吸，毛细管力为主控驱动力。此外，由于黏土–水分子的双电层效应，页岩具有半透膜特征^[30]，因此，渗透压也是驱动力，其计算公式为：

${p_{\text{π }}} = \eta \frac{{RT}}{{\bar V}}\ln \frac{{{a_{\text{n}}}}}{{{a_{\text{m}}}}}$

(9)

式中： ${p_{\text{π }}}$ 为渗透压，Pa； $\bar V$ 为水的偏摩尔体积，m³/mol； ${a_{\text{m}}}$ 为岩石活度； ${a_{\text{n}}}$ 为外部流体活度； $T$ 为温度，K；R为气体常数，J/（mol·K）； $\eta$ 为膜效率。

同时，由于本文探讨的自吸模式为垂直端面自吸，重力为阻力。因此，综合毛细管力、渗透压及重力，依据LW自吸模型，得到自吸表达式：

$\frac{{{\text{d}}{L_{\text{t}}}}}{{{\text{d}}t}} = \frac{{{\lambda ^2}}}{{32{\mu_{\text{w}}}{L_{\text{t}}}}}\left( {\frac{{4{\sigma _{\text{w}}}\cos \theta }}{\lambda } + \eta \frac{{RT}}{{\bar V}}\ln \frac{{{a_{\text{n}}}}}{{{a_{\text{m}}}}} - \rho g{L_{\text{s}}}} \right)$

(10)

式中： ${L_{\text{t}}}$ 为弯曲毛细管实际吸水长度，m； ${L_{\text{s}}}$ 为吸水直线长度，m； ${\mu_{\text{w}}}$ 为液体黏度，Pa·s； $\rho$ 为液体密度，kg/m³； $g$ 为重力加速度，m/s²。

根据迂曲度的定义得知 $\tau = \dfrac{{{L_{\text{t}}}}}{{{L_{\text{s}}}}}$ ， ${v_{\text{t}}} = \tau {v_{\text{s}}}$ ，从而式（10）可以写为：

$\frac{{{\text{d}}{L_{\text{s}}}}}{{{\text{d}}t}}{\text{ = }}\frac{{{\lambda ^2}}}{{32{\mu_{\text{w}}}{\tau ^2}}}\left( {\frac{{4{\sigma _{\text{w}}}\cos \theta }}{\lambda } + \eta \frac{{RT}}{{\bar V}}\ln \frac{{{a_{\text{n}}}}}{{{a_{\text{m}}}}}} \right)\frac{1}{{{L_{\text{s}}}}} - \frac{{{\lambda ^2}\rho g}}{{32{\mu_{\text{w}}}{\tau ^2}}}$

(11)

当自吸达到稳定时，水上升的速度 $\dfrac{{{\text{d}}{L_{\text{s}}}}}{{{\text{d}}t}} = 0$ ，可以求解得到平衡高度。基于自吸初始条件L_s=0，对式（11）积分，可得单根弯曲毛细管的吸水方程：

$\left\{ \begin{gathered} t = - \frac{{{A_{\text{h}}}}}{{B_{\text{h}}^2}}\ln \left(1 - \frac{{{B_{\text{h}}}}}{{{A_{\text{h}}}}}{L_{\text{s}}}\right) - \frac{{{L_{\text{s}}}}}{{{B_{\text{h}}}}} \\ {A_{\text{h}}} = \frac{{{\lambda ^2}\left( {\dfrac{{4{\sigma _{\text{w}}}\cos \theta }}{\lambda } + \eta \dfrac{{RT}}{{\bar V}}\ln \frac{{{a_{\text{n}}}}}{{{a_{\text{m}}}}}} \right)}}{{32{\mu_{\text{w}}}{\tau ^2}}}\;\; \\ {B_{\text{h}}} = \frac{{\rho g{\lambda ^2}}}{{32\mu_{\text{w}}{\tau ^2}}} \\ \end{gathered} \right.$

(12)

在此基础上，进一步考虑水化结构损伤，融入动态毛细管力与动态迂曲度，代入式（12），进而得到水化损伤下的页岩动态自吸方程：

$\frac{{{\text{d}}{L_{\text{s}}}}}{{{\text{d}}t}} = \frac{{{{[{\lambda _{\text{o}}} + {\delta _\lambda }(t)]}^2}}}{{32{\mu_w}{{\left\{ {{\tau _{\text{a}}}[{\phi _{\text{o}}} + {\delta _\phi }(t)]} \right\}}^2}{L_{\text{s}}}}}\left\{ {\frac{{4\sigma_{\text{w}} \cos \theta }}{{{\lambda _{\text{o}}} + {\delta _\lambda }(t)}}{\text{ + }}\eta \frac{{RT}}{{\bar V}}\ln \left(\frac{{{a_{\text{n}}}}}{{{a_{\text{m}}}}}\right)} \right\} - \frac{{\rho g{{[{\lambda _{\text{o}}} + {\delta _\lambda }(t)]}^2}}}{{32{\mu_{\text{w}}}{{\left\{ {{\tau _{\text{a}}}[{\phi _{\text{o}}} + {\delta _\phi }(t)]} \right\}}^2}}}$

(13)

采用数值积分方法，利用插值方法对式（13）积分。基于插值法原理，对被积函数f(x)进行n次插值，可逼近积分值。积分过程为：

$\left\{ \begin{gathered} \int_a^b {f(x){\text{d}}x \approx \sum\limits_{k = 0}^n {f({x_k})\int_a^b {{l_k}(x){\text{d}}x} } } \\ \int_a^b {{l_k}(x){\text{d}}x} = \int_a^b {{\prod _{j \ne k}}\frac{{x - {x_j}}}{{{x_k} - {x_j}}}{\text{d}}x} \\ \end{gathered} \right.$

(14)

利用上述吸水方程可求得平均孔径下的单个毛细管内吸水长度。页岩内部存在多根毛细管，借助多束毛细管模型（见图8），求取自吸体积（ ${V_i}(t)$ ）：

图 8 岩石多束毛管模型^[31]

Figure 8. Rock multi-bundle capillary model^[31]

下载: 全尺寸图片幻灯片

$\begin{split}& \\ &{V_i}(t) = {L_{\text{s}}}(t){A_{\text{p}}} = {L_{\text{s}}}A\phi (t) \end{split}$

(15)

式中：A_p为孔隙横截面，m²。

值得注意的是，对于某一时刻（如t时刻）的吸水量，需选择对应时刻的 $\phi (t)$ 。基于吸水体积和流体密度，可得到该时刻下的吸水质量，进而利用吸水质量与岩样初始质量的比值，求得岩样的吸水率：

$w(t) = \frac{{W(t) - {W_{\text{o}}}}}{{{W_{\text{o}}}}} = \frac{{\rho {V_i}(t)}}{{{W_{\text{o}}}}}$

(16)

页岩动态自吸模型求解流程如图9所示。由图9可知，本文所构建模型考虑了水化作用所形成渗透压、动态毛细管力及动态迂曲度的影响，更符合页岩自吸实际情况。

图 9 页岩动态自吸模型求解流程

Figure 9. Solution process for shale dynamic spontaneous imbibition model

下载: 全尺寸图片幻灯片

3.2 自吸模型验证

利用本文模型预测页岩岩样的自吸曲线，并与页岩岩样实际自吸曲线对比，以验证模型的准确性。图10为3个页岩岩样的实际自吸曲线与模型预测自吸曲线的对比。由图10可知，3个页岩岩样的自吸曲线与模型预测自吸曲线的对应性较好，部分区域有一定偏差，这主要是因为每个岩样的非均质性及页岩物性测试中可能存在偏差。验证结果表明，本文构建的动态自吸模型对页岩岩样具有很好的适用性，能够准确预测页岩自吸情况。

图 10 模型预测自吸曲线与实际自吸曲线的对比

Figure 10. Comparison between the model predicted and actual spontaneous imbibition curves

下载: 全尺寸图片幻灯片

3.3 模型对比分析

基于本文构建的自吸模型，以驱动力和迂曲度分类，开展了不同类型自吸模型对比分析，结果如图11所示。由图11可知：

图 11 不同自吸模型预测自吸曲线的对比

Figure 11. Comparison of predicting spontaneous imbibition curves by different spontaneous imbibition models

下载: 全尺寸图片幻灯片

1）当毛细管流线特性一定时（见图11（a）），忽略渗透压，驱动力较小时预测的自吸量偏小，由此可以看出，页岩的半透膜效应对自吸具有促进作用；忽略水化损伤导致的毛细管力变化，会导致预测过程中的驱动力较大（流动阻力保持定值），造成预测的自吸量偏大。

2）当驱动力一定时（见图11（b）），假设毛细管为平直毛细管，忽略弯曲毛细管的流动阻力时，预测的自吸量较大。考虑静态弯曲毛细管的流动阻力时，预测的自吸量明显偏小，这主要是因为，随着水化损伤增加，迂曲度降低，流动阻力降低，导致考虑静态弯曲毛细管时预测的自吸量偏低。

3）综合对比，本文构建的动态自吸模型的预测自吸曲线与实测自吸曲线拟合程度最好，说明了水化损伤对页岩自吸的重要性。此外，也说明水化损伤同步作用于自吸驱动与自吸阻力，必须同时考虑两者的动态变化，才能科学表征页岩的自吸。

4. 页岩自吸影响因素分析

基于本文构建的动态自吸模型，进行了页岩动态自吸影响因素分析，结果如图12所示。由图12可知：随着孔隙度增大，页岩内部储集流体的空间增大，吸水通道随之增大，使内部毛细管迂曲度减轻，造成流动阻力降低，从而使自吸能力显著提高。随着迂曲度增大，页岩内部毛细管道更为曲折，流动阻力更大，水更难吸入页岩内部，导致自吸量显著减小。

图 12 页岩动态自吸影响因素分析

Figure 12. Analysis of factors influencing shale dynamic spontaneous imbibition

下载: 全尺寸图片幻灯片

更为明显的是，随着迂曲度增大，自吸平衡时间明显增长。因为高迂曲度对应高流动阻力，使吸水流动过程放缓。因此，低迂曲度下，自吸效应能更快达到平衡。随着外部流体活度增大，水化作用增强，对页岩结构损伤更为严重，产生更多水化裂纹，使流动空间增大，从而利于外部流体侵入页岩，加剧自吸。同时，外部流体活度较大，易在页岩内外形成较大活度差。当膜效率一定时，高活度差将导致渗透压增大，增大了页岩外部驱动力。随着接触角减小，亲水性增加，毛细管力增强，导致自吸量增大，页岩自吸能力增强。

5. 结　论

1）随着自吸时间延长，水化损伤加剧，前24 h是水化裂缝的主要发育阶段，自吸后期水化损伤达到稳定。自吸过程中在水化损伤作用下，页岩平均孔径与孔隙度呈现明显增大趋势，当自吸达到稳定状态时，试验所用页岩岩样的平均孔径与孔隙度分别提升至约25.2 nm和6.3%。

2）考虑水化结构损伤的影响，建立了自吸过程中页岩动态毛细管力与动态迂曲度的表达式。在此基础上，融入LW自吸模型，构建了页岩动态自吸模型，并验证了模型的准确性与适用性。

3）通过对比分析自吸模型，论证了水化损伤对自吸驱动与自吸阻力的同步作用效应，因此必须考虑水化损伤下的动态驱动力与动态自吸阻力，才能精准表征页岩的自吸。

4）利用构建的页岩动态自吸模型，分析了影响页岩自吸的因素，发现随孔隙度增大、迂曲度降低、流体活度增大及接触角减小，页岩具备更强的驱动力与更小的流动阻力，自吸速率与自吸量均显著提升。

图 1 钻杆接头疲劳失效位置

Figure 1. Fatigue failure position of drill pipe joint

下载: 全尺寸图片幻灯片

图 2 光滑试样（单位：mm）

Figure 2. Smooth specimen (unit: mm)

下载: 全尺寸图片幻灯片

图 3 V形缺口几何特征和参数定义

Figure 3. The geometric feature and parameter definition of V-notch

下载: 全尺寸图片幻灯片

图 4 缺口试样（单位：mm）

Figure 4. Notch specimen (unit: mm)

下载: 全尺寸图片幻灯片

图 5 光滑试样的等效应力云图

Figure 5. Equivalent stress nephogram of a smooth specimen

下载: 全尺寸图片幻灯片

图 6 缺口试样的等效应力云图

Figure 6. Equivalent stress map of notched specimen

下载: 全尺寸图片幻灯片

图 7 不同应力集中系数K_t下应力升降示意图

Figure 7. Schematic diagram of stress fluctuation under different K_t

下载: 全尺寸图片幻灯片

图 8 应力集中系数与疲劳强度的关系

Figure 8. Relationship between stress concentration factor and fatigue strength

下载: 全尺寸图片幻灯片

图 9 不同应力集中程度下的S–N曲线

Figure 9. S–N cures at different stress concentration degrees

下载: 全尺寸图片幻灯片

图 10 光滑试样在空气中的疲劳断口

Figure 10. Fatigue fracture of a smooth specimen in air

下载: 全尺寸图片幻灯片

图 11 缺口试样在空气中的疲劳断口（K_t=2.23）

Figure 11. Fatigue fracture of notch specimen in air (K_t=2.23)

下载: 全尺寸图片幻灯片

图 12 缺口试样在空气中的疲劳断口（K_t=4.11）

Figure 12. Fatigue fracture of notch specimen in air (K_t=4.11)

下载: 全尺寸图片幻灯片

图 13 K_t=3.01缺口试样在空气中的疲劳断口

Figure 13. Fatigue fracture of notch sample in air(K_t=3.01)

下载: 全尺寸图片幻灯片

表 1 缺口应力集中对S135钻杆疲劳性能影响的试验方案

Table 1 Test Scheme for the Influence of Notch Stress Concentration on Fatigue Behavior of S135 Drill Pipe

组号	试样类型	H/mm	α/（°）	R/mm	K_t	环境
1	光滑				1.00	空气
2	缺口	1.0	90	0.1	4.11	空气（常温）
3				0.2	3.01
4				0.4	2.23
5				0.6	1.93
注：K_t为理论应力集中系数， ${K_{\rm{t}}} = {{{\sigma _{\max }}} / \sigma }$ ； ${\sigma _{\max }}$ 为缺口截面上的最大应力，MPa； $\sigma$ 为缺口截面上的平均应力，MPa^[13]。

下载: 导出CSV

表 2 缺口疲劳系数及缺口敏感性计算结果

Table 2 Calculation results of notch fatigue coefficient and notch sensitivity

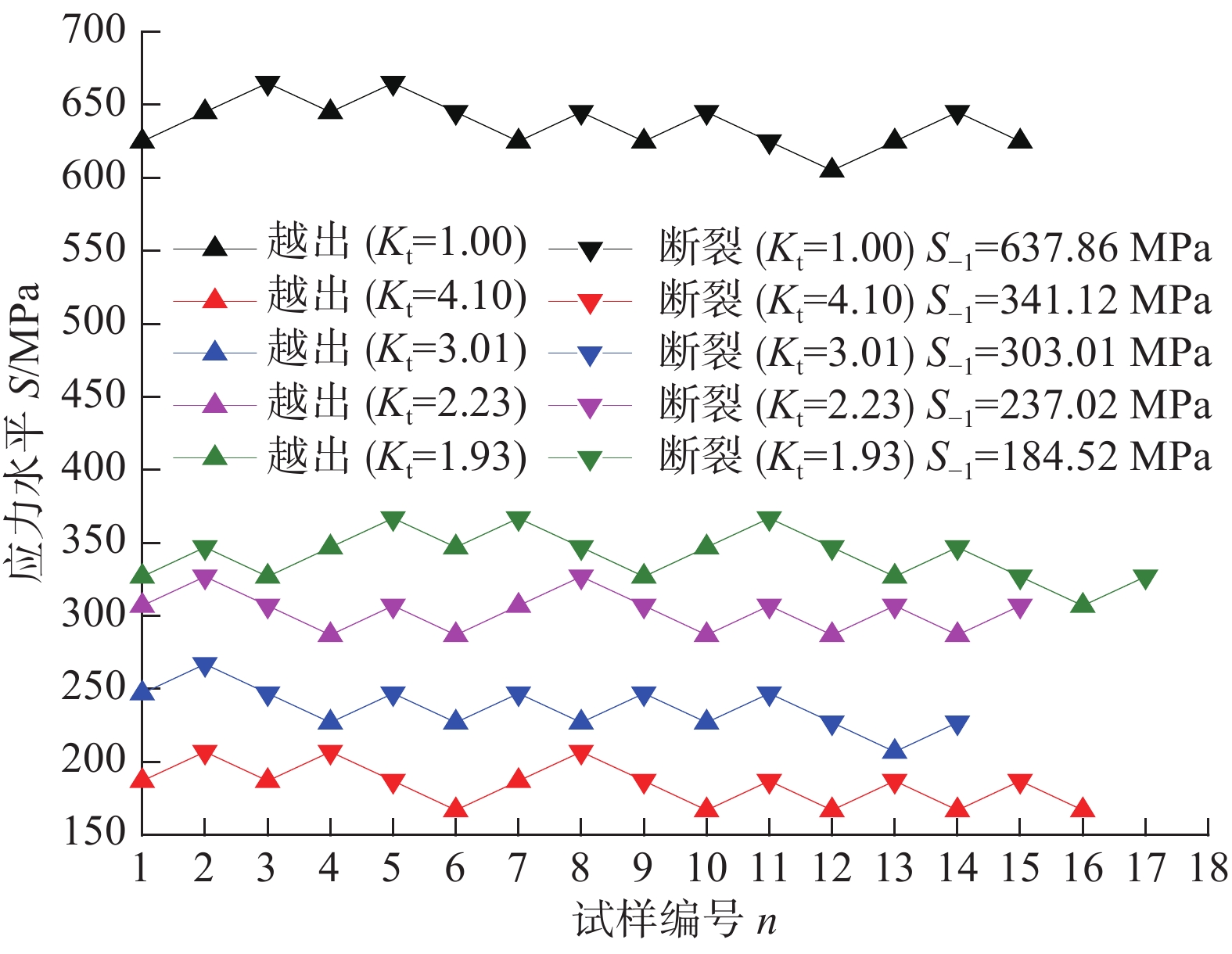
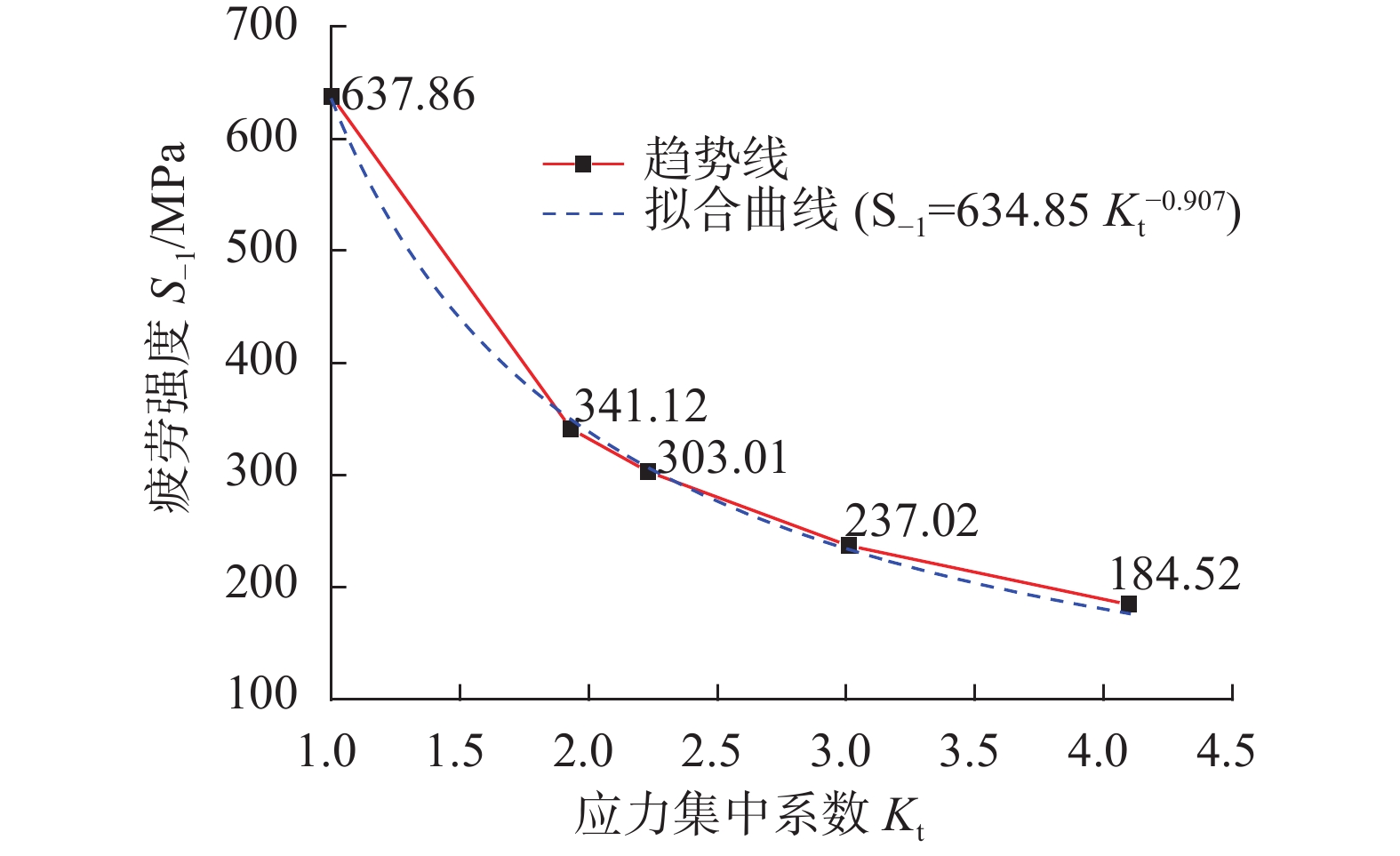
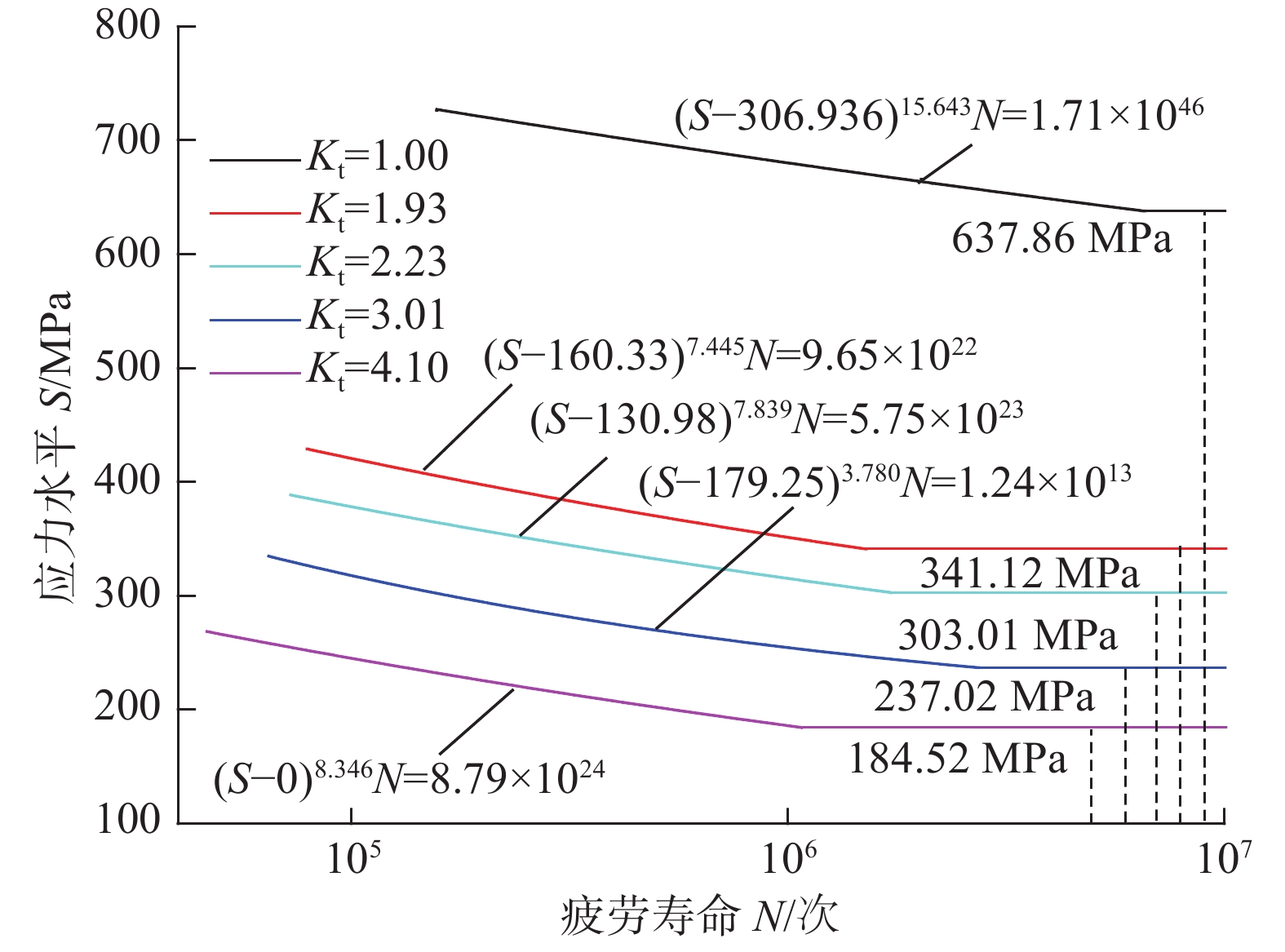
试样类型	$\scriptstyle R$ /mm	$\scriptstyle K_{\rm{t}}$	$\scriptstyle S_{{\rm{ - 1}}}^{\rm{e}}/ {\rm{MPa}}$	$\scriptstyle K_{\rm{f}}$	$\scriptstyle q$
光滑	∞	1.00	637.85	1.00	0
缺口	0.6	1.93	341.12	1.87	0.94
	0.4	2.23	303.01	2.10	0.90
	0.2	3.01	237.01	2.69	0.84
	0.1	4.11	184.51	3.46	0.79

下载: 导出CSV

参考文献(18)

[1]	HUANG Bensheng, YANG Jiang, ZHANG Hui, et al. Influence of H₂S corrosion on rotating bending fatigue properties of S135 drill pipe steel[J]. Transactions of the Indian Institute of Metals, 2018, 71(1): 1–9. doi: 10.1007/s12666-017-1135-5
[2]	ZENG Dezhi, TIAN Gang, HU Junying, et al. Effect of immersion time on the mechanical properties of S135 drill pipe immersed in H₂S solution[J]. Journal of Materials Engineering and Performance, 2014, 23(11): 4072–4081. doi: 10.1007/s11665-014-1198-y
[3]	OJANOMARE C, CORNETTI P, ROMAGNOLI R A. Fatigue crack growth analysis of drill pipes during rotary drilling operations by the multiple reference state weight function approach[J]. Engineering Failure Analysis, 2017, 74: 11–34. doi: 10.1016/j.engfailanal.2016.12.013
[4]	LIU Yonggang, LIAN Zhanghua, LIN Tiejun, et al. A study on axial cracking failure of drill pipe body[J]. Engineering Failure Analysis, 2016, 59: 434–443. doi: 10.1016/j.engfailanal.2015.11.004
[5]	ZAMANI S M, HASSANZADEH-TABRIZI S A, SHARIFI H. Failure analysis of drill pipe: a review[J]. Engineering Failure Analysis, 2016, 59: 605–623. doi: 10.1016/j.engfailanal.2015.10.012
[6]	LIN Yuanhua, ZHU Dajiang, ZENG Dezhi, et al. Numerical and experimental distribution of stress fields for double shoulder tool joint[J]. Engineering Failure Analysis, 2011, 18(6): 1584–1594. doi: 10.1016/j.engfailanal.2011.06.003
[7]	LIN Yuanhua, LI Qiang, SUN Yongxing, et al. A repeated impact method and instrument to evaluate the impact fatigue property of drill pipe[J]. Journal of Materials Engineering & Performance, 2013, 22(4): 1064–1071.
[8]	LIN Yuanhua, QI Xing, ZHU Dajiang, et al. Failure analysis and appropriate design of drill pipe upset transition area[J]. Engineering Failure Analysis, 2013, 31(31): 255–267.
[9]	林元华,潘杰,刘婉颖,等. 硫化氢环境下G–105 和S–135 钻杆的低载多冲疲劳性能测试[J]. 石油钻采工艺, 2016, 38(1): 59–63. LIN Yuanhua,PAN Jie,LIU Wanying,et al. Low-load repeated impact testing of G-105 and S-135 drill pipes in H₂S environ-ment[J]. Oil Drilling & Production Technology, 2016, 38(1): 59–63.
[10]	HAN Yan, ZHAO Xuehu, BAI Zhenquan, et al. Failure analysis on fracture of a S135 drill pipe[J]. Procedia Materials Science, 2014, 3: 447–453. doi: 10.1016/j.mspro.2014.06.075
[11]	LU Shuanlu, FENG Yaorong, LUO Faqian, et al. Failure analysis of IEU drill pipe wash out[J]. International Journal of Fatigue, 2005, 27(10/11/12): 1360–1365.
[12]	SHATSHATS'KYI I P, LYSKANYCH O M, KORNUTA V A. Combined deformation conditions for fatigue damage indicator and well-drilling tool joint[J]. Strength of Materials, 2016, 48(3): 469–472. doi: 10.1007/s11223-016-9786-8
[13]	N'DIAYE A, HARIRI S, PLUVINAGE G, et al. Stress concentration factor analysis for notched welded tubular T-joints[J]. International Journal of Fatigue, 2007, 29(8): 1554–1570. doi: 10.1016/j.ijfatigue.2006.10.030
[14]	ZUCUNI C P, GUILARDI L F, FRAGA S, et al. CAD/CAM machining vs pre-sintering in-lab fabrication techniques of Y-TZP ceramic specimens: effects on their mechanical fatigue behavior[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2017, 71: 201–208. doi: 10.1016/j.jmbbm.2017.03.013
[15]	FRAGA S, PEREIRA G K R, FREITAS M A, et al. Loading frequencies up to 20 Hz as an alternative to accelerate fatigue strength tests in a Y-TZP ceramic[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2016, 61: 79–86. doi: 10.1016/j.jmbbm.2016.01.008
[16]	WAN Aoshuang, XIONG Junjiang, LYU Zhiyang, et al. High-cycle fatigue behavior of Co-based superalloy 9CrCo at elevated temperatures[J]. Chinese Journal of Aeronautics, 2016, 29(5): 1405–1413. doi: 10.1016/j.cja.2016.01.009
[17]	EWEST D, ALMROTH P, SJODIN B, et al. A modified compliance method for fatigue crack propagation applied on a single edge notch specimen[J]. International Journal of Fatigue, 2016, 92(1): 61–70.
[18]	束德林. 工程材料力学性能[M]. 3版. 北京: 机械工业出版社, 2017. SHU Delin. Mechanical properties of engineering materials[M]. 3rd ed. Beijing: Mechanical Industry Press, 2017.

施引文献(1)

期刊类型引用(1)

端祥刚，胡志明，常进，石雨昕，吴振凯，许莹莹. 页岩储层无支撑缝网区流动能力影响因素研究与进展. 特种油气藏. 2025(01): 22-31 .

百度学术

其他类型引用(0)

资源附件(0)

图(13) / 表(2)

计量

文章访问数: 12082
HTML全文浏览量: 6378
PDF下载量: 109
被引次数: 1

1. 页岩自吸中的水化结构损伤特征
1.1 水化结构损伤
1.2 结构损伤定量表征
2. 页岩自吸动态毛细管力与迂曲度分析
2.1 动态毛细管力分析
2.2 动态迂曲度分析
3. 页岩动态自吸物理模型
3.1 自吸模型构建
3.2 自吸模型验证
3.3 模型对比分析
4. 页岩自吸影响因素分析
5. 结　论

1. 页岩自吸中的水化结构损伤特征
1.1 水化结构损伤
1.2 结构损伤定量表征
2. 页岩自吸动态毛细管力与迂曲度分析
2.1 动态毛细管力分析
2.2 动态迂曲度分析
3. 页岩动态自吸物理模型
3.1 自吸模型构建
3.2 自吸模型验证
3.3 模型对比分析
4. 页岩自吸影响因素分析
5. 结　论

参考文献(18)

施引文献(1)

资源附件(0)

S135钻杆接头缺口疲劳行为研究

作者简介: 李皓（1988—），男，甘肃陇南人，2011年毕业于兰州城市学院石油工程专业，2018年获西南石油大学油气井工程专业硕士学位，主要从事油气设施腐蚀与防护工作。E-mail：lihao1477024473@163.com

通讯作者: 曾德智，zengdezhi1980@163.com

计量

出版历程

A Study of the Notch Fatigue Behavior of S135 Drill Pipe Joint

1. 页岩自吸中的水化结构损伤特征

1.1 水化结构损伤

1.2 结构损伤定量表征

2. 页岩自吸动态毛细管力与迂曲度分析

2.1 动态毛细管力分析

2.2 动态迂曲度分析

3. 页岩动态自吸物理模型

3.1 自吸模型构建

3.2 自吸模型验证

3.3 模型对比分析

4. 页岩自吸影响因素分析

5. 结 论

期刊类型引用(1)

其他类型引用(0)

计量

出版历程

目录

1. 页岩自吸中的水化结构损伤特征

1.1 水化结构损伤

1.2 结构损伤定量表征

2. 页岩自吸动态毛细管力与迂曲度分析

2.1 动态毛细管力分析

2.2 动态迂曲度分析

3. 页岩动态自吸物理模型

3.1 自吸模型构建

3.2 自吸模型验证

3.3 模型对比分析

4. 页岩自吸影响因素分析

5. 结 论

作者简介:
李皓（1988—），男，甘肃陇南人，2011年毕业于兰州城市学院石油工程专业，2018年获西南石油大学油气井工程专业硕士学位，主要从事油气设施腐蚀与防护工作。E-mail：lihao1477024473@163.com

通讯作者:
曾德智，zengdezhi1980@163.com

5. 结　论

5. 结　论