超深纹层页岩断裂韧性演化规律研究

燕鸣飞; 金衍; 韦世明; 夏阳; 陈勉

doi:10.11911/syztjs.2025032

超深纹层页岩断裂韧性演化规律研究

燕鸣飞^{1, 2,},
金衍^{1, 2, ,},
韦世明^{1, 2},
夏阳^{1, 2},
陈勉^{1, 2}

1.
中国石油大学（北京）石油工程学院，北京 102249
2.
油气资源与工程全国重点实验室（中国石油大学（北京）），北京 102249

基金项目: 国家自然科学基金重点项目“提高超深大斜度井压裂效率的关键力学问题研究”（编号：52334001），国家自然科学基金青年项目“缝洞型碳酸盐岩大斜度井裂缝非平面扩展机理研究”（编号：42407252），中国石油大学（北京）青年拔尖人才项目“超深层近井裂缝扩展转向流固耦合力学机理研究”（编号：2462023BJRC007）联合资助。

详细信息

作者简介:
燕鸣飞（1997—），男，山西临汾人，2020年毕业于中国石油大学（北京）石油工程专业，在读博士研究生，主要从事岩石力学与井壁稳定方面的研究工作。E-mail：15611788113@163.com

通讯作者:
金衍，jiny@cup.edu.cn

中图分类号: TE311⁺.2
计量
- 文章访问数: 80
- HTML全文浏览量: 16
- PDF下载量: 34
出版历程
- 收稿日期: 2023-12-20
- 修回日期: 2025-03-01
- 网络出版日期: 2025-03-25
- 刊出日期: 2025-04-27

Study on Evolution Law of Fracture Toughness of Ultra-Deep Laminated Shale

YAN Mingfei^{1, 2,},
JIN Yan^{1, 2, ,},
WEI Shiming^{1, 2},
XIA Yang^{1, 2},
CHEN Mian^{1, 2}

1.
College of Petroleum Engineering, China University of Petroleum (Beijing), Beijing, 102249, China
2.
National Key Laboratory of Petroleum Resources and Engineering, China University of Petroleum (Beijing), Beijing, 102249, China

摘要

摘要:
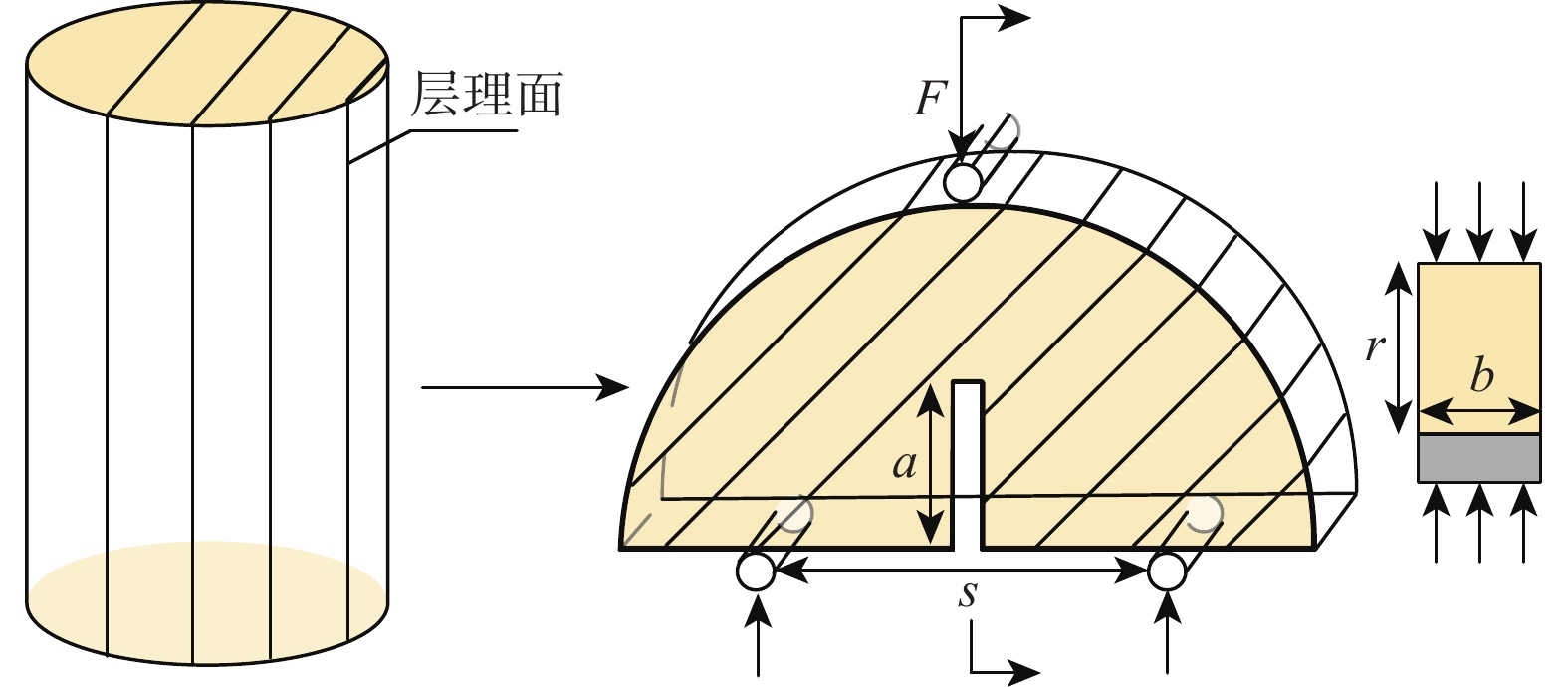
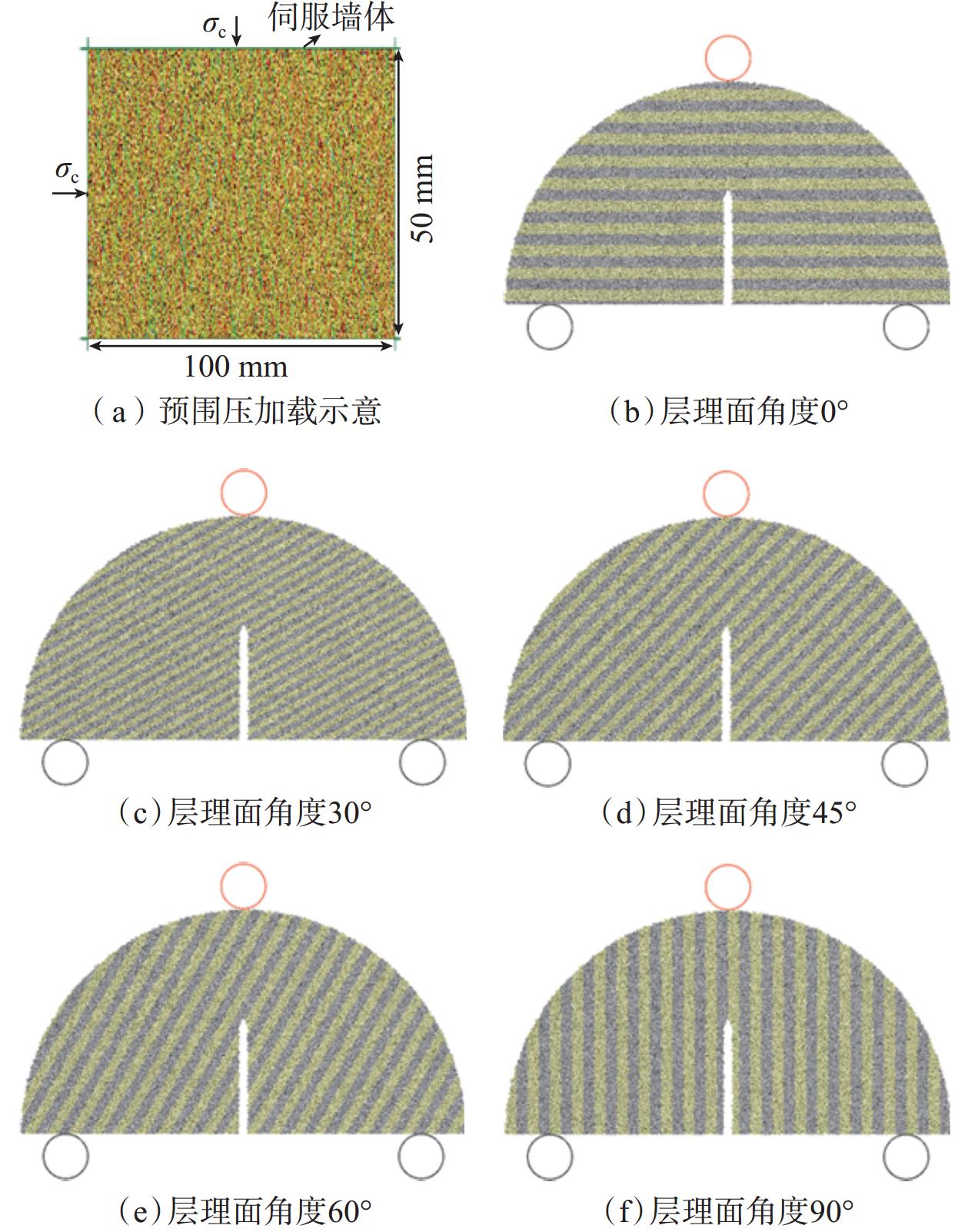
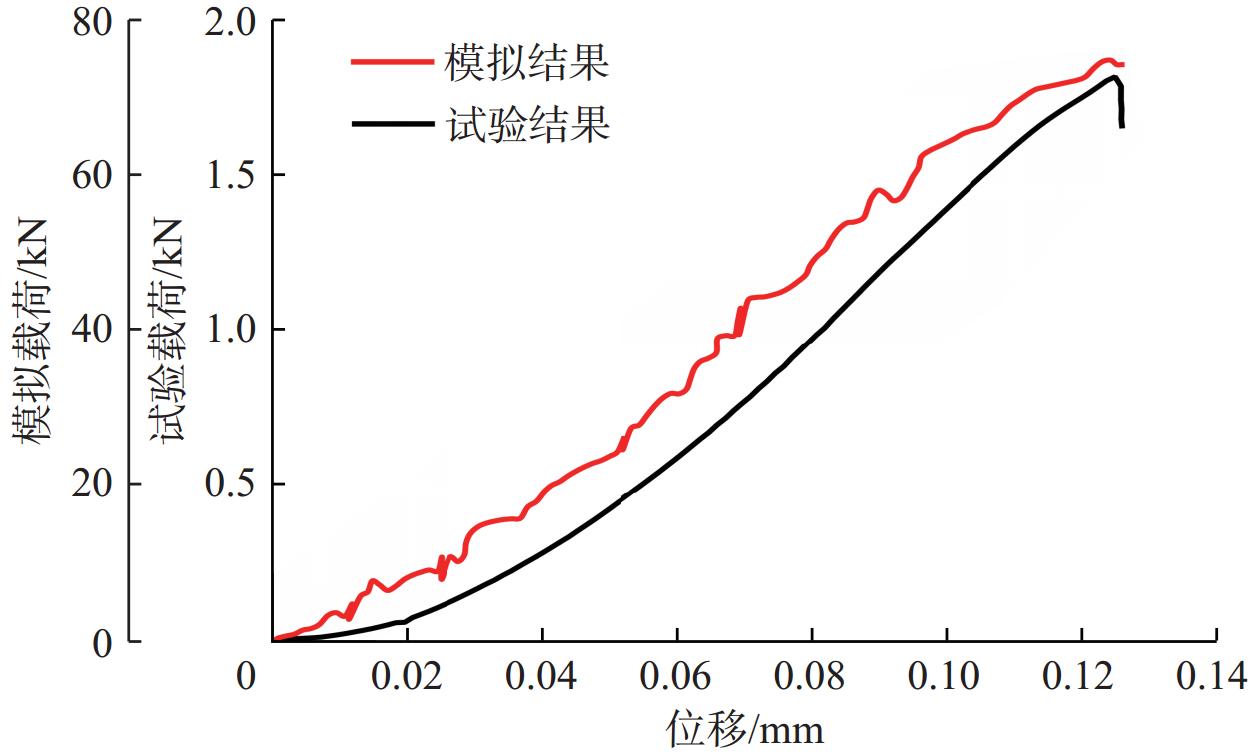
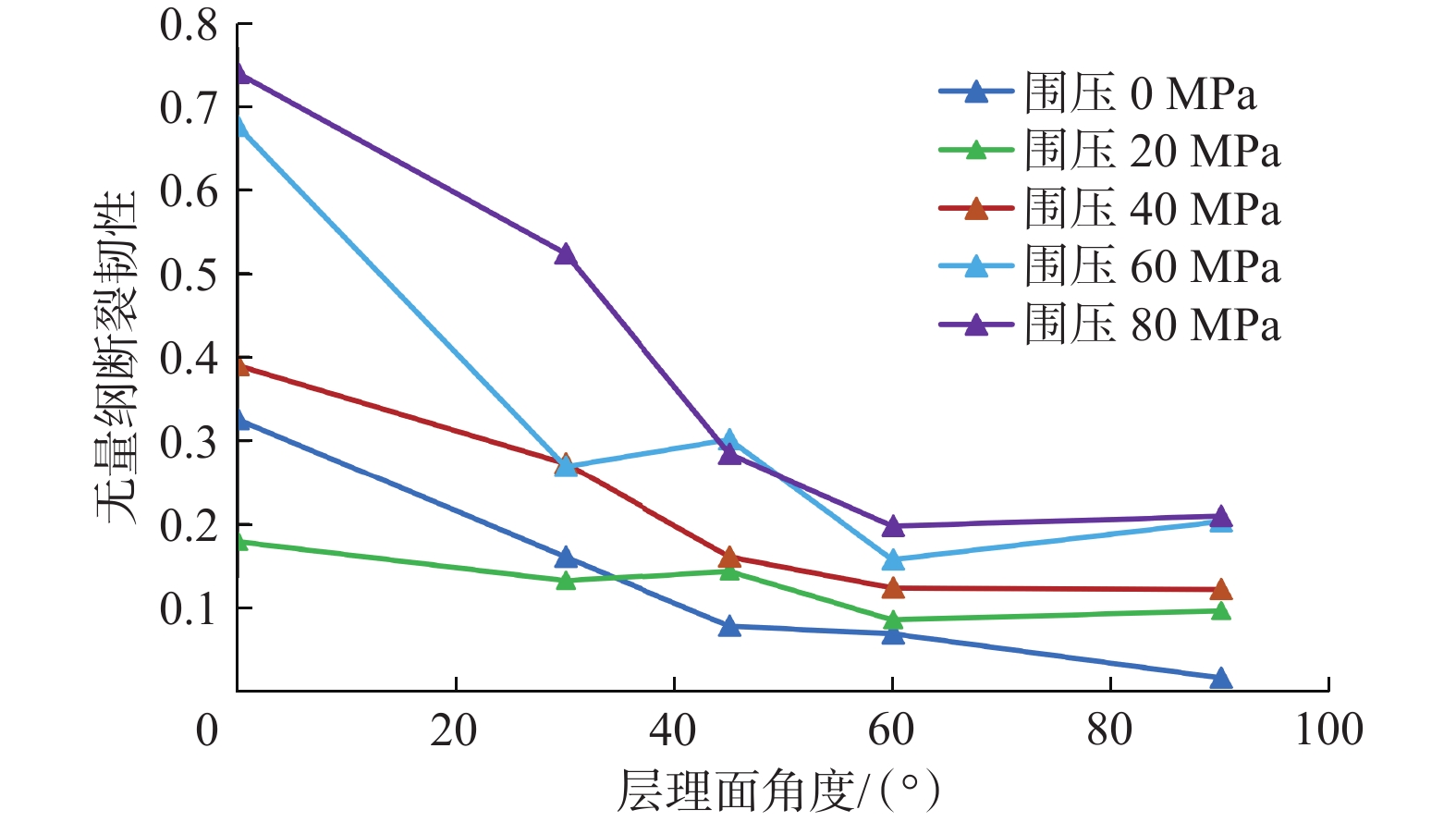
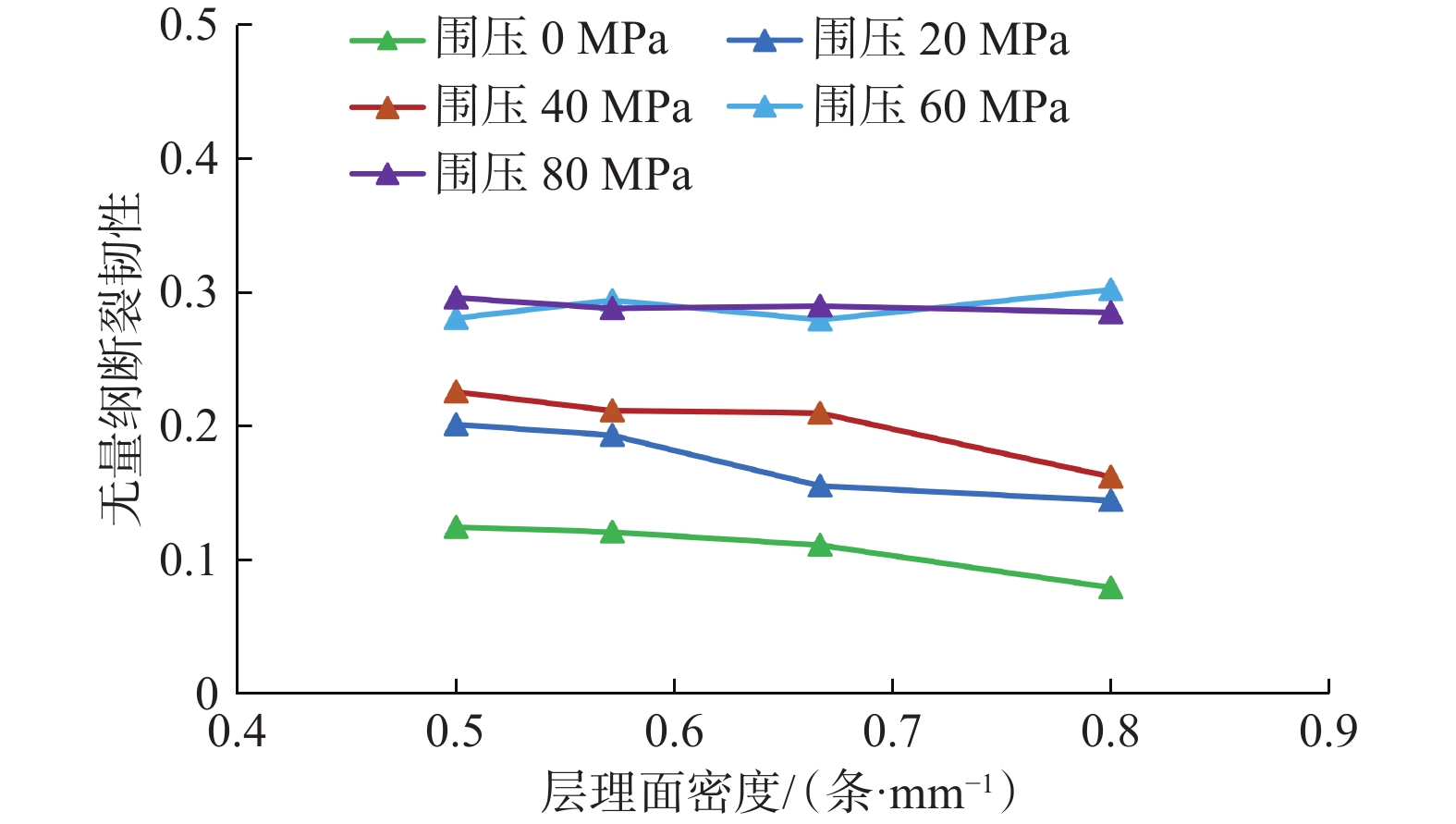
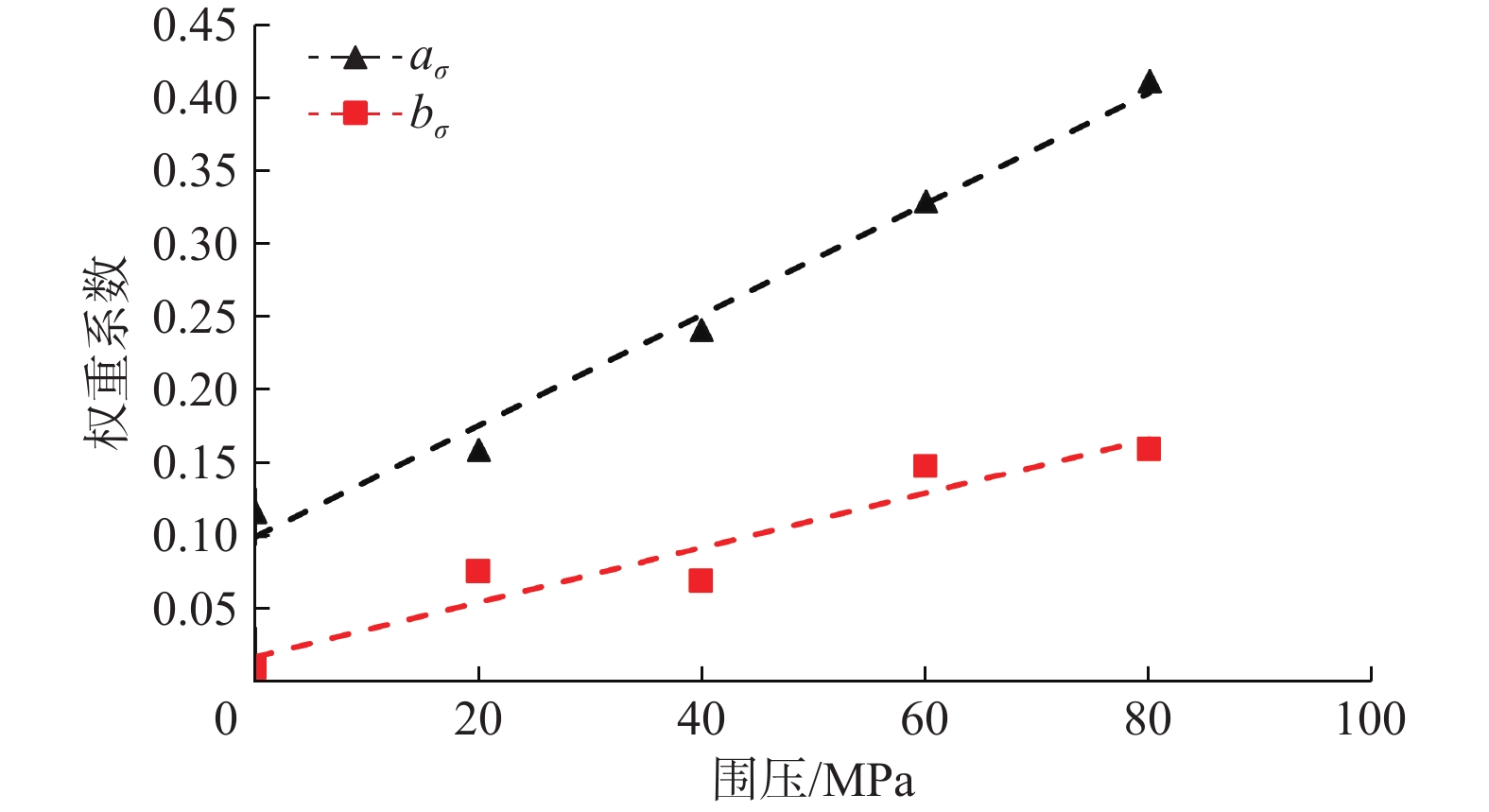
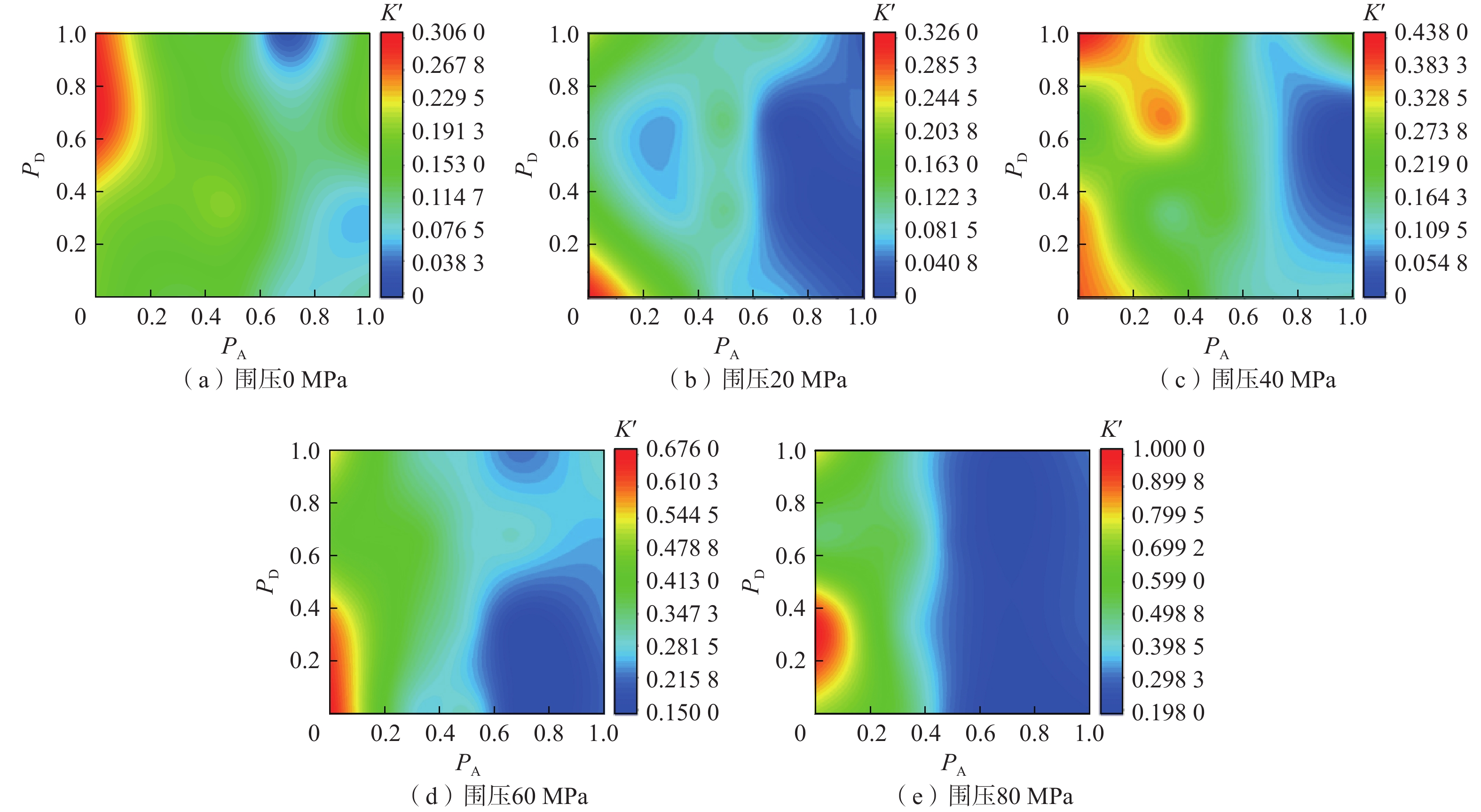
为深入探究超深页岩储层中水力裂缝纵向穿层机制，针对高应力及层理性质对页岩断裂特性的影响进行了系统性分析。首先，利用三轴压缩试验获取了页岩力学参数；其次，采用颗粒离散元法构建了带围压的半圆板页岩三点弯曲数值模型，模拟了页岩在不同工况下的断裂过程。数值模拟结果表明，围压增大显著提升了页岩的断裂韧性，且层理面角度和密度对断裂韧性的影响随着围压增大而增强：相同围压下，断裂韧性随着层理面角度增加而降低，随着层理面密度增加呈现小幅差异，表明层理面密度对断裂韧性的强化作用优于层理面角度。基于此，拟合了断裂韧性与围压、层理面角度和密度的定量关系，并构建了不同围压及层理面性质对页岩断裂韧性的量化图版。研究结果揭示了高应力条件下超深页岩储层层理性质对断裂特性的复杂影响，为优化水力压裂方案、有效控制水力裂缝穿层行为提供了理论依据。
- 超深页岩 /
- 高应力 /
- 层理面 /
- 断裂韧性 /
- 颗粒流方法
Abstract:
To explore the longitudinal hydraulic fracture propagation mechanism in ultra-deep shale reservoirs, the influence of high stress and bedding properties on shale fracture characteristics was systematically analyzed. Initially, shale mechanical parameters were obtained through triaxial compression experiments. Subsequently, a three-point bending numerical model of a semi-circular shale plate with confining pressure was constructed using the particle discrete element method to simulate the shale fracture process under various conditions. The numerical simulation results demonstrate that increasing the confining pressure significantly enhances shale fracture toughness, and the influence of bedding plane angle and density on fracture toughness is amplified with increasing confining pressure. At the same confining pressure, fracture toughness decreases with an increase in bedding plane angle and exhibits a minor variation with an increase in bedding plane density, indicating that bedding plane density has a greater strengthening effect on fracture toughness than bedding plane angle. Based on these findings, the quantitative relationship of fracture toughness with confining pressure, bedding plane angle, and density was fitted, and a quantitative chart illustrating the impact of varying confining pressures and bedding plane properties on shale fracture toughness was developed. The results reveal the complex influence of bedding properties on fracture characteristics under high stress conditions in ultra-deep shale reservoirs, providing a theoretical basis for optimizing hydraulic fracturing schemes and effectively controlling hydraulic fracture propagation behavior.
- ultra-deep shale /
- high stress /
- bedding plane /
- fracture toughness /
- particle flow method

HTML全文

页岩油气储层致密，能量保持难、流动阻力大，大规模压裂改造是其高效开发的主要技术手段^[1-5]。东营凹陷陆相页岩油资源量丰富，亟需采用新技术实现高效开发^[6-7]。超临界CO₂具有低黏度、高渗透、低表面张力的物理特性，被认为是非常规储层改造新方法之一^[8-10]。然而，超临界CO₂压裂的相态和物理性质复杂，造缝机理尚不清楚，学者们多采用试验和数值模拟方法开展相关研究^[11-15]。试验表明，CO₂可降低破裂压力^[16]，超临界CO₂压裂形成的裂缝表面相对于滑溜水压裂产生的裂缝表面更为粗糙^[17]，使用超临界CO₂在降低岩石破裂压力和造缝方面具有很大的优势^[18]。目前，相关研究多针对CO₂低黏度特性对压裂的影响，对CO₂对岩石物性影响的关注较少。此外，CO₂压裂裂缝形态复杂，传统方法模拟裂缝多为单缝结构，采用现的数值模拟手段难以精确刻画前置CO₂压裂缝网^[19-21]。

赵辉等人^[22-24]提出了基于闪电模拟的油藏压裂模型，可以很好地表征裂缝复杂性，但仅适用于水力压裂，未考虑压裂过程中CO₂对裂缝扩展形态的影响。借鉴该方法，笔者考虑CO₂的相态变化特征及CO₂对岩石性质的影响，结合物理试验和数值模拟，提出了基于节点连接方法（NCM）的CO₂增能压裂裂缝扩展模拟模型，在此基础上进一步讨论了前置CO₂比例、地质参数、物性参数及压裂施工参数对裂缝形态的影响，并在东营凹陷陆相页岩油X井开展分析应用。

1. CO₂增能压裂裂缝扩展模拟模型

1.1 CO₂岩石压裂起裂压力与应力变化表征

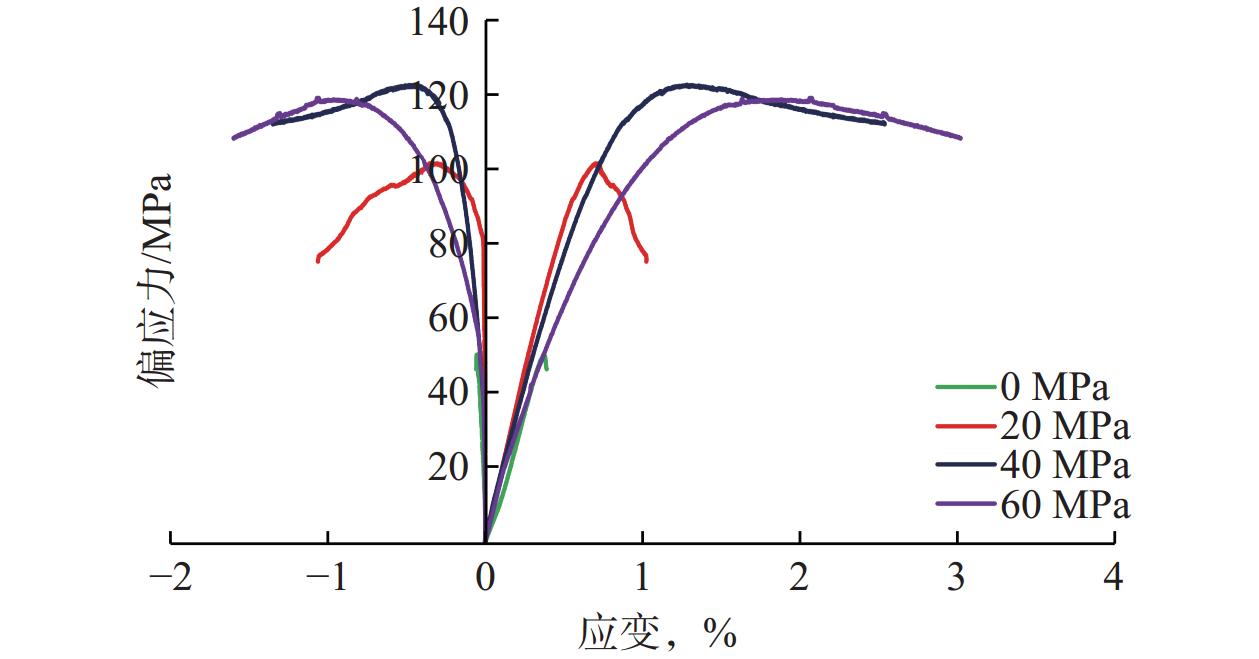
为准确表征胜利油田东营凹陷陆相页岩经过CO₂浸泡后的岩石力学与破裂特征，选取2口典型井12块岩样，利用岩石力学仪测试其不同CO₂浸泡时间下和不同围压下的强度、弹性模量、泊松比、内聚力等岩石力学参数，结合破裂压力剪切压力等计算公式，发现东营凹陷陆相页岩油岩体破裂压力、天然裂缝剪切及张开应力和地应力随CO₂浸泡时间增长呈现线性降低的趋势（见图1）。

图 1 页岩破裂压力与应力随CO₂浸泡时间的变化

Figure 1. Initiation pressure and stress changes during CO₂ fracturing in rock

下载: 全尺寸图片幻灯片

1.2 CO₂物性参数变化表征

前置CO₂注入过程中，随着温度和压力条件变化，CO₂的密度和黏度均会发生显著变化，影响压裂裂缝扩展。采用Pen-Robinson方程刻画CO₂密度变化，其状态方程可表示为^[25]：

$p = \frac{{8.314T}}{{V - 26.667}} - \frac{{396\text{ }306.77 {{[1 + 0.707\text{ }979(1 - \sqrt {{T_{\text{r}}}} )]}^2}}}{{V(V + 26.667) + 26.667(V - 26.667)}}$

(1)

式中：T为CO₂的绝对温度，K；V为CO₂的摩尔体积，L/mol；T_r为对比温度，即CO₂绝对温度T与临界温度T_c（T_c=304.13K）之比。

根据式（1）确定CO₂的体积后，即可进一步获得CO₂在该温度和压力条件下的密度。

CO₂黏度与温度的关系^[21]为：

$\mu = \frac{{36.344\left[ {\dfrac{{\sqrt {1.259\text{ }3{T_{\text{r}}}} }}{{{\Omega _{\text{u}}}}} {{F_{\text{c}}} \left(\dfrac{1}{{{G_2}}} + {E_6}\dfrac{{c {V_{\text{e}}}}}{6}\right)} + {\eta ^{{\text{**}}}}} \right]\sqrt {M{T_{\text{c}}}} }}{{\sqrt[3]{{V_{\text{c}}^2}}}}$

(2)

其中，部分系数定义为：

${F_{\text{c}}} = 1 - 0.275\text{ }6\omega + 0.059\text{ }035\mu _{\text{r}}^4 + \kappa$

(3)

${\eta ^{{\text{**}}}} = {E_7}{y^2}{G_2}\exp \left({E_8} + \frac{{{E_9}}}{{{T^*}}} + \frac{{{E_{10}}}}{{{T^*}^2}}\right)$

(4)

${G_2} = \frac{{\dfrac{{{E_1}[ 1 - \exp ( - {E_4}y)]}}{y} + {E_2}\dfrac{{1 - 0.5y}}{{{{(1 - y)}^3}}}\exp ({E_5}y) - {E_3}\dfrac{{1 - 0.5y}}{{{{(1 - y)}^3}}}}}{{{E_1}{E_4} + {E_2} + {E_3}}}$

(5)

${E_i} = {f_i}(\omega ,\kappa )$

(6)

式中：T_r为临界温度，K；F_c为形状和极性因子；V_e为气体体积，m³；ω为偏心因子；y为摩尔分数；T*为绝对温度，K；M为摩尔质量，g/mol；V_c为CO₂的临界体积，m³；Ω_u为碰撞积分；μ_r为约化偶极矩；κ为高极性物质的关联因子；c为单位体积物质的量，mol/m³。

1.3 基于NCM的CO₂增能压裂裂缝扩展数学模型

基于节点体系扩展模拟方法（Node Connection Method, NCM）^[22-23]，考虑前置CO₂注入后对岩石力学、物性参数的影响，构建前置CO₂增能压裂裂缝扩展模拟模型。

1.3.1 前置CO₂水力压裂力学机制

假设岩石为多孔弹性介质，根据测井资料获取地层物性参数，以三维弹性理论为基础，可以得到地下水平主应力的计算方法。结合试验研究结果，储层中岩石的泊松比、弹性模量等参数会随着CO₂浸泡时间增长而变化，在模型中需要考虑。因此，水平主应力与时间的关系可以表示为：

$\left\{ \begin{array}{*{20}{l}} \sigma _{_\text{h}}^t = \dfrac{{{\nu ^t}}}{{1 - {\nu ^t}}}{\sigma _\text{v}} - \dfrac{{{\nu ^t}}}{{1 - {\nu ^t}}}{\alpha _\text{v}}{p_\text{p}} + {\alpha _\text{h}}{p_\text{p}} + \dfrac{{{E^t}}}{{1 - {{({\nu ^t})}^2}}}{\xi _\text{h}} + \\ \qquad \dfrac{{{\nu ^t}{E^t}}}{{1 - {{({\nu ^t})}^2}}}{\xi _\text{H}} \\ \sigma _{_\text{H}}^t = \dfrac{{{\nu ^t}}}{{1 - {\nu ^t}}}{\sigma _\text{v}} - \dfrac{{{\nu ^t}}}{{1 - {\nu ^t}}}{\alpha _\text{v}}{p_\text{p}} + {\alpha _\text{H}}{p_\text{p}} + \dfrac{{{E^t}}}{{1 - {{({\nu ^t})}^2}}}{\xi _\text{H}} +\\ \qquad \dfrac{{\nu {E^t}}}{{1 - {{({\nu ^t})}^2}}}{\xi _\text{h}} \end{array} \right.$

(7)

式中：σ^t_h为t时刻的最小水平主应力，MPa；σ^t_H为t时刻的最大水平主应力，MPa；σ_v为垂向应力，MPa；α_v、α_h为垂向和水平的Biot系数；ξ_H、ξ_h为最大水平主应力和最小水平主应力的应变系数；ν^t为t时刻泊松比；E^t为t时刻的弹性模量，GPa；p_p为孔隙压力，MPa。

压裂过程中，新生缝会改变岩石的力学状态，影响后续裂缝扩展，简称应力阴影效应。采用诱导应力解析解和叠加原理描述全局应力状态^[26]：

$\left\{ {\begin{array}{*{20}{c}} \sigma _{xx}^{t + 1}(i,j) = \sigma _{xx}^t(i,j) +\\ \quad\displaystyle \sum\limits_{m = 1}^N {{p_{\text{n},m}}\left( {\dfrac{{{L_m}}}{{\sqrt {{L_{1,m}}{L_{2,m}}} }}\cos \dfrac{{2{\theta _m} - {\theta _{1,m}} - {\theta _{2,m}}}}{2} - 2} \right)} - \\ \quad{ \displaystyle\sum\limits_{m = 1}^N {{p_{\text{n},m}}\dfrac{{{L_m}}}{a}{{\left( {\dfrac{{{a^2}}}{{{L_{1,m}}{L_{2,m}}}}} \right)}^{3/2}}\sin {\theta _m}\sin {\dfrac{3}{2}\left( {{\theta _{1,m}} + {\theta _{2,m}}} \right)} } } \\ \sigma _{yy}^{t + 1}(i,j) = \sigma _{yy}^t(i,j) +\\ \quad\displaystyle\sum\limits_{m = 1}^N {{p_{\text{n},m}}\left( {\dfrac{{{L_m}}}{{\sqrt {{L_{1,m}}{L_{2,m}}} }}\cos \dfrac{{2{\theta _m} - {\theta _{1,m}} - {\theta _{2,m}}}}{2} - 2} \right)} +\\ \quad{ \displaystyle \sum\limits_{m = 1}^N {{p_{\text{n},m}}\dfrac{{{L_m}}}{a}{{\left( {\dfrac{{{a^2}}}{{{L_{1,m}}{L_{2,m}}}}} \right)}^{3/2}}\sin {\theta _m}\sin {\dfrac{3}{2}\left( {{\theta _{1,m}} + {\theta _{2,m}}} \right)} } } \\ \tau _{xy}^{t + 1}(i,j) = \tau _{xy}^t(i,j) + \displaystyle\sum\limits_{m = 1}^N {p_{net,m}}\dfrac{{{L_m}}}{a}{{\left( {\dfrac{{{a^2}}}{{{L_{1,m}}{L_{2,m}}}}} \right)}^{3/2}}\cdot\\ \quad\sin {\theta _m}\cos {\dfrac{3}{2}\left( {{\theta _{1,m}} + {\theta _{2,m}}} \right)} \end{array}} \right.$

(8)

式中：σ^t+1_xx和σ^t_xx分别为t+1和t时间步下(i, j)位置处x轴向主应力，MPa；σ^t+1_yy和σ^t_yy分别为t+1和t时间步下(i, j)位置处y轴向主应力，MPa；τ^t+1_xy和τ^t_xy分别为t+1和t时间步下(i, j)位置处剪切应力，MPa；N为裂缝微元数量；p_n,m为裂缝m微元的缝内净压力，MPa；a为裂缝微元半长，m；L_m，L_1,m和L_2,m为位置(i, j)到裂缝m微元的距离，m；θ_m，θ_1,m和θ_2,m为位置(i, j)到裂缝m微元的角度。

对裂缝内流体流动简化处理，不考虑裂缝在缝宽方向上的流动过程，且裂缝壁面上的流速为0，则流体在裂缝内为一维流动。对流体压降方程进行处理，可得到缝内压力分布为：

$p_{i,m}^t = - \frac{{12\mu _m^t{q_m}{x_m}}}{{{h_{\text{f},m}}w_m^3}} + {p_0}$

(9)

式中：p^t_i,m为t时间步时裂缝m微元的净压力，MPa；μ^t_m为t时间步时裂缝m微元中流体的黏度，mPa·s；q_m为裂缝m微元的流量；x_m为裂缝m微元与井筒的距离，m；h_f,m为裂缝m微元的高度，m；p₀为初始压力，MPa。

对于前置CO₂压裂，裂缝内流体黏度随着CO₂性质而改变，采用式（2）修正不同时间步下前置CO₂的黏度。

将临界起裂应力作为起裂判据，该值与岩石断裂韧性有关，则裂缝扩展条件为^[23]：

${\sigma _{\text{fr}}} = \frac{1}{{\sqrt {2\text{π} r} }}\cos \frac{\theta }{2}\left( {{K_1}{{\cos }^2}\frac{\theta }{2} - \frac{3}{2}{K_2}\sin \theta } \right) - {\sigma _{\text{cr}}} \geqslant 0$

(10)

式中：σ_fr为残余起裂应力，MPa；σ_cr为临界起裂应力，MPa；K₁为Ⅰ型应力强度因子，MPa·m^0.5；K₂为Ⅱ型应力强度因子，MPa·m^0.5。

分支裂缝密度表示为在裂缝的改造范围内共有的裂缝节点数量，其计算公式为：

${\rho }_{\text{if}}=\frac{{n}}{{L}_{\text{f}}{w}_{\text{f}}}$

(11)

式中：ρ_if为分支缝密度，条/m²；n为裂缝节点数量；L_f为裂缝长度，m；w_f为裂缝的带宽，m。

1.3.2 前置CO₂压裂模拟流程

基于NCM的CO₂增能压裂裂缝扩展模型计算流程如图2所示。具体步骤为：1）依据实际储层大小划分地质单元，作为计算的离散体；2）结合地质资料给地质单元赋值；3）根据实际压裂规模，设置射孔参数；4）计算现存裂缝单元缝内流体压力分布；5）结合应力阴影效应及缝内流体流动特征，校正储层应力分布；6）计算裂缝尖端周向应力和临界起裂应力；7）判断是否存在满足起裂条件的裂缝单元，不满足时输出裂缝形态；8）引入随机函数及概率分布，确定新的裂缝单元；9）根据CO₂物性的变化，更新缝内流体物性参数；10）重复步骤4）—9），直至输出裂缝形态。

图 2 CO₂前置增能压裂扩展模拟流程

Figure 2. Simulation process of CO₂ pre-energized fracturing

下载: 全尺寸图片幻灯片

2. 前置CO₂增能压裂裂缝扩展模拟

选用胜利油田东营凹陷陆相页岩油储层地质力学参数以及物性参数，基于构建模型，分析不同影响因素下裂缝扩展形态。模型尺寸大小为160 m×300 m，1段射孔3簇，射孔点在模型中间位置处，模拟裂缝排量为16 m³/min，页岩基质的弹性模量为26.36 GPa，泊松比为0.30。

2.1 前置CO₂比例对缝网形态的影响

模拟前置CO₂比例分别为0.1、0.2和0.3时的裂缝形态（见图3），分析不同前置CO₂比例与裂缝长度缝网带宽及分支缝密度的关系（见图4）。

图 3 不同CO₂比例下的裂缝形态

Figure 3. Fracture morphology under different CO₂ ratios

下载: 全尺寸图片幻灯片

图 4 不同CO₂比例对裂缝参数的影响

Figure 4. Influence of different CO₂ ratios on fracture parameters

下载: 全尺寸图片幻灯片

前置CO₂比例对整体缝网扩展长度影响最大，前置CO₂比列由0.1增至0.3时，缝网长度缩短近40%。压裂缝网带宽主要受压裂簇数影响，前置CO₂比例对整体缝网扩展带宽影响较小。前置CO₂比例对分支缝密度的影响很大，当前置CO₂比例由0.1增加至0.3时，分支缝网密度由0.06 条/m²增加至0.13 条/m²，增加了117%。这主要是因为超临界CO₂易于进入基质孔隙和微裂隙中，促进了基质的破裂和微裂隙的开启，增加了分支裂缝的数量，形成了复杂的网状裂缝形态。

2.2 水平应力差对裂缝形态的影响

模拟水平应力差分别为0，15和30 MPa时的裂缝形态（见图5），分析不同水平应力差与裂缝长度缝网带宽及分支缝密度的关系（见图6）。

图 5 不同应力差下的裂缝形态

Figure 5. Fracture morphology under different stress differences

下载: 全尺寸图片幻灯片

图 6 储层应力差对裂缝参数的影响

Figure 6. Influence of reservoir stress difference on fracture parameters

下载: 全尺寸图片幻灯片

应力差与缝长相关性很大，与缝宽相关性较小，与分支缝密度相关性大，应力差主要影响缝长及分支缝密度。水平应力差由5 MPa增至30 MPa时，裂缝长度由175 m增至266 m，缝网带宽由63 m降至58 m，降低了3.18%，分支缝密度由0.095 条/m²降至0.074 条/m²，下降了31.85%。相较于滑溜水压裂，前置CO₂增能压裂在高应力差下依然可以形成复杂裂缝网。因此，高应力差储层采用前置CO₂进行压裂，可以提高压裂改造效果，实现高效增产。

2.3 储层渗透率对裂缝形态的影响

模拟储层渗透率分别为0.05，0.5和5 mD时的裂缝形态（见图7），分储层渗透率与裂缝长度、缝网带宽及分支缝密度的关系（见图8）。结果发现，储层渗透率对裂缝长度和带宽的影响较小，对分支缝密度的影响较大。总体而言，储层渗透率影响压裂流体的滤失性，前置CO₂压裂对于储层渗透率的敏感程度要远大于滑溜水压裂。其原因在于，储层渗透率影响CO₂向基质的滤失量和波及范围，对于开启天然裂缝和储层增压作用明显。因此，对于高渗透储层，应适当增大排量和压裂液量，从而增大压裂改造范围。

图 7 不同渗透率下的裂缝形态

Figure 7. Fracture morphology under different permeability

下载: 全尺寸图片幻灯片

图 8 储层渗透率对裂缝参数的影响

Figure 8. Influence of reservoir permeability on fracture parameters

下载: 全尺寸图片幻灯片

3. 实例分析

东营凹陷陆相页岩油X井目的层为沙四上纯上3层组，水平段长度1 976 m，钻遇岩相以泥质灰页岩（970 m）、灰质泥页岩（550 m）为主；前置CO₂增能压裂完成34段、120簇压裂施工，平均3.5 簇/段，加砂4 300.6 m³（设计4 204.7 m³）、注入携砂液73 166 m³，平均单段加砂126.5 m³、加砂强度2.4 m³/m。结合实际施工参数模拟裂缝扩展形态，X井36段反演裂缝平均缝长为277.80 m，平均缝宽为59.85 m。X井压裂时的微地震监测结果见图9，裂缝扩展模拟结果见图10。

图 9 X井压裂时的微地震监测结果

Figure 9. Microseismic monitoring results of fracturing of Well X

下载: 全尺寸图片幻灯片

图 10 X井裂缝形态整体反演效果

Figure 10. Overall inversion effect of fracture morphology of Well X

下载: 全尺寸图片幻灯片

X 井压裂过程中进行单井尺度模拟时，由于模拟布点精度及显示尺度的原因，裂缝整体上呈双翼对称复杂裂缝形态。对比微地震监测结果发现，水力裂缝缝长在微地震的75.09%～99.63%，水力裂缝缝宽在微地震的78.79%～98.84%，模拟结果与实际监测具有较好的一致性。此方法可用于压裂前裂缝形态模拟，根据模拟结果制定压裂方案，提高压裂效率。

4. 结　论

1）综合考虑CO₂对岩体破裂压力、地应力的影响以及CO₂物性参数的变化，基于节点连接方法的CO₂增能压裂裂缝扩展数学模型可实现CO₂增能压裂复杂裂缝网络形态的模拟。

2）前置CO₂比例、应力差和渗透率对分支缝密度的影响较大，在高应力差储层增加缝网密度时，可适当增加前置CO₂比例。

3）实际区块模拟结果与微地震监测结果吻合度较高，具有一定的可靠性，基于节点连接方法的CO₂增能压裂裂缝扩展数学模型具有一定的现场应用潜力，可以为压裂方案的制定提供理论指导。

图 1 半圆弯曲试样及加载示意图

Figure 1. Semi-circular bending sample and loading

下载: 全尺寸图片幻灯片

图 2 不同围压下的层理页岩破坏试验结果

Figure 2. Failure test results of bedding shale at different confining pressures

下载: 全尺寸图片幻灯片

图 3 不同围压下的层理页岩破坏模式

Figure 3. Failure modes of bedding shale at different confining pressures

下载: 全尺寸图片幻灯片

图 4 层理页岩数值模型构建

Figure 4. Numerical model construction of bedding shale

下载: 全尺寸图片幻灯片

图 5 应力−应变曲线标定

Figure 5. Calibration of stress–strain curve

下载: 全尺寸图片幻灯片

图 6 试样失效模式对比

Figure 6. Failure mode comparison of samples

下载: 全尺寸图片幻灯片

图 7 半圆板三点弯曲数值模型

Figure 7. Three-point bending numerical models of semi-circular shale plate

下载: 全尺寸图片幻灯片

图 8 半圆弯曲试验和数值模拟获得的载荷−位移关系对比

Figure 8. Comparison of load–displacement relationships obtained by semi-circular bending experiment and numerical simulation

下载: 全尺寸图片幻灯片

图 9 不同围压下的页岩载荷−位移曲线

Figure 9. Load–displacement curves of shale at different confining pressures

下载: 全尺寸图片幻灯片

图 10 层理面密度0.80条/mm时的层理面角度−断裂韧性关系

Figure 10. Relationship between bedding plane angle and fracture toughness at bedding plane density of 0.8 fractures/mm

下载: 全尺寸图片幻灯片

图 11 不同层理面角度下SCB试样断裂模式

Figure 11. Fracture modes of SCB samples at different bedding plane angles

下载: 全尺寸图片幻灯片

图 12 层理面角度45°时的层理面密度−断裂韧性关系

Figure 12. Relationship between bedding plane density and fracture toughness at bedding plane angle of 45°

下载: 全尺寸图片幻灯片

图 13 不同层理面密度下的SCB试样断裂结果

Figure 13. Fracture results of SCB samples at different bedding plane densities

下载: 全尺寸图片幻灯片

图 14 权重系数a_σ和b_σ随围压的变化

Figure 14. Variations in the weight coefficients a_σ and b_σ with confining pressures

下载: 全尺寸图片幻灯片

图 15 不同围压下层理面性质对页岩断裂韧性影响的评价图版

Figure 15. Evaluation chart for influence of bedding plane properties on shale fracture toughness under different confining pressures

下载: 全尺寸图片幻灯片

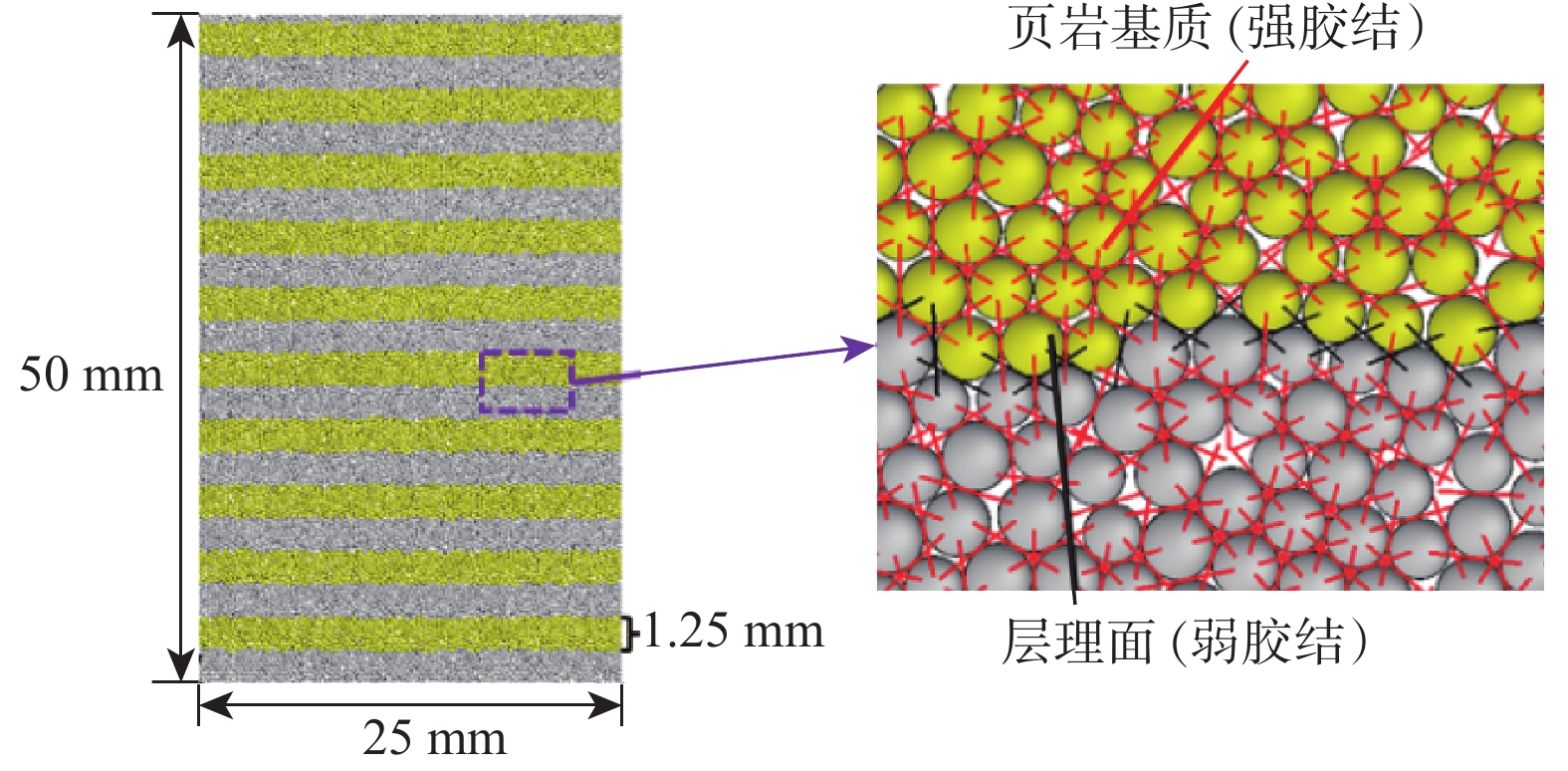
表 1 数值模型细观胶结参数取值

Table 1 Meso-cementation parameters of numerical model

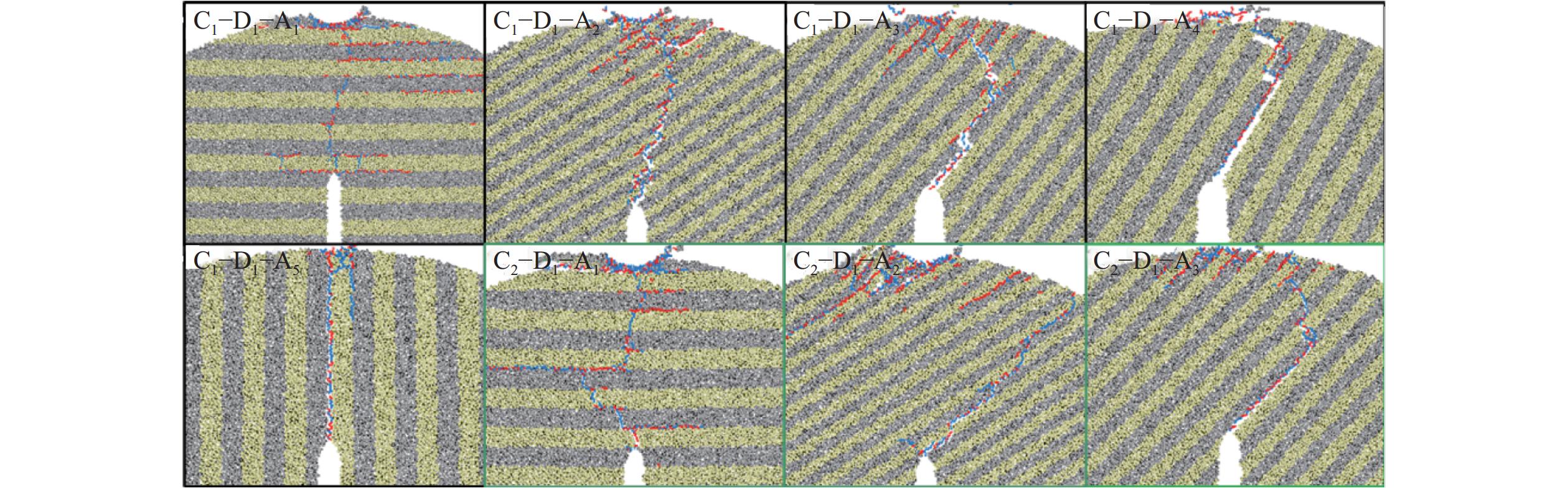
页岩	颗粒密度/ （kg·m⁻³）	颗粒有效模量/GPa	胶结有效模量/GPa	胶结刚度比	胶结拉伸强度/MPa	胶结内聚力/MPa	胶结摩擦角/（°）
基质	2 640	5.0	19.20	1.35	117.6	70.4	25
层理面	2 640	5.0	3.84	1.35	23.5	14.1	14

下载: 导出CSV

表 2 页岩数值模型的断裂韧性计算结果

Table 2 Fracture toughness calculation results of numerical model for shale

试样编号	F_max/kN	${K}'$	试样编号	F_max/kN	${K}'$
C₁−D₁−A₁	257.80	0.326	C₂−D₁−A₁	194.49	0.180
C₁−D₂−A₁	192.39	0.175	C₂−D₂−A₁	205.05	0.204
C₁−D₃−A₁	167.62	0.118	C₂−D₃−A₁	248.98	0.305
C₁−D₄−A₁	214.57	0.226	C₂−D₄−A₁	241.07	0.287
C₁−D₁−A₂	186.42	0.161	C₂−D₁−A₂	174.28	0.133
C₁−D₂−A₂	147.85	0.072	C₂−D₂−A₂	194.47	0.180
C₁−D₃−A₂	144.99	0.065	C₂−D₃−A₂	186.92	0.162
C₁−D₄−A₂	169.39	0.122	C₂−D₄−A₂	176.83	0.139

下载: 导出CSV

参考文献(19)

[1]	MAHANTA B, TRIPATHY A, VISHAL V, et al. Effects of strain rate on fracture toughness and energy release rate of gas shales[J]. Engineering Geology, 2017, 218: 39–49. doi: 10.1016/j.enggeo.2016.12.008
[2]	ATKINSON C, SMELSER R E, SANCHEZ J. Combined mode fracture via the cracked Brazilian disk test[J]. International Journal of Fracture, 1982, 18(4): 279–291.
[3]	吕有厂. 层理性页岩断裂韧性的加载速率效应试验研究[J]. 岩石力学与工程学报,2018,37(6):1359–1370. LYU Youchang. Effect of bedding plane direction on fracture toughness of shale under different loading rates[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1359–1370.
[4]	陈勉,金衍,袁长友. 围压条件下岩石断裂韧性的实验研究[J]. 力学与实践,2001,23(4):32–35. doi: 10.3969/j.issn.1000-0879.2001.04.010 CHEN Mian, JIN Yan, YUAN Changyou. Study on the experiment for fracture toughness under confining pressure[J]. Mechanics in Engineering, 2001, 23(4): 32–35. doi: 10.3969/j.issn.1000-0879.2001.04.010
[5]	董京楠,金衍,陈勉,等. 页岩Ⅰ型断裂韧性测试及跨尺度裂缝表征研究[J]. 地下空间与工程学报,2019,15(增刊1):205–210. DONG Jingnan, JIN Yan, CHEN Mian, et al. Study on shale fracture toughness and micro-characterization of mode Ⅰ crack using DCB specimen and SEM method[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(supplement 1): 205–210.
[6]	余海棠,丁乙,刘艳梅,等. 考虑水化损伤作用的页岩动态自吸模型[J]. 石油钻探技术,2023,51(5):139–148. doi: 10.11911/syztjs.2023054 YU Haitang, DING Yi, LIU Yanmei, et al. A dynamical spontaneous imbibition model for shale considering hydration damage[J]. Petroleum Drilling Techniques, 2023, 51(5): 139–148. doi: 10.11911/syztjs.2023054
[7]	金衍,薄克浩,张亚洲,等. 深层硬脆性泥页岩井壁稳定力学化学耦合研究进展与思考[J]. 石油钻探技术,2023,51(4):159–169. doi: 10.11911/syztjs.2023024 JIN Yan, BO Kehao, ZHANG Yazhou, et al. Advancements and considerations of chemo-mechanical coupling for wellbore stability in deep hard brittle shale[J]. Petroleum Drilling Techniques, 2023, 51(4): 159–169. doi: 10.11911/syztjs.2023024
[8]	谭鹏,陈朝伟,赵庆,等. 页岩气多簇压裂断层活化机理与控制方法[J]. 石油钻探技术,2024,52(6):107–116. doi: 10.11911/syztjs.2024120 TAN Peng, CHEN Zhaowei, ZHAO Qing, et al. Mechanism and control method of fault activation by multi-cluster fracturing of shale gas[J]. Petroleum Drilling Techniques, 2024, 52(6): 107–116. doi: 10.11911/syztjs.2024120
[9]	刘彧轩,杨兴贵,郭建春. 纵向无限级多薄层储层裂缝穿层扩展规律[J]. 断块油气田,2024,31(6):1076–1082. LIU Yuxuan, YANG Xinggui, GUO Jianchun. Fracture through-layer propagation law in longitudinal infinite multiple thin layer reservoirs[J]. Fault-Block Oil & Gas Field, 2024, 31(6): 1076–1082.
[10]	田建超,张艺,李凝,等. 页岩油水力压裂裂缝特征场地级数值模拟优化方法[J]. 石油钻采工艺,2024,46(3):326–335. TIAN Jianchao, ZHANG Yi, LI Ning, et al. Numerical simulation optimization method for site-level hydraulic fracturing fracture characteristics in shale oil[J]. Oil Drilling & Production Technology, 2024, 46(3): 326–335.
[11]	赵彦昕,许文俊,王雷,等. 陆相页岩储层水力裂缝穿层扩展规律[J]. 石油钻采工艺,2023,45(1):76–84. ZHAO Yanxin, XU Wenjun, WANG Lei, et al. Through-layer propagation laws of hydraulic fractures in continental shale reservoirs[J]. Oil Drilling & Production Technology, 2023, 45(1): 76–84.
[12]	熊健,吴俊,刘向君,等. 陆相页岩储层地质力学特性及对压裂效果的影响[J]. 西南石油大学学报(自然科学版),2023,45(5):69–80. XIONG Jian, WU Jun, LIU Xiangjun, et al. The geomechanical characteristics of the continental shale reservoirs and their influence on the fracturing effect[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2023, 45(5): 69–80.
[13]	张景轩,范晓,陈波,等. 硬脆性页岩断裂韧性二维数值模拟研究[J]. 复杂油气藏,2019,12(1):73–80. ZHANG Jingxuan, FAN Xiao, CHEN Bo, et al. Two-dimensional numerical simulation of fracture toughness of hard brittle shale[J]. Complex Hydrocarbon Reservoirs, 2019, 12(1): 73–80.
[14]	XU Yuan, DAI Feng, ZHAO Tao, et al. Fracture toughness determination of cracked chevron notched Brazilian disc rock specimen via Griffith energy criterion incorporating realistic fracture profiles[J]. Rock Mechanics and Rock Engineering, 2016, 49(8): 3083–3093. doi: 10.1007/s00603-016-0978-0
[15]	YIN Tubing, ZHANG Shuaishua, LI Xibing, et al. A numerical estimate method of dynamic fracture initiation toughness of rock under high temperature[J]. Engineering Fracture Mechanics, 2018, 204: 87–102. doi: 10.1016/j.engfracmech.2018.09.034
[16]	KURUPPU M D, OBARA Y, AYATOLLAHI M R, et al. ISRM-suggested method for determining the mode I static fracture toughness using semi-circular bend specimen[J]. Rock Mechanics and Rock Engineering, 2014, 47(1): 267–274. doi: 10.1007/s00603-013-0422-7
[17]	张昊天,周文,曹茜,等. 基于应力—应变模型的脆塑性测井评价[J]. 测井技术,2018,42(3):331–337. ZHANG Haotian, ZHOU Wen, CAO Qian, et al. Log evaluation method of the brittle-plastic parameters based on stress-strain model[J]. Well Logging Technology, 2018, 42(3): 331–337.
[18]	CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47–65.
[19]	李庆辉,陈勉,金衍,等. 页岩气储层岩石力学特性及脆性评价[J]. 石油钻探技术,2012,40(4):17–22. doi: 10.3969/j.issn.1001-0890.2012.04.004 LI Qinghui, CHEN Mian, JIN Yan, et al. Rock mechanical properties and brittleness evaluation of shale gas reservoir[J]. Petroleum Drilling Techniques, 2012, 40(4): 17–22. doi: 10.3969/j.issn.1001-0890.2012.04.004

施引文献(9)

期刊类型引用(9)

1.	徐智颢，杜博，李东东. 裂缝内CO_2压裂液相态分布特征的数值模拟研究. 中国资源综合利用. 2024(04): 41-43 . 百度学术
2.	孟宪波. 页岩油藏水平井分段多簇压裂全井段裂缝扩展数值模拟——以济阳坳陷沙河街组为例. 断块油气田. 2024(03): 459-466 . 百度学术
3.	李阳，祝仰文，李宗阳，蒋廷学，薛兆杰，沈子齐，肖朴夫，于洪敏，程紫燕，赵清民，张庆福. 济阳坳陷页岩油注二氧化碳开发技术. 石油勘探与开发. 2024(04): 855-864 . 百度学术
4.	孙丙向，成海，毕研涛. 石油工程“四提”技术进展与攻关方向. 石油科技论坛. 2024(03): 85-94 . 百度学术
5.	李阳，曹小朋，赵清民，刘祖鹏，薛兆杰，蒋龙. 济阳坳陷陆相断陷盆地页岩油开发的几点思考. 石油钻探技术. 2024(04): 1-7 . 本站查看
6.	吴壮坤，张宏录，池宇璇. 苏北页岩油二氧化碳强压质换技术. 石油钻探技术. 2024(04): 87-93 . 本站查看
7.	LI Yang，ZHU Yangwen，LI Zongyang，JIANG Tingxue，XUE Zhaojie，SHEN Ziqi，XIAO Pufu，YU Hongmin，CHENG Ziyan，ZHAO Qingmin，ZHANG Qingfu. Shale oil recovery by CO_2 injection in Jiyang Depression, Bohai Bay Basin, East China. Petroleum Exploration and Development. 2024(04): 981-992 . 必应学术
8.	余前港，荣双，毛国扬，崔连文，彭根博，向传刚，王旭. 阳春沟区块页岩气超临界CO_2增能压裂研究与应用. 石油与天然气化工. 2024(05): 77-83 . 百度学术
9.	李阳，赵清民，杨勇，张峰，曹功泽，张潦源，杨峰，鲁明晶. 胜利油田陆相页岩油前置CO_2压裂技术研究与实践. 断块油气田. 2024(06): 945-954 . 百度学术

其他类型引用(0)

资源附件(0)

图(15) / 表(2)

计量

文章访问数: 80
HTML全文浏览量: 16
PDF下载量: 34
被引次数: 9

1. CO2增能压裂裂缝扩展模拟模型
1.1 CO2岩石压裂起裂压力与应力变化表征
1.2 CO2物性参数变化表征
1.3 基于NCM的CO2增能压裂裂缝扩展数学模型
1.3.1 前置CO2水力压裂力学机制
1.3.2 前置CO2压裂模拟流程
2. 前置CO2增能压裂裂缝扩展模拟
2.1 前置CO2比例对缝网形态的影响
2.2 水平应力差对裂缝形态的影响
2.3 储层渗透率对裂缝形态的影响
3. 实例分析
4. 结　论

1. CO₂增能压裂裂缝扩展模拟模型
1.1 CO₂岩石压裂起裂压力与应力变化表征
1.2 CO₂物性参数变化表征
1.3 基于NCM的CO₂增能压裂裂缝扩展数学模型
1.3.1 前置CO₂水力压裂力学机制
1.3.2 前置CO₂压裂模拟流程
2. 前置CO₂增能压裂裂缝扩展模拟
2.1 前置CO₂比例对缝网形态的影响
2.2 水平应力差对裂缝形态的影响
2.3 储层渗透率对裂缝形态的影响
3. 实例分析
4. 结　论

参考文献(19)

施引文献(9)

资源附件(0)

超深纹层页岩断裂韧性演化规律研究

作者简介: 燕鸣飞（1997—），男，山西临汾人，2020年毕业于中国石油大学（北京）石油工程专业，在读博士研究生，主要从事岩石力学与井壁稳定方面的研究工作。E-mail：15611788113@163.com

通讯作者: 金衍，jiny@cup.edu.cn

计量

出版历程

Study on Evolution Law of Fracture Toughness of Ultra-Deep Laminated Shale

1. CO2增能压裂裂缝扩展模拟模型

1.1 CO2岩石压裂起裂压力与应力变化表征

1.2 CO2物性参数变化表征

1.3 基于NCM的CO2增能压裂裂缝扩展数学模型

1.3.1 前置CO2水力压裂力学机制

1.3.2 前置CO2压裂模拟流程

2. 前置CO2增能压裂裂缝扩展模拟

2.1 前置CO2比例对缝网形态的影响

2.2 水平应力差对裂缝形态的影响

2.3 储层渗透率对裂缝形态的影响

3. 实例分析

4. 结 论

期刊类型引用(9)

其他类型引用(0)

计量

出版历程

目录

1. CO2增能压裂裂缝扩展模拟模型

1.1 CO2岩石压裂起裂压力与应力变化表征

1.2 CO2物性参数变化表征

1.3 基于NCM的CO2增能压裂裂缝扩展数学模型

1.3.1 前置CO2水力压裂力学机制

1.3.2 前置CO2压裂模拟流程

2. 前置CO2增能压裂裂缝扩展模拟

2.1 前置CO2比例对缝网形态的影响

2.2 水平应力差对裂缝形态的影响

2.3 储层渗透率对裂缝形态的影响

3. 实例分析

4. 结 论

作者简介:
燕鸣飞（1997—），男，山西临汾人，2020年毕业于中国石油大学（北京）石油工程专业，在读博士研究生，主要从事岩石力学与井壁稳定方面的研究工作。E-mail：15611788113@163.com

通讯作者:
金衍，jiny@cup.edu.cn

1. CO₂增能压裂裂缝扩展模拟模型

1.1 CO₂岩石压裂起裂压力与应力变化表征

1.2 CO₂物性参数变化表征

1.3 基于NCM的CO₂增能压裂裂缝扩展数学模型

1.3.1 前置CO₂水力压裂力学机制

1.3.2 前置CO₂压裂模拟流程

2. 前置CO₂增能压裂裂缝扩展模拟

2.1 前置CO₂比例对缝网形态的影响

4. 结　论

1. CO₂增能压裂裂缝扩展模拟模型

1.1 CO₂岩石压裂起裂压力与应力变化表征

1.2 CO₂物性参数变化表征

1.3 基于NCM的CO₂增能压裂裂缝扩展数学模型

1.3.1 前置CO₂水力压裂力学机制

1.3.2 前置CO₂压裂模拟流程

2. 前置CO₂增能压裂裂缝扩展模拟

2.1 前置CO₂比例对缝网形态的影响

4. 结　论