基于对应分析的丽水–椒江凹陷潜山岩性识别方法

王雷; 韩学彪; 曹英权; 景社; 袁胜斌; 许怀智

doi:10.11911/syztjs.2024019

基于对应分析的丽水–椒江凹陷潜山岩性识别方法

1.
中海石油（中国）有限公司上海分公司, 上海 200335
2.
中法渤海地质服务有限公司, 天津 300452

基金项目: 中国海洋石油有限公司重大科技项目“海上深层/超深层油气勘探技术”（编号：KJGG2022-0405）部分研究内容。

详细信息

作者简介:
王雷（1976—），男，山东郓城人，2002年毕业于石油大学（华东）石油与天然气地质勘察专业，2005年获中国科学院兰州地质研究所矿物学、岩石学、矿床学专业硕士学位，高级工程师，主要从事现场地质作业及相关技术管理工作。E-mail：wanglei5@cnooc.com.cn

中图分类号: TE122
计量
- 文章访问数: 87
- HTML全文浏览量: 6
- PDF下载量: 34
出版历程
- 收稿日期: 2023-05-11
- 修回日期: 2023-12-08
- 网络出版日期: 2024-01-16
- 刊出日期: 2024-01-24

A Lithology Identification Method for Buried Hills in the Lishui-Jiaojiang Sag Based on Correspondence Analysis

1.
Shanghai Branch of CNOOC China Limited, Shanghai, 200335, China
2.
ChinaFrance Bohai Geoservices Co., Ltd., Tianjin, 300452, China

摘要

摘要:
随着丽水–椒江凹陷油气勘探扩展至潜山油藏，钻井揭示花岗岩、片麻岩、灰岩等岩性地层；加之应用了钻井新工艺，录井岩屑细小、混杂，现场准确识别岩性难度较大。为了解决此问题，基于XRD衍射和XRF元素录井资料，利用ReliefF算法筛选了对潜山及上覆地层敏感的8种元素和4种矿物，将筛选出的元素、矿物作为原始数据集的特征参数进行对应分析，构建了花岗岩、片麻岩、灰岩等岩石岩性的H₁与H₂函数，并建立了复杂岩性的识别图版。其中，花岗岩的H₁和H₂分别为–3.0～1.0和1.0～3.0，片麻岩的H₁和H₂分别为–4.0～0和–2.5～1.0，灰岩的H₁和H₂分别为0.5～2.5和–9.0～–3.0，砂砾岩的H₁和H₂分别为2.5～10.0和–1.0～2.5，泥岩的H₁和H₂分别为–1.0～3.5和–1.0～0.5。丽水–椒江凹陷潜山油气区6口井应用了基于对应分析的岩性识别方法，识别复杂岩性的准确率达90.7％，可为钻井施工安全及潜山储层综合评价提供技术支持。
- 对应分析 /
- 岩性识别 /
- XRD衍射录井 /
- XRF元素录井 /
- 丽水–椒江凹陷
Abstract:
As oil and gas exploration in the Lishui-Jiaojiang Sag moves towards buried hills, drilling has encountered many lithology formations such as granite, gneiss, and limestone. In addition, with the application of new drilling technology, the cuttings for logging are fine and usually mixed together, and it is difficult to identify the lithology accurately on the well site. In order to solve this problem, based on X-ray diffraction (XRD) and X-ray fluorescence (XRF) element logging data, firstly, the ReliefF algorithm was used to identify eight elements and four minerals sensitive to buried hills and overlying strata, and then the selected elements and minerals were used as the characteristic parameters of the original data set for corresponding analysis. The H₁and H₂ functions of granite, gneiss, limestone, and other complex lithologies were established, and the complex lithology identification chart was drawn. Specifically, the H₁and H₂ of granite were −3.0～1.0 and 1.0～3.0, and those of gneiss were −4.0～0 and −2.5～1.0. The H₁and H₂ of limestone were 0.5～2.5 and −9.0～−3.0, and those of sandstone were 2.5～10.0 and −1.0～2.5. In addition, the H₁and H₂ of mudstone were −1.0～3.5 and −1.0～0.5. The lithology identification method based on corresponding analysis was applied to six wells in the oil and gas area of the Lishui-Jiaojiang Sag, and the identification accuracy of complex lithology reached 90.7%, which can provide technical support for drilling operation safety and comprehensive evaluation of buried hill reservoirs.
- correspondence analysis /
- lithology identification /
- XRD logging /
- XRF element logging /
- the Lishui-Jiaojiang Sag

HTML全文

丽水–椒江凹陷是东海盆地油气勘探的重点地区，位于东海盆地西南部^[1–2]，是在前中生界基底之上发育起来的中新生代沉积凹陷，面积约1.7×10⁴ km²^[3–4]。随着该地区油气勘探的不断深入，在灵峰潜山构造带L1井潜山段见到较好油气显示，开启了丽水–椒江凹陷潜山油气勘探的序幕，潜山逐渐成为该地区未来储量增长的重要领域^[5–11]。但是，在潜山油气钻探过程中，在潜山界面上下钻遇了花岗岩、片麻岩、灰岩、泥岩和砂砾岩等岩性地层。对于勘探作业，及时准确地识别地层岩性并卡准潜山界面是确保钻井安全、提高油气勘探效率的重要保障。但随着钻井技术不断进步，特别是PDC 钻头^[12–13]、涡轮钻具组合^[14]、气体钻井技术等的推广应用，录井采集到的岩屑变得细小、混杂，现场识别岩性往往依赖地质人员的经验，在周边钻井资料较少的情况下，岩性识别手段有限，给潜山油气高效勘探带来了挑战。

为应对潜山复杂岩性的识别问题，国内各大油田相继引入XRD衍射和XRD元素录井技术，通过开展基于机器学习的岩性智能识别及预测研究，采用决策树、随机森林、梯度提升树和贝叶斯算法等方法识别地层岩性^[15–16]，取得了一定进展，但计算过程复杂，且受限于样本点数量，识别精度仍未能满足现场需要。针对丽水–椒江凹陷潜山岩性识别难的问题，笔者以研究区潜山已钻井XRD衍射和XRD元素录井资料为基础，利用ReliefF算法筛选出敏感元素和敏感矿物，将其作为原始数据集的特征参数进行了对应分析，在确定2个主因子判别函数的基础上，建立了研究区复杂岩性识别图版，消除了各岩石岩性之间的重叠区域，实现了在井场快速、准确识别潜山地层的岩性。

1. 对应分析法原理及岩性识别图版

1.1 对应分析法原理

对应分析（correspondence analysis，CA）^[17–19]也称关联分析或R-Q型因子分析，是在R型因子和Q型因子分析的基础上发展起来的一种多元统计分析技术，广泛用于分析属性–变量二维数据矩阵中行因素和列因素间的关系。此前，无论是R型因子还是Q型因子，由于相似性度量和数据矩阵变换方式的不同，很难用于反映变量与样品之间的关系；对应分析将R型数据与Q型数据相对应，从而可以将其同时反映到相同坐标轴的图形上进行分析，在一个二维图上同时表示二者之间的各种状态，可以直观地表示其原有数据结构，从而更好地表示样品属性与变量属性之间的关系。计算步骤如下^[15]：

设有n个样品，每个样品测了m个指标，原始数据矩阵为：

${\boldsymbol{X}}= \left[\begin{array}{cccc}{{x}}_{11}& {{x}}_{12}& \cdots & {{x}}_{1{n}}\\ {{x}}_{21}& {{x}}_{22}& \cdots & {{x}}_{2{n}}\\ \vdots& \vdots& \cdots & \vdots\\ {{x}}_{{m}1}& {{x}}_{{m}2}& \cdots & {{x}}_{{m}{n}}\end{array}\right]$

(1)

式中： ${ {x}}_{ {r} {j}}$ （ ${r}= {1,2},\cdots {m}; {j}= {1,2},\cdots {n}$ ）表示第j个样品的第r个观测值， ${ {x}}_{ {r} {j}}\geqslant 0$ 。

1）求Z矩阵。把原始矩阵X变换为Z矩阵：

${{z}}_{{r}{j}}=\frac{{{x}}_{{r}{j}}-\dfrac{{{x}}_{{r}.}{{x}}_{.{j}}}{{T}}}{\sqrt{{{x}}_{{r}.}{{x}}_{.{j}}}}\quad({r}={1,2}\cdots ,{m};{j}={1,2},\cdots {n}) .$

(2)

$\, 其中\qquad\qquad {{x}}_{{r}.}={\sum} _{{j}=1}^{{n}}{{x}}_{{r}{j}} \quad({r}={1,2},\cdots ,{m}) \quad$

(3)

$\quad\;\; {{x}}_{.{j}}={\sum} _{{r}=1}^{{m}}{{x}}_{{r}{j}} \quad ({j}={1,2},\cdots ,{n})$

(4)

$T={\sum }_{{r}=1}^{{m}}{\sum} _{{j}=1}^{{n}}{{x}}_{{r}{j}}$

(5)

2）R型因子求解。计算协方差矩阵 ${{{\boldsymbol{Z}}}{{\boldsymbol{Z}}}}'$ 的特征值 λ₁， λ₂， …，λ_m（ ${{\lambda }}_{1}\geqslant{{\lambda }}_{2}\geqslant\cdots \geqslant{{\lambda }}_{{m}}$ ），并计算出相应的单位特征向量 ${{\boldsymbol{U}}}=\left[{{u}}_{1},{{u}}_{2},\cdots ,{{u}}_{{m}}\right]$ ，据累计贡献率是否大于80%，确定主因子k（一般取k=2或3），得到因子载荷矩阵，以因子载荷为坐标，在两两因子轴平面上做指标点图。

${\boldsymbol{F}}=\left[\begin{array}{cccc}{{u}}_{11}\sqrt{{{\lambda }}_{1}}& {{u}}_{12}\sqrt{{{\lambda }}_{2}}& \cdots & {{u}}_{1{k}}\sqrt{{{\lambda }}_{{k }}}\\ {{u}}_{21}\sqrt{{{\lambda }}_{1}}& {{u}}_{22}\sqrt{{{\lambda }}_{2}}& \cdots & {{u}}_{2{k}}\sqrt{{{\lambda }}_{{k }}}\\ \vdots& \vdots& \cdots & \vdots\\ {{u}}_{{m}1}\sqrt{{{\lambda }}_{1}}& {{u}}_{{m}2}\sqrt{{{\lambda }}_{2}}& \cdots & {{u}}_{{m}{k}}\sqrt{{{\lambda }}_{{k }}}\end{array}\right]$

(6)

3）Q型因子求解。计算R型前 k 个特征值对应于矩阵 ${{\boldsymbol{B}}}={{{\boldsymbol{Z}}}}'{{\boldsymbol{Z}}}$ 的单位特征向量：

${{{\boldsymbol{q}}}}_{{i}}=\frac{1}{\sqrt{{{\lambda }}_{{i}}}}{\boldsymbol{Z}}'{{u}}_{{i}}\quad ( {i}={1,2},\cdots ,{k } )$

(7)

${{{\boldsymbol{V}}}}_{{i}}={{q}}_{{i}}\sqrt{{{\lambda }}_{{i}}}={\boldsymbol{Z}}'{{u}}_{{i}} \quad( {i}={1,2},\cdots ,{k } )$

(8)

利用式（8），求得Q型因子载荷矩阵：

${\boldsymbol{G}} = \left[\begin{array}{cccc}{{v}}_{11}\sqrt{{{\lambda }}_{1}}& {{v}}_{12}\sqrt{{{\lambda }}_{2}}& \cdots & {{v}}_{1{k}}\sqrt{{{\lambda }}_{{k }}}\\ {{v}}_{21}\sqrt{{{\lambda }}_{1}}& {{v}}_{22}\sqrt{{{\lambda }}_{2}}& \cdots & {{v}}_{2{k}}\sqrt{{{\lambda }}_{{k }}}\\ \vdots& \vdots& \cdots & \vdots\\ {{v}}_{{n}1}\sqrt{{{\lambda }}_{1}}& {{v}}_{{n}2}\sqrt{{{\lambda }}_{2}}& \cdots & {{v}}_{{n}{k}}\sqrt{{{\lambda }}_{{k }}}\end{array}\right]$

(9)

最后，在 R 型因子分析的因子平面上，以 Q 型因子载荷为坐标把样品点表示出来，并对指标与样品进行地质解释。

1.2 复杂岩性识别图版

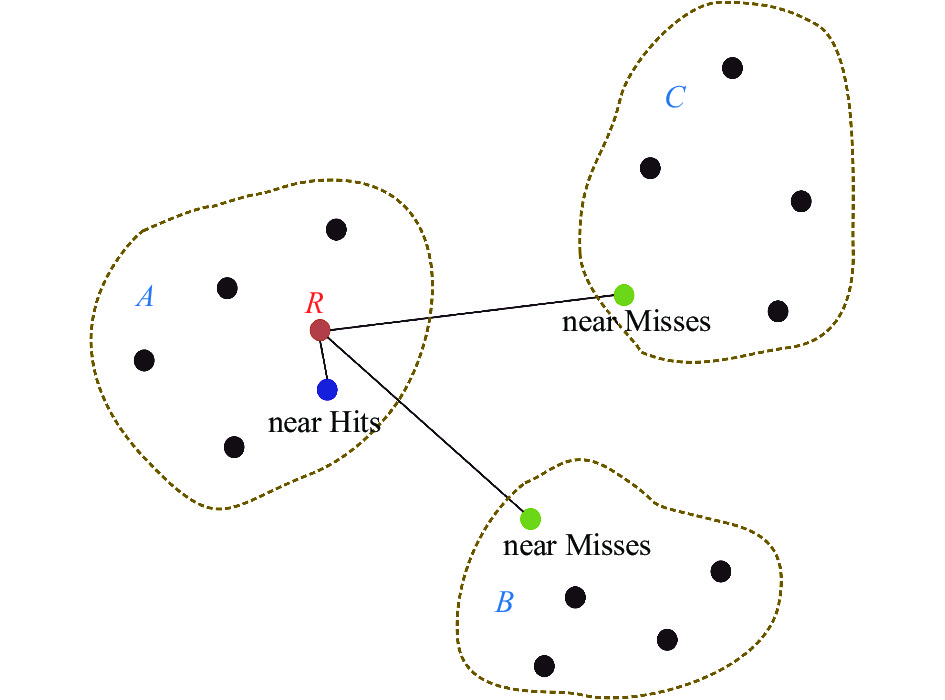
基于XRD衍射录井资料和XRF元素录井资料^[20]，利用ReliefF算法对丽水–椒江凹陷潜山与上覆地层岩石类型的矿物及元素进行了统计。该算法的核心思想是每一次从训练集中随机取出一个样本R，然后在同类别样本集中选取和R相邻的w个近邻样本（near Hits），从不同类别样本集合中也同样找出w个近邻样本（near Misses）（见图1），通过多次计算和迭代，得到各个特征的最终权重。权重越大，表示该特征对样本的区分能力越强^[17–19]。

图 1 ReliefF算法近邻样本选择示意

Figure 1. Neighbor sample selection for the ReliefF algorithm

下载: 全尺寸图片幻灯片

丽水–椒江凹陷潜山及上覆地层XRF元素录井中共检测出11种元素，通过权重分析优选出8种占比高的敏感元素，分别为硅、钙、铁、镁、铝、钠、硫、钾，经归一化处理后，其权重分别为23.58%，21.19%，16.07%，11.29%，8.53%，7.63%，6.35%和5.36%。XRD衍射录井共检测到5种矿物，通过权重分析，优选出4种敏感矿物，分别为长石、石英、方解石、黏土，经过归一化处理后，其权重分别为28.94%，26.81%，26.75%和17.50%。

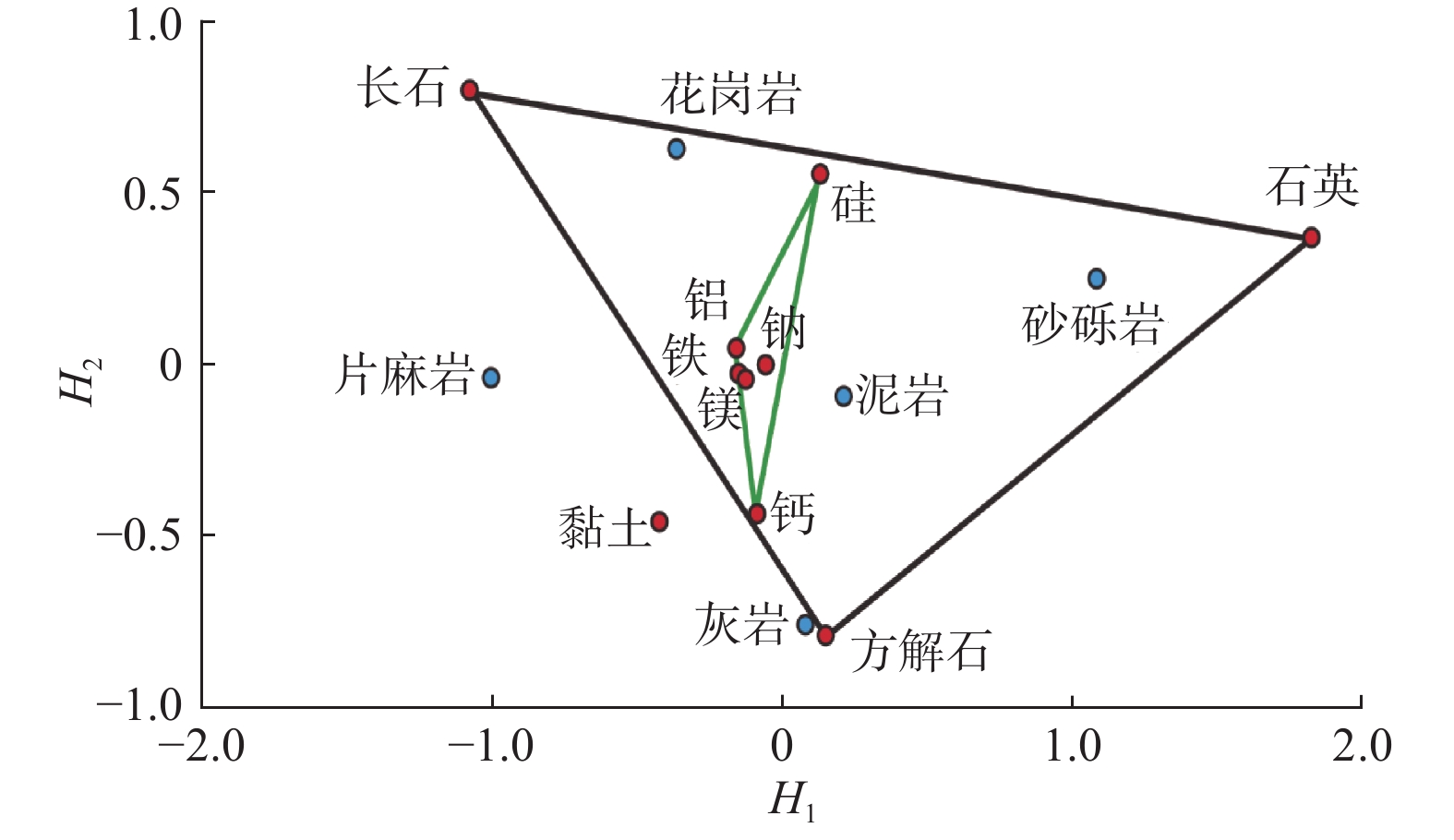
将ReliefF算法筛选出的敏感元素及敏感矿物作为原始数据集的特征参数进行对应分析，确定出2个主因子，主因子H₁方差占数据总体方差的78.2%，主因子H₂方差占数据总体方差的15.8%，二者累计方差贡献为94.0%，可以代表整个原始数据的信息。计算10个地质变量在H₁和H₂主因子载荷轴上的得分（见表1），可以看出，在H₁和H₂轴上得分绝对值较高的元素及矿物分别为石英、长石、方解石、硅、黏土矿物、钙和铝等。从岩石岩性–成分对应分析因子载荷得分（见图2）也可以看出以下3个层次的关系：

表 1 对应分析因子载荷

Table 1. Factor load for correspondence analysis

元素/矿物	H₁载荷得分	H₂载荷得分
铝	–0.155	0.049
钙	–0.081	–0.436
铁	–0.149	–0.028
镁	–0.125	–0.04
硅	0.126	0.525
钠	–0.061	–0.005
石英	1.808	0.373
长石	–1.076	0.802
方解石	0.139	–0.784
黏土	–0.425	–0.456

下载: 导出CSV

| 显示表格

图 2 岩石岩性–成分对应分析载荷

Figure 2. Load for correspondence analysis of rock type and cuttings composition

下载: 全尺寸图片幻灯片

1）岩石成分间的关系。邻近的一些变量点表示这些变量紧密相关，即他们具有成因上的联系，指示某一特点的地质作用，如铝、铁、镁与钠元素之间紧密相关，钙与方解石之间紧密相关。

2）岩石岩性间的关系。邻近的样品具有相似的性质，属于同一类型，是相同地质作用的产物。如研究区灰岩和泥岩之间的距离较小，表明该区灰岩中含有泥质成分；片麻岩与花岗岩、泥岩之间的距离较近，表明片麻岩的原岩可能为花岗岩或泥岩。

3）岩石成分与岩性间的关系。同一岩性的岩石将为邻近的成分所表征，也就是说，同类样品点为其邻近变量点所指示地质作用下的产物。如灰岩为方解石和钙元素地质作用下的产物；泥岩为铝、铁、镁与钠元素作用下的产物。

石英、长石和方解石矿物分别位于近似等边三角形的3个端元，元素硅、铝、钙同样组成近似等边三角形的3个端元位于矿物组成三角形内部，表明矿物成分对岩石类型的划分效果优于元素，二者之间相辅相成、互为补充，共同起作用完成岩石岩性的识别。

通过以上岩石岩性与矿物成分、元素之间的对应分析，将对应分析因子载荷得分与各岩石岩性对应矿物、元素特征相结合，计算研究区判别函数H₁和H₂，以使岩石岩性之间的差别最大化，提高岩石岩性识别的准确性。

$\begin{split} {H}_{1}=&-0.155\omega \left(\mathrm{A}\mathrm{l}\right)-0.081\omega \left(\mathrm{C}\mathrm{a}\right)-0.149\omega \left(\mathrm{F}\mathrm{e}\right)-\\ &0.125\omega \left(\mathrm{M}\mathrm{g}\right)+0.126\omega \left(\mathrm{S}\mathrm{i}\right)-0.061\omega \left(\mathrm{N}\mathrm{a}\right)+\\ &1.808\omega \left(\mathrm{Q}\mathrm{t}\mathrm{z}\right)-1.076\omega \left(\mathrm{F}\mathrm{l}\mathrm{e}\mathrm{d}\right)+ 0.139\omega \left(\mathrm{C}\mathrm{a}\mathrm{l}\right)-\\ &0.425\omega \left(\mathrm{C}\mathrm{l}\mathrm{a}\mathrm{y}\right)\\[-1pt] \end{split}$

(10)

$\begin{split} {H}_{2}=&0.049\omega \left(\mathrm{A}\mathrm{l}\right)-0.436\omega \left(\mathrm{C}\mathrm{a}\right)-0.028\omega \left(\mathrm{F}\mathrm{e}\right)-\\ &0.04\omega \left(\mathrm{M}\mathrm{g}\right)+0.525\omega \left(\mathrm{S}\mathrm{i}\right)-0.005\omega \left(\mathrm{N}\mathrm{a}\right)+\\ &0.373\omega \left(\mathrm{Q}\mathrm{t}\mathrm{z}\right)+0.802\omega \left(\mathrm{F}\mathrm{l}\mathrm{e}\mathrm{d}\right)-0.784\omega \left(\mathrm{C}\mathrm{a}\mathrm{l}\right)-\\ &0.456\omega \left(\mathrm{C}\mathrm{l}\mathrm{a}\mathrm{y}\right)\\[-1pt] \end{split}$

(11)

式中：ω(Al)为铝元素质量分数；ω(Ca)为钙元素质量分数；ω(Fe)为铁元素质量分数；ω(Mg)为镁元素质量分数；ω(Si)为硅元素质量分数；ω(Na)为钠元素质量分数；ω(Qtz)为石英质量分数；ω(Fled)为长石质量分数；ω(Cal)为方解石质量分数；ω(Clay)为黏土质量分数。

根据计算结果，建立了判别函数图版，如图3所示。从图3可以看出，花岗岩的H₁和H₂分别为–3.0～1.0和1.0～3.0，片麻岩的H₁和H₂分别为–4.0～0和–2.5～1.0，灰岩的H₁和H₂分别为0.5～2.5和–9.0～–3.0，砂砾岩的H₁和H₂分别为2.5～10.0和–1.0～2.5，泥岩的H₁和H₂分别为–1.0～3.5和–1.0～0.5，消除了各岩石类型之间的重叠区域，提高了潜山界面上下岩性识别的准确性。

图 3 对应分析岩性识别图版

Figure 3. Lithology identification chart for correspondence analysis

下载: 全尺寸图片幻灯片

2. 应用实例

随着XRD衍射录井和XRF元素录井技术水平的不断进步，目前已经成为丽水–椒江凹陷潜山复杂岩性识别的关键技术手段，而基于对应分析的丽水–椒江凹陷潜山岩性识别方法在6口新钻探井中进行了应用，钻井后井壁取心及镜下薄片鉴定结果表明，该方法对于复杂岩性识别的准确率达90.7%，提高了复杂岩性的识别率，为东海潜山勘探提供了技术支持。下面以X3井为例，分析其应用情况及效果。

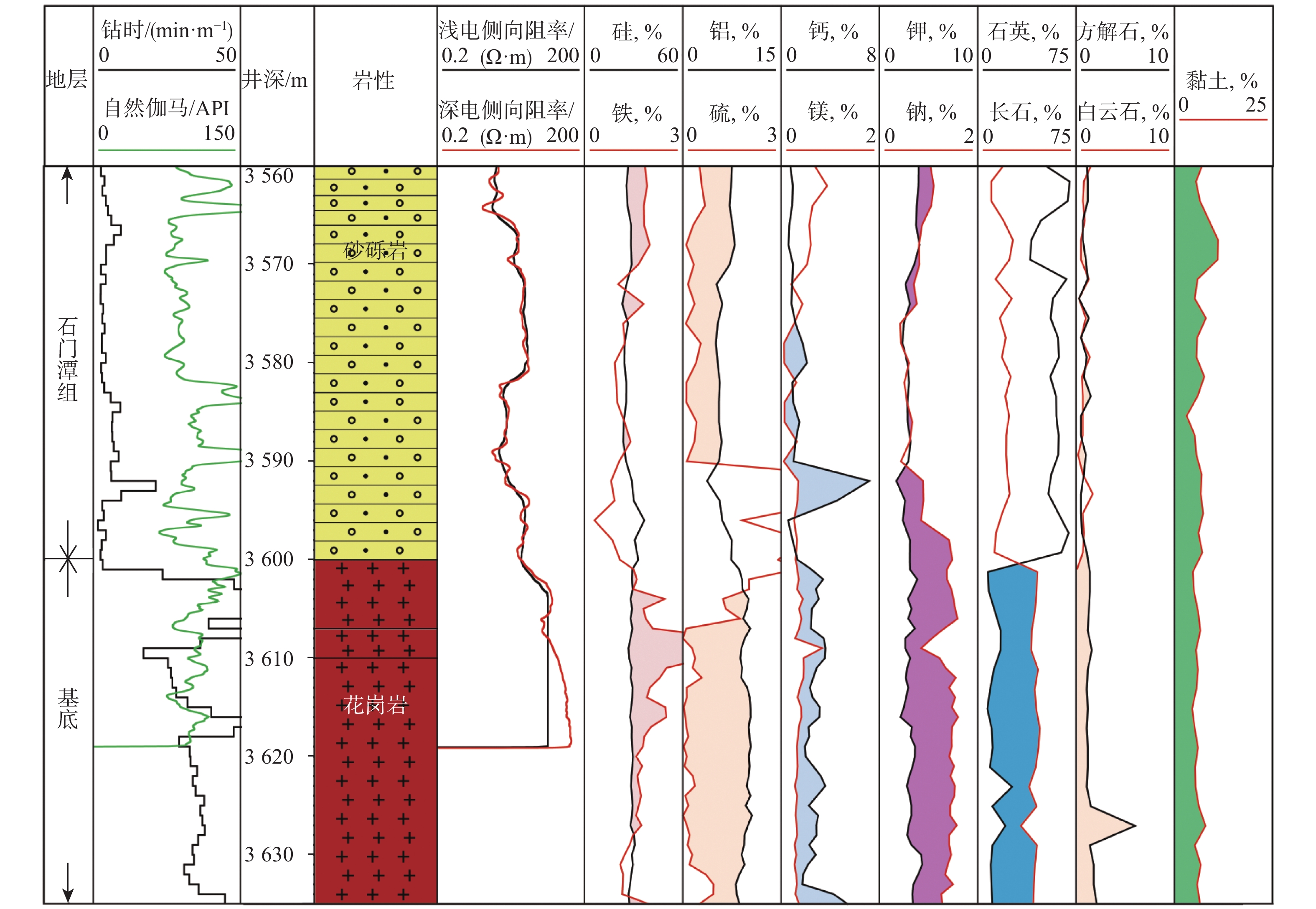
X3探井位于丽水–椒江凹陷仙桥构造带，钻前区域构造演化分析表明，其基底为断陷期形成的后成潜山，被上白垩统石门潭组覆盖。该井设计潜山顶井深3 855 m，实钻过程中钻至井深3 600 m时，对比上覆厚层砂砾岩，电阻率明显升高，但现场岩屑与上覆砂砾岩地层未见明显差异，无法判断岩性是否发生改变。为了解决该井段岩性识别难题，分析该井段的XRD衍射和XRF元素录井资料，发现井深3 600 m处上下地层元素及矿物成分出现突变（见图4），其中钙、镁、铁、钠元素含量递进式升高，硫元素含量降低，矿物成分长石含量增加，石英、黏土含量明显降低，元素、矿物均发生了变化，说明该井段岩性可能发生了改变。

图 4 X3井元素及矿物变化综合柱状图

Figure 4. Composite bar chart of changes in elements and minerals of Well X3

下载: 全尺寸图片幻灯片

利用对应分析法将XRD衍射与XRF元素录井数据进行标准化处理后代入式（10）、式（11），并进行岩石岩性识别图版的投点（见图3），3 580～3 600 m井段地层投点落入图版中砂砾岩区，判断岩性为砂砾岩；3 600～3 620 m井段地层投点落入图版中花岗岩区，判断岩性为花岗岩。后续的井壁取心和薄片鉴定结果进一步证实，3 580～3 600 m井段地层的岩性为砂砾岩、井深3 600 m以深地层的岩性为花岗岩，井深3 600 m为潜山与上覆砂砾岩的地层界面，该井较预测提前255 m进入潜山地层。该方法为钻井工程安全提供保障、为潜山储层的综合研究提供了技术支撑，同时验证了对应分析法在该地区复杂岩性识别中的适用性。

3. 结　论

1）利用ReliefF算法对丽水–椒江凹陷潜山与上覆地层岩石类型的矿物及元素进行统计，根据相关性赋予特征不同的权重，优选出丽水–椒江凹陷潜山及上覆地层敏感元素为硅、钙、铁、镁、铝、钠、硫和钾，敏感矿物为长石、石英、方解石及黏土矿物。

2）利用对应分析算法将筛选出的敏感元素及敏感矿物作为原始数据集的特征参数进行对应分析，将对应分析因子载荷得分与各岩石岩性对应矿物、元素特征相结合，计算出了研究区的判别函数H₁和H₂，最大化了岩石类型之间的差别，建立了潜山复杂岩性识别图版。研究区多口探井应用该图版识别岩性，经钻后薄片等资料验证，岩性识别准确率达到了90.7%。

3）对应分析法将岩石岩性与矿物、元素反映在同一因子平面图上，便于统一进行地质解释和推断，根据载荷得分建立判别函数及识别图版，不仅具有严密的数理依据，还能赋予主因子较好的地质意义，便于潜山及上覆地层岩性复杂情况下的随钻快速识别，具有简单、实用、合理等优点。

图 1 ReliefF算法近邻样本选择示意

Figure 1. Neighbor sample selection for the ReliefF algorithm

下载: 全尺寸图片幻灯片

图 2 岩石岩性–成分对应分析载荷

Figure 2. Load for correspondence analysis of rock type and cuttings composition

下载: 全尺寸图片幻灯片

图 3 对应分析岩性识别图版

Figure 3. Lithology identification chart for correspondence analysis

下载: 全尺寸图片幻灯片

图 4 X3井元素及矿物变化综合柱状图

Figure 4. Composite bar chart of changes in elements and minerals of Well X3

下载: 全尺寸图片幻灯片

表 1 对应分析因子载荷

Table 1 Factor load for correspondence analysis

元素/矿物	H₁载荷得分	H₂载荷得分
铝	–0.155	0.049
钙	–0.081	–0.436
铁	–0.149	–0.028
镁	–0.125	–0.04
硅	0.126	0.525
钠	–0.061	–0.005
石英	1.808	0.373
长石	–1.076	0.802
方解石	0.139	–0.784
黏土	–0.425	–0.456

下载: 导出CSV

参考文献(20)

[1]	王长势,朱伟林,陈春峰,等. 东海丽水–椒江新生代凹陷基底的岩性及分布[J]. 同济大学学报(自然科学版),2014,42(4):636–644. WANG Zhangshi, ZHU Weilin, CHEN Chunfeng, et al. Basement lithology and distribution of Lishui-Jiaojiang Cenozoic Sag in East China Sea[J]. Journal of Tongji University(Natural Science), 2014, 42(4): 636–644.
[2]	夏斌,张敏强,万志峰,等. 东海丽水-椒江凹陷构造样式与含油气远景[J]. 华南地震,2007,27(3):1–8. XIA Bin, ZHANG Minqiang, WAN Zhifeng, et al. Structural styles and hydrocarbon prospects in the Lishui-Jiaojiang Sag, the East China Sea[J]. South China Journal of Seismology, 2007, 27(3): 1–8.
[3]	张建培,张田,唐贤君. 东海陆架盆地类型及其形成的动力学环境[J]. 地质学报,2014,88(11):2033–2043. ZHANG Jianpei, ZHANG Tian, TANG Xianjun. Basin type and dynamic environment in the East China Sea shelf basin[J]. Acta Geologica Sinica, 2014, 88(11): 2033–2043.
[4]	张胜利,夏斌. 丽水–椒江凹陷构造演化特征与油气聚集[J]. 天然气地球科学,2005,16(3):324–328. ZHANG Shengli, XIA Bin. Characters of tectonic evolution of the Lishui-jiaojiang sag and oil accumulation[J]. Natural Gas Geo-science, 2005, 16(3): 324–328.
[5]	郭明宇,李战奎,徐鲲,等. 渤中26-6构造太古界潜山储层含水识别方法[J]. 石油钻探技术,2023,51(3):137–143. GUO Mingyu, LI Zhankui, XU Kun, et al. Method of identifying water content in the Archaean buried hill reservoir of BZ 26-6 Structure[J]. Petroleum Drilling Techniques, 2023, 51(3): 137–143.
[6]	赵彦泽,李战奎,苑仁国,等. 太古界潜山界面卡取方法及应用[J]. 石油钻采工艺,2018,40(增刊1):55–57. ZHAO Yanze, LI Zhankui, YUAN Renguo, et al. Method and application of Archaean buried hill interface identification[J]. Oil Drilling & Production Technology, 2018, 40(supplement 1): 55–57.
[7]	王茂桢,王冰洁,杨传超,等. 辽东湾坳陷斜坡型太古界潜山储层特征及主控因素:以锦州25-A构造为例[J]. 断块油气田,2023,30(4):624–631. WANG Maozhen, WANG Bingjie, YANG Chuanchao, et al. Reservoir characteristics and main controlling factors of slope-type Archean buried hill in Liaodongwan Depression: A case study of Jinzhou 25-A Structure[J]. Fault-Block Oil & Gas Field, 2023, 30(4): 624–631.
[8]	程建,周卓明,段铁军,等. 梨树断陷基岩潜山油气成藏主控因素分析与勘探前景[J]. 特种油气藏,2020,27(4):26–32. CHENG Jian, ZHOU Zhuoming, DUAN Tiejun, et al. Main-controlling factor analysis of hydrocarbon accumulation in the bedrock buried hill of Lishu Fault Depression and its exploration prospect[J]. Special Oil & Gas Reservoirs, 2020, 27(4): 26–32.
[9]	周心怀,王清斌,冯冲,等. 渤海海域大型太古界潜山储层形成条件及地质意义[J]. 地球科学,2022,47(5):1534–1548. ZHOU Xinhuai, WANG Qingbin, FENG Chong, et al. Formation conditions and geological significance of large Archean buried hill reservoirs in Bohai Sea[J]. Earth Science, 2022, 47(5): 1534–1548.
[10]	刘杰,徐国盛,温华华,等. 珠江口盆地惠州26-6构造古潜山—古近系油气成藏主控因素[J]. 天然气工业,2021,41(11):54–63. LIU Jie, XU Guosheng, WEN Huahua, et al. Main factors controlling the formation of buried hill-Paleogene reservoirs in 26-6 Structure of Huizhou, Pearl River Mouth Basin[J]. Natural Gas Industry, 2021, 41(11): 54–63.
[11]	胡安文,牛成民,王德英,等. 渤海湾盆地渤中凹陷渤中19-6构造凝析油气特征与形成机制[J]. 石油学报,2020,41(4):403–411. HU Anwen, NIU Chengmin, WANG Deying, et al. The characteristics and formation mechanism of condensate oil and gas in Bozhong 19-6 Structure, Bozhong Sag, Bohai Bay Basin[J]. Acta Petrolei Sinica, 2020, 41(4): 403–411.
[12]	高德利,刘维,万绪新,等. PDC钻头钻井提速关键影响因素研究[J]. 石油钻探技术,2023,51(4):20–34. doi: 10.11911/syztjs.2023022 GAO Deli, LIU Wei, WAN Xuxin, et al. Study on key factors influencing the ROP improvement of PDC bits[J]. Petroleum Drilling Techniques, 2023, 51(4): 20–34. doi: 10.11911/syztjs.2023022
[13]	王亚萍,况雨春,杨高. 基于MATLAB的PDC钻头几何学仿真模型[J]. 西南石油大学学报,2007,29(增刊2):116–118. WANG Yaping, KUANG Yuchun, YANG Gao. The geometry emulation model of PDC bit by using MATLAB[J]. Journal of Southwest Petroleum University, 2007, 29(supplement 2): 116–118.
[14]	冯定. 涡轮钻具防斜打快钻井理论与技术研究[J]. 石油钻探技术,2007,35(3):9–11. FENG Ding. Theoretical and technical study of deviation control and fast drilling in turbodrill[J]. Petroleum Drilling Techniques, 2007, 35(3): 9–11.
[15]	王宏波,姚军,李双文,等. 利用对应分析法校正火成岩岩性识别图版:以黄骅凹陷为例[J]. 天然气地球科学,2013,24(4):719–724. WANG Hongbo, YAO Jun, LI Shuangwen, et al. The correction of correspondence analysis to the lithologic identification plate of igneous rocks in Huanghua Depression[J]. Natural Gas Geoscience, 2013, 24(4): 719–724.
[16]	吴欣松,吴胜和,聂昌谋,等. 对应分析方法在储集层评价中的应用[J]. 石油勘探与开发,1999,26(2):90–92. WU Xinsong, WU Shenghe, NIE Changmou, et al. Application of correspondence analysis in the evaluation of reservoir beds[J]. Petroleum Exploration and Development, 1999, 26(2): 90–92.
[17]	孙宁. 对应分析法在储层定量分类评价中的应用:以子长油田安定区长6储层为例[J]. 中国石油和化工标准与质量,2019,39(1):107–108. doi: 10.3969/j.issn.1673-4076.2019.01.053 SUN Ning. Application of correspondence analysis method in quantitative classification and evaluation of reservoir: A case study of Chang 6 Reservoir in Anding Area of Zichang Oilfield[J]. China Petroleum and Chemical Standard and Quality, 2019, 39(1): 107–108. doi: 10.3969/j.issn.1673-4076.2019.01.053
[18]	刘绍平,汤军,许晓宏. 数学地质方法及应用[M]. 北京:石油工业出版社,2011. LIU Shaoping, TANG Jun, XU Xiaohong. The methods and applications on mathematical geology[M]. Beijing: Petroleum Industry Press, 2011.
[19]	刘冬梅. 对应分析在航空安全事件研究中的应用[D]. 天津:中国民航大学,2016. LIU Dongmei. Research of aviation safety incidents based on correspondence analysis[D]. Tianjin: Civil Aviation University of China, 2016.
[20]	谭忠健,邓津辉,张国强,等. 渤海海域变质岩潜山储层有效性录井综合评价技术[J]. 特种油气藏,2023,30(5):11–17. TAN Zhongjian, DENG Jinhui, ZHANG Guoqiang, et al. Comprehensive evaluation technology of metamorphic submarine reservoir effectiveness mud-logging in Bohai Sea Area[J]. Special Oil & Gas Reservoirs, 2023, 30(5): 11–17.

施引文献(1)

期刊类型引用(1)

冯昊楠，杨森，王涛，王依言，曾星海，王方正. 基于RBF神经网络模型的天然气储层测录井岩性识别方法. 录井工程. 2025(01): 63-69+76 .

百度学术

其他类型引用(0)

资源附件(0)

图(4) / 表(1)

计量

文章访问数: 87
HTML全文浏览量: 6
PDF下载量: 34
被引次数: 1

1. 对应分析法原理及岩性识别图版
1.1 对应分析法原理
1.2 复杂岩性识别图版
2. 应用实例
3. 结　论

基于对应分析的丽水–椒江凹陷潜山岩性识别方法

计量

出版历程