Research on the Optimal Proportions of the New and Old Fractures in Refracturing of Horizontal Wells in Ultra-Low Permeability Reservoirs
-
摘要:
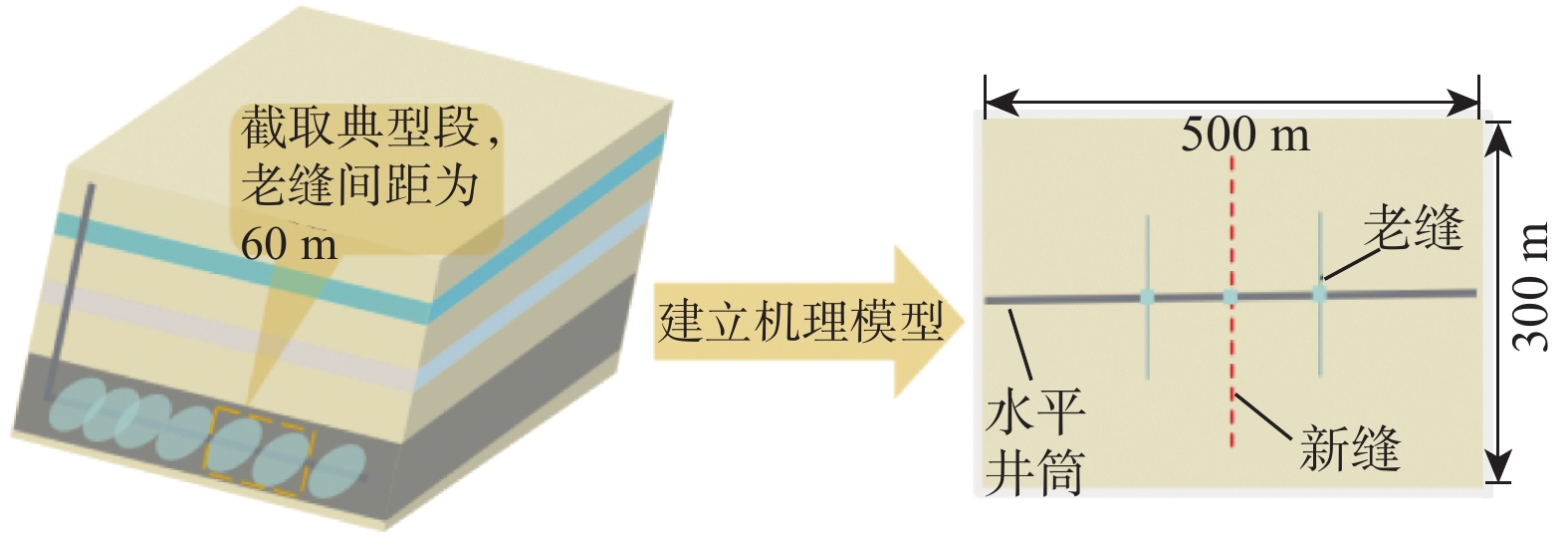
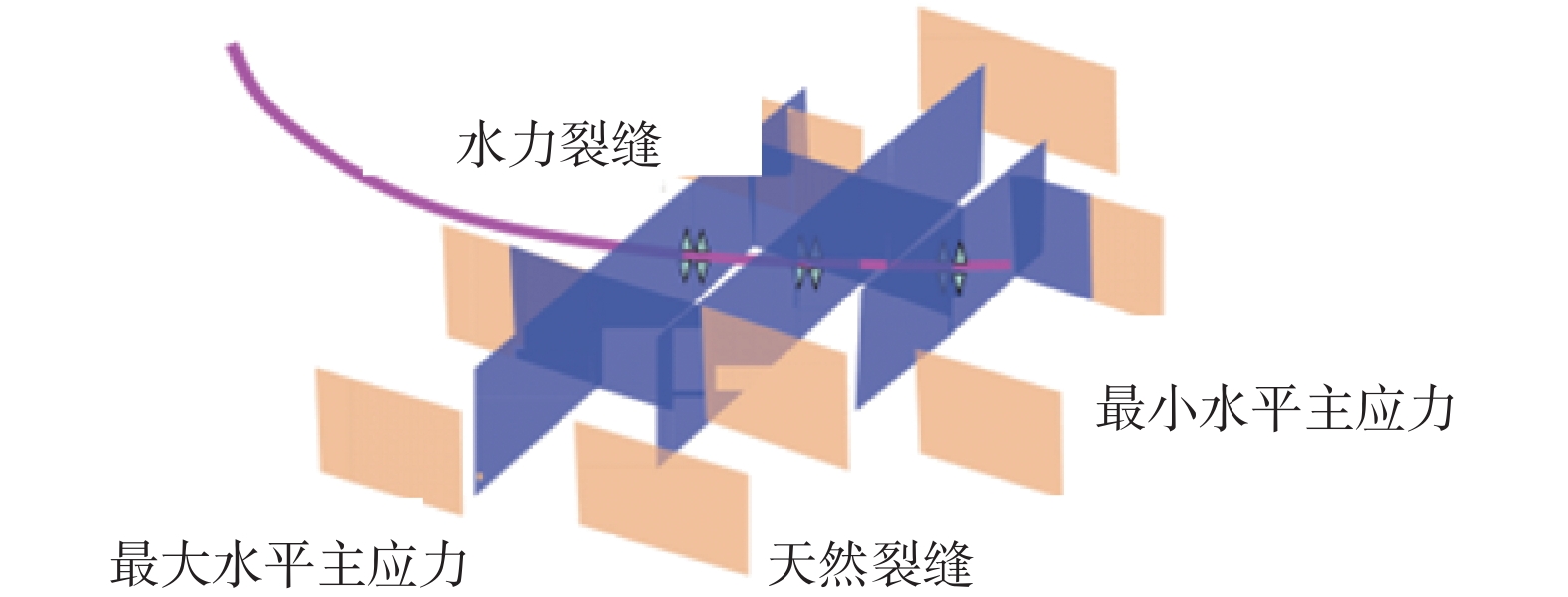
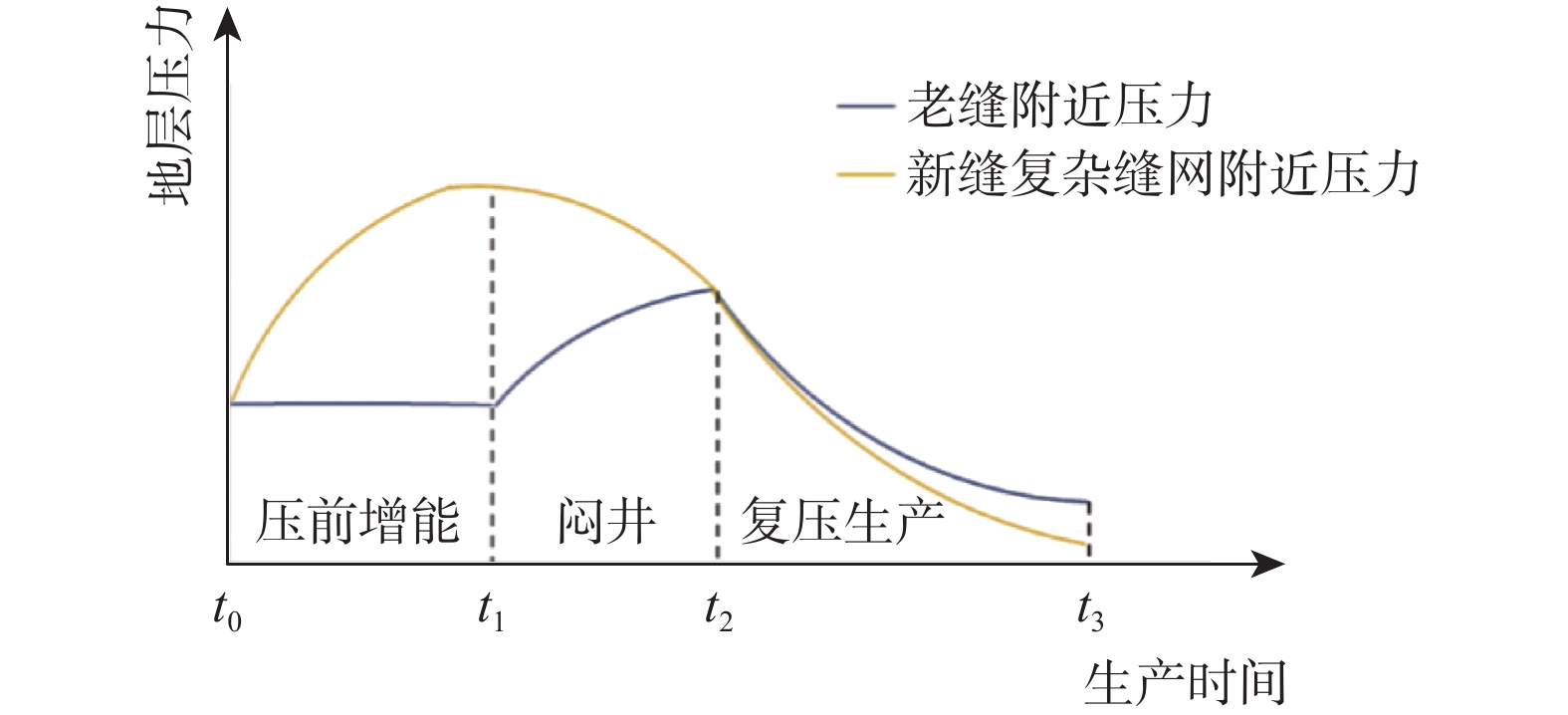
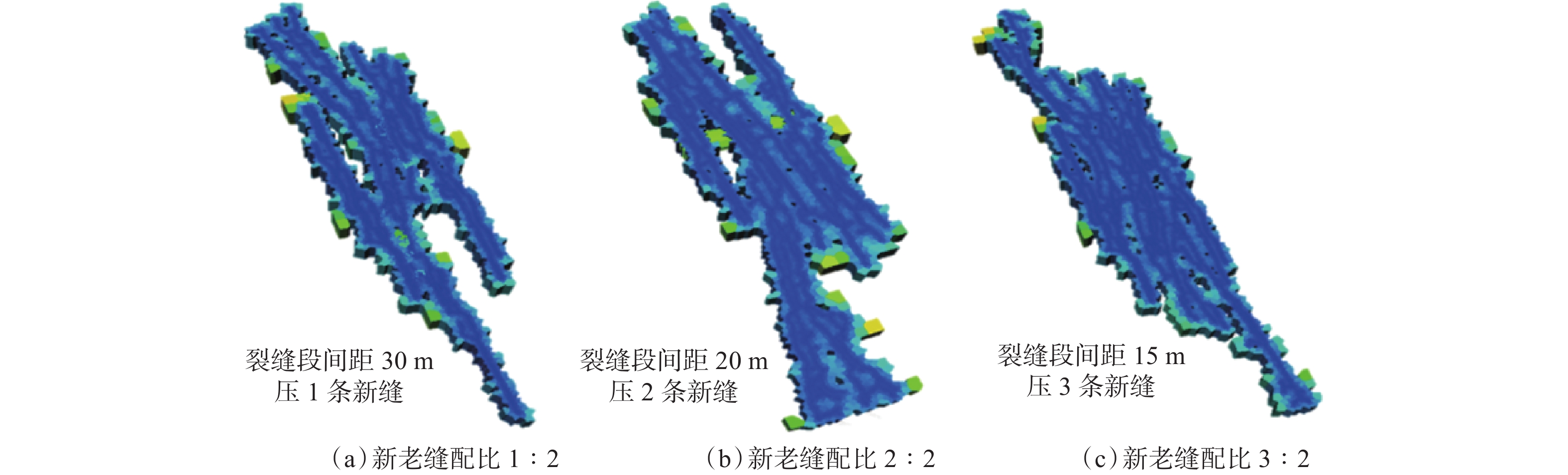
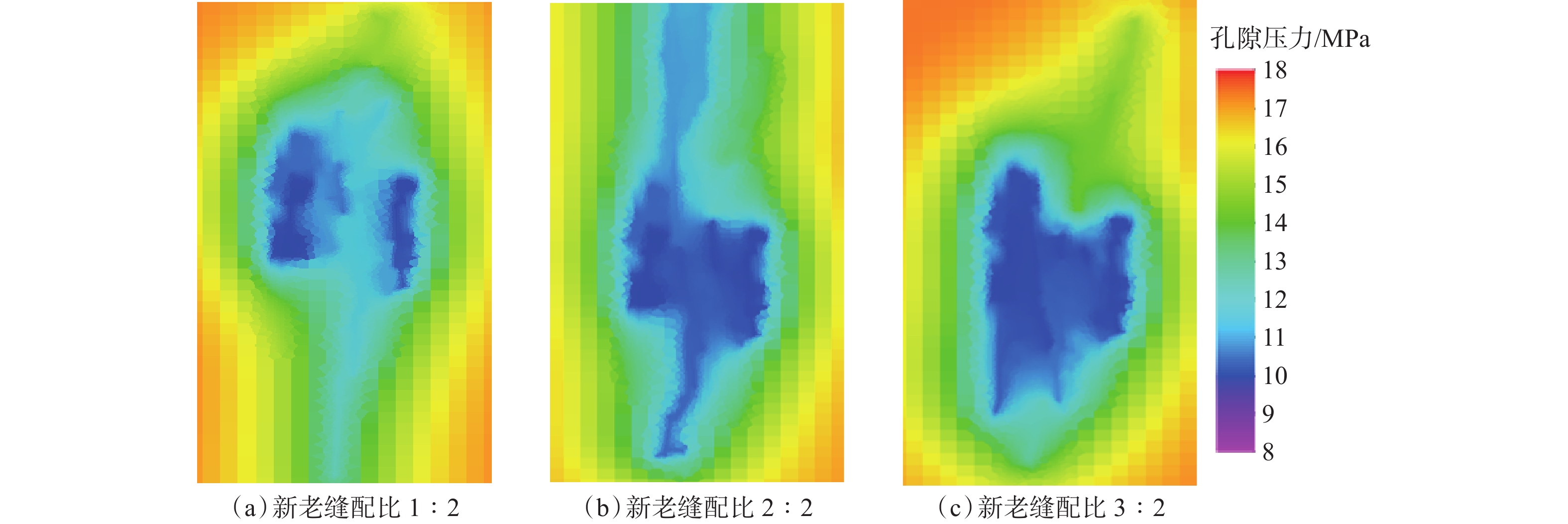
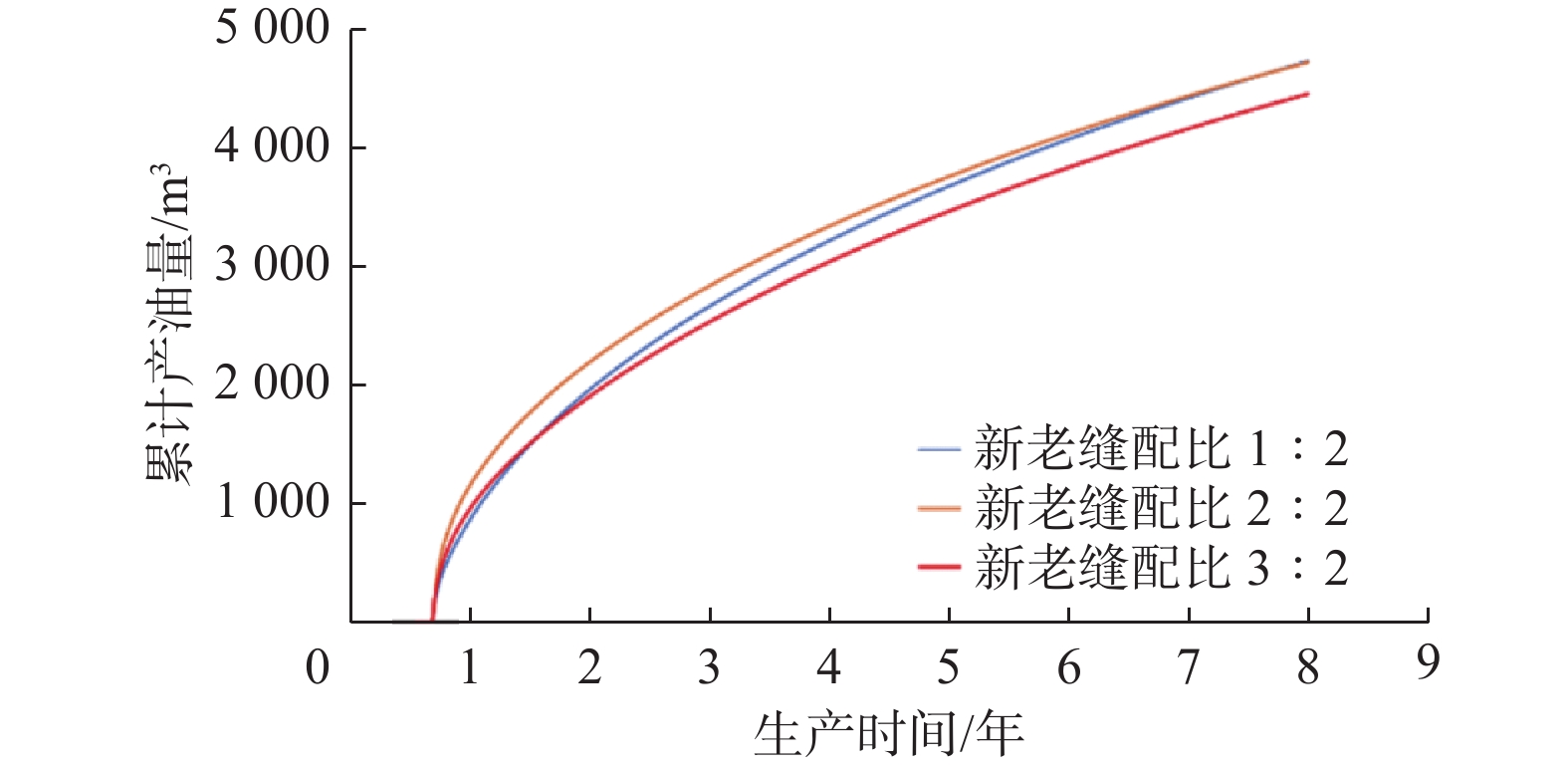
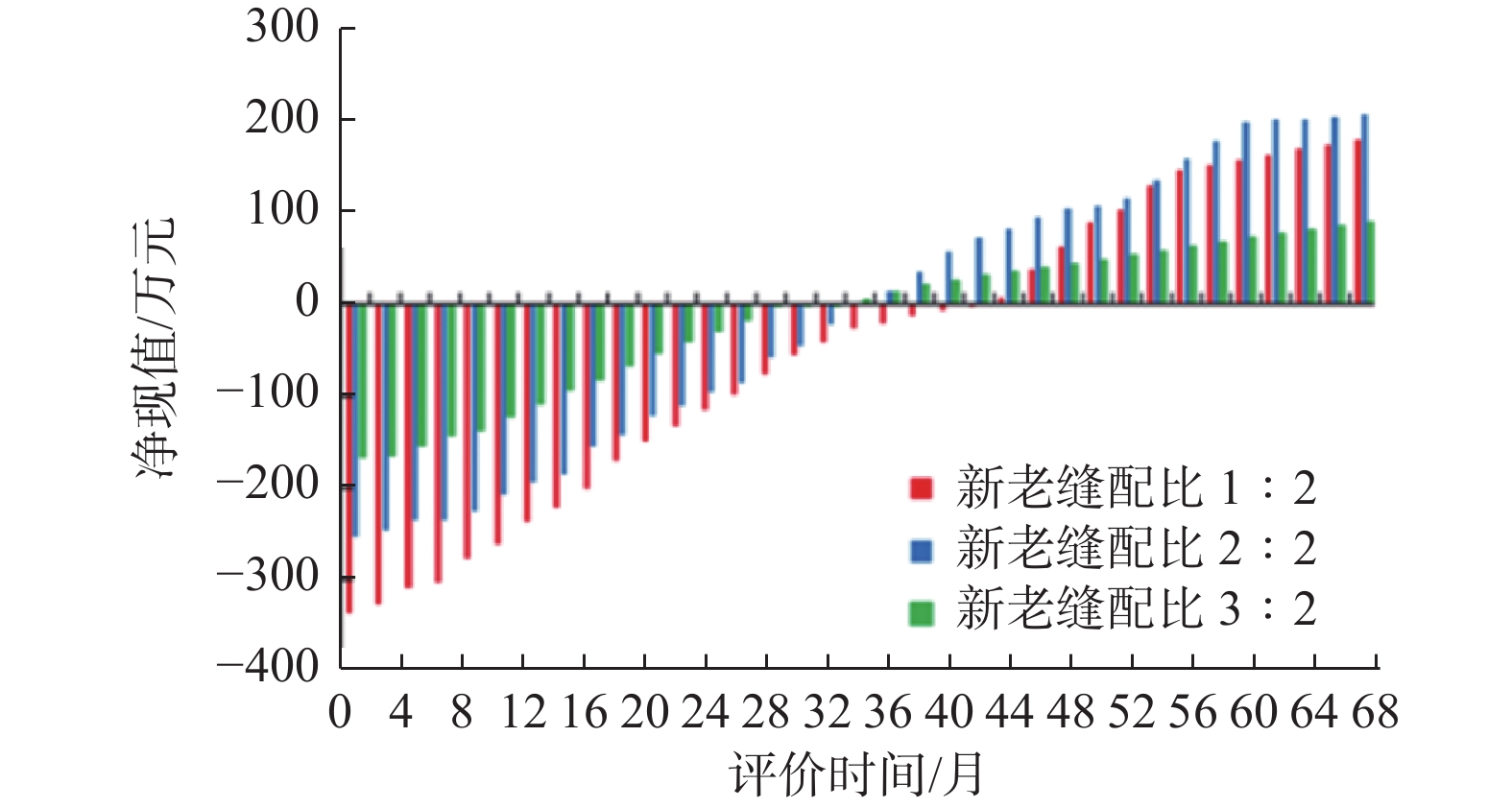
超低渗透油藏初次压裂投产后，由于地层能量亏空严重、裂缝失效等原因，油井产量递减迅速，无法满足生产需求，需要进行重复压裂，重复压裂设计的关键是确定合理的布缝位置和重复压裂的新缝数量。基于长庆油田元284井区储层地质特征，结合初次压裂生产情况，建立了水平井重复压裂裂缝延伸数值模拟模型；对比了不同新老缝配比条件下重复压裂储层改造体积与最终开采效果，明确了重复压裂前注水补能提高重复压裂改造效果的机理；通过分析经济收益，获得了合理的新老缝配比关系。模拟结果表明：重复压裂新缝为2条、缝间距为20 m时，更有利于形成复杂缝网，提高采收率；随着2条老缝间重复压裂新缝数量增加，更有利于裂缝间相互沟通形成复杂缝网，提高储层改造效果；老缝间重复压裂的新缝数量较多时，由于裂缝之间的相互干扰，会导致开发生产前期产量增幅递减，但随着不断生产，由于储层改造更为充分，对后期稳产较为有利。研究结果为超低渗透油藏水平井重复压裂方案设计提供了理论依据。
Abstract:After the initial hydraulic fracturing of the ultra-low permeability oil reservoir, there is a rapid decline in oil production due to the depletion of formation energy and fracture failure. This decline fails to meet the production demands, and the refracturing is needed. In the design of refracturing, the key lies in determining the optimal positioning and number of new fractures. In this study, a numerical simulation model for fracture extension during refracturing of horizontal wells was established, based on the geological characteristics of the Changqing yuan 284 well block oil reservoir and the production data from the initial hydraulic fracturing. A comparative analysis of the reservoir stimulation volume and ultimate developing effect was conducted with varying proportions of new and old fractures. The study found that energy replenishment by water injection before refracturing as a mechanism could effectively improve the reservoir stimulation effect of refracturing. Furthermore, an economic benefit analysis was performed to determine an reasonable proportion of new and old fractures. Simulation results indicated that a favorable condition for the formation of a complex fracture network and increased oil recovery was observed when there were two new fractures by refracturing, with a spacing of 20 m between fractures. As the number of new fractures between two old fractures increased, the formation of a complex fracture network and reservoir stimulation effect were further enhanced. However, a large number of new fractures between old fractures led to mutual interference, resulting in a decrease in the range of production increase during the early stage of development. Nonetheless, as development and production continued, there will be a more thorough reservoir stimulation effect, which is beneficial for stable production in the later period. These research findings offer a theoretical foundation for designing refrcuturing schemes for horizontal wells in ultra-low permeability oil reservoirs.
-
目前，渤海油田有45个油田正在生产，其中35个油田以人工水驱为主要开发模式。截至2018年底，渤海油田共有注水井787口，其中分层注水井742口，占比超过90%。国内对分层注水技术进行很多研究，并取得较好的现场应用效果[1–10]。渤海油田常用的分层注水技术有空心集成分层注水技术、同心分层注水技术、边测边调分层注水技术等，但在测调、验封时均需要钢丝或电缆作业配合，单井测调占用平台时间长。由于海上平台作业任务重，无法为钢丝、电缆调配作业提供足够的作业时间以及作业空间，同时大斜度井、水平注水井的井斜角超过60°，钢丝、电缆作业测调实施难度较大，导致近年来渤海油田分注井测试率和分注井层段合格率偏低，影响了分层注水开发效果。针对常规分层注水技术存在的问题，自2015年起渤海油田开始进行海上油田智能测调技术攻关，研制了三通结构带自锁无级调节的大排量测调工作筒，通过预置电缆的方式，实现了海上油田大排量远程电控直读注水，配套了适用于先期防砂完井方式下分层注水的分层密封工具，设计了防砂段内一体化电缆保护方案，形成了适用于海上油田先期防砂完井方式下分层注水的电缆永置智能测调关键技术[11–13]。现场应用表明，该技术可明显提高分层注水井测调效率和测调频次，为渤海油田高效开发提供了技术支持和保障。
1. 电缆永置智能测调技术原理
电缆永置智能测调分层注水技术，其井下工艺管柱主要由智能测调工作筒、过电缆插入密封、井下钢管电缆、过电缆定位密封、安全阀、滑套等组成，地面设备主要由地面控制器及控制计算机组成，如图1所示。空心集成分层注水技术等渤海油田常规分层注水技术中工作筒与配水器各自独立，调配时需通过钢丝作业逐级投放、打捞配水器并更换水嘴。电缆永置智能测调分层注水技术将工作筒与配水器合二为一，并将温度、压力、流量等测试单元集成于工作筒中随管柱一同下入井内，通过钢管电缆与地面控制器相连，地面控制器再通过无线或电缆等方式与平台中控室的控制计算机相连。采用电缆永置智能测调技术进行测调时，仅需通过控制计算机发送所需命令，地面控制器便会进行相应的编码、解码，并通过井下钢管电缆将信号传至井下智能测调工作筒，智能测调工作筒接到命令后进行相应动作并反向返回数据信息，经由地面控制器解码后反馈至控制计算机，实现远程智能测调。
![]()
图 1 电缆永置智能测调技术原理示意Figure 1. Schematic diagram of the cable implanted intelligent injection technology电缆永置智能测调技术适用于套管射孔完井及先期防砂完井的分层注水井，不受井斜限制，单层最大注入量800 m3/d，最大工作压力60 MPa，最高工作温度125 ℃，适用最大井深3 000.00 m。
2. 关键井下工具的研制
电缆永置智能测调分层注水的关键井下工具包括智能测调工作筒、过电缆密封工具和一体式电缆保护器，均为渤海油田自主研制。
2.1 智能测调工作筒
智能测调工作筒位于分层配水层段，其上部通过油管连接分层工具，是电缆永置智能测调技术的核心工具，其基本结构如图2所示。
![]()
图 2 智能测调工作筒结构示意1.下接头；2.下流量计；3.外套管；4.一体化可调水嘴；5.线路控制部；6.中心管；7.主体部；8.水嘴；9.管外压力计；10.管内压力计；11.上流量计；12.短外套管；13.上接头；14.电缆Figure 2. Schematic diagram of the intelligent monitoring/adjusting cylinder与常规分层注水工具相比，该智能测调工作筒内部元件繁多，在有限的空间里要集成测试、水嘴调节、线路控制、供电等功能，要实现工作筒与配水器的合二为一，需对该工具内部结构进行科学合理布局。
智能测调工作筒上接头下部与过流通道、上流量计相连。该工作筒采用高精度双电磁流量计，注入流体通过过流通道时由上流量计计量流入总流量，下流量计计量流出总流量，两者相减得到该层的实际注入流量。智能测调工作筒上部电缆插接于上接头，为智能测调工作筒供电，并于下接头处接出。该工作筒采用双压力计，压力计与上流量计下部相连，对称分布，分别负责测试管内压力和管外压力，验封时可根据管内外压力变化实现直读验封。管内压力计下部与一体化可调水嘴相连。一体化可调水嘴的结构如图3所示。
一体化可调水嘴为智能测调工作筒的唯一可动部件，为提高稳定性及耐久性，在其中设置了行程开关，水嘴全开或全关状态下能够自锁断电。中心过流通道在水嘴处分出支流通道，流体通过水嘴后进入地层，水嘴采用三通结构设计，选择耐冲蚀、耐震动和抗冲击性能好的氧化锆陶瓷材料，最大排量可达800 m3/d，且嘴损不超过1 MPa。为确定水嘴开度，在该水嘴磁钢下部设有一霍尔传感器。调节注水量时，电机带动丝杠转动，霍尔传感器通过计算减速器转动圈数确定水嘴开度，丝杠通过丝杠螺母副带动连杆进行直线运动，连杆带动陶瓷水嘴运动，从而改变出水孔漏出面积，最终实现注水量连续无级调节。一体化可调水嘴采用平衡压设计，试验证明在20 MPa压差下可顺利开启。线路控制部位于智能测调工作筒下流量计上部，负责数据存储和数据传输过程中的编码、解码等；同时，温度计集成于线路板上，负责环境温度测试。除可以手动测调外，智能测调工作筒还具有自动测调功能，现场应用时可根据实际需求进行选择。使用自动测调功能时，线路控制部接收地面命令确定需要的注入量，并与目前实际注入量进行比较，如超过设定的允许误差，线路控制部将控制电机转动调节一体化水嘴开度以使实际注入量符合要求，实现智能测调。
通过结构优化与材料优选，确定智能测调工作筒的外径116.0 mm，最大内通径44.0 mm，可进行氧活化等现场测试，最大单层排量800 m3/d，最大耐温125 ℃，耐压60 MPa，最大输出扭矩为8 N·m。
2.2 过电缆密封工具
与陆地油田不同，渤海油田分层注水井多为先期防砂完井，封隔器密封筒预置于防砂段内，通过配合使用定位密封和插入密封实现层间封隔。电缆作为电能和数据的传输介质需随智能测调工作筒下至防砂段内，为保证电缆顺利下入且不造成分层密封失效，必须研制开发具有穿越通道的过电缆密封工具。
过电缆密封工具主要由ϕ158.5 mm过电缆定位密封工具和ϕ120.7 mm过电缆插入密封工具组成，如图4所示。
过电缆定位密封工具的上接头、下接头分别与上、下端油管连接，定位体上设计有定位台阶，与顶部封隔器配合实现管柱定位，密封模块通过与顶部封隔器密封筒的过盈配合实现密封，隔环在密封模块之间起分隔作用，带固定螺钉的下接头用于固定定位密封本体上的密封模块组和隔环。在过电缆定位密封本体侧壁轴向设有供电缆穿过的过电缆通道，与常规定位密封不同，电缆可直接由密封本体侧壁穿过，电缆通道上、下两端分别设有NPT螺纹，与NPT扣配合可紧固电缆。设计的ϕ158.5 mm过电缆定位密封工具长1 441.00 mm，最大外径158.5 mm，最小内径76.0 mm，耐压30 MPa，上接头螺纹为ϕ88.9 mm UP TBG，下接头螺纹为ϕ73.0 mm TBG。
过电缆插入密封工具的结构与过电缆定位密封工具相似，不同之处在于其没有定位体，其他各部件的作用与过电缆定位密封工具相同。设计的ϕ120.7 mm过电缆插入密封工具长1 448.00 mm，最大外径120.7 mm，最小内径58.0 mm，耐压30 MPa，上接头螺纹为ϕ73.0 mm TBG，下接头螺纹为ϕ73.0 mm TBG。
2.3 一体式电缆保护器
防砂段内通径较小，电缆在随管柱下入过程中在油管接箍处可能会发生磕碰导致电缆损坏，同时还可能与井壁发生摩擦，导致电缆被刮伤。为了保证电缆在下入过程中可靠、安全，设计了防砂段油管一体式电缆接箍保护器，其组成如图5所示。
一体式电缆保护器在本体上开有4个对称的U形槽，在使用时该接箍保护器上、下端分别与油管连接，电缆在保护槽内通过，电缆通过时需剥除电缆外胶皮并将电缆塞入U形槽内，然后在U形槽旁的圆槽内塞入铜垫固定过盈胶条，再塞入2根过盈胶条，最后拧紧螺钉压帽挤压过盈胶条使其膨胀贴紧电缆以到达固定电缆的目的。设计的一体式电缆保护器最大外径116.0 mm，内径62.0 mm，长度235.0 mm，上下扣型为ϕ73.0 mm TBG，U形槽直径6.5 mm，适用于剥去胶皮后ϕ6.0 mm的钢管电缆。
3. 电缆永置智能测调工具性能试验
渤海油田单井增产增注措施实施频繁，对电缆永置智能测调工具整体的耐酸、耐压性能和水嘴的耐压差、耐卡性能要求较高。为了验证研制的电缆永置智能测调工具的相关性能，进行了地面性能试验。
3.1 耐酸试验
现场实践发现，电磁流量计电极在酸环境中会被腐蚀，造成井下工作筒短路，从而导致电缆永置智能测调工具出现故障。为此，对研制的智能测调工作筒进行了耐酸试验。
试验方法：按配方12.0%HCl+3.0%HF+0.5%缓蚀剂配制酸液，在模拟井内充满甘油（用于加热后油浴），将智能测调工作筒置于充满酸液的密封短节中并放入模拟井中；通过高压管线将泵与密封短节相连，用于维持系统压力；通过电缆将电源与电加热装置相连，用于维持系统温度；通过电缆将计算机与智能测调工作筒相连，用于实时监测工作筒的工作状态；做好上述工作后，保持密封短节内的压力为40 MPa，逐渐升高系统温度，对装有不同材质电极的智能测调工作筒进行耐酸试验。试验装置如图6所示，试验结果见表1。
![]()
图 6 智能测调工作筒耐酸试验装置Figure 6. Acid resistance test device for intelligent measuring and adjusting cylinder表 1 智能测调工作筒耐酸试验结果Table 1. Acid resistance test results of intelligent measuring/adjusting cylinder电极材料 试验压力/MPa 试验温度/℃ 试验时间/h 检测条件 结果 现象 钛 40 25 42 通电监测 短路 电极损坏 哈氏不锈钢B 40 40 38 通电监测 短路 电极断裂 哈氏不锈钢B 40 60 36 不通电监测 正常 通讯、密封良好 哈氏不锈钢C 46 90 228 通电监测 正常 通讯、密封良好 由表1可知：原用纯钛材质电极在酸环境中容易损坏；当采用哈氏不锈钢B作为电极材料时，在酸环境中不通电，智能测调工作筒的电极不会损坏；当采用哈氏不锈钢C作为电极材料时，在酸环境中通电测试、调节，智能测调工作筒的电极不会损坏。因此，现场应用时，电磁流量计电极的材料建议改用哈氏不锈钢C。
3.2 耐微压裂试验
微压裂增注是渤海油田主要增注技术之一，分层微压裂作业过程中非作业层需要保持水嘴全关状态，此时工作筒内外压差高达30 MPa，在这种状态下智能测调工作筒存在进液短路风险，同时也有损坏陶瓷水嘴的风险。因此，需要进行耐微压裂性能试验，来验证智能测调工作筒在微压裂作业过程中的可靠性。试验方法：关闭智能测调工作筒水嘴，通过泵注水使密封短节两端产生压差，在此期间持续通电进行监测，将压差稳定在45.0 MPa持续4 h以上时间后调节水嘴测试水嘴的开启情况。试验装置如图7所示，试验结果见表2。
![]()
图 7 智能测调工作筒耐微压裂、耐调剖性能试验装置Figure 7. Mini-fracturing and profile control resistance test device for intelligent measuring/adjusting cylinder表 2 智能测调工作筒耐微压裂试验结果Table 2. Results of micro-fracturing resistance test of intelligent measuring/adjusting cylinder压力（表A）/MPa 压力（表B）/MPa 持续时间/min 流量测试功能 压力测试功能 温度测试功能 30.2 0.3 5 正常 正常 正常 34.9 0.3 10 正常 正常 正常 40.1 0.4 20 正常 正常 正常 45.4 0.4 250 正常 正常 正常 由表2可知：将注入压力持续升至45.4 MPa，保持45.0 MPa压差250 min后，调节水嘴并测试水嘴功能，水嘴能够正常打开并能进行正向、反向调节；智能测调工作筒在45.0 MPa压差下，持续通电测试4 h以上时间后系统稳定、正常。试验后水嘴无损坏，可正常调节开度。由此可见，智能测调工作筒可满足渤海油田微压裂作业需求。
3.3 耐调剖试验
调剖是渤海油田提高采收率的主要增产措施之一，常用的凝胶型调剖剂黏度较大且具有弹性，通过水嘴时易堵塞水嘴造成憋压。因此，需要进行耐调剖性能试验，来验证智能测调工作筒在调剖作业过程中的可靠性。试验方法：将智能测调工作筒水嘴调至全开状态，向工作筒中持续泵注调剖剂，期间逐渐关小水嘴至30%开度，并监测智能测调工作筒电机电流是否出现异常（正常为25～40 mA，遇卡时电机电流增大），关小水嘴开度至20.0%后继续持续注入4 h以上时间，停注后测试水嘴开启情况。试验装置如图7所示，试验结果见表3。
表 3 智能测调工作筒耐微调剖性能试验结果Table 3. Results of fine profile control resistance test of intelligent measuring/adjusting cylinder注入时间/
min注入速度/
（m3·h－1）水嘴开度，
%电机电流/
mA电机
状态0 5.1 100 30.9 正常 10 5.4 85.0 30.9 正常 20 5.6 70.1 30.9 正常 28 5.6 46.2 30.3 正常 35 5.4 20.0 29.5 正常 279 5.2 20.0 29.7 正常 286 0 30.2 29.8 正常 291 0 50.3 30.9 正常 296 0 70.2 30.9 正常 304 0 91.2 30.9 正常 307 0 100 30.9 正常 由表3可知，注入过程中水嘴动作灵敏正常，持续注入超过4 h后未出现卡堵现象，水嘴可正常动作，各测试模块工作状态正常。由此可见，智能测调工作筒可满足渤海油田调剖作业需求。
4. 现场应用效果
截至2019年2月下旬，电缆永置智能测调技术在渤海油田累计应用38口井，最大分层数6层，最大下入深度3 333.00 m，最大井斜角87.62°，最大单层流量800 m3/d。已实施井应用电缆永置智能测调技术后，与应用常规分层注水技术相比，平均单井测调费用由十余万元降至0元，平均单井测调时间由4 d缩短至4 h，平均测调频次由不足1.0次/年提高至2.1次/年，达到了渤海油田分层注水井测试率指标要求，累计缩短平台占用时间300 d以上，节省测调费用900余万元。
以某油田A井为例，该井所在平台作业量大，无法为A井测调作业提供足够的作业时间及作业空间，2017年该井采用常规分层注水技术注水，未进行测调。2018年1月下入电缆永置智能测调管柱后，当年完成测调4次，节省测调费用50余万元，受益油井流压回升0.11 MPa，平均含水率下降2%，取得了很好的应用效果。
5. 结论与建议
1）相较于渤海油田常规分层注水技术，电缆永置智能测调技术无需钢丝或电缆作业配合，即可通过地面控制器进行远程操作来实现井下数据实时监测和井下流量实时控制，减少了测调作业时对平台时间、空间的占用，平均单井测调时间可缩短至4 h/井次。
2）通过持续的优化改进，电缆永置智能测调技术目前可满足渤海油田酸化、微压裂、调剖等增产增注作业需求，具有良好的适应性，为渤海油田稳油控水、改善水驱效果提供了技术保障。
3）稳定性与可靠性是电缆永置智能测调技术的关键，建议通过持续的应用、优化和改进，使该技术的稳定性及可靠性进一步提高，并形成多尺寸系列化智能测调工具，从而实现渤海油田分层注水井全覆盖。
-
![]()
图 2 压裂过程中水力裂缝与天然裂缝交互图
Figure 2. Interaction between hydraulic fractures and natural fractures during fracturing
![]()
图 3 压裂过程中水力裂缝与天然裂缝交互图
Figure 3. Interaction between hydraulic fractures and natural fractures during fracturing
![]()
图 4 注水补能前后孔隙压力分布
Figure 4. Pore pressure distribution before and after waterinjection for energy replenishment
![]()
图 5 注水补能前后应力阴影分布
Figure 5. Stress shading distribution before and after water injection for energy replenishment
![]()
图 6 注水补能前后两向应力差分布
Figure 6. Two-way stress difference distribution before and after water injection for energy replenishment
![]()
图 9 不同新老缝配比下的油井生产动态曲线
Figure 9. Oil well production dynamic curve with different proportions of new and old fractures
![]()
图 10 不同新老缝配比下的经济收益对比
Figure 10. Economic benefits change with different proportions of new and old fractures
表 1 不同新老缝配比下重复压裂裂缝延伸模拟参数
Table 1 Fracture extension simulation parameters with different proportions of new and old fractures
方案 裂缝导流能力/
（mD·m）单段裂缝
半长/m缝网复杂
程度新老缝配比1∶2 259.3 187.9 0.26 新老缝配比2∶2 216.8 156.6 0.28 新老缝配比3∶2 202.8 126.7 0.35 
下载: 导出CSV
表 2 不同新老缝配比下的储层改造体积
Table 2 Reservoir stimulation volume with different proportions of new and old fractures
方案 平均裂缝改造体积/
108m3总改造体积/
108m3新老缝配比1∶2 0.237 0.488 新老缝配比2∶2 0.139 0.529 新老缝配比3∶2 0.118 0.606
下载: 导出CSV
-
[1] 窦立荣,汪望泉,肖伟,等. 中国石油跨国油气勘探开发进展及建议[J]. 石油科技论坛,2020,39(2):21–30. DOU Lirong, WANG Wangquan, XIAO Wei, et al. Progress and suggestions on CNPC’s multinational oil and gas exploration and development[J]. Petroleum Science and Technology Forum, 2020, 39(2): 21–30.
[2] 韩頔. 低渗透油田开发的难点与挖潜对策分析[J]. 石化技术,2019,26(5):145–146. HAN Di. Difficulties in low permeability oilfield development and analysis of potential digging strategies[J]. Petrochemical Industry Technology, 2019, 26(5): 145–146.
[3] 马国财. 低渗透油藏地质特征与开发对策分析[J]. 化工设计通讯,2019,45(4):238. MA Guocai. Geological characteristics and development countermeasures of low permeability reservoirs[J]. Chemical Engineering Design Communications, 2019, 45(4): 238.
[4] 杨学峰,张斌,朱胜利,等. 超低渗透油藏开发初期降低递减对策分析[J]. 石油化工应用,2010,29(9):52–55. YANG Xuefeng, ZHANG Bin, ZHU Shengli, et al. Analysis of the countermeasures to reduce regression at the early stage of ultra-low permeability reservoir development[J]. Petrochemical Industry Application, 2010, 29(9): 52–55.
[5] 周波,叶凯,刘江. 水平井重复压裂改造工艺分析[J]. 中国石油和化工标准与质量,2022,42(3):180–182. ZHOU Bo, YE Kai, LIU Jiang. Analysis of refracturing modification process for horizontal wells[J]. China Petroleum and Chemical Standard and Quality, 2022, 42(3): 180–182.
[6] 贺代兰. 老井重复压裂工艺技术发展现状[J]. 科技和产业,2021,21(1):264–268. doi: 10.3969/j.issn.1671-1807.2021.01.048 HE Dailan. Study on the development of repeated fracturing technology in old wells[J]. Science Technology and Industry, 2021, 21(1): 264–268. doi: 10.3969/j.issn.1671-1807.2021.01.048
[7] BARREE R D, MISKIMINS J L, SVATEK K J. Reservoir and completion considerations for the refracturing of horizontal wells[R]. SPE 184837, 2017.
[8] 庞鹏,刘振宇,王胡振,等. 重复压裂改造时机数值模拟[J]. 大庆石油地质与开发,2015,34(6):83–87. PANG Peng, LIU Zhenyu, WANG Huzhen, et al. Numerical simulation of refracturing opportunity[J]. Petroleum Geology & Oilfield Development in Daqing, 2015, 34(6): 83–87.
[9] TAVASSOLI S, YU Wei, JAVADPOUR F, et al. Well screen and optimal time of refracturing: a Barnett shale well[J]. Journal of Petroleum Engineering, 2013, 2013: 817293.
[10] 霍雅迪,江厚顺. 一种基于BP神经网络的气井重复压裂井优选方法[J]. 天然气地球科学,2020,31(4):552–558. HUO Yadi, JIANG Houshun. A preferred method for gas well re-fracturing well based on BP neural network[J]. Natural Gas Geoscience, 2020, 31(4): 552–558.
[11] YANG Changdong, XUE Xu, HUANG Jixiang, et al. Rapid refracturing candidate selection in shale reservoirs using drainage volume and instantaneous recovery ratio[R]. URTEC-2459368-MS, 2016.
[12] TAO Liang, GUO Jianchun, ZHAO Zhihong, et al. Refracturing candidate selection for MFHWs in tight oil and gas reservoirs using hybrid method with data analysis techniques and fuzzy clustering[J]. Journal of Central South University, 2020, 27(1): 277–287. doi: 10.1007/s11771-020-4295-0
[13] WANG Zhiguo, LIU Zhongneng, GUI Jie, et al. A solution for mechanical isolation volume refracturing in ultra-low permeability horizontal wells: a case study in Ordos Basin[R]. IPTC-21155-MS, 2021.
[14] ARTUN E,KULGA B. 基于模糊推理的致密砂岩气储集层重复压裂井选择方法[J]. 石油勘探与开发,2020,47(2):383–389. doi: 10.1016/S1876-3804(20)60055-6 ARTUN E, KULGA B. Selection of candidate wells for re-fracturing in tight gas sand reservoirs using fuzzy inference[J]. Petroleum Exploration and Development, 2020, 47(2): 383–389. doi: 10.1016/S1876-3804(20)60055-6
[15] 郭建春,陶亮,曾凡辉. 致密油储集层水平井重复压裂时机优化:以松辽盆地白垩系青山口组为例[J]. 石油勘探与开发,2019,46(1):146–154. GUO Jianchun, TAO Liang, ZENG Fanhui. Optimization of refracturing timing for horizontal wells in tight oil reservoirs: a case study of Cretaceous Qingshankou Formation, Songliao Basin, NE China[J]. Petroleum Exploration and Development, 2019, 46(1): 146–154.
[16] 何海波. 致密油水平井缝网增能重复压裂技术实践[J]. 特种油气藏,2018,25(4):170–174. HE Haibo. Practice of re-fracturing with network energization for horizontal well in tight oil reservoir[J]. Special Oil & Gas Reservoirs, 2018, 25(4): 170–174.
[17] 蒋廷学,周珺,廖璐璐. 国内外智能压裂技术现状及发展趋势[J]. 石油钻探技术,2022,50(3):1–9. JIANG Tingxue, ZHOU Jun, LIAO Lulu. Development status and future trends of intelligent fracturing technologies[J]. Petroleum Drilling Techniques, 2022, 50(3): 1–9.
[18] JAYAKUMAR R, RAI R, BOULIS A, et al. A systematic study for refracturing modeling under different scenarios in shale reser-voirs[R]. SPE 165677, 2013.
[19] HUANG Jixiang, YANG Changdong, XUE Xu, et al. Simulation of coupled fracture propagation and well performance under different refracturing designs in shale reservoirs[R]. SPE 180238, 2016.
[20] 任佳伟,王贤君,张先敏,等. 大庆致密油藏水平井重复压裂及裂缝参数优化模拟[J]. 断块油气田,2020,27(5):638–642. REN Jiawei, WANG Xianjun, ZHANG Xianmin, et al. Refracturing and fracture parameters optimization simulation for horizontal well in Daqing tight oil reservoir[J]. Fault-Block Oil & Gas Field, 2020, 27(5): 638–642.
[21] 黄婷,苏良银,达引朋,等. 超低渗透油藏水平井储能压裂机理研究与现场试验[J]. 石油钻探技术,2020,48(1):80–84. HUANG Ting, SU Liangyin, DA Yinpeng, et al. Research and field test on energy storage fracturing mechanism of horizontal wells in ultra-low permeability reservoirs[J]. Petroleum Drilling Techniques, 2020, 48(1): 80–84.
[22] 胡春桥,任来义,贺永红,等. 鄂尔多斯盆地延长探区油气勘探历程与启示[J]. 新疆石油地质,2021,42(3):312–318. HU Chunqiao, REN Laiyi, HE Yonghong, et al. Petroleum exploration history and enlightenment of Yanchang exploration area in Ordos Basin[J]. Xinjiang Petroleum Geology, 2021, 42(3): 312–318.
[23] 达引朋, 陆红军, 杨博丽, 等. 低渗透老油田新型多缝重复压裂技术研究与应用[J]. 石油钻探技术, 2015, 43(3): 65-70. DA Yinpeng, LU Hongjun, YANG Boli, et al. Research and application of new refracturing technology in low permeability oilfield[J]. Petroleum Drilling Techniques, 2015, 43(3): 65-70.
[24] MASOULEH S F, KUMAR D, GHASSEMI A. Three-dimensional geomechanical modeling and analysis of refracturing and “frac-hits” in unconventional reservoirs[J]. Energies, 2020, 13(20): 5352. doi: 10.3390/en13205352
[25] HUBBERT M K, WILLIS D G. Mechanics of hydraulic frac-turing[J]. Transactions of the AIME, 1957, 210(1): 153–168. doi: 10.2118/686-G
[26] CIPOLLA C L, WARPINSKI N R, MAYERHOFER M J, et al. The relationship between fracture complexity, reservoir properties, and fracture-treatment design[J]. SPE Production & Operations, 2010, 25(4): 438–452.
[27] ZHU Haiyan, TANG Xuanhe, LIU Qingyou, et al. Complex fractures propagations of infill well based on reservoir stress evolution after long-time shale gas production[R]. ARMA-2019-0403, 2019.
-
期刊类型引用(44)
1. 方健. 油田注水系统智能化关键技术研究进展. 化工自动化及仪表. 2025(01): 1-9 . 
百度学术
2. 杜东哲，李兴，温仕娟. 井下无缆在线智能分注技术研究与应用. 石油化工自动化. 2025(01): 17-21 . 百度学术
3. 刘铁明，王柳，薛德栋，寇磊. 海上油田分层注气井下气体流量测试技术研究. 石油矿场机械. 2025(02): 7-14 . 百度学术
4. 窦金虎. 有缆智能一体化分注管柱在海上7″尾管注水井中的应用. 机电信息. 2024(08): 42-44 . 百度学术
5. 邹剑，刘长龙，张璐，张乐，陈征. 渤海油田智能分注技术研究现状及新进展. 中国海上油气. 2024(05): 170-177 . 百度学术
6. 刘义刚，刘长龙，张磊，张乐，薛德栋，徐元德. 海上油田压力波控制高效测调注水技术. 中国海上油气. 2024(05): 137-145 . 百度学术
7. 薛德栋，郭沛文，张成富，张磊，王瑶，沈琼，丁德吉. 渤海油田高效投捞无缆分注工艺研究及应用. 石油机械. 2024(10): 132-137 . 百度学术
8. 王勇，石张泽，卢晓辉. 有缆智能分层采油技术及其应用. 天津科技. 2024(12): 45-48 . 百度学术
9. 乔志学. 缆控智能分注技术现场试验与应用. 石油石化节能. 2023(03): 18-23 . 百度学术
10. 杨树坤，李越，廖朝辉，赵广渊，杜晓霞中. 渤海油田无缆智能分注技术优化及应用. 钻采工艺. 2023(03): 60-65 . 百度学术
11. 刘长龙，陈征，张乐，徐元德，蒋少玖，王威. 有缆智能配水器O形圈密封模拟研究. 液压气动与密封. 2023(08): 91-96 . 百度学术
12. 韩照阳，刘国振，张帅，吉洋. 过电缆压缩隔离密封工具研究与应用. 石化技术. 2023(10): 110-112 . 百度学术
13. 邹剑，刘长龙，郑灵芸，陈征，张伦玮. 井下永置式测调技术流量计研究现状及发展方向. 化工自动化及仪表. 2023(06): 729-735 . 百度学术
14. 孟祥海，夏欢，李彦阅，陈征，王楠，罗云龙，曹豹. 智能分注分采技术应用效果及其影响因素研究. 当代化工. 2022(01): 156-159 . 百度学术
15. 赵广渊，王天慧，杨树坤，李翔，吕国胜，杜晓霞. 渤海油田液压控制智能分注优化关键技术. 石油钻探技术. 2022(01): 76-81 . 本站查看
16. 王东，王良杰，张凤辉，杨万有，程心平. 渤海油田分层注水技术研究现状及发展方向. 中国海上油气. 2022(02): 125-137 . 百度学术
17. 朱孟涛，李杨杨. 渤海油田含硫化氢井修井技术. 天津化工. 2022(03): 102-104 . 百度学术
18. 陈征，刘长龙，张乐，徐元德，王威，蒋少玖，张志熊. 小尺寸高温电缆测调系统研究. 仪器仪表用户. 2022(07): 15-18+4 . 百度学术
19. 张乐，刘长龙，陈征，徐元德，王威，蒋少玖，张志熊. 小尺寸高温电缆测调工作筒技术研究. 仪器仪表用户. 2022(08): 1-4 . 百度学术
20. 宋铭. 单孔悬开式堵塞器及其应用. 化学工程与装备. 2022(07): 151-154 . 百度学术
21. 赵仲浩，黄新春，张成富，丁德吉. 海上油田分层采油井缆控对接式智能配产新技术. 中国海上油气. 2022(04): 213-217 . 百度学术
22. 杨玲智，周志平，杨海恩，李法龙，胡改星. 井下柔性复合管预置电缆数字式分注技术. 石油钻探技术. 2022(06): 120-125 . 本站查看
23. 王超. 偏心分层注水井一体化验封测调工具研制. 石油矿场机械. 2021(01): 73-76 . 百度学术
24. 毕天琪，杨晓东，田东海，牟燕. 智能分注分层流量自动比对测试技术研究与应用. 油气田地面工程. 2021(02): 11-14+21 . 百度学术
25. 邢晓光，方正，张辉，王鹏，王潇祎，郭玉廷. 智能分层射流泵排液技术. 油气井测试. 2021(01): 21-25 . 百度学术
26. 杨树坤，赵广渊，李啸峰，郭宏峰，杜晓霞，廖朝辉. 注水井智能无级调节配水器水嘴结构优选及评价. 河南科学. 2021(02): 196-203 . 百度学术
27. 谷元伟. 注水井智能分层测调技术的现场应用. 化学工程与装备. 2021(03): 27-28 . 百度学术
28. 孙林，李旭光，黄利平，夏光，杨淼. 渤海油田注水井延效酸化技术研究与应用. 石油钻探技术. 2021(02): 90-95 . 本站查看
29. 赵广渊，季公明，杨树坤，吕国胜，杜晓霞，郭宏峰. 液控智能分注工艺调配及分层注水量计算方法. 断块油气田. 2021(02): 258-261 . 百度学术
30. 张斌，左凯，李宁，齐海涛. 海上智能分层配注器研究. 中国石油和化工标准与质量. 2021(07): 51-52 . 百度学术
31. 陈征，张乐，蓝飞，张晓冉，宋鑫，张志熊，王威，徐元德. 渤海油田智能分注技术应用现状及发展前景. 辽宁化工. 2021(05): 623-626 . 百度学术
32. 孟祥海，陈征，蓝飞，张乐，张志熊，赵广渊. 无缆智能配水器流量测试系统的优化与改进. 北京石油化工学院学报. 2021(02): 19-23 . 百度学术
33. 杨树坤，李越，李翔，郭宏峰，季公明，史景岩. 渤海油田测调一体分注关键技术改进及应用. 石油化工高等学校学报. 2021(04): 91-96 . 百度学术
34. 李鹏伟，王建宁，姜燕，苏毅，张旭，赵非，陈军政. 桥式同心分注井验封测调一体化工具研制及应用. 石油矿场机械. 2021(05): 84-89 . 百度学术
35. 党博，王新亚，刘长赞，任博文，杨玲. 永置式智能井监测系统多层半双工通信技术. 仪表技术与传感器. 2021(10): 109-114 . 百度学术
36. 李耀泽. 注水井智能测调管柱的应用及故障分析. 石化技术. 2021(09): 107-108 . 百度学术
37. 何海峰. 胜利海上疏松砂岩油藏分层防砂分层采油技术. 石油钻探技术. 2021(06): 99-104 . 本站查看
38. 张智，杨昆，刘和兴，李磊，梁继文. 注水井井筒完整性设计方法. 石油钻采工艺. 2020(01): 76-85 . 百度学术
39. 郭宏峰，杨树坤，段凯滨，季公明，史景岩，安宗辉. 渤海油田可反洗测调一体分层注水工艺. 石油钻探技术. 2020(03): 97-101 . 本站查看
40. 徐兴安，张凤辉，杨万有. 海上油田注水井智能监测与控制技术研究. 当代化工. 2020(07): 1396-1399 . 百度学术
41. 刘义刚，孟祥海，张云宝，夏欢，曹豹，罗云龙. 海上油田分注分采效果及其影响因素数值模拟——以渤海SZ36–1油田为例. 石油地质与工程. 2020(04): 95-101 . 百度学术
42. 肖国华，黄晓蒙，李会杰，关海峰. 直读测调偏心恒流配水器研制. 特种油气藏. 2020(05): 151-156 . 百度学术
43. 夏欢，刘义刚，孟祥海，张志熊，蓝飞，曹豹，罗云龙. 分层注水配注方法及其影响因素数值模拟研究. 辽宁化工. 2020(12): 1567-1573 . 百度学术
44. 刘佳. 影响注水井洗井质量的因素分析. 化学工程与装备. 2019(07): 144-145 . 百度学术
其他类型引用(9)
计量
- 文章访问数: 207
- HTML全文浏览量: 73
- PDF下载量: 63
- 被引次数: 53
