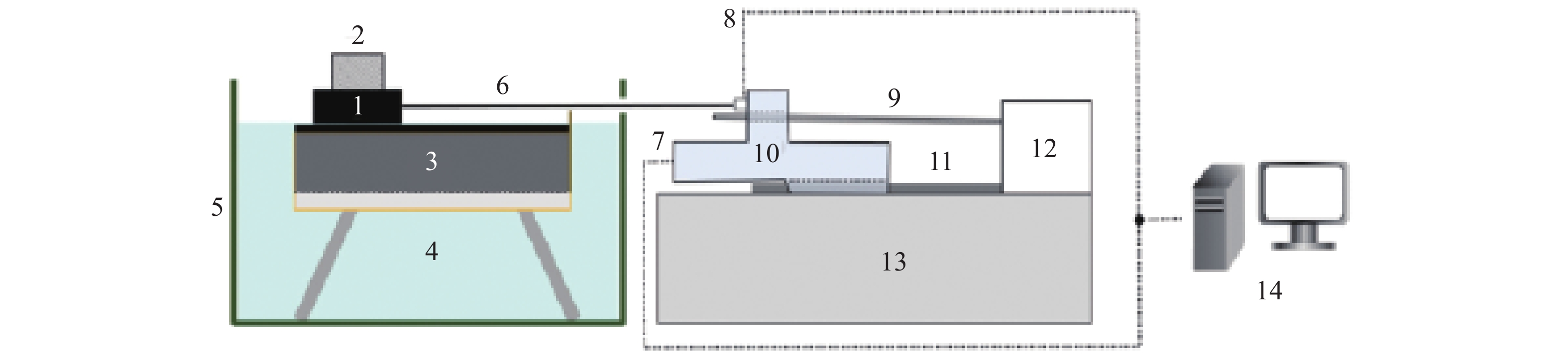
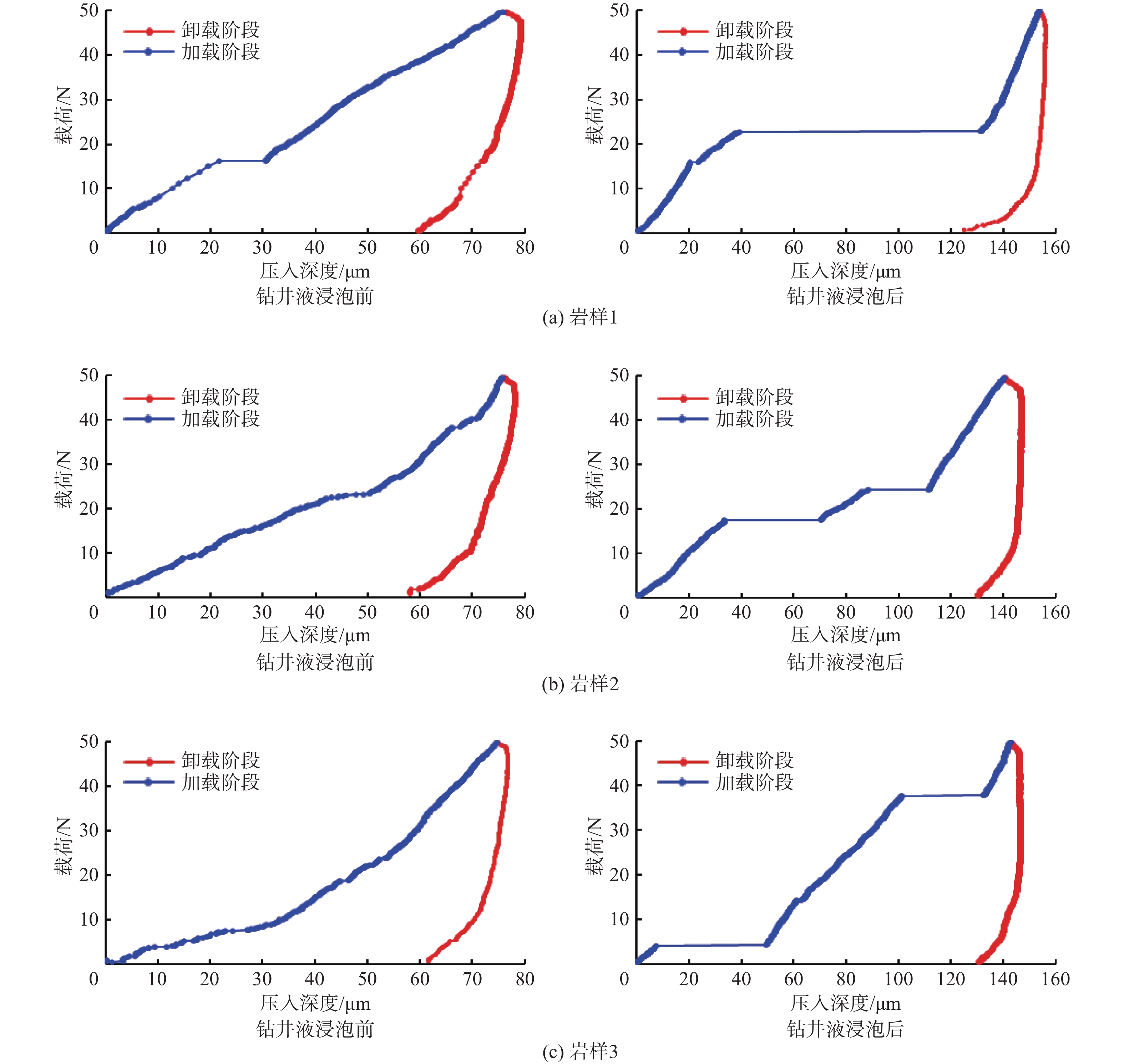
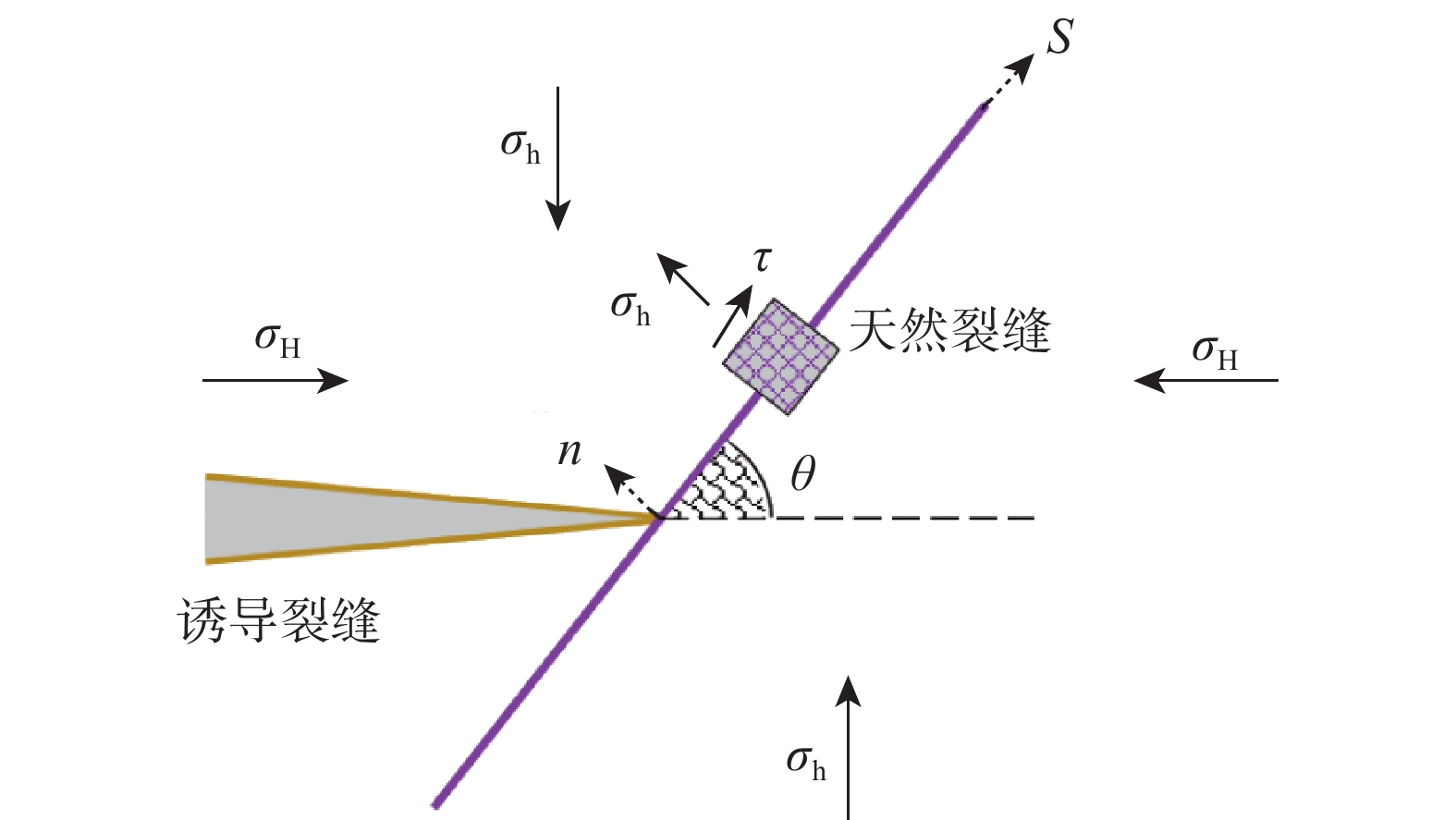
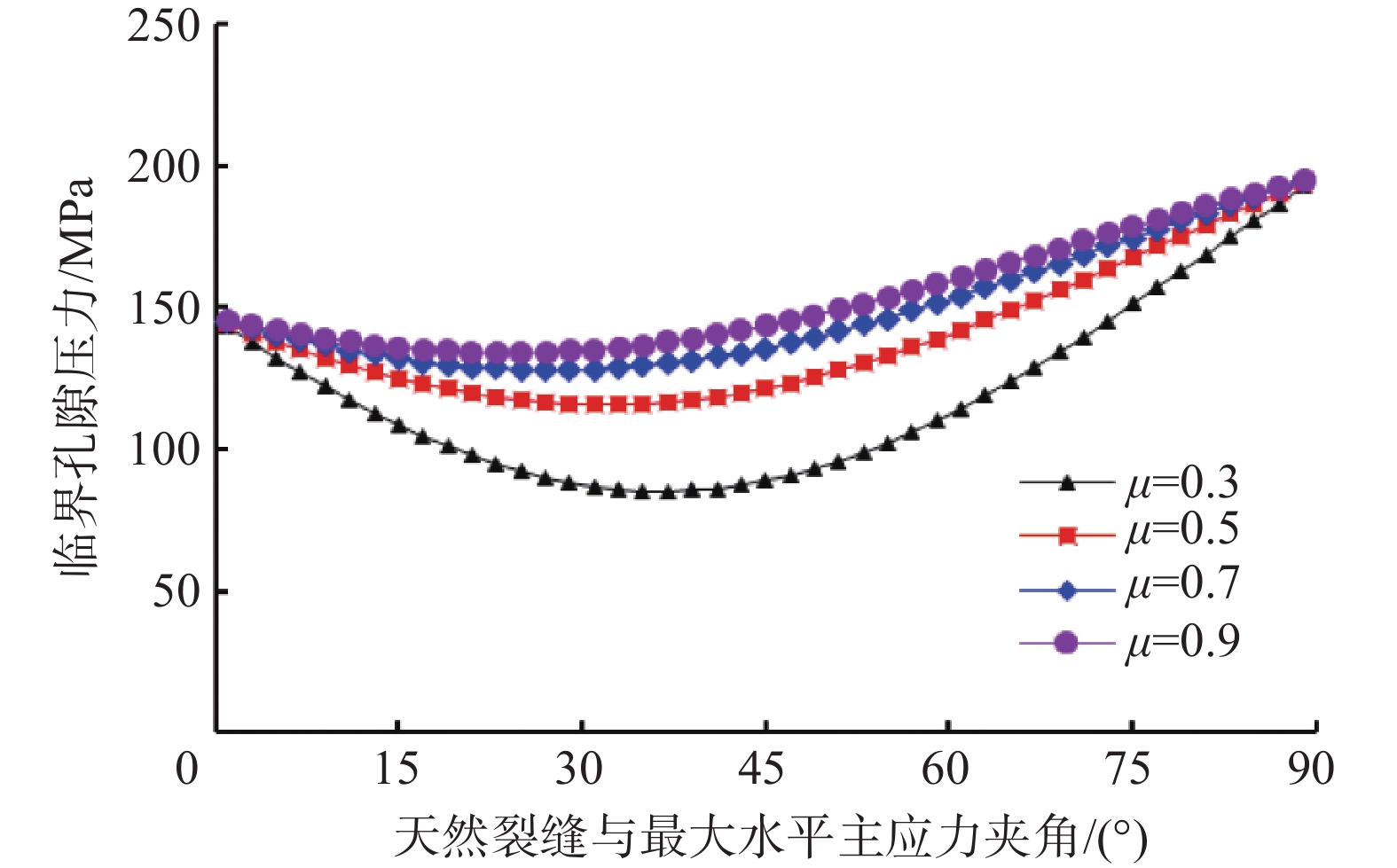
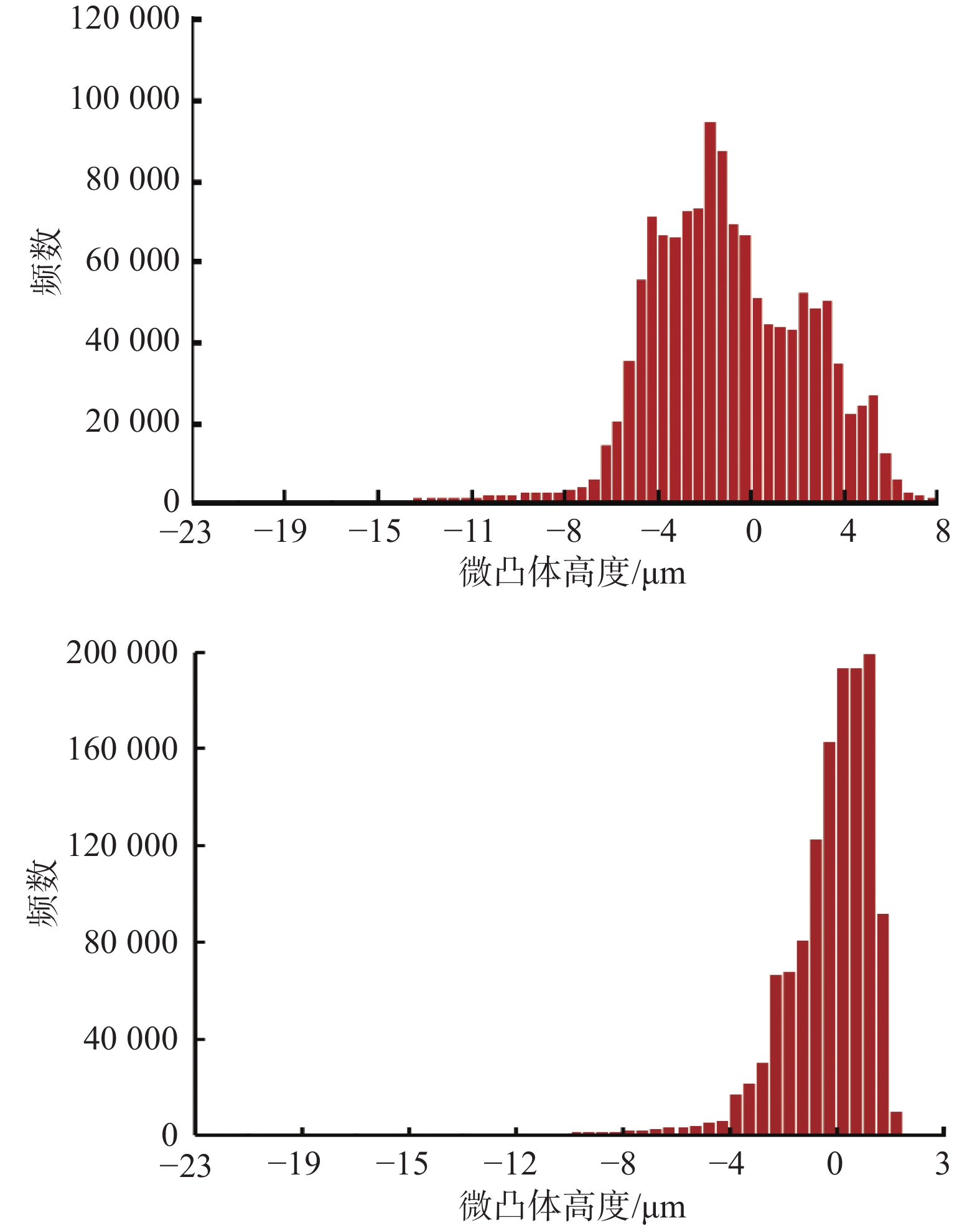
Friction & Sliding on Fracture Surfaces: A New Mechanism for Increasing Drilling Fluid Leakage in Deep Fractured Reservoirs
-
摘要: 针对深层裂缝性地层在初次堵漏失败后多发生漏失量更大的重复性漏失的问题,设计并进行了裂缝面间摩擦滑动(简称缝面摩滑)前后的裂缝封堵模拟试验,以钻井液环境下岩板与岩块的摩擦滑动试验、基于微压痕的岩石力学参数测试、表面三维扫描等手段为辅,分析了钻井液侵入对天然裂缝缝面摩滑的诱发作用,探讨了缝面摩滑对裂缝性储层钻井液漏失的影响。油基钻井液或水基钻井液侵入天然裂缝,均能使岩石缝面摩擦因数减小,油基钻井液使岩石缝面摩擦因数减小的作用更强,这会诱发缝面摩滑形成错位裂缝,为钻井液漏失加剧提供通道和空间;缝面摩滑可使裂缝渗透率升高,导致钻井液封堵能力降低,钻井液漏失加剧;摩滑后缝面更光滑,可能会进一步扩大错位程度,使裂缝长度和宽度大幅增大,造成钻井液漏失加剧。研究结果表明,缝面摩滑是导致深部裂缝性地层钻井液漏失加剧的原因之一,提高天然裂缝面之间的摩擦因数、有效控制缝面摩滑可控制深部裂缝性地层的钻井液漏失。Abstract: Because repetitive leakage in greater volume often occurs in deep fractured reservoirs after the failure of initial plugging, fracture plugging simulation before and after the sliding with friction happens on fracture surfaces (referred to as friction & sliding on fracture surfaces) was designed and carried out. Supported by the friction & sliding experiments of rock plates and blocks in drilling fluid environment, rock mechanics parameter test based on micron indentation and the three-dimensional surface scanning, the inducing effect of drilling fluid intrusion on the friction & sliding on fracture surfaces was analyzed, and the influence on drilling fluid leakage in fractured reservoirs brought by friction & sliding on fracture surfaces was explored. Experiments showed that when the drilling fluid invaded natural fractures, both oil-base and water-base drilling fluids could decrease the friction factors of fractured rock surfaces, and the oil-base drilling fluid could brought a stronger effect, which would induce friction & sliding on fracture surfaces to form dislocated fractures, providing channels and space for the aggravation of drilling fluid leakage. Also, friction & sliding on fracture surfaces can increase the permeability of fractures, resulting in a decrease in the plugging capacity of drilling fluid and increasing drilling fluid leakage. Moreover, fracture surfaces were smoother after friction & sliding, which may further intensify the degree of dislocation. With the huge increase in the length and width of fractures, the leakage of drilling fluid was exacerbated. The research results showed that friction & sliding on fracture surfaces was one of the reasons for the exacerbation of drilling fluid leakage in deep fractured reservoirs. Drilling fluid leakage in deep fractured reservoirs could be controlled by increasing the friction factors of natural fracture surfaces and effectively controlling the friction & sliding on fracture surfaces.
-
Keywords:
- deep part /
- fractured reservoir /
- friction /
- sliding /
- drilling fluid leakage /
- mechanism
-
井筒温度场的预测贯穿钻井和固井全过程,对流体性能参数的确定和井筒压力的计算具有重要意义,也是其他相关研究的重要基础[1–2]。目前,对于钻井期间的井筒温度场,国内外学者进行了大量理论研究并研制了MWD等测温设备,形成了较为成熟的预测方法[3–8]。而在固井循环期间,由于无法下入温度测量装置,温度场的获取依赖于通过数学模型进行预测,这对预测模型的精度提出了较高的要求,尤其是随着勘探开发向深水领域进军,固井井筒温度场的准确预测愈发重要。
目前,现场常用的注水泥温度预测方法是1941年美国石油学会提出的API方法[9],然而该方法预测的温度场普遍偏高,使得设计的水泥浆过分缓凝,大大降低了固井质量。1990年,S. H. Bittleston等人[10]利用经验系数对API方法中的模型进行了修正,但修正后的模型考虑的因素较少,仅适用于少数区块。随后,经过Frederic Guillot、尹成和刘洋等人[11–13]的不断改进,其精度和适用性不断提高,不过这些模型仅适用于陆上固井。2019年,赵琥等人[14]对影响深水固井井筒循环温度场的因素进行了研究,为水泥浆参数的设计提供了理论基础。2020年,郝锋等人[15]重点考虑水泥水化热对温度场的影响,建立了固井井筒温压耦合计算模型,研究表明,固井注水泥过程中,井底温度呈现先降低后小幅度升高的趋势,该模型预测结果比常规模型更精确。此外,R. L. Dillenbeck、杨志伏、王雪瑞等人[16–18]在考虑水泥水化反应的基础上,对固井候凝期间的温度场进行了大量研究。
综上可知,现有文献侧重于对陆上固井和候凝阶段温度场的研究,而对深水固井循环温度场的研究较少,相关理论模型仍处于发展阶段、模型计算精度有待提高。为此,笔者考虑井身结构对传热系数的影响、流体热力学参数差异及其随环境变化的特点,结合流体界面位置描述方程,建立了适用于深水固井循环阶段井筒温度场的预测模型,同时利用模型分析了关键影响因素。
1. 深水固井井筒流体流动物理模型
根据循环流体的类型可以将固井循环过程分为钻井液循环和水泥浆注入2个阶段,针对这2个阶段分别建立对应的物理模型。
1.1 钻井液循环阶段
图1所示为钻井液循环阶段井筒内流体流动物理模型。在钻井液循环阶段,钻井液从井口进入套管,再由环空返回钻井液池。循环过程中,不同井深处流体所处区域不同,根据井身结构的特点将其分为4个区域,分别是海水区、水泥环区、套管段和裸眼段。不同区域处流体(钻井液、海水、环空流体)和固体(套管、水泥环、地层)的导热系数、对流换热系数、比热容等热力学参数均不相同,因此建立温度场预测模型时中必须考虑这些区域的差异对传热过程的影响[19]。
1.2 水泥浆注入阶段
图2所示为水泥浆注入阶段井筒内流体流动物理模型。在水泥浆注入阶段,从井口依次注入隔离液、冲洗液、水泥浆,随后再次注入钻井液进行顶替。由于注入流体的类型较多且性能差异大,该阶段温度场的变化比钻井液循环阶段更为复杂。在水泥浆注入阶段,随着注入时间增长,不同类型流体的位置不断变化,因此必须对不同类型流体的界面位置进行追踪,以便准确地模拟固井水泥浆注入阶段井筒的传热过程。
2. 深水固井井筒温度场预测数学模型
2.1 基本假设
固井井筒温度场的影响因素较多,为便于建立模型和后续求解,作出如下假设:同一区域固井流体的温度场仅在轴向上发生变化;海水和地层的热物性参数(密度、比热和导热系数)为恒定值[20];忽略套管偏心的影响,注入阶段的顶替过程为稳态顶替;海水区忽略隔水管周围海水温度的径向变化;水泥环内边缘到水泥环外边缘的传热过程为稳态传热,水泥环外边缘到地层的传热过程为非稳态传热[21],如图3所示(
θa 为环空内流体温度,℃;θwB 为环空B的温度,℃;θwo 为水泥环区外缘温度,℃)。2.2 瞬态传热数学模型
以不同区域处的微元体为研究对象,建立对应的能量守恒方程,用于描述固井循环过程中的传热过程。
2.2.1 套管内流体的能量守恒方程
套管内流体的传热过程包括流体间的热传导、流体与套管内壁的热传导、流体与套管内壁的强制对流换热以及摩擦产生的热源,数学模型为:
Qci+κl∂2θci∂z2−ql∂(ρlclθci)∂z−2π rcihci(θci−θc)=π r2ci∂(ρlclθc)∂t (1) 式中:
Qci 为流体与套管内壁的摩阻热源,W/m;κl 为流体导热系数,W/(m·℃);θci 和θc 分别为套管内流体温度和套管壁温度,℃;z为井深,m;ρl 为流体密度,kg/m3;ql 为流体的流量,m3/s;cl 为流体比热容,J/(kg·℃);rci 为套管内径,m;hci 为套管内壁对流换热系数,W/(m2·℃)。2.2.2 套管能量守恒方程
套管的传热过程包括套管间的热传导、流体与套管壁的强制对流换热,数学模型为:
κc∂2θc∂z2+2rcihci(θci−θc)r2co−r2ci−2rcohco(θc−θa)r2co−r2ci=∂(ρcccθc)∂t (2) 式中:
κc 为套管导热系数,W/(m·℃);ρc 为套管密度,kg/m3;cc 为套管比热容,J/(kg·℃);rco 为套管外径,m;hco 为套管外壁对流换热系数,W/(m2·℃)。2.2.3 环空内流体的能量守恒方程
环空内流体的传热过程包括流体间的热传导、流体与套管外壁和井壁的强制对流换热和摩擦产生的热量。此外,传热过程还包括流体与不同区域处固体的强制对流换热。对于不同区域处的固体,虽然其温度场
θx(r,h,t) 的变化规律及其对应的数学描述方程不同,但其与环空流体的传热学模型是相似的,数学模型为:Qa−κl∂2θa∂z2+ql∂(ρlclθa)∂z−2raihax(θx−θa)r2ax−r2co+2rcohco(θc−θa)r2ax−r2co=∂(ρlclθa)∂t (3) 式中:
Qa 为流体与套管外壁和井壁的摩阻热源,W/m;θx 为x区域井壁处的温度,℃;rax 为x区域的井径,m;hax 为x区域井壁的对流换热系数,W/(m2·℃)。2.2.4 不同区域处地层或海水对应的传热学模型
基于模型假设,考虑不同区域间井身结构的差异和不同区域处流体和固体导热系数、对流换热系数、比热容等热力学参数的差异,建立如下传热学模型,用于计算温度场
θx(r,h,t) 。海水区由于有海水的存在,其温度场的变化与水泥环区、套管段地层和裸眼段地层相差较大。
κs(∂2θs∂r2s+∂2θs∂z2)+κsrs∂θs∂rs−qs∂(ρscsθs)∂z=∂(ρscsθs)∂t (4) 式中:
κs 为海水导热系数,W/(m·℃);θs 为海水温度,℃;rs 为海水距离井眼轴线的距离,m;ρs 为海水密度,kg/m3;qs 为海水流量,m3/s;cs 为海水比热容,J/(kg·℃)。参照文献[22]建立水泥环区不同环空处的温度场模型。以环空B为例(见图3),基于稳态和瞬态传热理论,推导环空温度场预测模型,其他环空与此类似。
稳态区总传热系数的计算公式为:
hto=(3∑n=1raoranhan+3∑j=1raolnrojrijkcj+3∑m=1raolnromrimκsm)−1 (5) 式中:
hto 为水泥环稳态区总传热系数,W/(m2·℃);ran 为第n个环空距离井眼轴线的距离,m;han 为第n个环空的传热系数,W/(m2·℃);roj和rij 分别为第j层套管的外径和内径,m;κcj 为第j层套管的导热系数,W/(m·℃);rom 和rim 分别为第m层水泥环的外径和内径,m;κsm 为第m层水泥环的导热系数,W/(m·℃)。稳态区外缘温度的计算公式为:
θwo=θfκf+θaraohtof(t)κf+raohtof(t) (6) 式中:
θf 为地层温度,℃;κf 为地层的导热系数,W/(m·℃);f(t) 为无因次地层导热时间函数。环空B温度的计算公式为:
θwB=θwo+raohtolnraoRB(θf−θwo)κl (7) 式中:
RB 为环空B的外径,m。套管段地层可看作只有一级水泥环的水泥环区,该区域的温度场可通过式(5)—式(7)进行计算。
裸眼段地层的流体与地层直接接触,地层中只考虑轴向和径向的热传导,该区域地层温度场的控制方程为:
∂2θf∂z2+∂2θf∂r2+1r∂θf∂r=ρfcfκf∂θf∂t (8) 式中:
ρf 为地层岩石密度,kg/m3;cf 为地层比热容,J/(kg·℃)。2.3 水泥浆注入阶段界面位置描述方程
钻井液循环阶段,井筒内只有一种流体,因此不存在由于多流体间性能差异而引起的界面形状不断变化的问题。而在水泥浆注入阶段,不同类型流体间存在一个(顶替)界面(钻井液/前置液界面、前置液/水泥浆界面、水泥浆/钻井液界面),该界面在稳态条件下会由平面逐渐发展为不规则的曲面[23],描述该界面形状的公式为:
Δρlig(h2ix+r2ax)+12ΔpΔL(r2ax−r2co)+τ(rco−rax)=0 (9) 式中:
Δρli 为第i个界面两侧流体密度差,kg/m3;hix 为第i个界面位置,m;Δp 为界面压差,MPa;ΔL 为界面长度,m;τ 为壁面剪切力,Pa。第i个界面平均位置
¯hi 的计算公式:¯hi=∫t0vldt+∫∫◯rxhix (10) 式中:
vl 为流体的流速,m/s;¯hi 为第i个界面的平均位置,m。将式(9)代入式(10),则可以得到流体顶替界面位置与流体注入时间的变化关系。
2.4 对流换热系数与比热容
2.4.1 对流换热系数
对流换热系数是努塞尔数、导热系数和流道当量直径的函数,其计算公式为:
h=NuκDh (11) 式中:
h 为对流换热系数,W/(m2·℃);Nu 为努塞尔数;κ 为导热系数,W/(m·℃);Dh 为当量直径,m。努塞尔数与流体的流态和流动环境有关,对于不同区域,努塞尔数的计算方法不同[24]。套管内流体努塞尔数的计算公式为:
Nu=4.364(3n+14n)0.323 (12) 环空内流体努塞尔数的计算公式为:
Nu=1.86(Repr)1/3(DhL)1/3 (13) 式中:L为环空流道长度,m。
海水区海水努塞尔数的计算公式为:
Nu=0.3+0.62Re1/2p1/3r(1+0.4p2/3r)1/4[1+(Re282 000)5/8]4/5 (14) 2.4.2 比热容
大量试验证明,非牛顿流体的比热容随温度变化明显,常温条件下钻井液、水泥浆的比热容与高温条件下相比相差较大[25]。同时,比热容的改变也会对温度场产生影响。因此若准确模拟固井循环过程中的井筒温度场,必须考虑比热容与温度之间的相互影响。描述非牛顿流体比热容与温度关系的公式为:
ci=Aθ2+Bθ+C (15) 式中:i为钻井液、水泥浆或前置液;
ci 为第i种流体在温度θ 条件下的比热容,J/(kg·℃);A,B和C为回归系数。由于固井工艺涉及流体较多,现场应用时可根据需要对钻井液、水泥浆等流体的热物性参数进行实测,进行回归求出每种流体的回归系数A,B和C(见表1)。
表 1 不同类型流体比热容与温度关系式的回归系数Table 1. Regression coefficient of specific heat capacity variation with temperature for different types of fluid流体类型 回归系数 A B C 前置液 0.0227 19.985 0 2675.5 钻井液 0.0224 8.4234 2275.9 水泥浆 0.3242 −18.199 0 1824.6 2.5 初始条件和边界条件
2.5.1 初始条件
不同区域海水的温度受季节的影响不断发生变化,该变化对井筒的传热过程影响较大。为准确描述初始时刻的海水温度,采用下式进行计算:
θs={θsurf(200−z)+13.68z200z<200a2+a1−a21+ez−a0a3200⩽ (16) 式中:
a_{\text{0}}\text{=}-\text{130.137} ;a_{\text{1}}=39.398\;39 ;a_{\text{2}}=2.307\;13 ;a_{\text{3}}= 402.731\;77 ;\theta_{\text{surf}} 为海水表面温度,℃。设定初始时刻井筒内流体的温度与同深度海水和地层的温度相同,则其温度可以表示为:
{\left. {{\theta _{{\mathrm{ci}}}}} \right|_{t = 0}} = {\left. {{\theta _{\mathrm{c}}}} \right|_{t = 0}} = {\left. {{\theta _{\mathrm{a}}}} \right|_{t = 0}} = {\theta _{\mathrm{s}}} + G\Delta z (17) 式中:G为地温梯度,℃/100m。
2.5.2 边界条件
在入口处,流体温度可通过传感装置实时测量。
{\left. {{\theta _{{\mathrm{ci}}}}} \right|_{z = 0}} = {\theta _{{\mathrm{in}}}} (18) 式中:
{\theta _{{\mathrm{in}}}} 为入口处流体温度,℃。在井底处,套管内流体、套管壁、环空内流体温度相等。
{\left. {{\theta _{{\mathrm{ci}}}}} \right|_{z = h}} = {\left. {{\theta _{\mathrm{c}}}} \right|_{z = h}} = {\left. {{\theta _{\mathrm{a}}}} \right|_{z = h}} (19) 2.6 模型求解
采用全隐式差分格式对传热模型进行离散化处理,使用有限差分法进行迭代求解[26],计算流程如图4所示:1)输入井身结构参数、固井流体性能参数等数据;2)对数学模型进行离散,对物理模型进行网格划分;3)利用水泥浆注入阶段界面位置描述方程计算当前时刻环空固井流体的位置分布;4)根据上一时刻各个节点的温度
\theta_{i, j}^{(n-1)} ,计算当前时刻对流换热系数等热力学参数;5)根据基础参数、计算得到的热力学参数、固井流体位置等数据,计算当前时刻各个节点的温度\theta_{i, j}^{n} ;6)判断计算结果是否满足计算精度要求,即|\theta_{i,j}^{n} -\theta_{i,j}^{n-1} |<ε,否则返回步骤4),直至满足条件;7)判断当前时刻注入阶段是否结束,否则返回步骤3),直到注入阶段结束;8)计算结束,输出相关计算结果。3. 模型验证
由于深水固井水泥浆注入过程中无法安放井下温度测量装置,导致固井过程中无法实时测量井下温度,因此难以利用固井井下实测温度数据验证本文的模型。对此,采用前人研究中的数据对本文模型进行验证,并进行误差原因分析。
当水深较小或为0时,本文模型同样适用于浅水井或陆上井。A井为四川盆地的一口深井,完钻井深5 800 m,上一开次套管内径220.5 mm、下至井深3 708 m,下入套管外径177.8 mm、壁厚12.65 mm。工作液入口温度,工作液、岩石、管柱的物性参数详见文献[27]。
在钻井液循环和水泥浆注入阶段,A井实测的环空流体出口温度、文献[27]中模型计算的环空流体出口温度和本文模型计算的环空流体出口温度如图5所示。从图5可以看出,本文模型计算出的环空出口温度比文献[27]模型偏低,本文模型计算结果与实测结果的相对误差较文献[27]模型低。这表明本文模型预测结果的精度更高,尤其在注入阶段后期,更接近实测温度,这主要是因为本文模型考虑了不同类型流体热力学性能的差异。
B井为一口深水井,水深2 000 m,具体井身结构和流体性能参数详见文献[14]。由图6可知,本文模型与文献[14]模型相比趋势一致但预测温度整体较高,预测套管内流体温度在井底相差最大,为8.9 ℃;预测环空内流体温度在井口相差最大,为10.1 ℃。这主要是因为本文模型考虑了不同区域传热系数的差异和流体热力学参数随温度变化等因素,因此模型的准确度和适用性更高。
4. 影响因素分析
模拟井的基础参数:井深5 454 m,水深2 021 m,井眼直径215.9 mm,下入套管外径139.7 mm、内径124.3 mm,入口温度25 ℃,海水表面温度20 ℃,地温梯度2.4 ℃/100m。表2为固井工作液的基础参数。对于钻井液循环阶段,其温度场变化规律与钻井过程类似。因此,本节重点针对水泥浆注入阶段,研究不同因素对温度场的影响规律,包括钻井液循环周数(影响注入阶段初始温度剖面)、排量、水泥浆比热容和水泥浆密度。
表 2 固井工作液基础参数Table 2. Basic parameters of cementing fluid流体类型 体积/m3 密度/(kg·m−3) 排量(L·s−1) 隔离液 22.7 1 800 28.3 冲洗液 7.3 1 020 13.6 水泥浆 65.6 1 900 15.1 后置液 11.1 1 040 25.3 顶替液 30.5 1 000 10.1 4.1 钻井液循环周数
图7所示为利用本文模型预测的不同钻井液循环时刻套管内和环空内流体温度剖面。由图7可知,随着钻井液循环周数增多,套管内和环空内流体温度在钻井液循环0~1周时间内变化较大,循环1~4周时变化幅度逐渐降低,而在循环4周以后基本保持不变。这主要是因为循环前期井筒内流体与地层温度差异大,热交换速率较快;循环一段时间后两者温度场向热平衡方向发展,热交换速率逐渐降低;循环4周以后,两者温度场处于平衡状态,宏观表现为井筒温度场基本不再变化。
图8所示为井底循环温度随钻井液循环周数的变化情况。从图8可以看出,随着钻井液循环周数增加,井底循环温度逐渐降低,但钻井液循环4周以后井底循环温度降低幅度非常小。因此,为降低水泥浆注入对井底循环温度和整体循环温度的影响及防止水泥浆提前凝固,在注入水泥浆之前,钻井液通常会循环2~4周。
4.2 注入排量
设定钻井液循环3周,利用本文模型计算了不同排量条件下,冲洗液与水泥浆界面温度随界面位置变化的情况,结果如图9所示。从图9可以看出,随着界面位置增深,大排量注入时界面温度较小排量注入时高,但这一规律在泥线下方某一位置处(井深2 000~2 300 m)发生反转。这是因为排量越大,水泥浆流速越快,水泥浆与周围流体/固体的热交换越不充分。
这一规律与钻井过程相反,由于水泥浆在到达顶替位置后将不再继续注入流体,因此在水泥浆从井口注入,到水泥浆停止注入期间,注入排量越高,水泥浆与地层接触的时间越短。在海水区,水泥浆温度高于海水温度,水泥浆向海水传递热量,因此排量越大,海水对水泥浆的降温作用越弱,同一位置处水泥浆温度就越高。同理,在地层区,水泥浆温度低于地层温度,注入排量越高,地层对水泥浆的升温作用也越不明显。
4.3 水泥浆比热容
设定钻井液循环3周,所用水泥浆的比热容与温度呈正相关,即温度降低比热容降低、温度升高比热容升高。图10所示为不同水泥浆比热容条件下水泥浆温度随界面位置的变化。
从图10可以看出,考虑比热容随温度变化的情况时,初始比热容越高,海水区水泥浆温度的下降速率越低,地层区水泥浆温度的升高速率也越低,温度高低的转折点发生在泥线附近。这是由于在传热方程Q=cρVΔt中,当其他条件不变、交换相同的热量时,水泥浆比热容越大,温度的变化越小,即传热过程对其降温或升温的作用越不明显。同时,若在计算过程中不考虑比热容随温度的变化情况,则预测的井底循环温度会偏高2~4 ℃,这会增加缓凝剂用量,进而增大地层气窜风险。
4.4 水泥浆密度
设定钻井液循环3周,图11所示为不同水泥浆密度条件下,注入阶段结束时的井筒温度剖面(候凝阶段的初始温度剖面)。从图11可以看出:水泥浆从井口向井底流入过程中,对于突变点1以上井段,水泥浆密度越大流体温度越高,而突变点1以下井段呈现相反规律。这一现象可通过热力学方程进行解释,由传热方程Q=CρVΔt可知,当其他条件不变、水泥浆释放或吸收相同热量时,水泥浆密度越大,温度变化的幅度越小,最终的温度也越高或越低。水泥浆从井底向井口流入过程中,环空流体先后经历了吸热(井底到突变点2)、放热(突变点2到突变点3)、再吸热(突变点3到井口)的传热过程,因此水泥浆密度与温度的相关性由正相关变为负相关再变为正相关。这一变化规律同样可通过传热方程进行解释。
5. 结 论
1)注入水泥浆之前,钻井液应循环2~4周,以降低注入过程中循环时间的改变(临时停泵、改变排量等)对井底循环温度的影响。
2)注水泥浆阶段,注入排量越大,水泥浆流速越快,水泥浆与周围环境的热交换越不充分,海水和地层对水泥浆的降温或升温作用也越不明显。
3)若计算过程中不考虑比热容随温度的变化情况,则预测的井底循环温度会偏高2~4 ℃,这会增加缓凝剂用量,进而增大地层气窜风险。
4)注入水泥浆过程中,环空流体先后经历了吸热、放热、再吸热的传热过程,水泥浆密度与温度的相关性由正相关变为负相关再变为正相关。
-
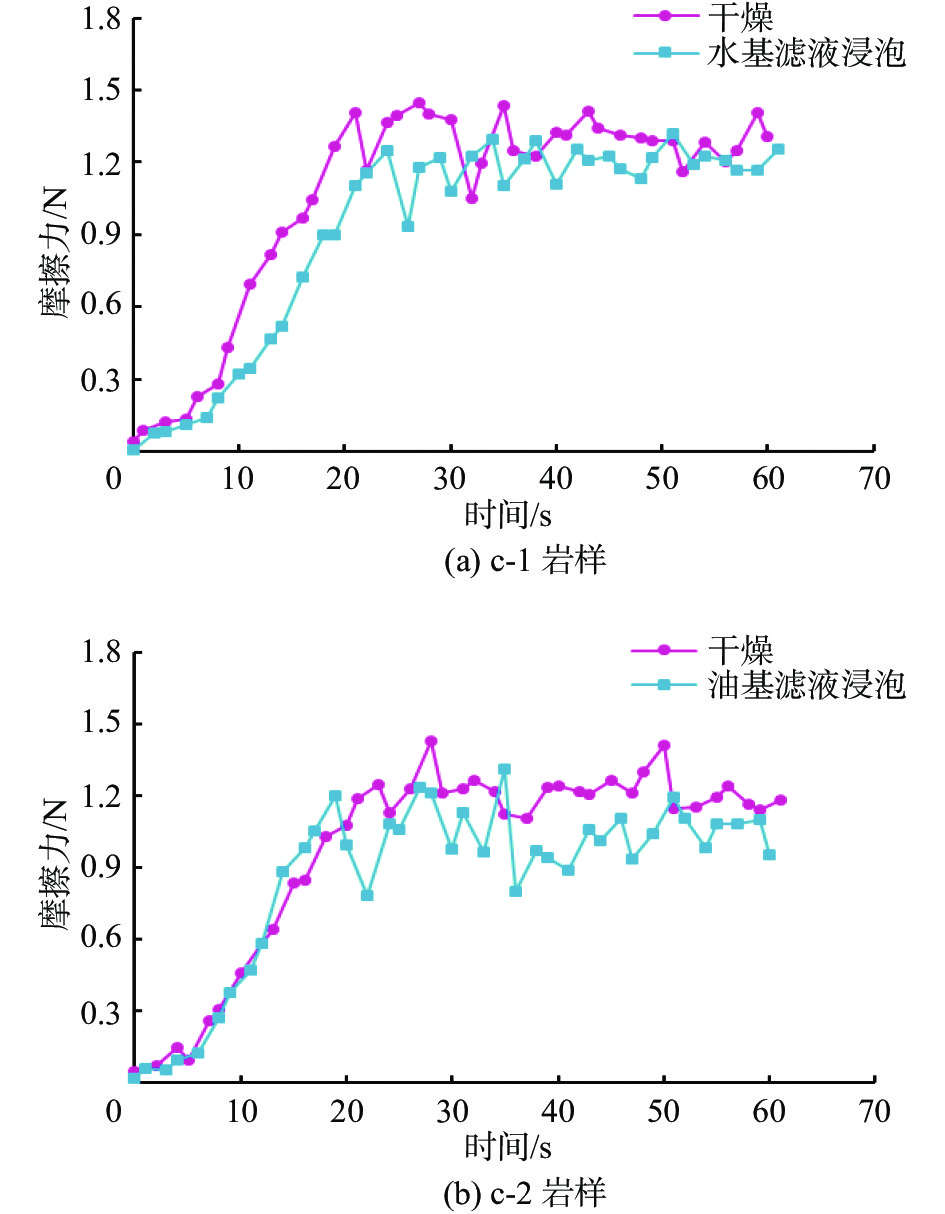
表 1 岩样不同环境下缝面摩擦因数测量结果
Table 1 Measurement results of friction factors of rock fracture surfaces under different situations
岩样
编号试验环境 浸泡流体 最大静摩擦
因数μ0动摩擦
因数μ1浸泡时
间/dC-1 干燥 0.63 0.58 0 滤液浸泡 水基钻井
液滤液0.55 0.53 3 C-2 干燥 0.60 0.59 0 滤液浸泡 油基钻井
液滤液0.55 0.48 3 -
[1] 臧艳彬,王瑞和,张锐. 川东北地区钻井漏失及堵漏措施现状分析[J]. 石油钻探技术,2011,39(2):60–64. doi: 10.3969/j.issn.1001-0890.2011.02.011 ZANG Yanbin, WANG Ruihe, ZHANG Rui. Current situation analysis of circulation lost and measures in Northeast Sichuan Basin[J]. Petroleum Drilling Techniques, 2011, 39(2): 60–64. doi: 10.3969/j.issn.1001-0890.2011.02.011
[2] KANG Yili, YOU Lijun, XU Xinghua, et al. Prevention of formation damage induced by mud lost in deep fractured tight gas reservoir in Western Sichuan Basin[J]. Journal of Canadian Petroleum Technology, 2012, 51(1): 46–51. doi: 10.2118/131323-PA
[3] 张杜杰,金军斌,陈瑜,等. 深部裂缝性致密储层随钻堵漏材料补充时机研究[J]. 特种油气藏,2020,27(6):158–164. HANG Dujie, JIN Junbin, CHEN Yu, et al. Study on the supplement timing of leakage stoppage materials while drilling for deep fractured tight reservoirs[J]. Special Oil & Gas Reservoirs, 2020, 27(6): 158–164.
[4] 王建云,杨晓波,王鹏,等. 顺北碳酸盐岩裂缝性气藏安全钻井关键技术[J]. 石油钻探技术,2020,48(3):8–15. WANG Jianyun, YANG Xiaobo, WANG Peng, et al. Technologies for the safe drilling of fractured carbonate gas reservoirs in the Shunbei Oil and Gas Field[J]. Petroleum Drilling Techniques, 2020, 48(3): 8–15.
[5] 周志世,张震,张欢庆,等. 长裸眼多层系砂泥岩互层井底断层洞穴裂缝失返井漏桥接堵漏工艺技术[J]. 钻井液与完井液,2020,37(4):456–464. ZHOU Zhishi, ZHANG Zhen, ZHANG Huanqing, et al. Controlling mud losses into caves with bridging techniques in ultra-deep long open hole[J]. Drilling Fluid & Completion Fluid, 2020, 37(4): 456–464.
[6] 李冬梅,柳志翔,李林涛,等. 顺北超深断溶体油气藏完井技术[J]. 石油钻采工艺,2020,42(5):600–605. LI Dongmei, LIU Zhixiang, LI Lintao, et al. Well completion technologies for the ultra-deep fault-dissolved oil and gas reservoir in Shunbei Oil and Gas Field[J]. Oil Drilling & Production Technology, 2020, 42(5): 600–605.
[7] 王维斌,马廷虎,邓团. 川东宣汉–开江地区恶性井漏特征及地质因素[J]. 天然气工业,2005,25(2):90–92. doi: 10.3321/j.issn:1000-0976.2005.02.029 WANG Weibin, MA Tinghu, DENG Tuan. Characteristics and geological factors of vicious lost circulation in Xuanhan-Kaijiang Area of East Sichuan[J]. Natural Gas Industry, 2005, 25(2): 90–92. doi: 10.3321/j.issn:1000-0976.2005.02.029
[8] 杨振杰. 国外礁灰岩漏失地层钻井技术[J]. 钻井液与完井液,2004,21(1):45–49. doi: 10.3969/j.issn.1001-5620.2004.01.014 YANG Zhenjie. Drilling technology for biolithite loss zone abroad[J]. Drilling Fluid & Completion Fluid, 2004, 21(1): 45–49. doi: 10.3969/j.issn.1001-5620.2004.01.014
[9] MAURY V, GUENOT A. Practical advantages of mud cooling systems for drilling[J]. SPE Drilling & Completion, 1995, 10(1): 42-48.
[10] YAN Wei, GE Hongkui, WANG Jianbo, et al. Experimental study of the friction properties and compressive shear failure behaviors of gas shale under the influence of fluids[J]. Journal of Natural Gas Science and Engineering, 2016, 33: 153–161. doi: 10.1016/j.jngse.2016.04.019
[11] 邹雨时,张士诚,马新仿. 页岩压裂剪切裂缝形成条件及其导流能力研究[J]. 科学技术与工程,2013,13(18):5152–5157. doi: 10.3969/j.issn.1671-1815.2013.18.013 ZOU Yushi, ZHANG Shicheng, MA Xinfang. Research on the formation conditions and conductivity of shear fracture for hydraulic fracturing in gas-shale[J]. Science Technology and Engineering, 2013, 13(18): 5152–5157. doi: 10.3969/j.issn.1671-1815.2013.18.013
[12] FREDD C N, MCCONNELL S B, BONEY C L, et al. Experimental study of fracture conductivity for water-fracturing and conventional fracturing applications[J]. SPE Journal, 2001, 6(3): 288–298. doi: 10.2118/74138-PA
[13] YAN Xiaopeng, YOU Lijun, KANG Yili, et al. Impact of drilling fluids on friction coefficient of brittle gas shale[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 106: 144–152. doi: 10.1016/j.ijrmms.2018.04.026
[14] YOU Lijun, KANG Yili, CHEN Zhangxin, et al. Wellbore instability in shale gas wells drilled by oil-based fluids[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 72: 294–299. doi: 10.1016/j.ijrmms.2014.08.017
[15] 康毅力,佘继平,林冲,等. 钻井完井液浸泡弱化页岩脆性机制[J]. 力学学报,2016,48(3):730–738. doi: 10.6052/0459-1879-15-286 KANG Yili, SHE Jiping, LIN Chong, et al. Brittleness weakening mechanisms of shale soaked by drilling & completion fluid[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3): 730–738. doi: 10.6052/0459-1879-15-286
[16] 康毅力, 游利军, 李大奇, 等. 高温高压钻井液漏失动态评价仪: CN201210023152.4[P]. 2012-02-02. KANG Yili, YOU Lijun, LI Daqi, et al. High temperature and high pressure drilling fluid leakage dynamic evaluation instrument: CN201210023152.4[P]. 2012-02-02.
[17] 陈平,韩强,马天寿,等. 基于微米压痕实验研究页岩力学特性[J]. 石油勘探与开发,2015,42(5):662–670. CHEN Ping, HAN Qiang, MA Tianshou, et al. The mechanical properties of shale based on micro-indentation test[J]. Petroleum Exploration and Development, 2015, 42(5): 662–670.
[18] CHAN A W, HAUSER M, COUZENS-SCHULTZ B A, et al. An alternative interpretation of leakoff and lost circulation pressure measurements[R]. ARMA-2013-302, 2013.
[19] COUZENS-SCHULTZ B A, CHAN A W. Stress determination in active thrust belts: an alternative leak-off pressure interpretation[J]. Journal of Structural Geology, 2010, 32(8): 1061–1069. doi: 10.1016/j.jsg.2010.06.013
[20] 黄元敏,马胜利,杨马陵. 不同岩性下水对断层摩擦性状影响的实验研究[J]. 地震,2015,35(4):21–29. doi: 10.3969/j.issn.1000-3274.2015.04.003 HUANG Yuanmin, MA Shengli, YANG Maling. Experimental study of water effect on frictional characteristics for different lithology[J]. Earthquake, 2015, 35(4): 21–29. doi: 10.3969/j.issn.1000-3274.2015.04.003
[21] 韩秀玲,杨贤友,熊春明,等. 超深裂缝性厚层改造效果影响因素分析与高效改造对策[J]. 天然气地球科学,2017,28(8):1280–1286. HAN Xiuling, YANG Xianyou, XIONG Chunming, et al. Influencing factors and efficient reservoir stimulation countermeasuresin thick and ultra-deep naturally fractured reservoir[J]. Natural Gas Geoscience, 2017, 28(8): 1280–1286.
[22] 陈颙, 黄庭芳, 刘恩儒. 岩石物理学[M]. 合肥: 中国科学技术大学出版社, 2009: 172–182. CHEN Yong, HUANG Tingfang, LIU Enru. Rock physics[M]. Hefei: University of Science and Technology of China Press, 2009: 172–182.
[23] ZHANG Huijie, LIU Shuhai, XIAO Huaping. Frictional behavior of sliding shale rock-silica contacts under guar gum aqueous solution lubrication in hydraulic fracturing[J]. Tribology International, 2018, 120: 159–165. doi: 10.1016/j.triboint.2017.12.044
[24] 高文龙,姜耀东,湛川. 软弱结构面表面形态与充填度的力学特性研究[J]. 工程地质学报,2010,18(1):127–131. doi: 10.3969/j.issn.1004-9665.2010.01.019 GAO Wenlong, JIANG Yaodong, ZHAN Chuan. The study of structural-plane based on appearance and backfilling state[J]. Journal of Engineering Geology, 2010, 18(1): 127–131. doi: 10.3969/j.issn.1004-9665.2010.01.019
[25] 雷国辉, 陈晶晶. 有效应力决定饱和岩土材料抗剪强度的摩擦学解释[J]. 岩土工程学报, 2011, 33(10): 1517-1525. LEI Guohui, CHEN Jingjing. Tribological explanation of effective stress controlling shear strength of saturated geomaterials[J]. Chi-nese Journal of Geotechnical Engineering, 2011, 33(10): 1517-1525.
[26] 曾义金,李大奇,杨春和. 裂缝性地层防漏堵漏力学机制研究[J]. 岩石力学与工程学报,2016,35(10):2054–2061. ZENG Yijin, LI Daqi, YANG Chunhe. Leakage prevention and control in fractured formations[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(10): 2054–2061.
[27] 俞杨烽. 富有机质页岩多尺度结构描述及失稳机理[D]. 成都: 西南石油大学, 2013: 61–80. YU Yangfeng. Multi-scale structure description and borehole instability mechanism of organic rich shale[D]. Chengdu: Southwest Petroleum University, 2013: 61–80.
[28] 李鹏,刘建,李国和,等. 水化学作用对砂岩抗剪强度特性影响效应研究[J]. 岩土力学,2011,32(2):380–386. doi: 10.3969/j.issn.1000-7598.2011.02.010 LI Peng, LIU Jian, LI Guohe, et al. Experimental study for shear strength characteristics of sandstone under water-rock interaction effects[J]. Rock and Soil Mechanics, 2011, 32(2): 380–386. doi: 10.3969/j.issn.1000-7598.2011.02.010
[29] WITHERSPOON P A, WANG J S Y, IWAI K, et al. Validity of cubic law for fluid flow in a deformable rock fracture[J]. Water Resources Research, 1980, 16(6): 1016–1024. doi: 10.1029/WR016i006p01016
[30] 王剑波. 页岩储层缝面摩擦滑动特性研究[D]. 北京: 中国石油大学(北京), 2016: 61-62. WANG Jianbo. Study on frictional sliding characteristics of fracture surface of shale reservoir[D]. Beijing: China University of Petroleum(Beijing), 2016: 61-62.
-
期刊类型引用(3)
1. 刘金璐,李军,柳贡慧,李宁,张权,周宝,孙红宇. 控压固井分段降密度环节井筒温压场预测模型研究. 石油科学通报. 2025(01): 107-119 .  百度学术
百度学术
2. 朱雷,潘金林,陈雪莲,马锐,田隆梅,周浩栋. 套管和水泥环尺寸对CBL/VDL测井套管波的影响研究. 石油钻探技术. 2025(01): 136-143 .  本站查看
本站查看
3. 戴亚,茆长杨,王康兴,徐子锋. 散粮带式输送机温度监控系统的设计及应用. 现代食品. 2024(18): 15-19+23 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载: