南海莺–琼盆地多为存在高温高压的复杂地层，在钻达目的层前要钻穿多套不同压力、不同岩性的地层，且常常面临钻井液安全密度窗口窄的问题。起下钻、下套管、注水泥等作业时会产生压力波动，导致井底和环空压力发生变化，容易诱发井漏、井塌、溢流甚至井喷等井下故障。其中，在钻井液安全密度窗口窄的井段下套管和注水泥作业时，若套管与井眼之间的间隙过小或下套管速度过快，会产生过大的压力波动，引起井漏等井下故障，严重影响钻井的顺利进行。因此，套管–井眼间隙以及下套管施工参数是影响下套管和注水泥作业安全的主要因素。目前南海莺–琼盆地多采用根据钻井经验得出的井身结构，对于套管–井眼间隙是否合理缺乏一定的理论研究。因此笔者以波动压力为指标对莺–琼盆地套管–井眼间隙进行优化。

关于波动压力的计算，已经有很多学者进行了研究^[1–10]，形成的计算方法主要有以Burkhardt为代表的稳态计算方法和以Lubinski为代表的瞬态计算方法。已有文献表明：对于浅井，稳态计算方法和瞬态计算方法的计算结果与实测结果均较为接近；对于深井，实测结果与瞬态计算方法的计算结果较为接近，而稳态计算方法的计算结果要比实测结果大50%～100%^[10]。由于莺–琼盆地压力台阶多，钻井液安全密度窗口窄，且所钻井大都是深井、超深井，因此笔者选用更为精确的瞬态计算方法，结合南海莺–琼盆地钻井情况，通过建立下套管过程中井筒内抽汲和激动压力的计算模型，分析不同直径井眼和套管配合条件下井筒内波动压力的变化规律，优化出南海莺–琼盆地套管–井眼间隙，为南海莺–琼盆地高温高压窄安全密度窗口复杂地层井身结构设计提供参考。

1.   瞬态波动压力计算模型

在充有钻井液的井眼内下套管时，套管带动钻井液流动，使井筒内钻井液的流速剧烈变化，从而引起压力发生大幅度波动，形成水击现象。出现水击现象的原因是液体具有惯性和压缩性。液体的惯性企图维持液体的原有运动状态，所以流速的改变会导致压力剧烈变化。水击现象是造成下套管时产生波动压力的主要原因。在充有钻井液的井眼内下入套管的过程中，考虑到套管运行速度随时间的变化以及井壁、套管柱的弹性和钻井液的压缩性，此时对钻井液流动造成的影响必然是瞬时的。因此，可以利用在弹性管一维可压缩流体理论上建立的一维不稳定流动方程，分析井内的瞬态波动压力。

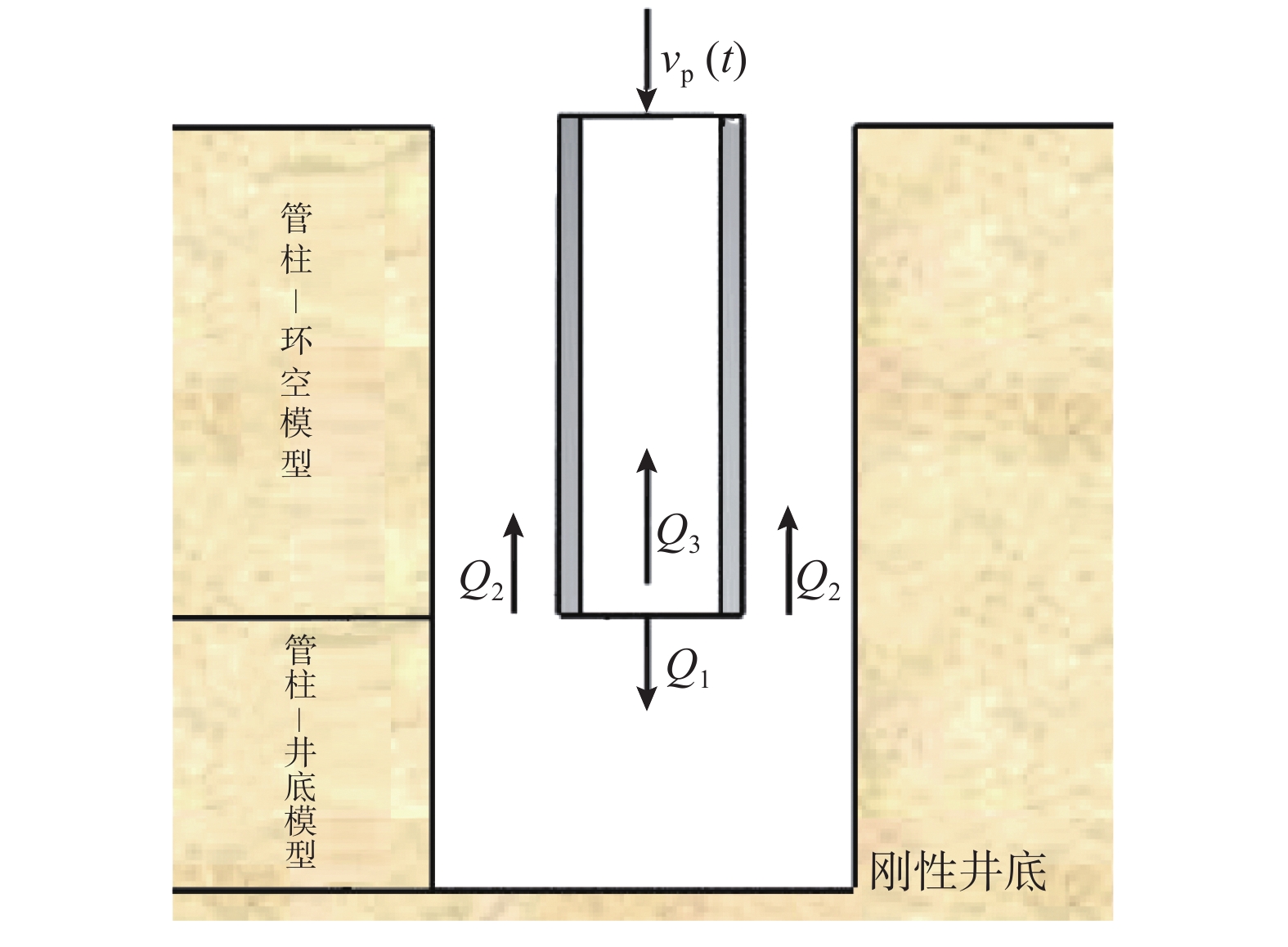
图1为井眼内水力系统的基本水力学模型。图1中：Q₁为下套管过程中套管柱以下井眼内钻井液的流量，m³/s；Q₂为套管与井眼环空内钻井液的流量，m³/s；Q₃为套管内钻井液的流量，m³/s；v_p（t）为套管下入速度，m/s；在井口应用地面边界条件，在套管柱末端应用力和顶替相容边界条件。

该模型为瞬态波动压力预测模型，由套管–环空模型和套管–井底模型组成，具有以下特征：1）地层、套管和井眼为弹性体，井底为刚性体；2）套管的轴向弹性和流体黏滞力决定套管替出流体的量；3）流体性能是温度和压力的函数；4）井口与大气连通。

该井内力学模型所代表的井内水力流动系统由环空流道（从套管底端到井口）、套管内圆管流道（从套管底端到井口）和圆形流道（从套管底端到井底）组成。

水击运动的基本方程组为^[11–12]：

将式（1）应用到下套管过程，根据图1井内水力模型对其进行变形，可得一维不稳定流动的基本方程：

图  1  下套管时井内水力模型

Figure  1.  Hydraulic model during casing running

下载: 全尺寸图片 幻灯片

式中：v为流体速度，m/s；s为流体段长，m；ρ为流体密度，kg/m³；p为波动压力，Pa；t为时间，s；z为轴向坐标，m；γ为流体重度，N/m³；g为重力加速度， m/s²；Q为钻井液流量，m³/s；A为流道的横截面积，m²；p_f为摩擦阻力（是Q，v_P等的函数），N；v_p为套管下入速度（是时间的函数），m/s；C为压力传播速度（与流体密度、钻井液压缩系数和流道膨胀系数有关），m/s。

采用特征线法^[12–14]求解式（2），初始条件和边界条件按开口管关泵或堵口管关泵确定。基于式（2）编制瞬态波动压力计算软件，输入参数为井身结构、钻井液密度、钻井液流性指数和稠度系数，套管下入的速度及加速度；输出结果为井底最大波动压力随时间的变化曲线及波动压力最大时刻波动压力随井深的变化曲线。

2.   套管与井眼合理间隙的确定

2.1   南海莺–琼盆地常用井身结构

目前南海莺–琼盆地最常用的5层套管层序为ϕ762.0 mm隔水管+ϕ508.0 mm表层套管+ϕ339.7 mm技术套管+ϕ244.5 mm技术套管+ϕ177.8 mm尾管。以LD10–2–x井为例，其井身结构为：一开，ϕ914.4 mm钻头钻至井深205.00 m，ϕ762.0 mm隔水管下至井深200.00 m；二开，ϕ660.4 mm钻头钻至井深1 263.00 m，ϕ508.0 mm套管下至井深1 258.00 m；三开，ϕ444.5 mm钻头钻至井深3 356.00 m，ϕ339.7 mm套管下至井深3 351.00 m；四开，ϕ311.1 mm钻头钻至井深4 028.00 m，ϕ244.5 mm套管下至井深4 023.00 m；五开，ϕ212.7 mm钻头钻至井深4 195.00 m，ϕ177.8 mm尾管下至井深4 190.00 m。

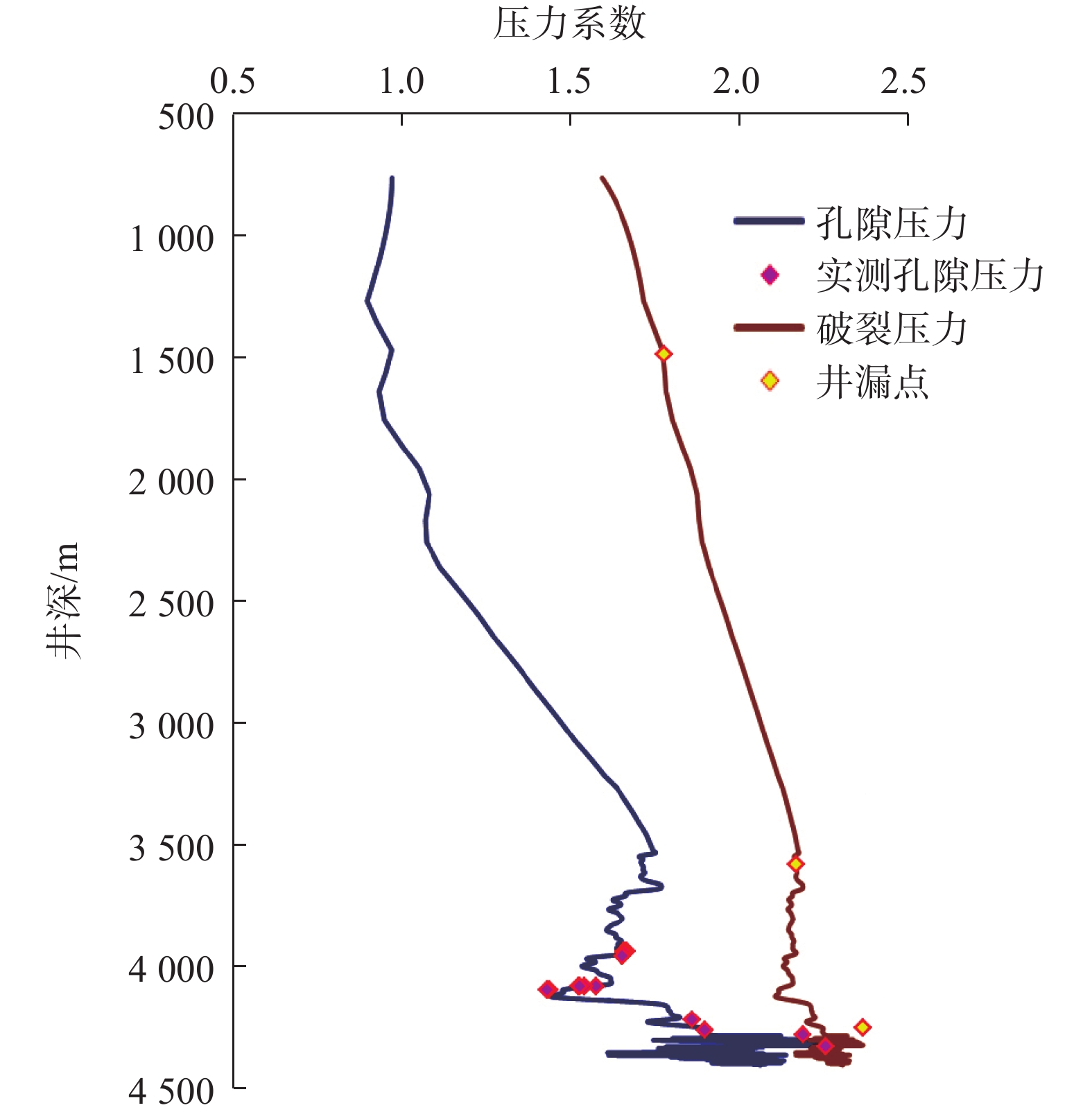
以南海莺–琼盆地LD10–2–x井为分析对象，根据该井不同井深下的地层破裂压力当量密度和地层孔隙压力当量密度绘制地层压力剖面，结果如图2所示。

图  2  南海莺–琼盆地LD10–2–x井地层压力剖面

Figure  2.  Formation pressure profile of Well LD10-2-x in the Ying-Qiong Basin of the South China Sea

下载: 全尺寸图片 幻灯片

由图2可知，该井井深约4 200.00 m处的安全密度窗口较窄。安全密度窗口窄是指由于地层孔隙压力、破裂压力和坍塌压力决定的安全钻井作业当量钻井液密度范围，不能按常规钻井进行正常密度附加。如果当量钻井液密度超出此范围则造成井漏，低于此范围则易造成井涌。

南海莺–琼盆地储层具有压力和温度高、钻井液安全密度窗口窄的特点，钻井液安全密度窗口在0.10 kg/L左右；钻井所用钻井液黏度高、切力和流动摩阻大。这些因素导致油气井在下套管时产生的波动压力较大，采用常规的套管–井眼间隙极易发生井漏。所以南海莺–琼盆地受窄安全密度窗口影响易发生气窜或漏失等井下故障，且存在滤饼清洗困难的问题。在确定合理套管–井眼间隙时，必须在窄安全密度窗口条件下计算相应的波动压力，以避免发生固井事故。笔者将分析该井五开井段，即窄安全密度窗口处（井深4 200.00 m）井筒内的压力当量密度，并确定合理的套管–井眼间隙。

2.2   波动压力随时间的变化规律

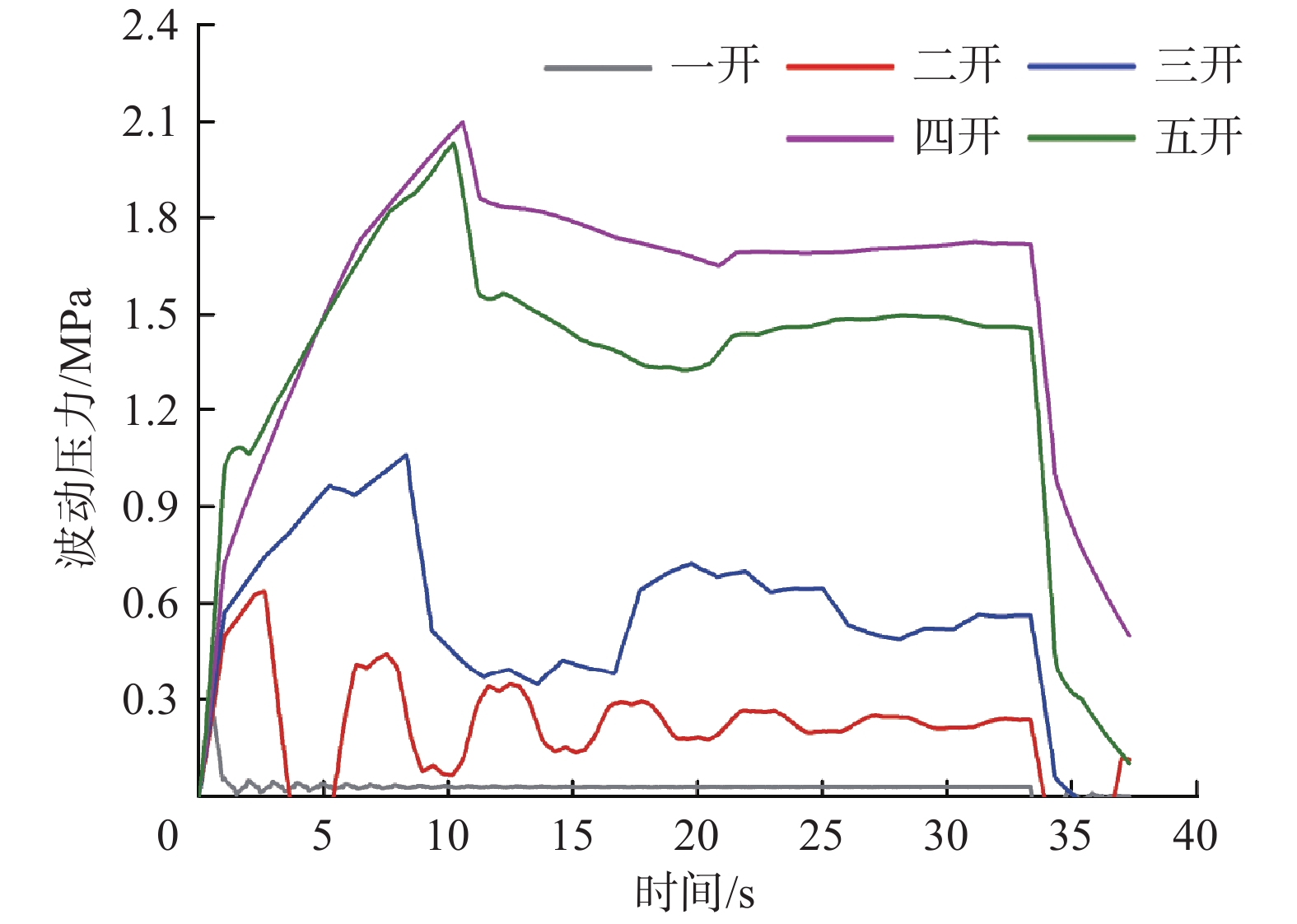
根据上文建立的瞬态波动压力计算模型编制波动压力计算软件，以LD10–2–x井为研究目标，模拟下入最后一根套管过程中井底波动压力的变化，并以此计算各开次的波动压力，结果见图3。模拟计算条件：井身结构如前所述；钻井液的流变模式为幂律模式；套管状态为开口管关泵；套管最大下入速度为18.00 m/min，加速度为0.30 m/s²，套管下入时先匀加速再匀速最后匀减速；单根套管长度为11.00 m；尾管使用ϕ139.7 mm钻杆下至井底。

图  3  LD10–2–x井各开次井底波动压力随时间的变化曲线

Figure  3.  The variation of bottom hole surge pressure vs. time in Well LD10-2-x

下载: 全尺寸图片 幻灯片

由图3可以看出：随时间增长，各开次波动压力先升高，当套管均加速下入结束时，产生第一波峰，同时也是最高波峰，此时井底波动压力达到最大，随后波动压力呈现周期性衰减，并随着套管下入速度降低而降至0；同时，随开次增加，波动压力整体呈升高趋势，但五开井段的波动压力整体小于四开井段，原因是五开井段套管为尾管，使用小尺寸钻杆送入，因此上部钻杆与井眼的间隙较大，造成波动压力降低；五开井底最大波动压力为1.98 MPa。以上结果与现场钻井实践基本一致，进一步说明了本文所用方法的可靠性。

2.3   最大波动压力随套管–井眼间隙变化的规律

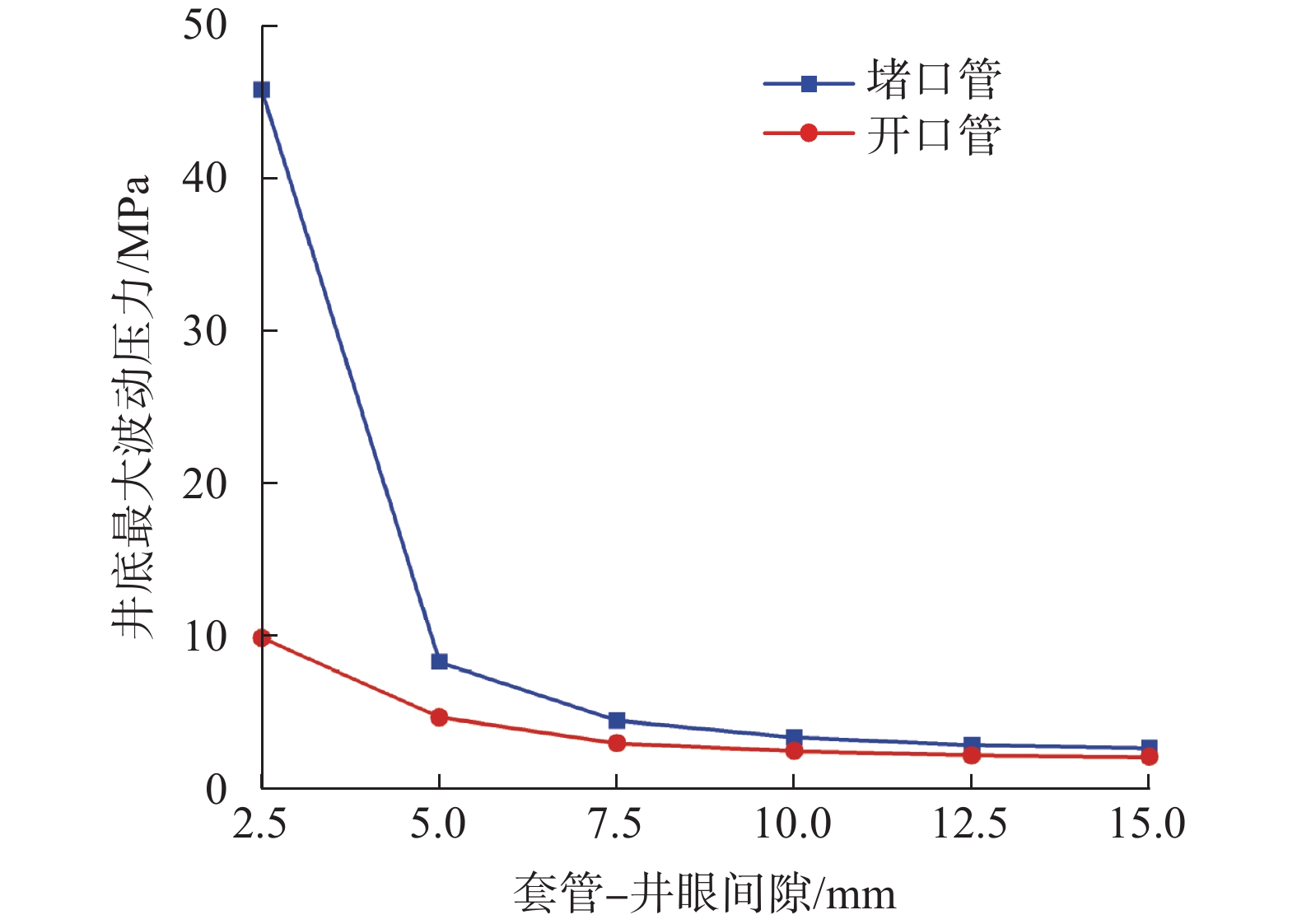
由于在下套管过程中钻井泵处于关泵状态，所以井筒内的压力由钻井液产生的静液柱压力和波动压力2部分组成。下套管过程中必须要满足井筒内的压力大于地层孔隙压力，小于地层破裂压力。由图2可以看出，LD10–2–x井在井深4 200.00 m左右的钻井液安全密度窗口约为0.10 kg/L。为研究窄安全密度窗口处，即五开井底处的波动压力随套管–井眼间隙变化的规律，将尾管直径固定为177.8 mm，通过改变井眼尺寸来调整套管–井眼间隙，进而计算不同间隙下的最大井底波动压力，计算条件为开口管关泵和堵口管关泵，其他模拟条件与上述相同。

图4为LD10–2–x井五开井底最大波动压力随套管–井眼间隙变化的规律。由图4可以看出，随套管–井眼间隙增大，井底最大波动压力逐渐降低，且降低幅度也逐渐减小。窄安全密度窗口处（即井深4 195.00 m处）的钻井液安全密度窗口为0.10 kg/L，故在保证下套管过程中不会发生因井内压力波动造成地层破裂的前提下，计算出井底最大波动压力不得超过4.1 MPa。根据该波动压力值，从图4可以得到：在开口管情况下，套管–井眼间隙不得小于5.70 mm；在堵口管情况下，套管–井眼间隙不得小于8.45 mm。

图  4  LD10–2–x井五开井底最大波动压力随套管–井眼间隙变化的规律

Figure  4.  The variation of the maximum bottom hole surge pressure vs. casing-wellbore gap during the fifth spud in Well LD10-2-x

下载: 全尺寸图片 幻灯片

2.4   注水泥过程中井底最大当量循环密度随套管–井眼间隙变化的规律

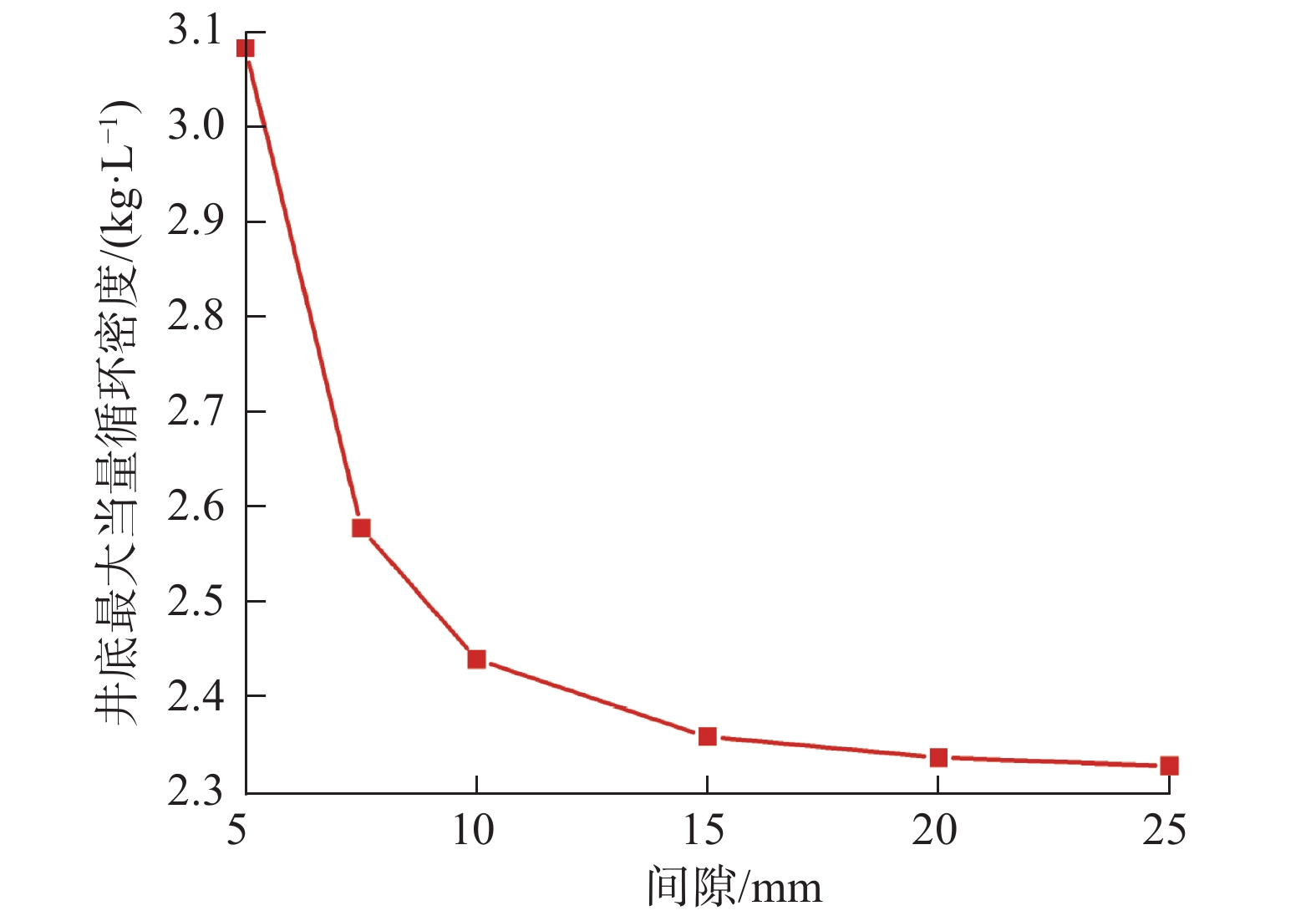
由于套管–井眼间隙不仅影响下套管过程中的波动压力，同时也会对注水泥过程中的井底压力产生影响，为了保证地层不被压漏，还需考虑注水泥过程中井底最大当量循环密度的影响。使用Landmark软件计算LD10–2–x井五开注水泥过程中井底当量循环密度与套管–井眼间隙的关系，结果见图5。模拟计算条件：钻井液密度2.26 kg/L，流性指数0.71，稠度系数0.286 2 Pa·sⁿ；隔离液密度2.30 kg/L，流性指数0.82，稠度系数0.492 8 Pa·sⁿ；水泥浆密度2.397 kg/L，流性指数0.87，稠度系数0.651 5 Pa·sⁿ，造浆率1.441 m³/t，混合水0.976 9 m³/t；注替参数按照现场实际施工参数输入。

由图5可以看出，随着套管–井眼间隙增大，井底最大当量循环密度逐渐降低，且降低幅度也逐渐减小。窄安全密度窗口处的钻井液密度窗口为0.10 kg/L，故在保证注水泥过程中不会发生因井内压力造成地层破裂的前提下，计算出井底最大当量循环密度不得超过2.36 kg/L。根据该密度值，从图5可以得到，套管–井眼间隙不得小于15.0 mm。

图  5  LD10–2–x井五开注水泥过程中井底最大当量循环密度与套管–井眼间隙的关系

Figure  5.  Relationship between the maximum bottom hole ECD and the casing-wellbore gap during the cementing of the fifth spud section in Well LD10-2-x

下载: 全尺寸图片 幻灯片

综上所述，对于LD10–2–x井，由下套管过程中井底波动压力确定的最小套管–井眼间隙为5.70 mm（开口管）和8.45 mm（堵口管）；由注水泥过程中井底最大当量循环密度确定的最小套管–井眼间隙为15.00 mm；若保持前一开次井身结构不变，由几何尺寸限定的最大井眼间隙为19.55 mm，因此，合理的套管–井眼间隙为15.00～19.55 mm。LD10–2–x井五开实际套管–井眼间隙为17.45 mm，在合理的套管–井眼间隙范围内。LD10–2–x井五开尾管固井作业顺利，未出现井漏等井下故障，证明了上文计算方法计算结果的合理性。

3.   结　论

1）通过建立下套管过程中的瞬态波动压力计算模型，并与注水泥过程中的当量循环密度分析结果相结合，可以确定不同井深处合理的套管–井眼间隙。

2）对于LD10–2–x井，计算出的窄安全密度窗口处合理的套管–井眼间隙为15.00～19.55 mm，该井窄安全密度窗口处实际套管–井眼间隙为17.45 mm，固井施工作业顺利，证明采用文中方法确定的套管–井眼间隙合理。

3）若要进一步确定更加合理的套管–井眼间隙，需分析各开次套管鞋处的波动压力和注水泥过程中的当量循环密度，取其交集作为合理的套管–井眼间隙。