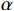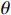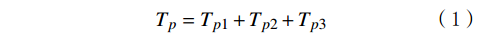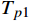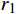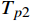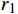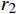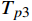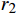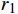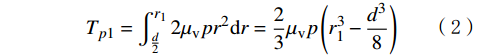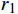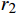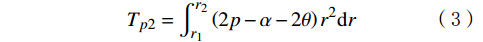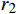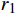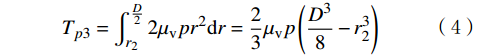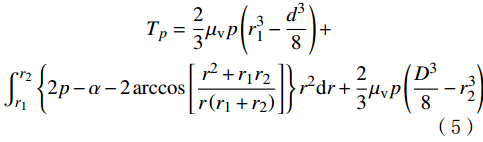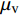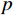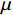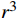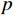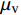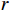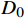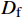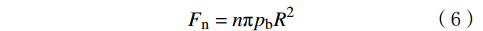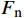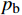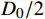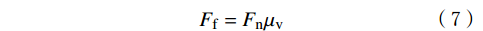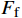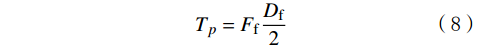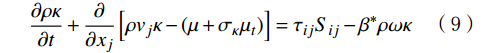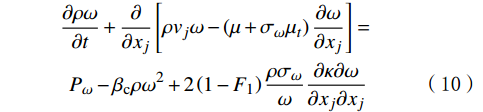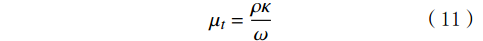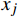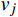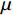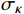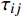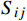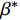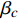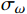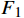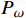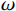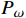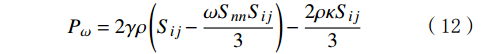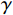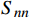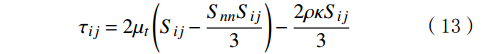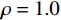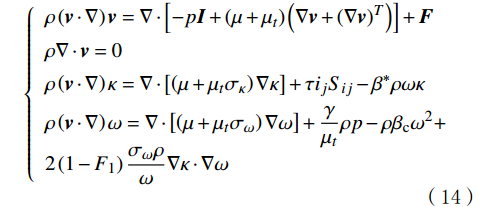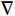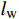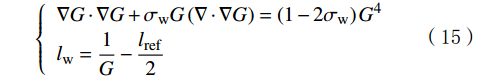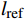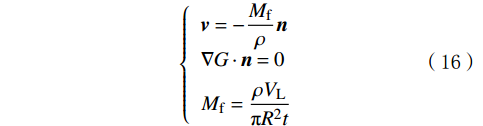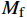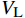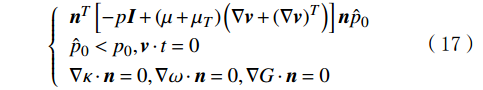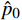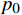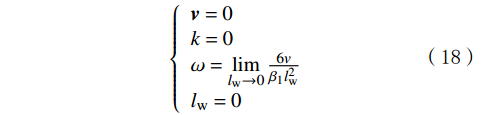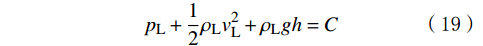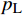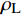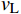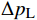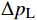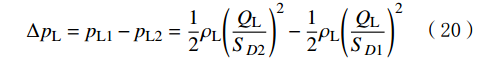Design of Dynamic and Static Disc Valves in Static Thrust-Type Mechanical Vertical Drilling Tool and Clearance Flow Analysis
-
摘要:
为解决深井、超深井等钻井过程中复杂工况下防斜打直的技术难点,提出了可在高温、强振条件下经济、安全、可靠使用的静态推靠机械式垂钻工具的研制思路,计算了其关键组件动静盘阀组的摩阻力,采用有限元法分析了环阀间隙的流动,基于井眼高低边快速关断响应规律设计了环形阀的结构及流道,并使用全尺寸试验台架开展了ϕ177.8 mm静态推靠机械式垂钻工具地面水力台架试验。研究表明:为减小盘阀摩擦面积,将其设计为2层组合,上部设计异形孔和凸台,下部设计异形结构的旁流道;采用硬质合金材料整体成型技术,上下盘阀间隙控制在0.5 mm,上下盘阀凸台高度均控制在0.25 mm;地面台架试验结果表明,动静盘阀组导向分流正常,密封保压性能指标达到了预期设计要求。研究结果可为静态推靠机械式垂钻工具结构的设计优化提供依据。
Abstract:To solve the technical problem of anti-oblique drilling in the complex working conditions of deep wells and ultra-deep wells, the idea of developing a static thrust-type mechanical vertical drilling tool that can be used economically, safely, and reliably under the condition of high temperature and strong vibration was proposed. The friction resistance of the key components of the dynamic and static disc valve group was calculated, and the finite element analysis of the clearance flow of the ring valve was carried out. The ring valve structure and flow channel were designed based on the rapid shut-off response law of the high and low sides of the well, and the ground hydraulic bench test of the ϕ177.8 mm static thrust-type mechanical vertical drilling tool was carried out using the full size test bench. The results show that to reduce the friction area of the disc valve, a combination of two layers is recommended. The upper part is designed with a special-shaped hole and boss, and the lower part is designed with a special-shaped bypass. The hard alloy material is used for integral molding. The clearance between the upper and lower disc valves is controlled at 0.5 mm, and the height of the boss of the upper and lower disc valves is controlled at 0.25 mm. Through the ground bench test, it is proved that the dynamic and static disc valve group can direct and shunt the water flow normally. The performance index of sealing and pressure-holding has reached the expected design requirements. The results can provide a reference for structural design optimization of static thrust-type mechanical vertical drilling tools.
-
Keywords:
- static thrust /
- mechanical /
- vertical drilling tool /
- disc valve /
- structural design /
- clearance flow /
- horizontal bench test
-
对于高陡构造、大倾角等易斜地层的防斜打快,依靠常规钻直井的井斜控制技术已不能满足要求[1–3],迫切需要适用于高转速、可靠性高及能耐高温强振的低成本垂直钻井工具[4–5]。自德国大陆深钻计划项目(kontinentales tiefborh programm der bundesrepublik deutschland,KTB)主孔(井深9 101 m)成功应用自动垂直钻井系统(VDS)以来,相继研发了贝克休斯公司的VertiTrak、斯伦贝谢公司的Power V等垂直钻井系统[6–7]。但这些垂直钻井系统的机电液系统对井下高温(高于150 ℃)、强振动等复杂条件的适应性差、可靠性低[8–9]。因此,近年来经济、安全、可靠的纯机械式自动垂直钻井系统逐渐受到关注,尤其在低油价的经济形势下,成为防斜打快钻井的最佳选择。
静态推靠机械式垂钻工具通过偏重块与动静盘阀组的相互作用实现井下实时闭环式主动防斜、纠斜,动静盘阀组作为该类垂钻工具的重要核心部件之一,决定着其能否保证井下实现垂直钻进[10–12]。摩阻决定着其分流导流效果,动静盘阀间缝隙决定着其密封效果,设计是否合理也是影响静态推靠机械式垂钻工具整体可靠性的关键因素之一。目前,国外类似结构大都采用电机驱动的方式实现动静阀组的可控关断,与偏重驱动方式存在机理上的不同。因此,笔者计算了动静盘阀组的摩阻力,采用有限元法分析了环阀间隙的流动规律,基于井眼高低边快速关断响应规律设计了环形阀的结构及流道,并进行了地面台架试验,以期研制出适用于高温、强振条件,经济、安全、可靠的静态推靠机械式垂钻工具。
1. 静态推靠机械式垂钻工具研制思路
1.1 工具结构
拟研制的静态推靠垂钻工具为纯机械式结构[13–15],由重力偏重稳定平台、双层推靠机构、动力芯轴及PDC复合轴承等部件组成(如图1所示),具有3层独立旋转系统,能够在钻井过程中实现主动防斜纠斜,是井下闭环钻井工具[16–18]。
静态推靠机械式垂钻工具通过重力偏重稳定平台动态响应井斜角变化,响应精度要达到1°。动力芯轴传递钻压扭矩,隔离钻头破岩产生的振动冲击。经过滤的小排量高压钻井液可以净化轴承,为推靠机构提供动力源。安装在近钻头的双层静态推靠机构,利用钻头水力压差实现准静态推靠井壁,推靠力要达到10 kN以上。静态推靠机械式垂钻工具的基本结构如图2所示。
1.2 工作原理
静态推靠机械式垂钻工具主要用于解决直井段钻井时的防斜打直问题。实际钻进中,工具下端连接钻头,上端连常规钻具和螺杆钻具,通过芯轴实现钻压、转速等钻井参数的调整。钻井液主体部分通过芯轴中间流道过流,如图3所示黄色箭头。套在芯轴上的导向外筒不受其影响,基本上处于静止或缓慢转动状态。钻头位置存在流体压差,利用小排量钻井液驱动推靠机构与井眼高边相互作用,对钻具实现静态推靠。当井斜角超出设计范围时,位于导向外筒内的偏重单元受到重力作用旋转,带动下端的上环形阀转到工具低边位置,并保持在一定的动态稳定精度范围内;位于下环形阀上高边的流道口打开,小排量的钻井液流入导向外筒高边位置的高压流道(如图3所示红色箭头),流入相应的活塞腔并推动活塞沿径向滑动,驱动翼肋向外伸出静态推靠井壁,给井眼高边位置施加静态推靠力,推动钻具向井眼低边方向偏转,从而实现钻进中的纠斜。
2. 环形动静盘阀结构及流道设计
2.1 动静盘阀间摩擦阻力的计算
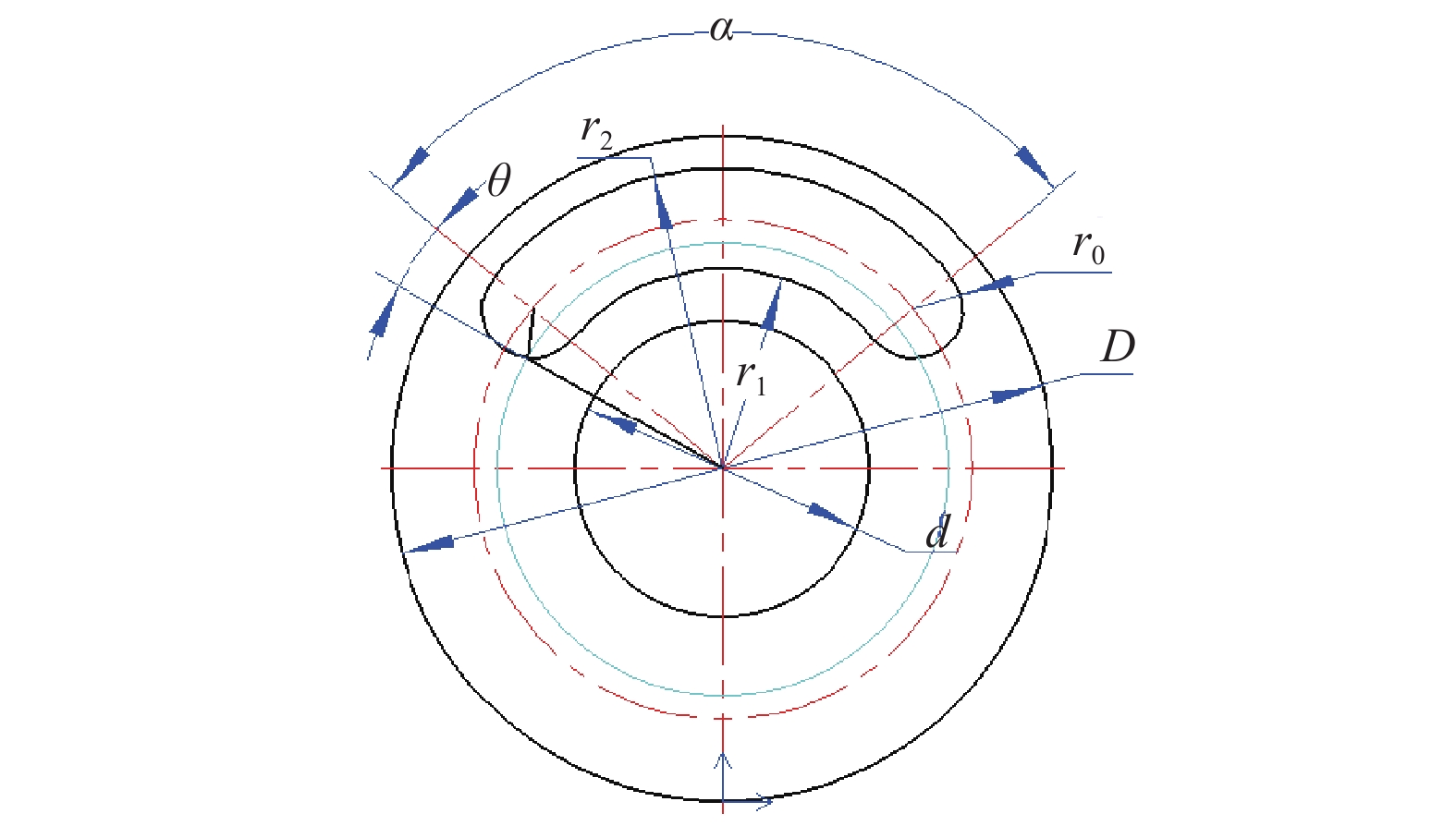
盘阀间的摩擦阻力矩由动静盘阀组之间存在的压力差及上下盘阀的相对转动产生,常规上盘阀结构如图4所示(
α 为腰孔开孔角度,(°);θ 为腰孔两端圆弧张开角度,(°);r0为腰孔两端圆弧半径,mm;r1,r2分别为上盘阀腰孔的内、外半径,mm;d为上盘阀的内径,mm;D为上盘阀的外径,mm)。盘阀间的摩擦阻力矩Tp可分为3部分进行计算,即:
Tp=Tp1+Tp2+Tp3 (1) 式中:
Tp1 为上盘阀半径r在[d/2,r1 ]的摩擦阻力矩,N·m;Tp2 为上盘阀半径r在(r1 ,r2 )的摩擦阻力矩,N·m;Tp3 为上盘阀半径r在[r2 ,D/2]的摩擦阻力矩,N·m。当上盘阀半径r位于[d/2,
r1 ]时,有:Tp1=∫r1d22μvpr2dr=23μvp(r31−d38) (2) 当上盘阀半径r位于(
r1 ,r2 )时,有:Tp2=∫r2r1(2p−α−2θ)r2dr (3) 当上盘阀半径r位于[
r2 ,D/2]时,计算摩擦力矩的方法与r位于[d/2,r1 ]时相同,有:Tp3=∫D2r22μvpr2dr=23μvp(D38−r32) (4) 则盘阀总的摩擦力矩为:
Tp=23μvp(r31−d38)+∫r2r1{2p−α−2arccos[r2+r1r2r(r1+r2)]}r2dr+23μvp(D38−r32) (5) 式中:
μv 为盘阀间的摩擦因数;p 为动静盘阀间的静水压力,MPa。焕发由式(5)可以看出,Tp与
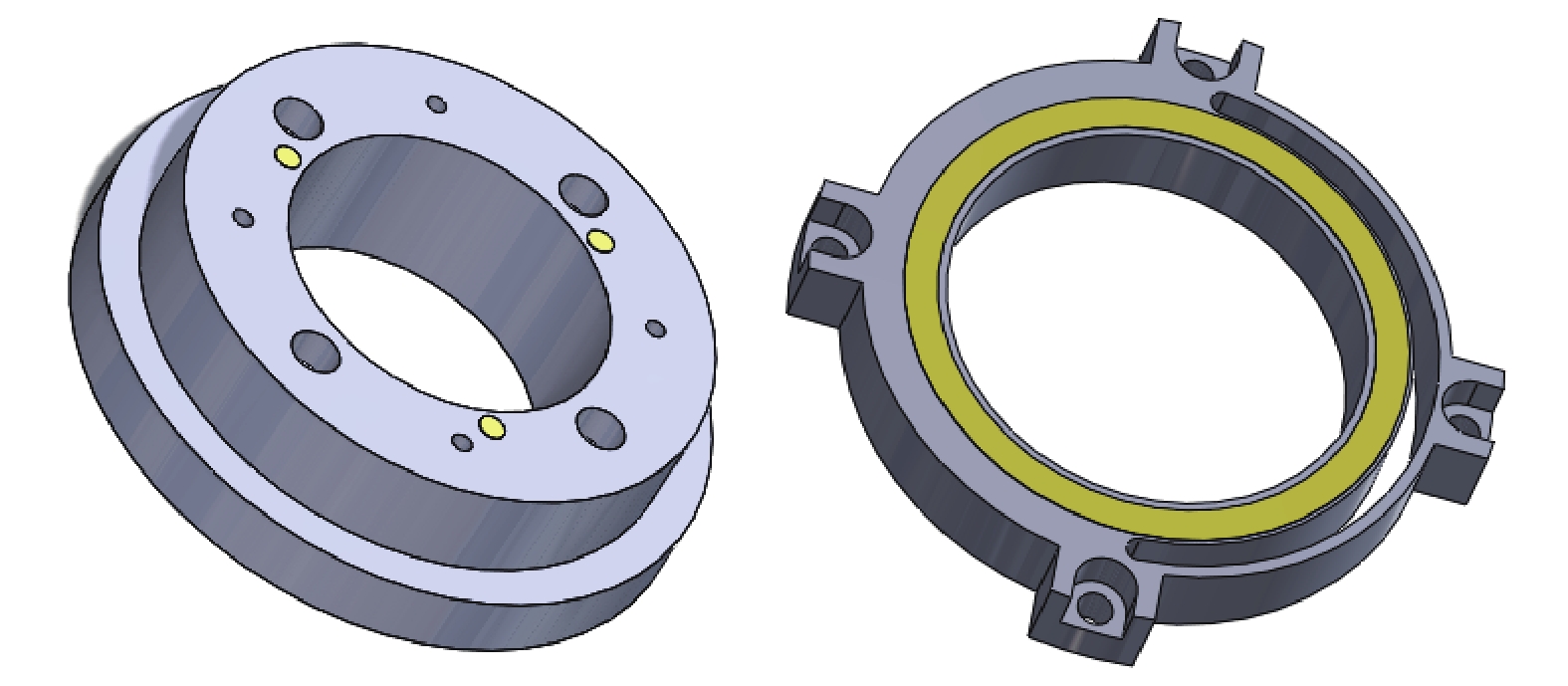
μ ,p 和r3 成正比。在实际设计过程中,p 往往固定不变,μv 的取值一般较小,变化范围也比较小。因此,减小r 是降低摩擦力矩最有效的方式。从另外一个角度考虑,盘阀的摩阻与半径的平方成正比,而半径的平方为盘阀面积,因此需要考虑减小盘阀接触面积。将与盘阀相配合的阀座设计为如图5所示的结构,阀座处采用凸台形式,凸台直径为
D0 ,其所在中心处直径为Df ,数量为3个。凸台处摩阻的计算公式为:
Fn=nπpbR2 (6) 式中:
Fn 为凸台处正压力,N;n为凸台数,此处取3;pb 为钻头压降,MPa;R为凸台半径,mm,此处取D0/2 。该处的摩擦力为:
Ff=Fnμv (7) 式中:
Ff 为凸台处的摩擦力,N。则摩阻力矩为:
Tp=FfDf2 (8) 为有效减小盘阀上下流体压力的作用面积,从而降低盘阀间的摩擦阻力,盘阀采用如图5所示凸台接触式结构。凸台结构使动静上下盘阀组间存在间隙,产生一定排量的泄流,而泄流量的大小直接关系到钻具各个推靠机构上侧向作用力的大小,进而对钻具的纠斜效果产生影响。因此,设计环阀间隙是否合理,是实现可控分流保压的关键,需要对盘阀缝隙流动开展有限元数值模拟分析,为盘阀结构的设计及优化提供依据。
2.2 环阀间隙的有限元计算分析
2.2.1 分析方法与湍流模型
采用计算流体动力学(computational fluid dynamics,CFD)方法研究盘阀间隙对钻具内部流场的影响,模拟分析了恒定排量条件下钻具内部流场的压力变化。CFD采用有限体积法进行离散化,以物体运动三大守恒定律为基础,推导出复杂流场中流体运动的控制方程。
目前应用于计算流体力学的湍流模型,主要包括代数湍流模型和运输方程湍流模型2大类。代数湍流模型主要为增强黏度模型,其计算精度一般低于运输方程模型。运输方程模型采用剪切应力输运(shear stress transport,SST)
κ−ω 模型,该模型通过混合函数在边界层内使用κ−ω 模型,在边界层之外的湍流核心区使用κ−ε 模型,可以有效预测逆压梯度条件下流体分离的开始点和分离区大小,并快速获得收敛解[19–20]。SSTκ−ω 模型的湍动能运输方程及湍流比耗散方程分别为:∂ρκ∂t+∂∂xj[ρvjκ−(μ+σκμt)]=τijSij−β∗ρωκ (9) ∂ρω∂t+∂∂xj[ρvjω−(μ+σωμt)∂ω∂xj]=Pω−βcρω2+2(1−F1)ρσωω∂κ∂ω∂xj∂xj (10) μt=ρκω (11) 式中:ρ为流体密度,kg/m3;κ为湍动动能,J;
xj 为空间坐标,m;vj 为速度分量,m/s;μ 为分子黏度,Pa·s;μt为t时刻的分子黏度,Pa·s;σκ 为湍动能的普朗特常量;τij 为湍流应力张量,Pa;Sij 为应变率张量,1/s;β∗ 为湍流衰减系数;ω为湍流比耗散,1/s;βc 和σω 为经验常数;F1 为SST模型的混合函数;Pω 为ω 生成项,与平均速度梯度等有关。Pω 的表达式为:Pω=2γρ(Sij−ωSnnSij3)−2ρκSij3 (12) 式中:
γ 为模型参数;Snn 为克罗内克算子。雷诺应力的涡黏性模型为:
τij=2μt(Sij−SnnSij3)−2ρκSij3 (13) 以水为不可压缩流体介质(
ρ=1.0 kg/L),马赫数很低,雷诺数很高。基于上述分析,模拟分析用基本方程:\left\{ {\begin{array}{*{20}{l}} {\rho \left( {{\boldsymbol{v}} \cdot \nabla } \right){\boldsymbol{v}} = \nabla \cdot \left[ { - p{\boldsymbol{I}} + \left( {\mu + {\mu _t}} \right)\left( {\nabla {\boldsymbol{v}} + {{\left( {\nabla {\boldsymbol{v}}} \right)}^T}} \right)} \right] + {\boldsymbol{F}}} \\ {\rho \nabla \cdot {\boldsymbol{v}} = 0} \\ {\rho \left( {{\boldsymbol{v}} \cdot \nabla } \right)\kappa = \nabla \cdot \left[ {\left( {\mu + {\mu _t}{\sigma _\kappa}} \right)\nabla \kappa} \right] + \tau {i_j}{S_{ij}} - {\beta ^*}\rho \omega \kappa} \\ \rho \left( {{\boldsymbol{v}} \cdot \nabla } \right)\omega = \nabla \cdot \left[ {\left( {\mu + {\mu _t}{\sigma _\omega }} \right)\nabla \omega } \right] + \dfrac{\gamma }{{{\mu _t}}}\rho p - \rho {\beta _{\mathrm{c}}}{\omega ^2} +\\ 2\left( {1 - {F_1}} \right)\dfrac{{{\sigma _\omega }\rho }}{\omega }\nabla \kappa \cdot \nabla \omega \end{array}} \right. (14) 式中:v为速度场;I为单位矩阵;T为温度,K;F为外力场,包括重力、磁力等;
\nabla 表示梯度运算。壁距离是CFD模拟中关键的几何量之一,指流体中某一点到物体边界或壁面的垂直距离,用于描述流体与固体表面之间的关系。壁距离
{l_{\mathrm{w}}} 初始化方程为:\left\{ {\begin{array}{*{20}{l}} {\nabla G \cdot \nabla G + {\sigma _\mathrm{w}}G\left( {\nabla \cdot \nabla G} \right) = \left( {1 - 2{\sigma _\mathrm{w}}} \right){G^4}} \\ {{l_\mathrm{w}} = \dfrac{1}{G} - \dfrac{l_\mathrm{ref}}{2}} \end{array}} \right. (15) 式中:G为壁距离倒数,1/m;
{l_{{\mathrm{ref}}}} 为参考比例长度,m。入口控制方程为:
\left\{\begin{array}{*{20}{l}}\boldsymbol{v}=-\dfrac{M_{\mathrm{f}}}{\rho}\boldsymbol{n} \\ \nabla G\cdot\boldsymbol{n}=0 \\ M_{\mathrm{f}}=\dfrac{\rho V_{\mathrm{L}}}{\text{π}R^2t}\end{array}\right. (16) 式中:n为法向单位向量;
{M_{\mathrm{f}}} 为逐点质量流率,kg/(m2·s);{V_{\mathrm{L}}} 为入口处单位时间通过流体的体积,m3;R为入口处半径,m;t为时间,s。出口控制方程为:
\left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{n}}^T}\left[ { - p{\boldsymbol{I}} + \left( {\mu + {\mu _T}} \right)\left( {\nabla {\boldsymbol{v}} + {{\left( {\nabla {\boldsymbol{v}}} \right)}^T}} \right)} \right]{\boldsymbol{n}} {\hat p{_0}} } \\ {{\hat p{_0}} < {p_0},{\boldsymbol{v}} \cdot t = 0} \\ {\nabla \kappa \cdot {\boldsymbol{n}} = 0,\nabla \omega \cdot {\boldsymbol{n}} = 0,\nabla G \cdot {\boldsymbol{n}} = 0} \end{array}} \right. (17) 式中:
{{\hat p_0}} ,{p_0} 分别为出口预设压力和出口理论压力,MPa;μT为温度T时的分子黏度,Pa·s。模拟过程中,设流体通道壁为无滑移边界条件,则边界条件为:
\left\{\begin{array}{l} {\boldsymbol{v}} = 0\\k = 0\\\omega = \mathop {\lim }\limits_{{l_{\mathrm{w}}} \to 0} \frac{{6v}}{{{\beta _1}l _{\mathrm{w}}^2}}\\{l _{\mathrm{w}}} = 0 \end{array}\right. (18) CFD模拟用主要参数κ为0.41,β*为9/100,βc1为0.075,βc2为
0.0828 ,γ1为5/9,γ2为0.44,σκ1为0.85,σκ2为1,σω1为0.5,σω2为0.856。综合分析这些参数,基于ANSYS Workbench平台构建了三维瞬态流程模型:根据图6流道尺寸进行参数化建模,特征尺寸公差小于0.01 mm;采用边界层加密方法,近壁面第一层厚度为0.02 mm;选用SST\kappa - \omega 湍流模型进行求解设置,并进行网格无关性分析,结果表明模型可靠。2.2.2 模拟分析结果
静态推靠机械式垂钻工具的工作原理主要是,在不影响其工作压力的前提下,分流部分流体通过工具,并在偏重平台的作用下利用上、下盘阀产生高低压配流,高压部分流体推动活塞径向移动,将翼肋沿径向推出,从而产生纠斜效果。这个过程中,不同流体的压力有着重要作用:首先是系统压力,为了不影响钻具正常工作,需保证系统增加该垂钻工具后,在一定的系统流量(60 L/s)下通过调节钻头水眼的尺寸保证钻具正常工作,即系统压力不会因增加该工具而无法调整至正常状态,系统压力一般要求在3~5 MPa;其次是盘阀处流体压力,由于盘阀处的流体压力作用于上下盘阀接触表面,由于盘阀间存在摩擦因数,该部分正压力产生阻碍盘阀间相对运动的阻力,因此该部分压力往往要求越小越好,该处压力越小,同样偏心块作用下偏重平台的灵敏度就越高,即要达到相同灵敏度所需偏重平台的长度就越小;再次是推靠活塞处压力,该部分压力直接决定执行机构推靠力的大小,根据实际纠斜需求,要求工具达到10~20 kN推靠力,根据计算,推靠活塞处系统压力应在1~2 MPa。
由以上分析可知,进行工具内部流体模拟的目的有2个:1)确定怎样的流道设计可以满足工具的使用要求,即在60 L/s的流量作用下,系统压力可达到3~5 MPa,推靠活塞处的压力为1~2 MPa,同时盘阀处的流体压力尽可能小;2)通过模拟得到可保证工具正常工作的钻头水眼组合。
分析工具内部流道,得到其简化流道及模拟模型,如图6所示。建立模拟模型时作了如下假设:
1)盘阀间无间隙。静态推靠机械式垂钻工具盘阀间为凸台式结构,上下盘阀间有0.5 mm间隙。由于该间隙太小,而工具实际尺寸较大,若在模拟过程中包含该缝隙,将导致模拟整体网格数量及计算量大幅增加,因此在模拟过程中将该间隙忽略,并针对该缝隙流进行了专门分析。
2)上下轴承缝隙泄流简化为一当量直径孔泄流。由于径向轴承在使用过程中,公轴承与母轴承之间往往需要有约0.3 mm的间隙,在轴承工作时会形成泄漏流动。泄流通道的几何形状对流体流动的影响主要由其直径决定,将复杂的缝隙流动简化为具有相同流动特性的当量直径孔流动,可以更方便地利用已有的理论和经验公式进行计算和分析。这种简化假设允许在不考虑缝隙的详细形状和复杂性情况下,仍能准确预测流体的运动状态。
模拟模型中各进出口及系统边界条件参数:入口直径为55.0 mm,上轴承泄流当量直径为10.0 mm,下轴承泄流当量直径为10.0 mm,推靠活塞泄流口直径为3.0 mm,入口流量为60 L/s。
根据伯努利方程,沿流线方向,流体的压强、流速的平方与高度的线性组合是一个常数C:
{p_{\mathrm{L}}} + \frac{1}{2}{\rho _{\mathrm{L}}}v_{\mathrm{L}}^2 + {\rho _{\mathrm{L}}}gh = C (19) 式中:
{p_{\mathrm{L}}} 为流场内部流体压力,MPa;{\rho _{\mathrm{L}}} 为钻井液的密度,kg/m3;{v_{\mathrm{L}}} 为钻井液的流速,m/s;h为液流位置距地面的距离,m。在恒定排量钻井过程中,当钻具内部流场发生横截面积变化时,因钻井液流速变化,横截面积变化前后钻具内部钻井液压力的变化量为
\Delta {p_{\mathrm{L}}} (忽略液流位置距地面距离的变化及钻具内部沿程压降的影响),\Delta {p_{\mathrm{L}}} 可以表示为:\Delta {p_{\mathrm{L}}} = {p_{{\mathrm{L}}1}} - {p_{{\mathrm{L}}2}} = \frac{1}{2}{\rho _{\mathrm{L}}}{\left( {\frac{{{Q_{\mathrm{L}}}}}{{{S_{D2}}}}} \right)^2} - \frac{1}{2}{\rho _{\mathrm{L}}}{\left( {\frac{{{Q_{\mathrm{L}}}}}{{{S_{D1}}}}} \right)^2} (20) 式中:pL1,pL2为钻具内部流场横截面积变化前后的流场压力,MPa;QL为钻井液流量,m3/s;SD1,SD2为钻具内部流场横截面积变化前后的横截面积,m2。
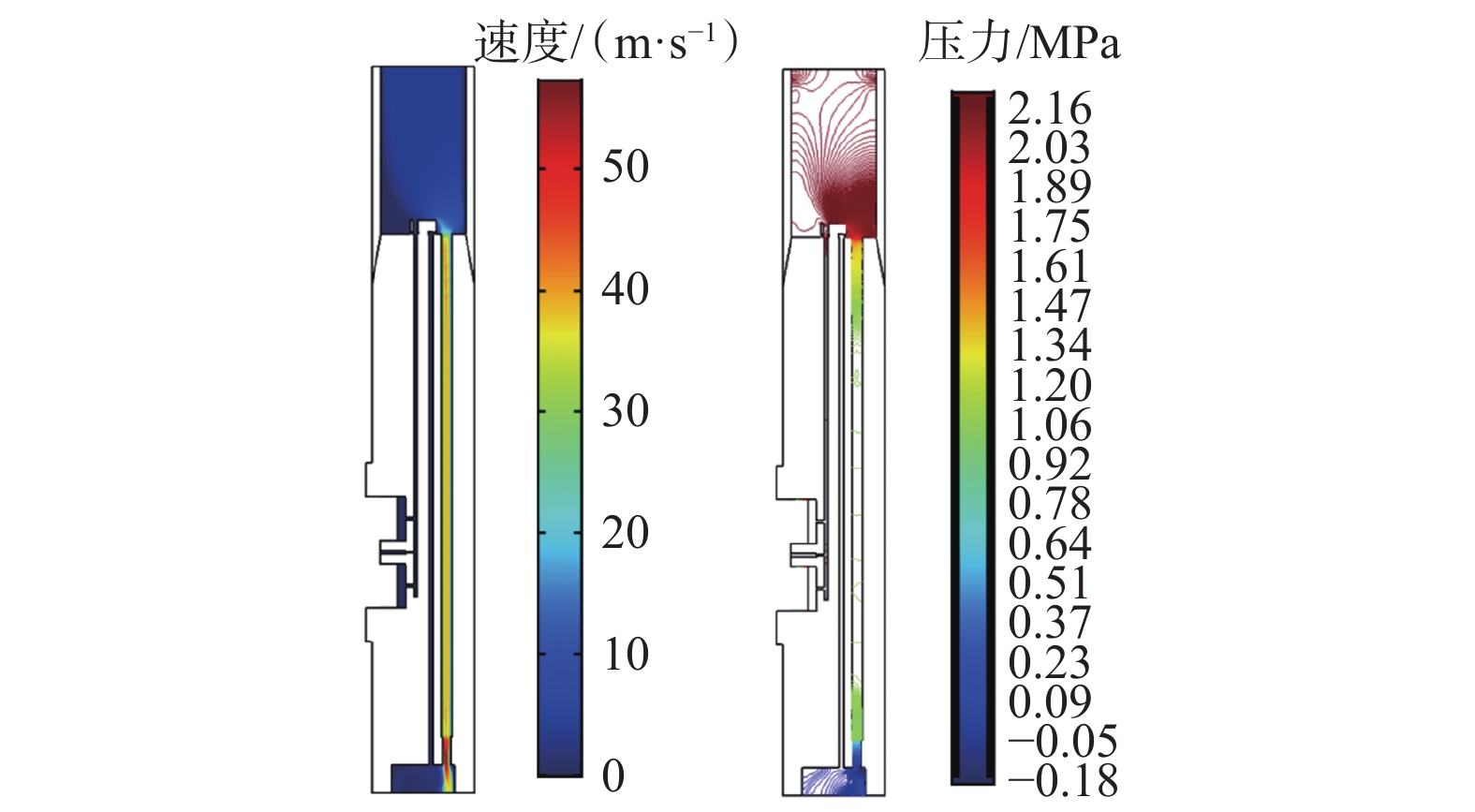
钻具内部流场模拟用主要设计及工艺参数:入口直径为55.0 mm,喷嘴半径为5.0 mm,喷嘴为5个,流量为3 600 L/min,活塞间隙为0.1 mm,出口压力为0 MPa。模拟分析中,主要考虑钻具内部压降,忽略钻具外部环空中钻井液的压力,因此设定出口压力为0 MPa。若不考虑活塞间隙处的出口,无盘阀间隙时,可得钻具内部流场压降约为2.92 MPa。设定活塞间隙为出口后,通过模拟计算出盘阀处的最大压力为2.16 MPa,小于理论计算结果,与实际情况基本吻合,如图7所示。
盘阀的缝隙分别为0.2,0.5,1.0和5.0 mm时,钻具内部流场的流速和压力如图8所示。
从图8可以看出,随着盘阀间隙逐步增大,钻具内部流场的最大流速和最大压力均呈现逐渐减小的趋势,但钻具内部最大流速和最大压力的位置基本保持一致,最大流速出现在等效钻头喷嘴位置,最大压力位于盘阀上方。
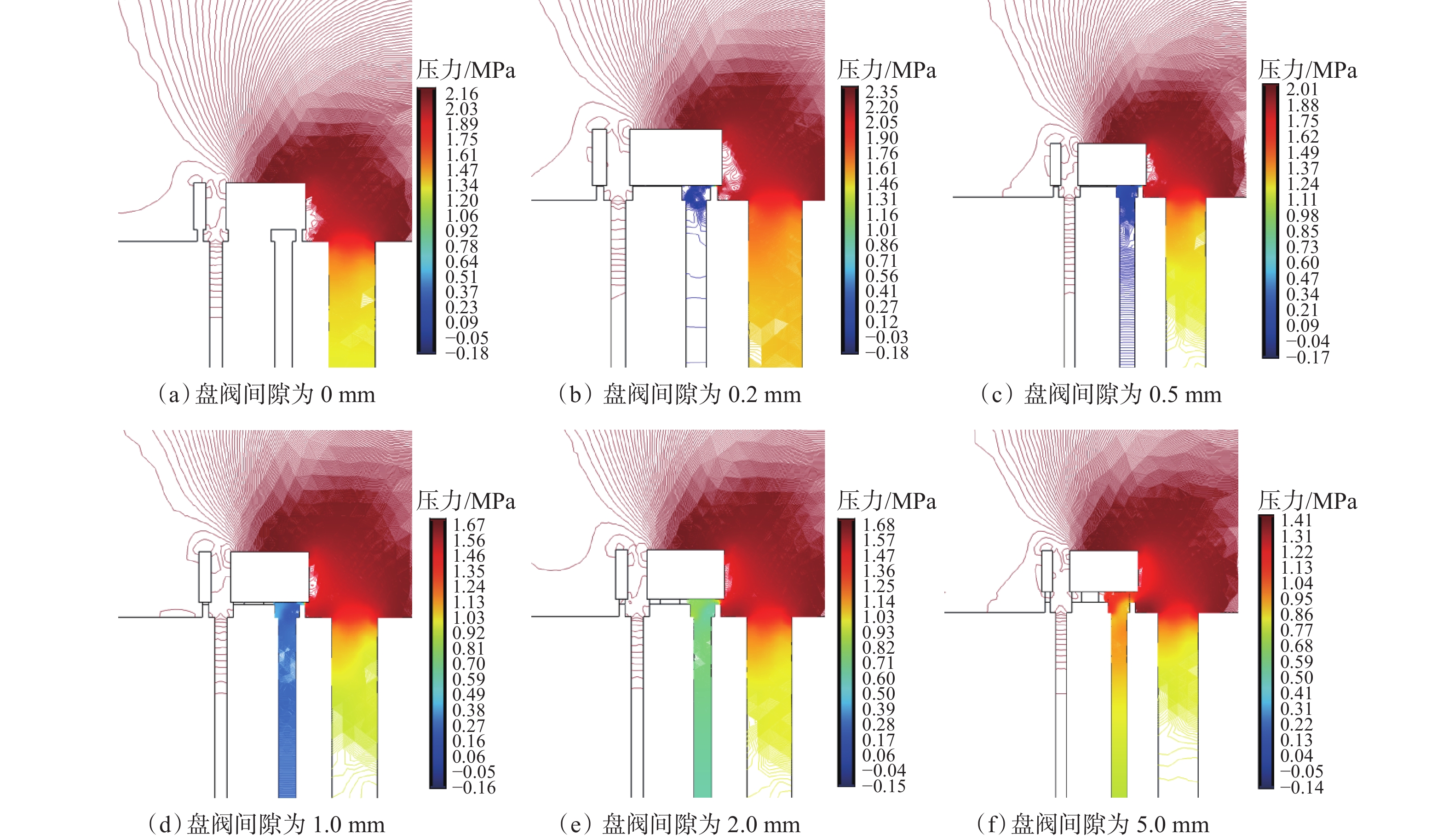
盘阀间隙对盘阀附近流场影响的局部放大图见图9。从图9可以看出,当盘阀间隙小于0.5 mm时,低压钻井液流道的内部压力较小,且随着盘阀间隙增大,低压钻井液流道的内部压力缓慢升高;当盘阀间隙为1.0和2.0 mm时,低压钻井液流道的压力明显增大,且增大速度较盘阀间隙小于0.5 mm时明显加快;当盘阀间隙为5.0 mm时,盘阀右侧钻井液流道压力基本保持一致,表明此时不再存在低压钻井液流道,盘阀失去密封作用。
分析了钻具活塞两侧压差及盘阀下部井眼高边与低边钻井液通道压差变化随盘阀间隙的变化趋势,结果如图10所示。
由图10可知,为保证钻具正常工作,须严格控制盘阀的泄流量,应将盘阀间隙控制在0.5 mm以下,此时盘阀下井眼低边一侧钻井液通道内的压力与盘阀间无缝隙时的变化较小,在允许盘阀一定泄流量的前提下,起到一定的“密封”作用,保证钻具正常工作。通过以上分析,最终确定上下盘阀间隙为0.5 mm,上下盘阀凸台高度均为0.25 mm。
3. 地面台架试验
在全尺寸试验台架开展了ϕ177.8 mm静态推靠机械式垂钻工具的地面水力台架试验,用以验证该工具的主要功能。具体为:1)验证该工具在模拟现场机泵排量及压差下的整机性能;2)验证该工具在−4°~4°井斜角变化范围内推靠翼肋的启动角度,确定重力测斜稳定平台机构的响应精度;3)验证该工具在不同压差下翼肋推靠力的范围及互锁功能;4)验证不同排量下该工具两端轴承处、推靠翼肋处的泄流情况。
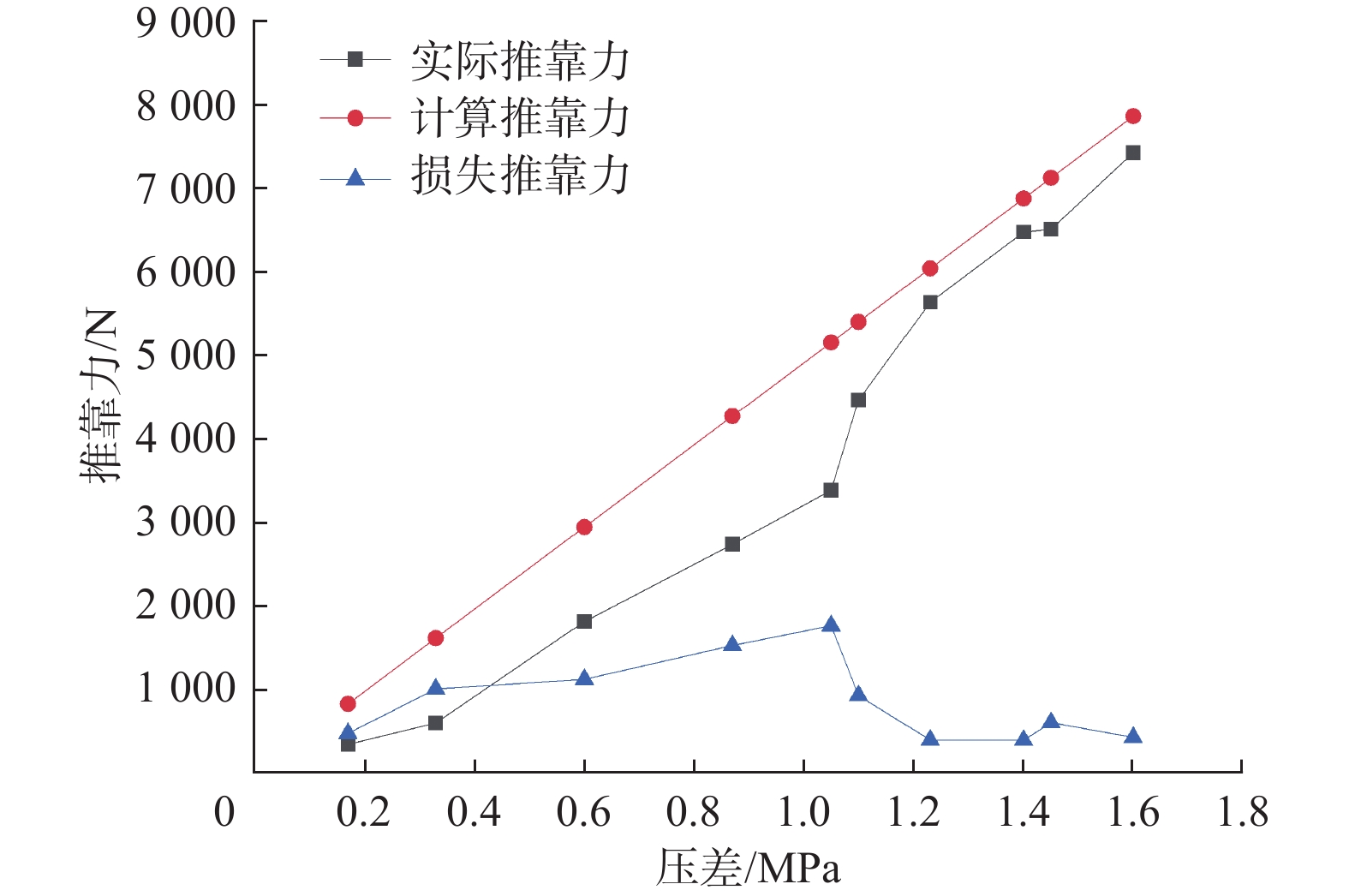
根据试验数据得到了推靠力随压差变化的曲线、工具内部无效压耗随排量变化的曲线,分别如图11、图12所示。
由图11、图12可知,翼肋启动大约需0.3 MPa,推靠力随着压差增大基本为线性增加,有效压耗占比(推靠力)最大为94.46%,平均在80%左右。静态推靠机械式垂钻工具两端PDC复合轴承的泄漏,使该工具内部存在无效压力损耗,在试验压差范围内无效压耗平均为0.27 MPa。通过调整推靠翼肋的方位,观察翼肋出水孔的出水情况,90°方位位置只有1个推靠翼肋出水,表明稳定平台上下环阀的密封正常,只有高边导流孔导通,其他孔没有导通。转动外筒至45°方位,2个推靠翼肋同时推出,2个推靠翼肋的出水孔均衡出水,表明稳定平台导向正常,密封性良好。转动外筒至75°方位,2个高边翼肋同时推出,出水不均衡,靠近高边位置的出水强度大,远离高边位置的出水强度小,表明稳定平台控制动静盘阀组导向分流正常,密封保压性能指标达到了预期的设计要求。
4. 结论与建议
1)为研制高温、强振条件下经济、安全、可靠的静态推靠机械式垂钻工具,对其关键部件导流盘阀进行了研究与设计。根据盘阀摩阻力计算结果,为减小盘阀上下流体压力的作用面积,从而减小盘阀间摩擦阻力的作用,将动静盘阀组之间设计为凸台接触式结构。
2)通过采用有限元法对上下盘阀之间的缝隙流动进行模拟,确定上下盘阀间隙应控制在0.5 mm,上下盘阀凸台高度均控制在0.25 mm。
3)在全尺寸试验台架开展了ϕ177.8 mm静态推靠机械式垂钻工具的地面水力台架试验,验证了所设计盘阀的密封性、导流性。
4)静态推靠机械式垂钻工具采用纯机械部件,集合了国内外垂钻工具的技术优势,能够克服高温、高转速及振动冲击等制约条件。建议加快现场试验及推广应用,优化迭代,为高陡构造等易斜地区的防斜打快提供低成本的钻井工具。
-
-
[1] 苏义脑. 油气井工程中的一个新领域:井下控制工程学浅谈[J]. 地质科技情报,2005,24(增刊1):1−8. SU Yinao. New field of oil and gas well engineering: discussion on theory of downhole control engineering[J]. Bulletin of Geological Science and Technology, 2005, 24(supplement 1): 1−8.
[2] 张绍槐. 现代导向钻井技术的新进展及发展方向[J]. 石油学报,2003,24(3):82–85. doi: 10.3321/j.issn:0253-2697.2003.03.018 ZHANG Shaohuai. New progress and development direction of modern steering drilling techniques[J]. Acta Petrolei Sinica, 2003, 24(3): 82–85. doi: 10.3321/j.issn:0253-2697.2003.03.018
[3] 孙峰,王瑞和. 垂钻系统单轴稳定平台测量算法[J]. 中国石油大学学报(自然科学版),2011,35(4):85–88. doi: 10.3969/j.issn.1673-5005.2011.04.015 SUN Feng, WANG Ruihe. Measurement algorithm in single-axis stabilized platform of vertical drilling system[J]. Journal of China University of Petroleum(Edition of Natural Science), 2011, 35(4): 85–88. doi: 10.3969/j.issn.1673-5005.2011.04.015
[4] 孙峰,吕官云,马清明. 捷联式自动垂直钻井系统[J]. 石油学报,2011,32(2):360–363. doi: 10.7623/syxb201102029 SUN Feng, LYU Guanyun, MA Qingming. A strap-down automatic vertical drilling system[J]. Acta Petrolei Sinica, 2011, 32(2): 360–363. doi: 10.7623/syxb201102029
[5] 孙峰,吕官云,陈威,等. 捷联式自动垂直钻井稳定平台控制系统仿真研究[J]. 石油钻探技术,2011,39(5):91–95. doi: 10.3969/j.issn.1001-0890.2011.05.020 SUN Feng, LYU Guanyun, CHEN Wei, et al. Research on strap-down automatic vertical drilling system with the simulation of stable platform control[J]. Drilling Petroleum Techniques, 2011, 39(5): 91–95. doi: 10.3969/j.issn.1001-0890.2011.05.020
[6] 孙峰,陈威,王义峰. ϕ311 mm自动垂直钻井系统在宣页1井的应用[J]. 石油机械,2011,39(4):31–32. SUN Feng, CHEN Wei, WANG Yifeng. The application of the ϕ311 mm automatic vertical drilling system in No. 1 Well of Xuanye[J]. China Petroleum Machinery, 2011, 39(4): 31–32.
[7] 柴麟,张凯,刘宝林,等. 自动垂直钻井工具分类及发展现状[J]. 石油机械,2020,48(1):1–11. CHAI Lin, ZHANG Kai, LIU Baolin, et al. Classification and development status of automatic vertical drilling tools[J]. China Petroleum Machinery, 2020, 48(1): 1–11.
[8] 吴小雄,段树军,王前敏,等. 旋转推靠式自动垂直钻井工具应用分析[J]. 机械工程师,2023(1):115–117. doi: 10.3969/j.issn.1002-2333.2023.1.jxgcs202301033 WU Xiaoxiong, DUAN Shujun, WANG Qianmin, et al. Application analysis of rotating and pushing type automatic vertical drilling tool[J]. Mechanical Engineer, 2023(1): 115–117. doi: 10.3969/j.issn.1002-2333.2023.1.jxgcs202301033
[9] 孙峰. 静态推靠机械式垂钻工具的研制及试验[J]. 石油机械,2025,53(3):32-37. SUN Feng. Development and test of static pushing mechanical vertical drilling tool[J]. China Petroleum Machinery, 2025, 53(3): 32-37.
[10] 马超群,张凯,柴麟,等. 机械式自动垂直钻具执行机构内部流场规律研究[J]. 工程设计学报,2022,29(3):384–393. doi: 10.3785/j.issn.1006-754X.2022.00.044 MA Chaoqun, ZHANG Kai, CHAI Lin, et al. Research on internal flow field law of mechanical automatic vertical drilling tool actuator[J]. Chinese Journal of Engineering Design, 2022, 29(3): 384–393. doi: 10.3785/j.issn.1006-754X.2022.00.044
[11] 康建涛,苏海峰,张川,等. BH-VDT大尺寸垂直钻井工具设计优化与应用[J]. 长江大学学报(自然科学版),2021,18(6):63–68. doi: 10.3969/j.issn.1673-1409.2021.06.009 KANG Jiantao, SU Haifeng, ZHANG Chuan, et al. Design optimization and application of BH-VDT large size vertical drilling tool[J]. Journal of Yangtze University (Natural Science Edition), 2021, 18(6): 63–68. doi: 10.3969/j.issn.1673-1409.2021.06.009
[12] 惠坤亮,吴小雄,游娜,等. 推靠式垂直钻井工具机械系统关键技术分析[J]. 机械工程师,2021(1):122–124. HUI Kunliang, WU Xiaoxiong, YOU Na, et al. Key technologies analysis on mechanical system of push-the-bit vertical drilling tool[J]. Mechanical Engineer, 2021(1): 122–124.
[13] RAMALAKSHMI M, DODAGOUDAR G R. Lateral response analysis of GRS bridge abutments under passive push[J]. Geotechnical Engineering Journal of the SEAGS & AGSSEA, 2018, 49(4): 49–54.
[14] 李立鑫,薛启龙,刘宝林,等. 机械式自动垂直钻具的纠斜行为及研究进展[J]. 西安石油大学学报(自然科学版),2018,33(1):90–97. doi: 10.3969/j.issn.1673-064X.2018.01.015 LI Lixin, XUE Qilong, LIU Baolin, et al. Straightening behavior analysis and research progress of mechanical automatic vertical drilling tools[J]. Journal of Xi’an Shiyou University (Natural Science Edition), 2018, 33(1): 90–97. doi: 10.3969/j.issn.1673-064X.2018.01.015
[15] TJEMSLAND T H H. Evaluation of measurement-while-drilling, telemetry methods and integration of control systems[D]. Stavanger: University of Stavanger, 2012.
[16] 李士斌,王业强,张立刚,等. 静态推靠式旋转导向控制方案分析及优化[J]. 石油钻采工艺,2015,37(4):12–15. LI Shibin, WANG Yeqiang, ZHANG Ligang, et al. Analysis and optimization of static push-the-bit rotary steering control scheme[J]. Oil Drilling & Production Technology, 2015, 37(4): 12–15.
[17] 史玉才,孙海芳,岳步江,等. 静态推靠式旋转导向钻井工具防自锁设计方法[J]. 中国石油大学学报(自然科学版),2017,41(5):80–86. doi: 10.3969/j.issn.1673-5005.2017.05.009 SHI Yucai, SUN Haifang, YUE Bujiang, et al. A design method to prevent self-locking of a static push-the-bit rotary steerable drilling tool[J]. Journal of China University of Petroleum (Edition of Natural Science), 2017, 41(5): 80–86. doi: 10.3969/j.issn.1673-5005.2017.05.009
[18] HYLAND K B, LAING M, MATHIESON G, et al. HPHT wells spudded utilising a rotary steerable system below a 26-in×36-in hole opener to improve tophole drilling performance[R]. SPE 189639, 2018.
[19] 曾宇,汪洪波,孙明波,等. SST湍流模型改进研究综述[J]. 航空学报,2023,44(9):98–129. ZENG Yu, WANG Hongbo, SUN Mingbo, et al. SST turbulence model improvements: review[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(9): 98–129.
[20] 赵立新,朱宝军. 不同湍流模型在旋流器数值模拟中的应用[J]. 石油机械,2008,36(5):56–60. ZHAO Lixin, ZHU Baojun. Application of different turbulence model in hydrocyclone numerical simulation[J]. China Petroleum Machinery, 2008, 36(5): 56–60.




 下载:
下载: