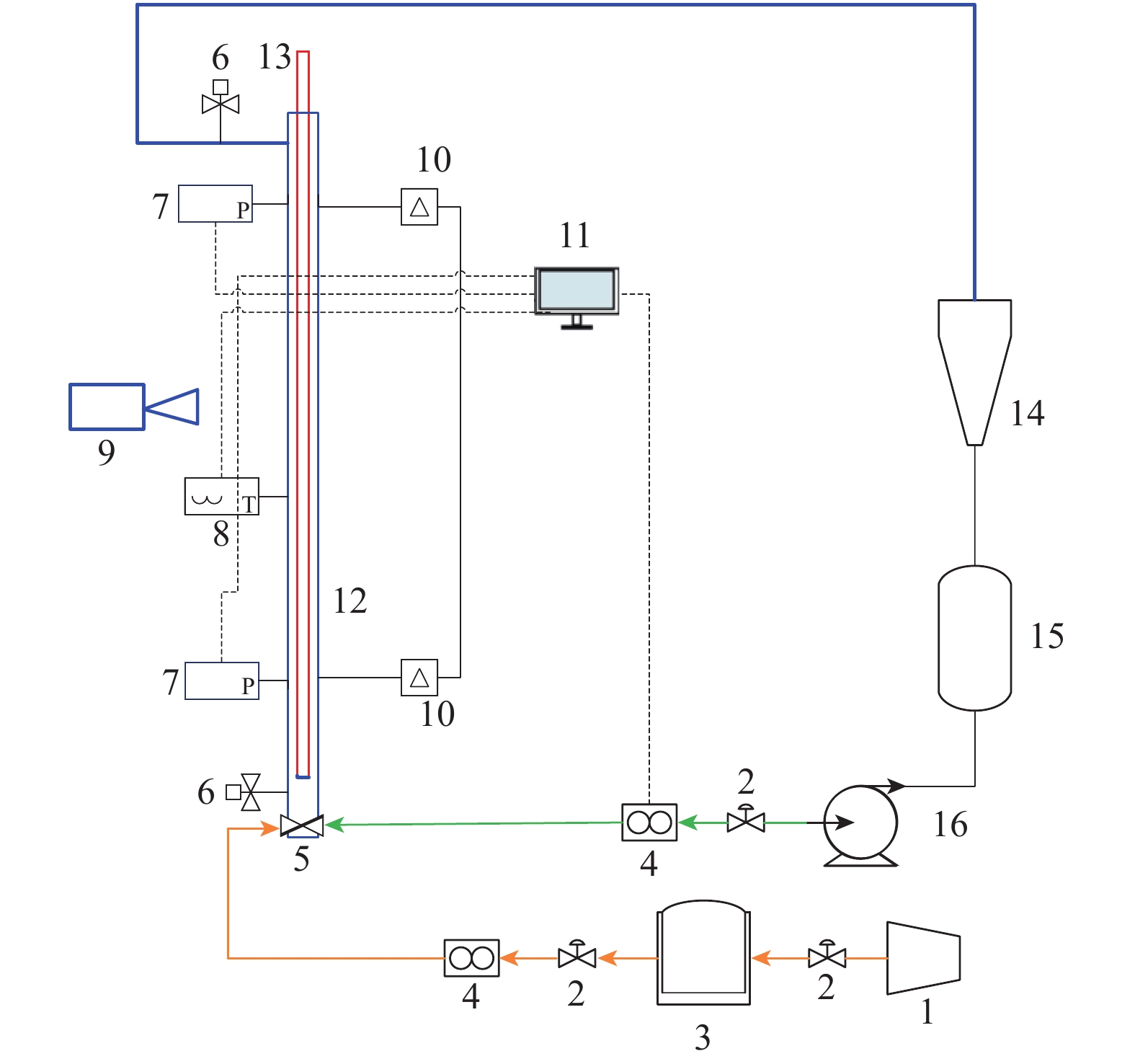
Pressure Drop Prediction Model for Vertically Upward Annular Flow in Annular Space of Oil Tube and Casing
-
摘要:
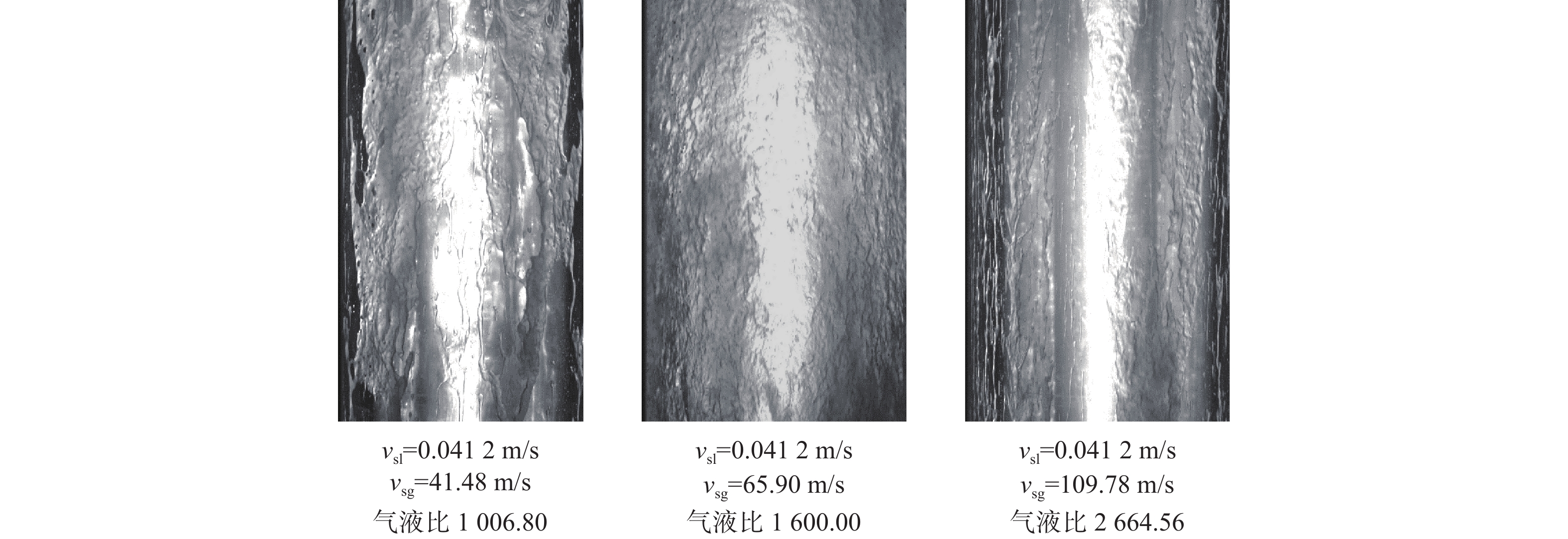
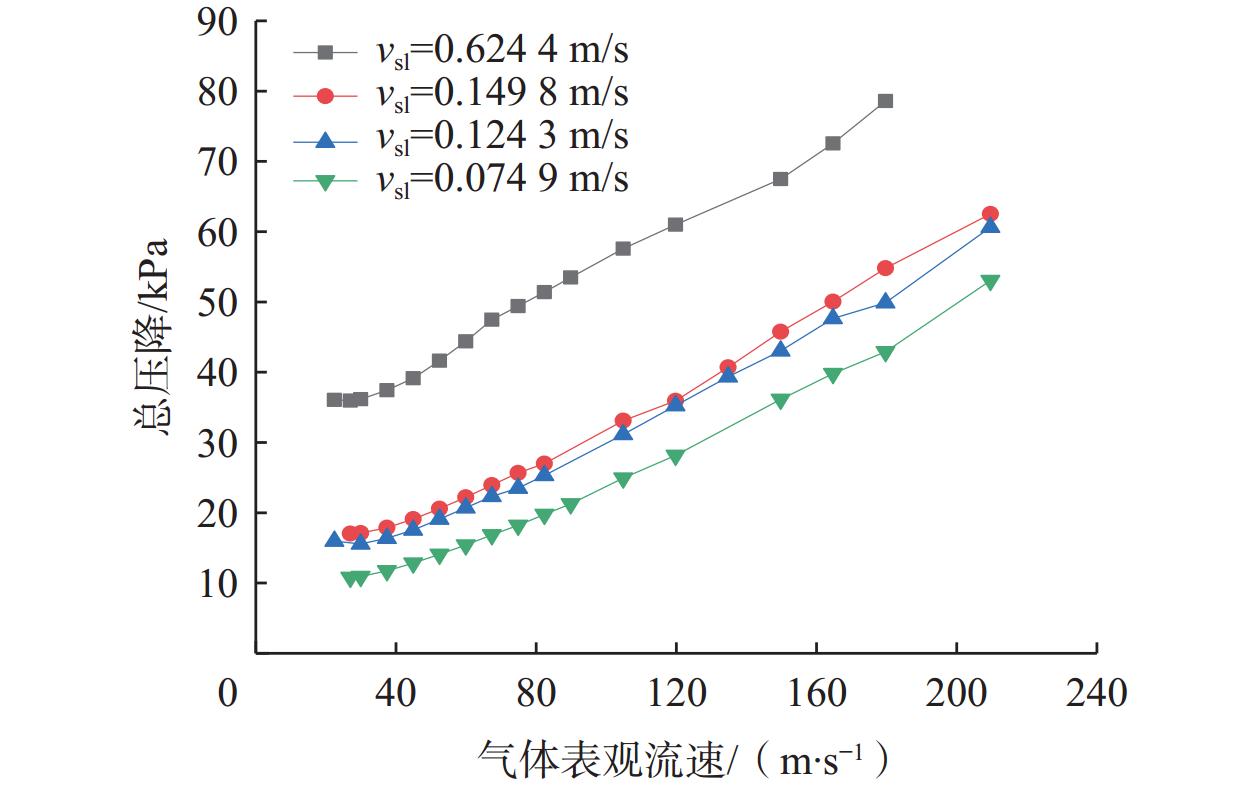
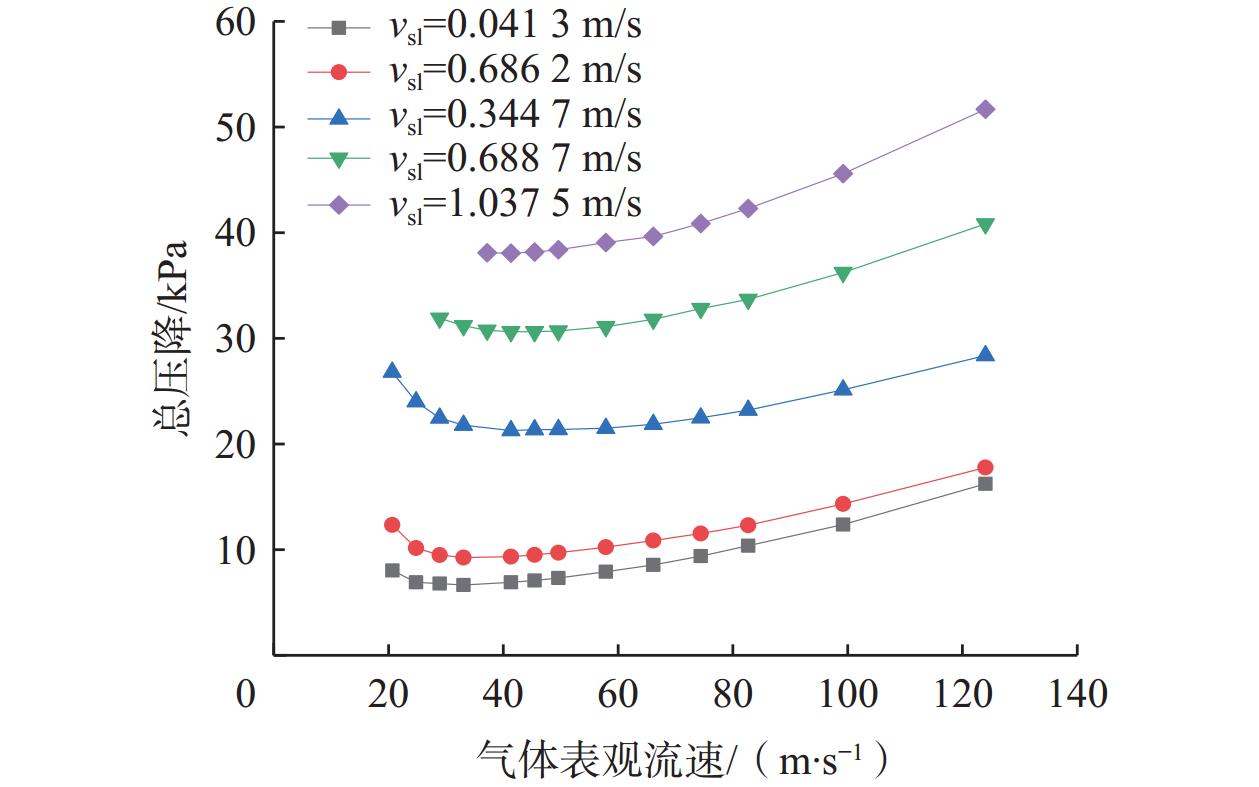
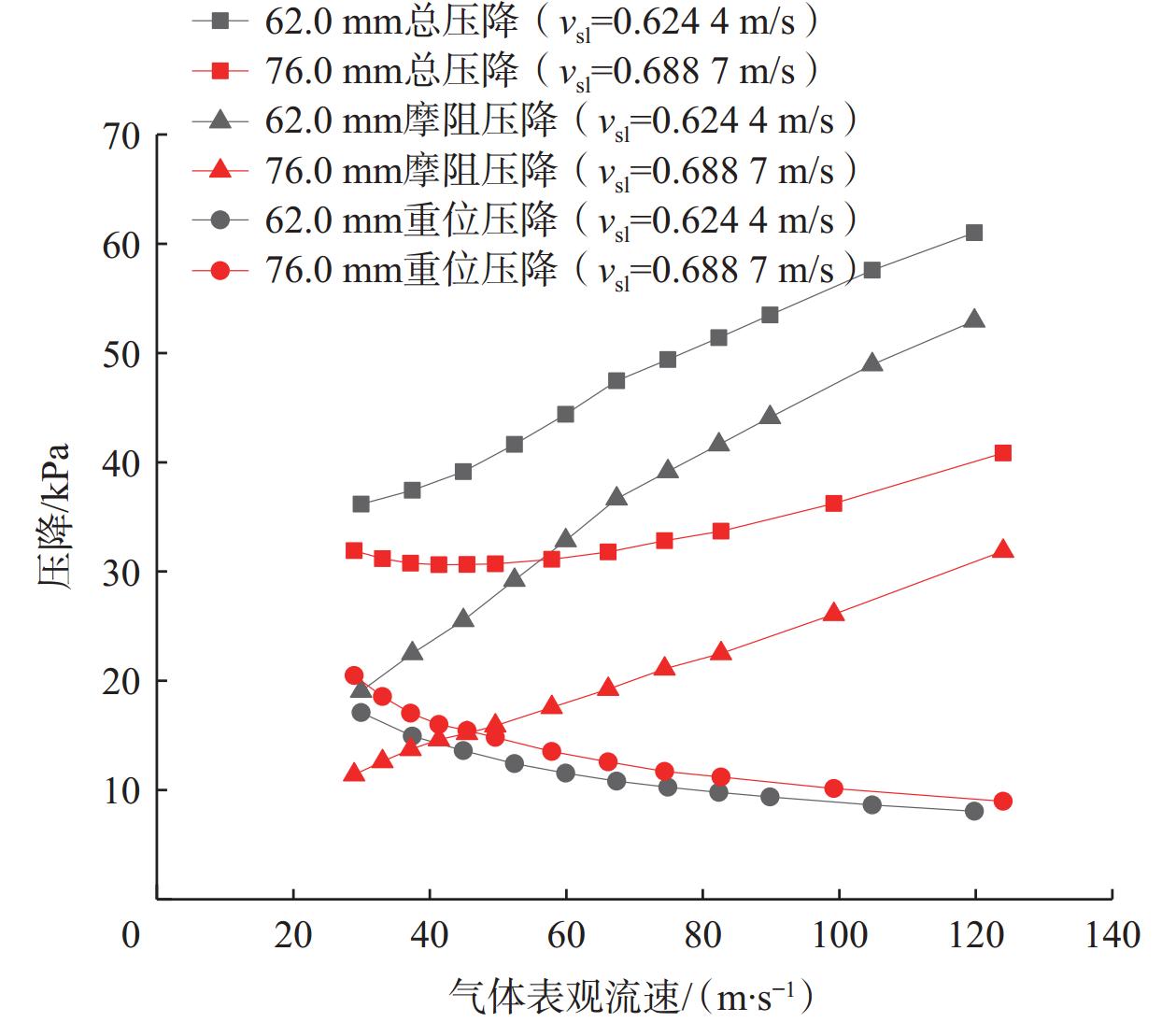
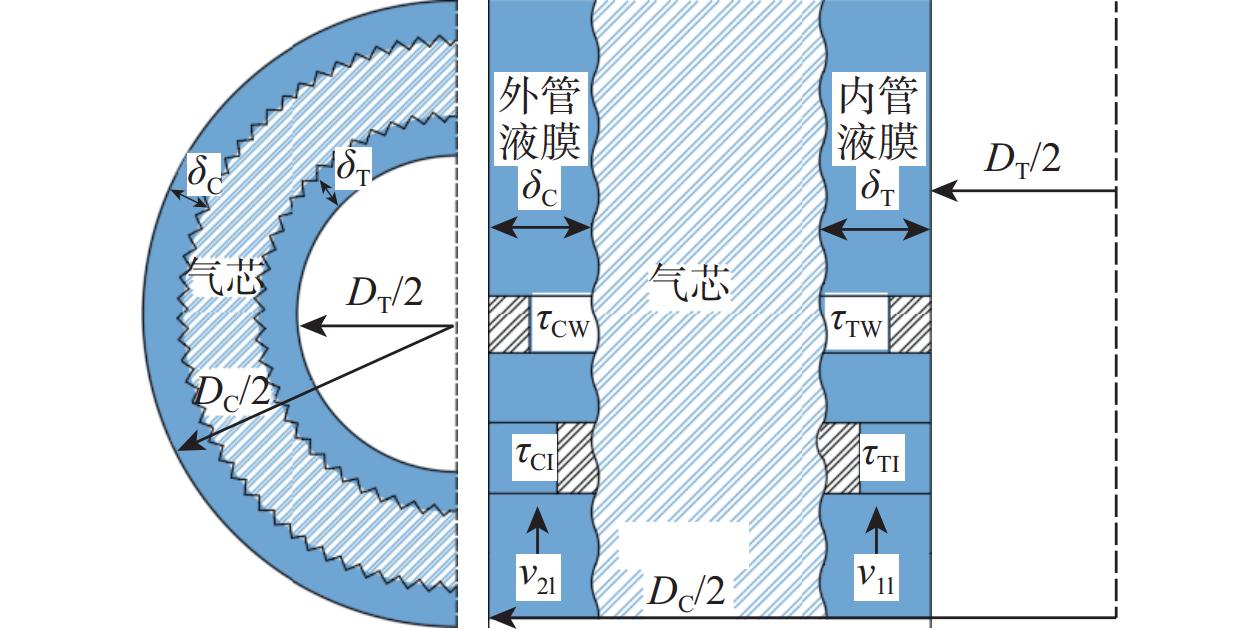
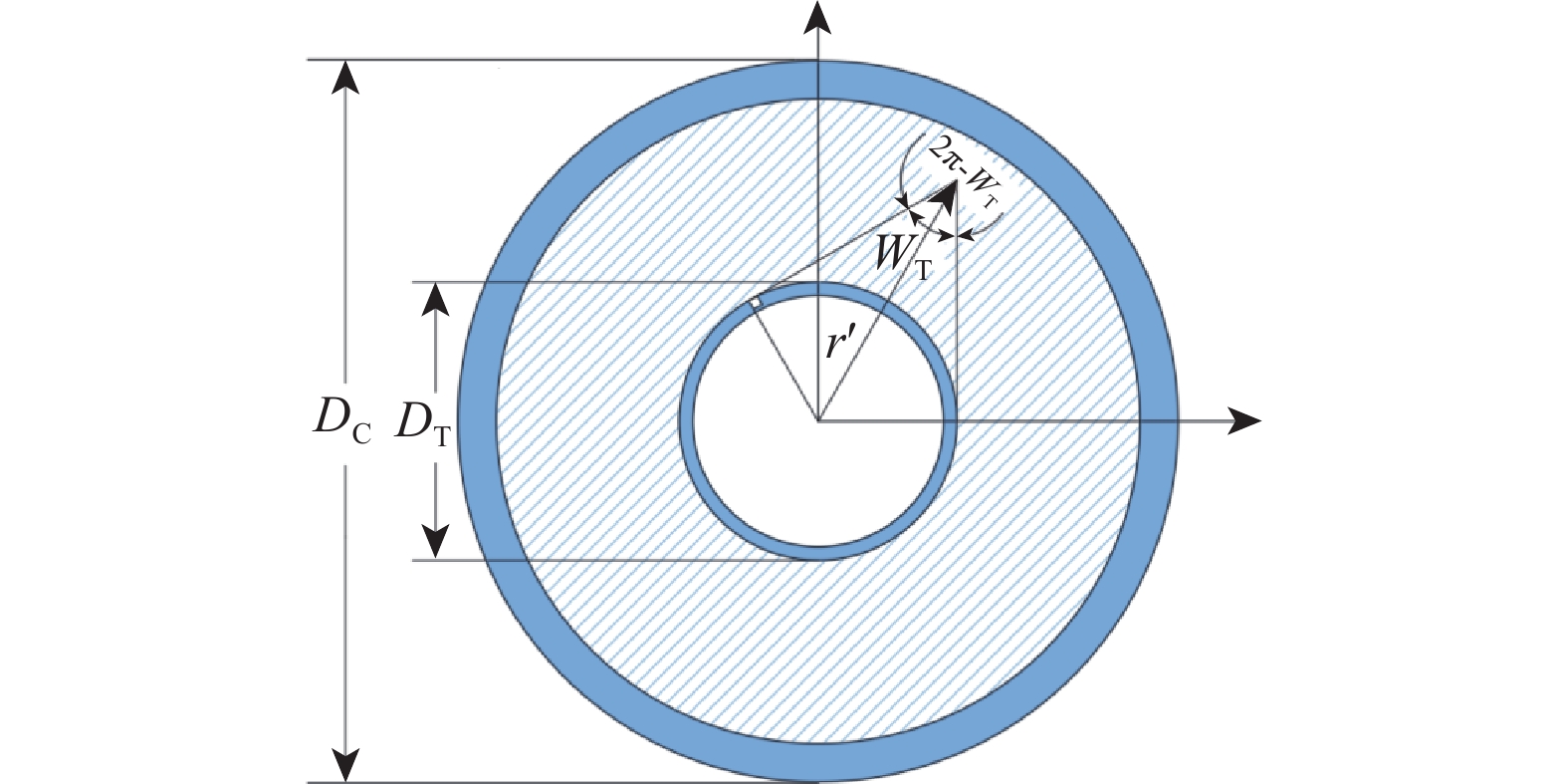
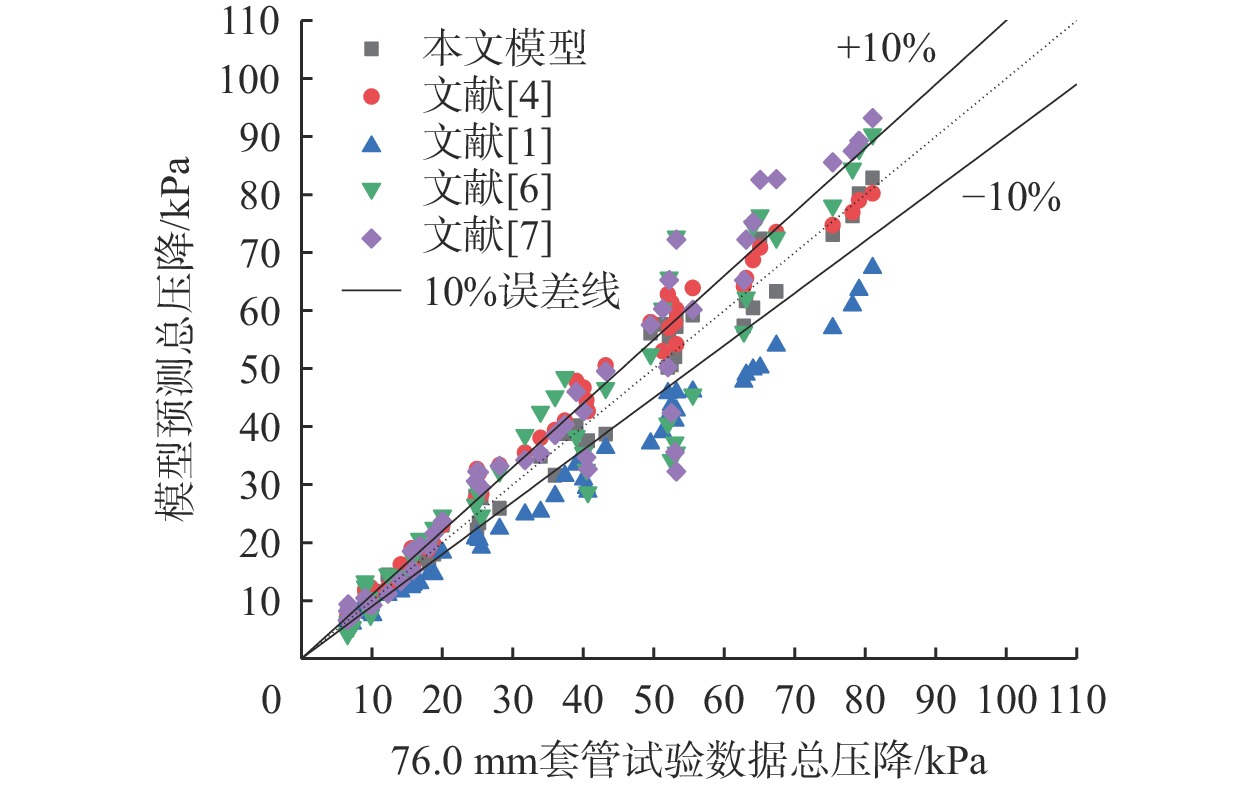
针对高气液比环空多相流试验研究不充分且压降预测精度不高的问题，以水和空气为试验介质，选择2种油套管组合（油管外径和套管内径分别为38.5 mm×62.0 mm、38.5 mm×76.0 mm），在长11.5 m的测试管内开展试验研究。试验发现，对于垂直向上的环状流，随着气液表观流速增大，总压降增大，且总压降增长幅度随着气相速度增大而一直增大；气液表观流速相同时，管道的截面积越小，摩阻压降越大。考虑环空环状流内外管两层液膜流速的差异，基于文献[1]建立了环空环状流压降计算方法，计算了液膜与管壁及液膜与气芯之间的摩阻系数；结合液膜和气芯之间的动量平衡条件，利用文献[4]给出的内外管液膜厚度比相关式，建立了新的环空环状流压降预测模型。用试验数据对新模型和现有模型进行了对比验证，结果表明，新模型预测误差小于10%，结果较为可靠，可为油套环空压力预测、气举管柱设计及油井生产工况分析等提供理论基础。
Abstract:In view of insufficient experimental research on annular multiphase flow tests with high gas-liquid ratios and low prediction accuracy of pressure drop, water and air were selected as the experimental media, and the two different combinations of oil tube and casing (The outer diameter of the oil tube and the inner diameter of the casing were 38.5 mm × 62.0 mm and 38.5 mm × 76.0 mm, respectively) were selected. Moreover, experimental studies were carried out in an 11.5 m long test tube. The experimental results show that the total pressure drop increases with the increase as the apparent gas-liquid flow rate increases for vertically upward annular flow. The increase in the total pressure drop accelerates as the gas flow rate rises. At the same apparent gas-liquid flow rate, the friction pressure drop of the tube with a smaller cross-sectional area is larger. Based on the pressure drop calculation method for annular flow in the annular space established in the literature [1], the flow rate difference between liquid films of annular flow in the annular space inside and outside the tube is considered in calculating the friction coefficient between liquid film and tube wall and between liquid film and gas core. According to the momentum balance condition between the liquid film and the gas core, the thickness ratio equation for liquid films inside and outside the tube given by literature [4] is employed. The new pressure drop prediction model for annular flow in the annular space is developed and compared with the existing model for verification based on the experimental data. The results show that the calculation error of the new model is less than 10%, and the prediction results are reliable, which can provide a theoretical basis for the prediction of annular pressure in oil tubes and casing, gas lift design, and the analysis of oil well production conditions.
-
西湖凹陷位于东海陆架盆地浙东坳陷东部，面积约5.9×104 km2，新生代地层最大沉积厚度超过1.0×104 m，主要目的层为古近系平湖组和花港组地层。储层岩性以长石砂岩和岩屑砂岩为主，埋深一般大于3 500.00 m，受压实成岩作用影响，储层物性一般偏低，孔隙度多在15%以下，渗透率一般小于10 mD。低孔低渗储层的流体性质识别一直是西湖凹陷油气勘探开发中的难题之一[1–3]，原因是储层束缚水含量高、电阻率对比度低，同时受储层孔隙结构影响，水层的电阻率往往也较高，通过电性判别难度较大[4–6]；另外，低孔低渗储层毛细管水含量高，当生产压差增大到一定数值后，一部分束缚水往往会转化为可动水，导致生产出水，影响油气产量，特别是气层一旦出水将严重影响最终的采收率，降低油气田开发的经济性[7–10]。针对上述问题，笔者利用油基钻井液的高侵特性，基于时移测井理念[11–12]，提出时移电阻率测井对比识别法，即通过对比随钻实时电阻率与复测电阻率的差异快速识别流体性质，并在西湖凹陷低孔低渗储层进行了现场应用，验证了其可行性和有效性。
1. 油基钻井液滤失性试验
西湖凹陷低孔低渗储层钻井使用的油基钻井液主要成分为白油，根据实际需要，其含量约占钻井液总体积的70%～85%，其余成分为水和各种添加剂，主要起乳化、降滤失和封堵作用。虽然油基钻井液比水基钻井液具有更好的井壁稳定和储层保护作用，但仍具有一定的侵入特性。为了分析油基钻井液的滤失特征，利用具有低孔低渗特征的人造岩心进行了滤失性试验，岩心参数见表1。
表 1 油基钻井液滤失性试验所用岩心的主要参数Table 1. Core parameters of oil-based drilling fluid filtration test编号 长度/cm 直径/cm 渗透率/mD 钻井液密度/（kg·L–1） 1 7.39 2.49 199 1.18 2 7.34 2.53 198 1.32 将岩心放入夹持器内，逐渐加压至13 MPa，并持续24 h，测量滤失量、滤饼厚度和滤液侵入深度。试验结果为：1号岩心滤饼厚4.0 mm，滤液侵入深度为 3.5 cm；2号岩心滤饼厚5.0 mm；滤液侵入深度为6.5 cm；滤失量与侵入时间的关系如图1所示。
![]()
图 1 油基钻井液滤失量与侵入时间的关系Figure 1. Relationship between fluid loss and intrusion time of oil-based drilling fluid从图1可以看出，油基钻井液存在一定的滤失性，滤液能够侵入岩心，滤失量与岩心物性、压差和时间都有一定的关系。这是因为，油基钻井液滤液侵入地层后，会对储层中原有流体产生一定的驱替作用，导致储层电性特征变化，所以可通过对比储层电性特征变化情况分析判断储层流体的性质。
2. 时移电阻率测井对比识别法原理
地层刚钻开时，油基钻井液滤液侵入量小，滤饼薄，冲洗带和过渡带较窄；钻开一段时间后，滤饼增厚，冲洗带和过渡带宽度增大[13]，如图2所示。所以，刚钻开地层进行随钻电阻率测井时，该电阻率一般可以代表地层真电阻率，即原状地层电阻率Rt；地层钻开一段时间后复测电阻率时，电阻率特别是探测深度较浅的电阻率（Rs）会包含冲洗带和过渡带的流体性质变化信息。对于水基钻井液，Rs相对于Rt增大或减小，取决于钻井液滤液矿化度和地层水矿化度的相对大小关系；但对于油基钻井液，由于钻井液滤液不导电，当地层水被驱替后，复测时电阻率Rs会变大，即复测Rs大于随钻测量Rs。时移电阻率测井对比识别法就是利用含有不同性质流体的储层被油基钻井液滤液驱替后、表现出不同的电性变化特征进行流体识别。
![]()
图 2 地层刚钻开和钻开一段时间后的井筒环境Figure 2. Wellbore environments after penetrating the formation soon and drilling for a while为了进一步说明时移电阻率测井对比识别法的技术原理，分别分析了探测深度与被探测地层电阻率的关系，以及油基钻井液滤液侵入不同地层后的电阻率变化特征。
首先用Schlumberger公司的ARC随钻电阻率测井仪（以下简称ARC测井仪）分析探测深度与被探测地层电阻率的关系。该仪器有5个源距（406.4，558.8，711.2，863.6和1 016.0 mm）的发射器，采用2种发射频率（400 kHz和2 MHz），所以可以获得20条电阻率曲线（10条相位电阻率和10条衰减电阻率）。其中，发射频率为2 MHz时，ARC测井仪探测深度与地层相位电阻率的关系曲线如图3所示。
![]()
图 3 P16H探测深度与被探测地层电阻率的关系曲线Figure 3. Relationship curve between P16H detection depth and the resistivity of measured formation由图3可知，P16H（源距为406.4 mm，频率为2 MHz的相位电阻率）探测深度最小，但其探测深度与地层电阻率相关，电阻率越高，探测深度越大。由于油基钻井液滤液侵入深度小，所以可以利用P16H电阻率的变化率分析侵入深度。
然后分析油基钻井液滤液分别侵入油气层、水层、含油气水层和干层后，冲洗带电阻率的变化情况。对于油气层，油气和油基钻井液滤液都是不导电的流体介质，油基滤液侵入地层后，地层电阻率基本不变；对于水层、含油气水层或同层，油基钻井液滤液侵入后会减小导电流体（水）的体积，导致储层的电阻率升高。实际复测时，同时测量砂岩储层及上下泥质围岩的电阻率，由于泥岩为非渗透性层，所以随钻实时电阻率和复测电阻率保持一致，通过使围岩电阻率重合，就可以确定砂岩储层电阻率的变化。钻井液滤液的侵入深度与储层物性、井筒过平衡压差、侵入时间及钻井液特性都有关系。例如，西湖凹陷某区域的典型低孔低渗储层，孔隙度为9%～18%，渗透率为1～50 mD，在较大正压差和较长完钻时间下的侵入深度一般较大。而致密层由于储层物性太差，滤液基本无侵入，所以地层电阻率基本不变。不同地层的具体变化特征见表2（其中，P16H实时，指P16H随钻实时电阻率；P16H复测，指P16H复测电阻率）。
表 2 油基钻井液滤液侵入不同地层后的电阻率变化特征Table 2. Characteristics of resistivity change after oil-based drilling fluid filtrate invaded different formations地层类型 钻井液滤液侵入情况 电阻率变化情况 ARC测井仪测量结果 油气层 一定压差下侵入 不变 P16H实时≈P16H复测 水层 一定压差下侵入 升高 P16H实时<P16H复测 含油气水层或同层 一定压差下侵入 升高 P16H实时<P16H复测 致密层 基本无侵入 不变 P16H实时≈P16H复测 3. 现场应用
时移电阻率测井对比识别法在西湖凹陷X1井和X2井进行了应用，均取得了成功，证明该方法可行且有效。
X1井4 450.00～4 475.00 m井段钻遇油气显示层，电阻率最高50 Ω·m，气测全量Tg最高12.0%，岩性为长石细砂岩，孔隙度为9%～11%，渗透率为1～5 mD，参照邻井信息，初步判断该层为气层。对该层进行了随钻电阻率复测，结果如图4所示。图4中，第五道“电阻率对比”指P16H随钻实时电阻率（P16H实时）与P16H复测电阻率（P16H 复测）的对比；P16H复测值大于P16H实时值（对应部分进行了蓝色充填），表明该层为非纯气层，存在一定量的可动水，或者说在该井钻井液过平衡压差约6.9 MPa的条件下，储层孔隙中的部分水可以流动。
![]()
图 4 X1井随钻电阻率实时值与复测值的对比Figure 4. Comparison on the resistivity while drilling real-time measurement and the re-tested value in Well X1X1井完钻后，在井深4 471.50 m处进行了电缆地层测试泵抽取样（MDT仪器），泵抽至45 min时，通过井下流体识别仪IFA开始观察到地层天然气流体，流线中的成分主要为天然气和油基钻井液；泵抽至160 min时，泵抽压差增大至4.13 MPa，流线出现了明显的地层水信号，说明在该压差下一部分毛细管水开始流动，转变为可动水。泵抽结束时，流线中水的体积比约为17%，该结果与电阻率复测分析结果完全一致（如图5所示）。这说明该层有一部分毛细管水在压差大于4.13 MPa时是可以流动的，可以称这部分水为弱束缚水；后续进行地层测试或开发时，生产压差应小于4.13 MPa，否则会导致地层出水，影响天然气产能。
![]()
图 5 X1井井深4 471.50 m MDT泵抽流体性质综合识别Figure 5. Comprehensive identification of 4 471.50 m MDT pumping fluids properties in Well X1X2井与X1井处于同一构造带，应用油基钻井液钻进。该井4 317.00～4 336.00 m井段钻遇油气显示层，岩性为长石细砂岩，孔隙度为10%～15%，渗透率为1～10 mD。储层上部电阻率约24 Ω·m，气测全量Tg最高约6.0%；储层下部电阻率为13 Ω·m，气测全量Tg约为2.8%。与邻区同层位油气层相比，该层整体电阻率较低，认为该层未达到纯油气层的标准，为此进行了电阻率随钻与复测对比，结果如图6所示。该井钻井液过平衡压差为7.13 MPa。图6中，第五道为P16H实时值和复测值的对比结果，可以看出井深4 330.00 m以浅的P16H实时值与P16H复测值一致，说明该层不含可动水，为纯油气层；井深4 330.00 m以深的P16H复测值明显大于P16H实时值，说明该层含可动水，推测为气水同层。
![]()
图 6 X2井随钻电阻率实时值与复测值的对比Figure 6. Comparison on the resistivity while drilling real-time measurement and the re-tested value in Well X2完钻后，X2井在井深4 321.20和4 333.00 m处分别进行了MDT泵抽取样。井深4 321.20 m处泵抽压差约13.8 MPa，泵抽时间为115 min，证实为纯轻质油层，不含水；井深4 333.00 m处泵抽压差为18.3 MPa，泵抽时间为120 min，后期含水率为60%，证实为油水同层，流体性质识别具体情况如图7所示。该井的泵抽结果与电阻率复测对比分析结果完全一致，再次证明了该方法的可行性和有效性。
![]()
图 7 X2井井深4 321.20和4 333.00 m MDT泵抽流体性质综合识别Figure 7. Comprehensive identification of MDT pumping fluid properties at 4 321.20 and 4 333.00 m in Well X24. 结论与建议
1）油基钻井液滤液侵入地层后，对储层中原有流体有一定驱替作用，从而引起储层电性特征的变化，通过对比该变化情况，就能够对储层中原有流体性质进行分析判断。
2）低孔低渗储层岩性和孔隙结构复杂，仅仅依靠对比电阻率的高低或者邻区经验识别流体的性质很难得到准确的结果。油基钻井液条件下利用时移电阻率测井对比识别法，可以快速识别低孔低渗储层的流体性质，现场应用也验证了该方法具有较高的准确性。
3）时移电阻率测井对比识别法具有较好的通用性，只要使用随钻电阻率和油基钻井液均可进行借鉴，特别是对于一些新区探井，该方法能够快速识别流体性质，为后续作业选择提供指导，提高作业效率并节省成本。
-
![]()
图 1 环空气液两相流试验装置及试验流程
1.空气压缩机；2.阀门；3.储气罐；4.流量计；5.混合器；6.快关阀；7.压力传感器；8.温度传感器；9.高速摄像机；10.压差传感器；11.数据采集系统；12.外管；13.内管；14.气液分离器；15.油水混合罐；16.水泵
Figure 1. Experimental setup and process of gas-liquid two-phase flow in annular space
![]()
图 2 ϕ38.5 mm×ϕ62.0 mm油套环空环状流
Figure 2. Annular flow in annular space of ϕ38.5 mm×ϕ62.0 mm
![]()
图 3 ϕ38.5 mm×ϕ76.0 mm油套环空环状流
Figure 3. Annular flow in annular space of oil tube and casing of ϕ38.5 mm ×ϕ76.0 mm
![]()
图 4 ϕ38.5 mm×ϕ62.0 mm环空不同气体表观流速下环状流的总压降
Figure 4. Total pressure drop of annular flow in a ϕ38.5 mm×ϕ62.0 mm annulus at different gas apparent velocity
![]()
图 5 ϕ38.5 mm×ϕ76.0 mm环空不同气体表观流速下环状流的总压降
Figure 5. Total pressure drop of annular flow in a ϕ38.5 mm×ϕ76.0 mm annulus at different gas apparent velocity
![]()
图 6 ϕ38.5mm×ϕ62.0 mm、ϕ38.5 mm×ϕ76.0 mm两种环空的总压降
Figure 6. Total pressure drop in two annulus types: ϕ38.5mm×ϕ62.0 mm and ϕ38.5 mm×ϕ76.0 mm
![]()
图 7 垂直同心环形环状流液膜理想结构
Figure 7. Ideal structure of liquid film of vertical concentric annular flow
![]()
图 10 ϕ62.0 mm外管压降模型预测结果与试验结果对比
Figure 10. Comparison between predicted results of pressure drop model of ϕ62.0 mm outer tube and experimental results
![]()
图 11 ϕ76.0 mm外管压降模型计算结果与试验结果对比
Figure 11. Comparison between predicted results of pressure drop model of ϕ76.0 mm outer tube and experimental results
表 1 流体物理参数（25 ℃）
Table 1 Physical parameters of fluids (25 ℃)
相 密度/（kg∙m−3） 动力黏度/
（mPa∙s）空气−水表面张力/
（mN∙m−1）空气 1.1691 0.018 60 72.5 水 997.05 0.890 08 
下载: 导出CSV
表 2 试验数据
Table 2 Experimental data
环空尺寸 角度/
（°）液体表观流速/
（m∙s−1）气体表观流速/
（m∙s−1）试验
组数ϕ38.5 mm×ϕ62.0 mm 90 0.074 9～ 0.624 5 20～200 56 ϕ38.5 mm×ϕ76.0 mm 90 0.041 2～1.033 4 20～200 70
下载: 导出CSV
-
[1] 张军,陈听宽,闻建龙,等. 垂直同心环形管内上升气液两相环状流含气率与压降预测[J]. 化工学报,2003,54(1):47–51. doi: 10.3321/j.issn:0438-1157.2003.01.011 ZHANG Jun, CHEN Tingkuan, WEN Jianlong, et al. Prediction of void fraction and pressure drop for upward gas-liquid two-phase flow through vertical concentric annulus[J]. CIESC Journal, 2003, 54(1): 47–51. doi: 10.3321/j.issn:0438-1157.2003.01.011
[2] 尹邦堂,李相方,孙宝江,等. 井筒环空稳态多相流水动力学模型[J]. 石油勘探与开发,2014,41(3):359–366. doi: 10.11698/PED.2014.03.13 YIN Bangtang, LI Xiangfang, SUN Baojiang, et al. Hydraulic model of steady state multiphase flow in wellbore annuli[J]. Petroleum Exploration and Development, 2014, 41(3): 359–366. doi: 10.11698/PED.2014.03.13
[3] 吴绍伟. 垂直环空气液两相流理论及在油井生产中的应用[D]. 青岛:中国石油大学(华东),2009. WU Shaowei. Theoretical investigation of upward gas-liquid two-phase flow in annuli and applications in the process of production in oilfield[D]. Qingdao: China University of Petroleum(East China), 2009.
[4] CAETANO E F, SHOHAM O, BRILL J P. Upward vertical two-phase flow through an annulus: part II: modeling bubble, slug, and annular flow[J]. Journal of Energy Resources Technology, 1992, 114(1): 14–30. doi: 10.1115/1.2905916
[5] SADATOMI M, SARUWATARI S, SATO Y. Two-phase flow in vertical noncircular channels[J]. Transactions of the Japan Society of Mechanical Engineers Series B, 1982, 48(434): 1893–1900. doi: 10.1299/kikaib.48.1893
[6] LAGE A C V M, TIME R W. An experimental and theoretical investigation of upward two-phase flow in annuli[J]. SPE Journal, 2002, 7(3): 325–336. doi: 10.2118/79512-PA
[7] KELESSIDIS V C, DUKLER A E. Modeling flow pattern transitions for upward gas-liquid flow in vertical concentric and eccentric annuli[J]. International Journal of Multiphase Flow, 1989, 15(2): 173–191. doi: 10.1016/0301-9322(89)90069-4
[8] WALLIS G B. One-dimensional two-phase flow[M]. New York: McGraw-Hill, 1969: 896-1105.
[9] HASAN A R, KABIR C S. Two-phase flow in vertical and inclined annuli[J]. International Journal of Multiphase Flow, 1992, 18(2): 279–293. doi: 10.1016/0301-9322(92)90089-Y
[10] IBARRA R, NOSSEN J, TUTKUN M. Two-phase gas-liquid flow in concentric and fully eccentric annuli: part II: model development, flow regime transition algorithm and pressure gradient[J]. Chemical Engineering Science, 2019, 203: 501–510. doi: 10.1016/j.ces.2019.02.021
[11] TATTERSON D F, DALLMAN J C, HANRATTY T J. Drop sizes in annular gas-liquid flows[J]. AIChE Journal, 1977, 23(1): 68–76. doi: 10.1002/aic.690230112
[12] 刘杨,李维仲. 垂直上升气液环状流流动参数的数值计算[J]. 计算力学学报,2011,28(1):96–101. doi: 10.7511/jslx201101018 LIU Yang, LI Weizhong. Numerical simulation on vertical upward gas-liquid annular flow[J]. Chinese Journal of Computational Mechanics, 2011, 28(1): 96–101. doi: 10.7511/jslx201101018
[13] 熊至宜,张云,张丽稳,等. 煤层气井筒气液两相流数值模拟[J]. 中国石油大学学报(自然科学版),2023,47(2):153–159. doi: 10.3969/j.issn.1673-5005.2023.02.018 XIONG Zhiyi, ZHANG Yun, ZHANG Liwen, et al. Numerical simulation on gas-liquid two-phase fluid in coal-bed methane wellbore[J]. Journal of China University of Petroleum(Edition of Natural Science), 2023, 47(2): 153–159. doi: 10.3969/j.issn.1673-5005.2023.02.018
[14] 张绪亮,张驰,周波,等. 深井大尺寸环空气液两相流动规律数值模拟研究[J]. 石油钻探技术,2024,52(6):37–49. ZHANG Xuliang, ZHANG Chi, ZHOU Bo, et al. Numerical simulation of gas-liquid two-phase flow pattern in large annulus of deep well[J]. Petroleum Drilling Techniques, 2024, 52(6): 37–49.
[15] XIAO J J, SHONHAM O, BRILL J P. A comprehensive mechanistic model for two-phase flow in pipelines[R]. SPE 20631, 1990.
[16] 刘通,王世泽,郭新江,等. 气井井筒气液两相环雾流压降计算新方法[J]. 石油钻采工艺,2017,39(3):328–333. LIU Tong, WANG Shize, GUO Xinjiang, et al. New calculation method of gas-liquid two phase annular-mist flow pressure drop of wellbores in gas wells[J]. Oil Drilling & Production Technology, 2017, 39(3): 328–333.
[17] FORE L B, BEUS S G, BAUER R C. Interfacial friction in gas–liquid annular flow: analogies to full and transition roughness[J]. International Journal of Multiphase Flow, 2000, 26(11): 1755–1769. doi: 10.1016/S0301-9322(99)00114-7
[18] Jonsson V K, Sparrow E M . Experiments on turbulent-flow phenomena in eccentric annular ducts[J]. Journal of Fluid Mechanics, 1966, 25(1): 65–86. doi: 10.1017/S0022112066000053
[19] 毛伟,张绍槐,梁政. 垂直向上环状流特性参数预测模型[J]. 钻采工艺,2000,23(2):25–28. doi: 10.3969/j.issn.1006-768X.2000.02.008 MAO Wei, ZHANG Shaohuai, LIANG Zheng. A predicting model for upward annular flow properties in vertical gas well[J]. Drilling & Production Technology, 2000, 23(2): 25–28. doi: 10.3969/j.issn.1006-768X.2000.02.008
[20] HEWITT G F, WHALLEY P B. The correlation of liquid entrainment fraction and entrainment rate in annular two-phase flow[R]. AERE-R9187, 1978.
[21] HENSTOCK W H, HANRATTY T J. The interfacial drag and the height of the wall layer in annular flows[J]. AIChE Journal, 1976, 22(6): 990–1000. doi: 10.1002/aic.690220607
-
期刊类型引用(6)
1. 张浩，倪利平，罗刚，王雪亮，王亮. 油基钻井液侵入对核磁共振测井响应影响的实验研究. 科学技术与工程. 2023(12): 5013-5021 . 
百度学术
2. 罗健，张国栋，胡文亮，魏晓晗，何玉春. 低渗储层泥浆侵入特征与时移电阻率测井评价. 海洋石油. 2022(02): 55-60+76 . 百度学术
3. 吴进波，陈鸣，孙殿强，王锋，周基恒. 随钻地层测试在大斜度井油基钻井液中的应用. 石油钻采工艺. 2022(02): 178-185 . 百度学术
4. 张志强，王猛，杨杰. 油基泥浆环境下储层电阻率动态剖面反演方法研究及应用. 石化技术. 2021(06): 116-117 . 百度学术
5. 李新，米金泰，张卫，姚金志，李三国. 井下随钻核磁共振流体分析装置设计与试验验证. 石油钻探技术. 2020(02): 130-134 . 本站查看
6. 邱小雪，戴家才，陈猛，程伊博. 基于VOF对低产积液气井流动特征的数值模拟. 断块油气田. 2020(05): 619-623 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 28
- HTML全文浏览量: 7
- PDF下载量: 11
- 被引次数: 8
