随着油气勘探开发向高温高压地层、窄安全密度窗口地层、复杂压力地层钻进，溢流频繁发生，一旦检测不及时，极易引发井喷，甚至可能发生人员伤亡等重大钻井事故^[1–7]，开展溢流早期检测方法研究对于保障钻井安全具有重要作用。传统溢流检测方法主要分析综合录井仪实时获取的钻井液池液位、出入口流量和钻井液密度等参数的变化情况^[8–13]，严重依赖经验，可靠性和及时性难以保证。近年来，国内外学者利用随机森林、Bi-GRU和人工神经网络，建立了溢流智能检测模型^[14–16]，虽然可自动提取溢流与钻井参数之间的关系，但未考虑溢流数据稀缺和不同井之间钻井参数的差异，均无法取得良好的泛化效果。为此，学者们通过提取钻井参数序列波动趋势，结合阈值法和加权法，构建了相关的溢流早期智能识别方法^[17–20]。此类方法不依赖大量的溢流数据，且受钻井参数差异影响较小，但未充分考虑不同钻井工况下特征参数的差异、钻井工况对特征参数波动趋势的影响及特征参数在溢流不同阶段的响应差异，无法满足超深井钻井全过程预警的准确性和时效性。

为此，笔者基于随机森林算法建立钻井工况智能识别模型，提出总池液面高度、出口流量和立管压力等特征参数的序列波动趋势提取方法，融合多参数波动趋势，建立溢流风险指数自适应计算方法，以实现钻井全过程中溢流早期智能检测，为保障钻井安全提供技术支持。

1.   钻井工况智能识别模型

钻井工况可以划分为静止、原地循环、原地旋转、原地循环（旋转）、起钻、起钻（开泵）、倒划眼、干倒划眼、下钻、下钻（开泵）、划眼、干划眼、复合钻进和滑动钻进等14种类别，不同钻井工况下溢流特征参数及其响应规律如表1所示。不同钻井工况下溢流特征参数及其响应规律不同，例如静止、起下钻工况下井筒内没有钻井液循环，立管压力不能作为检测溢流的关键特征参数；而复合钻进、滑动钻进工况下立管压力是检测溢流的关键特征参数。对此，需建立钻井工况智能识别模型，指导特征参数实时优选。

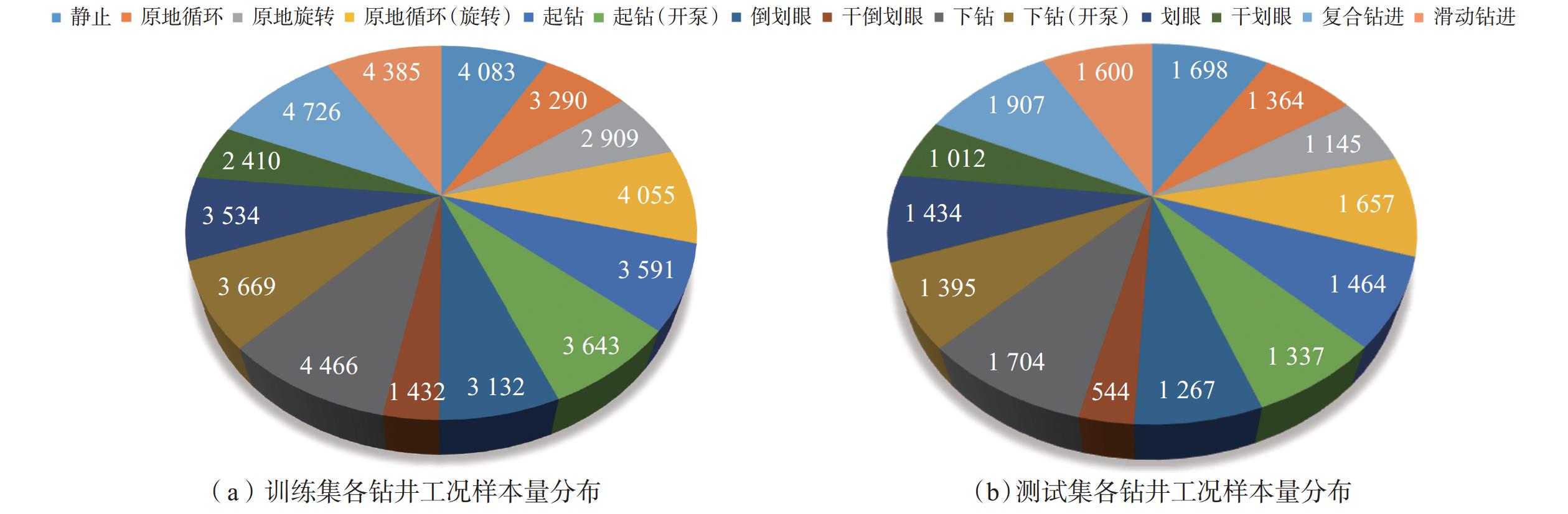
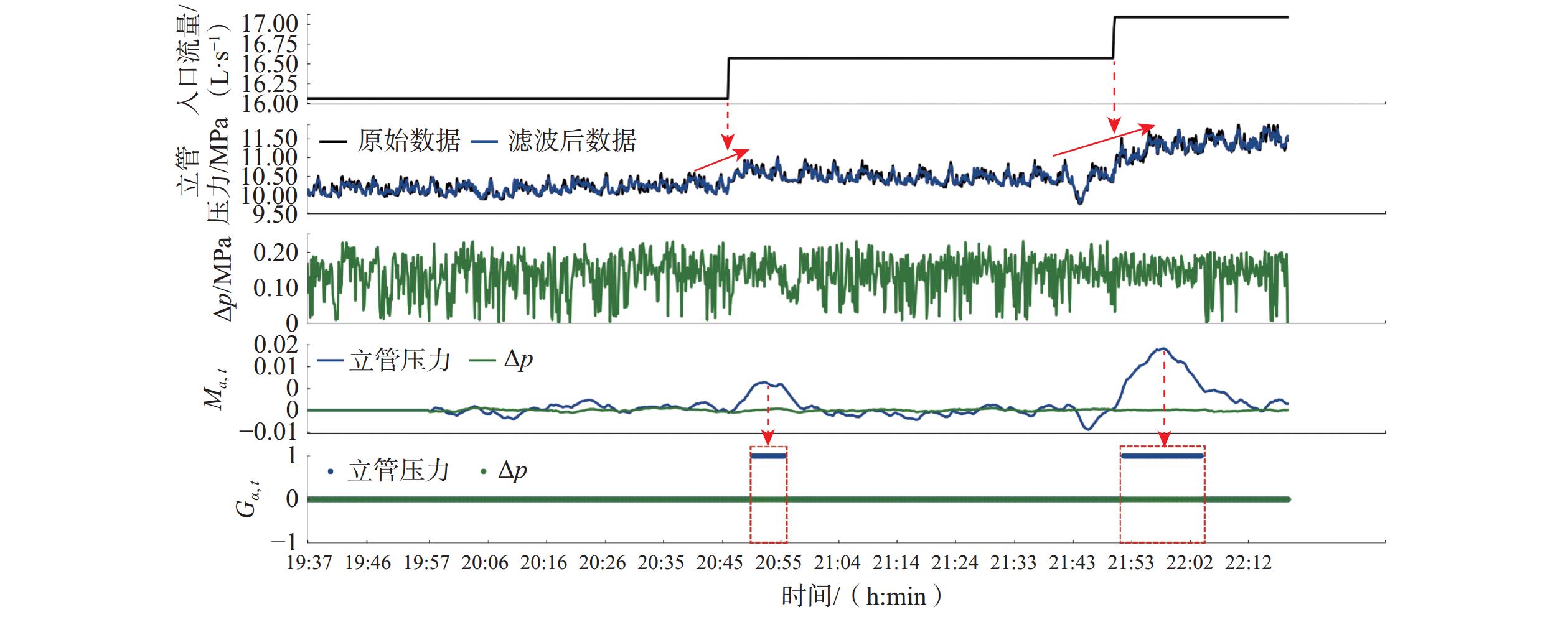
表  1  不同钻井工况下发生溢流时特征参数及其响应规律

Table  1.  Characteristic parameters and response rules of kick under different drilling conditions

钻井工况	溢流特征参数	响应规律
静止、原地旋转	出口流量、总池液面高度	井口有钻井液流出，总池液面升高
原地循环、原地循环（旋转）、复合钻进、滑动钻进	出口流量、总池液面高度、 立管压力、出口密度	入口流量大于出口流量，总池液面升高，立管压力和出口密度降低
起钻、干倒划眼	总池液面高度	钻井液灌入量小于起出钻具体积
起钻（开泵）、倒划眼	出口流量和密度、总池液面高度	出口流量大于入口流量，钻井液注入量小于起出钻具体积，出口密度降低
下钻、干划眼	总池液面高度	钻井液返出量大于下入钻具体积
下钻（开泵）、划眼	出口流量和密度、总池液面高度	出口流量大于入口流量，钻井液返出量大于下入钻具体积，出口密度降低

下载: 导出CSV 

| 显示表格

1.1   钻井参数分析

由于现场复杂环境对传感器测量精度的干扰，录井参数实测值与理论阈值存在差异。随机森林算法能够基于大量录井数据自动提取钻井工况与录井参数间的映射关系，确定各参数阈值，并以树状图的形式清晰呈现出钻井工况识别规则，具有可解释性强的优势^[21–22]。钻井工况与录井参数间的映射关系可以表示为：

式中：y为钻井工况类别；H_t为t时刻的井深，m；H_b,t为t时刻的钻头位置，m；p_t为t时刻的钻压，kN；T_t为t时刻的扭矩，kN·m；n_t为t时刻转盘的转速，r/min；Q_t为t时刻入口流量，L/s；p_sp,t为t时刻立管压力，MPa；D_t为钻进趋势，m。

1.2   数据样本收集

采用某油田现场10口井的录井数据，选择其中7口井为训练集，3口井为测试集。结合钻井日志和专家经验，最终得到训练集和测试集中各钻井工况样本总量如图1所示。

图  1  训练集与测试集各钻井工况样本量分布

Figure  1.  Sample size distribution for each drilling condition in training set and test set

下载: 全尺寸图片 幻灯片

1.3   模型训练与解释

逻辑森林算法中，决策树的数量越多，模型的泛化性越强，计算成本也会随之增加。树深度越大，模型的拟合能力约强，但可能会造成过拟合。为保证模型的泛化性，结合网格搜索和5折交叉验证来确定其最优值，结果如图2所示。树深度从1增加至6时，模型准确率也逐渐增大并达到峰值；对应决策树数量大于45时，模型准确率保持不变。因此，最终确定决策树数量为45，树深度为6，使用Python编程语言中的sklearn库进行训练。

图  2  不同决策树数量和树深度组合下模型的准确率

Figure  2.  Model accuracy under different combinations of decision tree number and tree depth

下载: 全尺寸图片 幻灯片

模型训练完成后，随机对其中一棵决策树进行可视化，并以倒划眼工况识别过程为例，对该模型可解释性进行剖析，其他工况识别过程与倒划眼工况类似，由于图像大小的限制，用$(\cdots )$表示相应节点后的分支过程（见图3）。起钻过程中上提钻具遇卡时，通常需要进行倒划眼，主要特征为钻头位置变浅，存在转盘转速、入口流量和立管压力。红色箭头表示模型识别倒划眼工况的过程，首先根据t时刻入口流量判断是否开泵循环，然后根据t时刻钻进趋势判断钻具是否上提，最后根据t时刻转盘转速实现倒划眼识别，该过程与专家经验吻合。

图  3  钻井工况智能识别模型可视化结果

Figure  3.  Visualization results of intelligent recognition model for drilling conditions

下载: 全尺寸图片 幻灯片

1.4   模型测试

钻井工况智能识别模型在测试集上的识别准确率如图4所示。由图4可以看出，各工况平均准确率为96.5%，其中复合钻进准确率最高为99%，说明该模型在新样本中有很好的泛化性。

图  4  钻井工况智能识别模型测试结果

0.下钻；1.下钻（开泵）；2.划眼；3.干划眼；4.起钻；5.起钻（开泵）；6.倒划眼；7.干倒划眼；8.原地旋转；9.原地循环；10.原地循环（旋转）；11.静止；12.复合钻进；13.滑动钻进

Figure  4.  Test results of intelligent recognition model for drilling conditions

下载: 全尺寸图片 幻灯片

2.   溢流早期智能检测方法

实时获取当前钻井工况类型后，基于工程参数变化趋势溢流早期智能检测方法的流程主要包括溢流特征参数预处理、特征参数序列趋势提取和溢流风险指数自适应计算，如图5所示。

图  5  溢流早期智能检测的流程

Figure  5.  Flow chart of early intelligent kick detection

下载: 全尺寸图片 幻灯片

2.1   溢流特征参数预处理

实时测量的特征参数可能包含一定的扰动，影响趋势值的准确计算。为此，使用5层小波分解与重构算法对溢流特征参数进行平滑处理。

对于起下钻、划眼和倒划眼等与上提/下放钻具有关的钻井工况，在提取序列趋势前，需要对总池液面高度进行校正，使其能够真实反映溢流复杂工况。如下钻过程中，钻具下放会排出井筒中的部分钻井液，使总池液面升高。对此，若钻井工况智能识别模型识别结果为起钻、干倒划眼、起钻（开泵）、倒划眼时，基于式（2）对总池钻井液体积进行校正；若识别结果为下钻、干划眼、下钻（开泵）、划眼时，基于式（3）对总池钻井液体积进行校正。

式中：V'为校正后总池钻井液体积，m³；V为总池钻井液体积测量值，m³；h为起出/下放钻具高度，m；d₁为钻杆外径，m；d₂为钻杆内径，m。

循环、复合钻进和滑动钻进等钻井工况与钻井液循环有关，立管压力为检测溢流的关键参数。但若人为改变钻井液入口流量，会使立管压力在非溢流情况下发生较大波动，造成误报和漏报。立管压力主要由管柱内压耗、钻头压耗和环空压耗组成^[23–24]。

层流时，管柱内压耗可表示为：

紊流时，可表示为：

式中：p₁为管柱内压耗，Pa；μ为有效黏度，Pa·s；n为流性指数；ρ为钻井液密度，kg/m³；v_p为管柱内钻井液流速，m/s；L为管道长度，m。

钻头压耗可表示为：

式中：p₂为钻头压耗，MPa；Q为钻井液流量，L/s；A₀为喷嘴出口截面积，cm²。

层流时，环空压耗可表示为：

紊流时，可表示为：

式中：p₃为环空压耗，Pa；v_a为环空内钻井液流速，m/s；d_w为井眼直径，m。

为减弱人为因素对立管压力序列变化趋势的影响，使用测量值与计算值的差值替换立管压力：

式中：Δp为立管压力测量值与计算值的差值，MPa；p_spm为实测立管压力，MPa。

同理，钻井液出口密度与入口密度密切相关，使用出入口密度差替换出口密度：

式中：Δρ为出入口密度差，kg/L；ρ_in为钻井液入口密度，kg/L；ρ_out为钻井液出口密度，kg/L。

2.2   特征参数序列趋势提取方法

使用一元线性回归方程中的斜率表示其变化趋势，若斜率大于0，表明序列呈上升趋势，反之，则呈下降趋势。考虑特征参数局部波动对整体趋势的影响，构建了特征参数序列趋势值计算方法。

式中：M_α,t为t时刻长度为α的特征参数序列趋势值；w_i,α为子序列（数据点i到α）的权重，且满足i越接近α时，w_i,α越小；k_i,α为子序列的斜率。

钻井液出口流量序列趋势值与入口流量序列趋势值密切相关。钻井液入口流量指单位时间内流入井口的钻井液体积，出口流量为钻井液返出井口时在架空槽或缓冲罐内的钻井液面的相对变化量，两者单位不同，无法使用流量差来减弱这一影响，需要校正流量序列趋势。

式中：M_α,t,1为t时刻出口流量序列趋势值；M_α,t,2为t时刻入口流量序列趋势值；α为特征参数序列窗口大小；β为入口流量序列趋势阈值。

为了计算溢流风险指数，将提取的趋势值分为3个等级，1表示增加，0表示不变，−1表示减小。

式中：G_α,t为趋势值划分等级结果；δ为特征参数序列趋势阈值，其值越小，对溢流特征参数的细微变化越敏感。

循环工况下立管压力序列趋势提取结果如图6所示，该时间段内无溢流发生，其中α=60，δ=0.005，数据采样间隔为10 s。从图6可以看出，使用5层小波分解与重构变换后的立管压力曲线更加平滑，同时整体趋势和原始数据保持一致。钻井液入口流量分别于20:46和21:50增加，对应的立管压力也相应增加。提取基于滤波后立管压力序列的趋势时，20:48—20:56和21:52—22:04两个时间段内的M_α,t>0.005，G_α,t=1，表明立管压力呈升高趋势。提取基于Δp序列的趋势时，始终满足|M_α,t|≤0.005，G_α,t=0，表明立管压力未发生异常波动。同时，其他时间段内，滤波后立管压力数据和Δp都存在局部的波动，但|M_α,t|≤0.005，G_α,t=0，表明该方法提取的趋势值能够真实反映井下是否发生溢流。

图  6  立管压力序列趋势提取结果

Figure  6.  Extraction results of standpipe pressure sequence trend

下载: 全尺寸图片 幻灯片

2.3   溢流风险指数自适应计算方法

溢流不同时间段内不同特征参数的响应程度不同。溢流初期，出口流量、总池钻井液体积和出口密度基本无变化，而立管压力会呈现逐渐减小的趋势。当溢流流体逐渐接近井口时，立管压力进一步降低，而出口流量迅速增加，总池钻井液体积逐渐增加，钻井液密度降低。因此，基于提取的特征参数序列趋势值，建立了溢流风险指数自适应计算方法。

式中：I_kr,t为溢流风险指数；w_t,fi为t时刻第i个特征参数的权重；M_α,t,fi为t时刻第i个特征参数序列的趋势值；m为当前钻井工况下特征参数的数量；sign为符号标志，当第i个特征参数为总池钻井液体积、出口流量时，sign(f_i)=1，当第i个特征参数为Δp和Δρ时，sign(f_i)=−1；G_a,t,fi为t时刻第i个特征参数序列趋势值对应的等级大小。

溢流风险指数值介于−1到1之间，溢流风险指数越接近1，表示发生溢流的风险越高。当溢流风险指数$\geqslant 0.50$、且持续超过2 min仍满足溢流风险指数$\geqslant 0.50$，则可发出溢流预警信号；反之，则表示无溢流发生。

3.   实例分析

采用塔里木油田某3口井的溢流数据来验证所提出的溢流早期智能检测方法的有效性，每口井的数据采样间隔均为5 s。

井1发生溢流前的录井数据和溢流检测结果如图7所示。13:26钻至3 235.27 m时，总池钻井液体积增加0.5 m³，出口钻井液密度由1.37 kg/L降至1.35 kg/L，现场作业人员发出溢流预警信号。溢流检测结果表明，13:16之后，溢流风险指数$\geqslant 0.50$，可于13:18发出溢流预警信号，比现场作业人员提前8 min预警。

图  7  井1实时钻井数据及溢流风险指数计算结果

Figure  7.  Real-time drilling data and KRI calculation results of Well 1

下载: 全尺寸图片 幻灯片

井2发生溢流前的录井数据和溢流检测结果如图8所示。短起下钻到井底循环过程中，23:37显示总池钻井液体积增大0.4 ${\mathrm{{m}^{3} }}$，立即组织关井。溢流检测方法于23:26显示溢流风险指数$\geqslant 0.50$，可于23:28发出溢流预警信号，比现场作业人员提前9 min预警。

图  8  井2实时钻井数据及溢流风险指数计算结果

Figure  8.  Real-time drilling data and KRI calculation results of Well 2

下载: 全尺寸图片 幻灯片

入口流量接近30 L/s时，出口流量为负值，出口密度恒为0，表明参数测量失效，但并未影响溢流早期检测方法的时效性。出口密度传感器完全失效，测量值随时间保持不变，但在计算溢流风险指数时，其权重较小，溢流风险指数由Δp和总池钻井液体积主导，且溢流初期Δp为关键特征参数，表现为权重最大，随着流体在环空中的运移，总池钻井液体积逐渐成为关键特征参数（见图9）。

图  9  溢流特征参数权重随时间变化的结果

Figure  9.  Variation of weight of kick characteristic parameters with time

下载: 全尺寸图片 幻灯片

图10展示了井3发生溢流前的一段录井数据和溢流检测结果。01:50钻至3243.85 m时出口流量由77.03%急剧升至84.52%，立即组织关井。01:40之后溢流风险指数≥0.50，可于01:42发出溢流预警信号，比现场作业人员提前8 min预警。

图  10  井3实时钻井数据及溢流风险指数计算结果

Figure  10.  Real-time drilling data and KRI calculation results of Well 3

下载: 全尺寸图片 幻灯片

同时，01:07—01:08时间段内溢流风险指数≥0.50，但持续时间仅为1 min，01:08之后溢流风险指数$< 0.50$，故不发出溢流预警信号。该时间段内溢流风险指数≥0.50的主要原因是停泵后钻井液回流使总池钻井液体积在短时间内呈增加趋势。

井1至井3所用的参数值、钻井工况类型、特征参数、现场溢流检测时间、该方法溢流检测时间以及预警提前时间等如表2所示。3口实例井平均预警提前时间为8.3 min，有助于为井控人员赢得更多宝贵时间。

表  2  不同方法检测到的溢流时间对比

Table  2.  Kick time detected by different methods

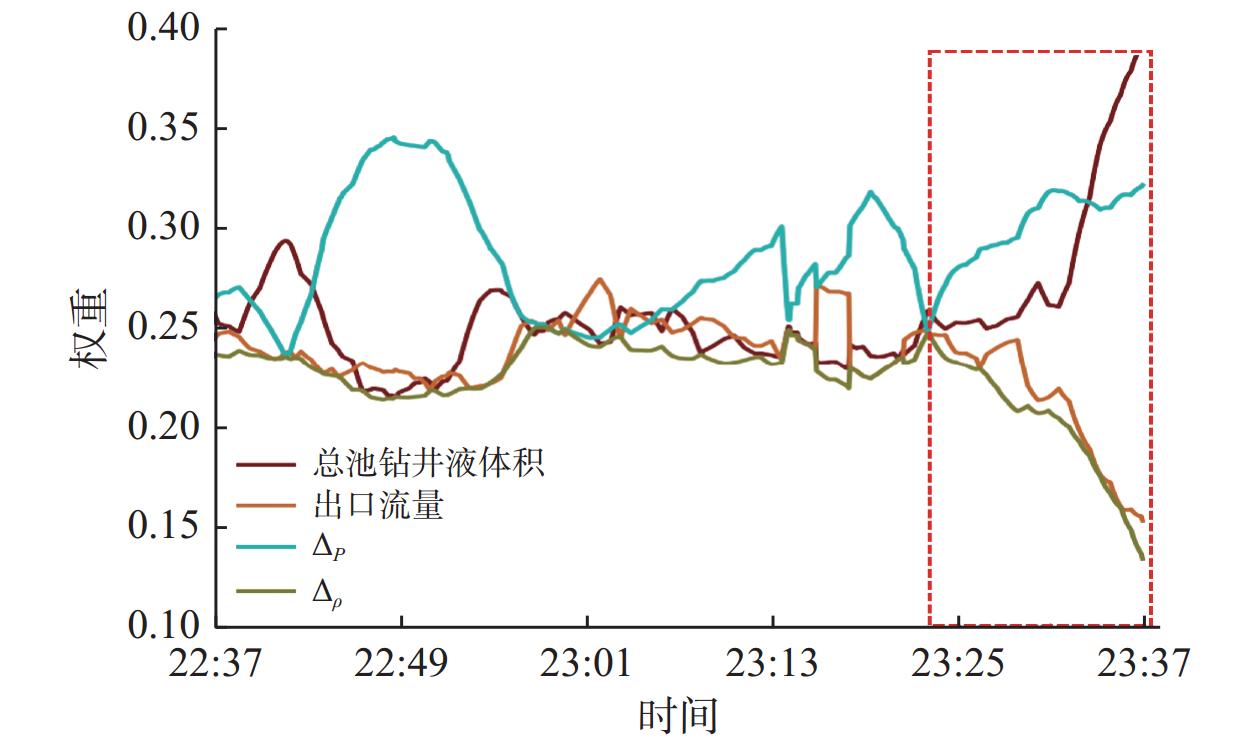
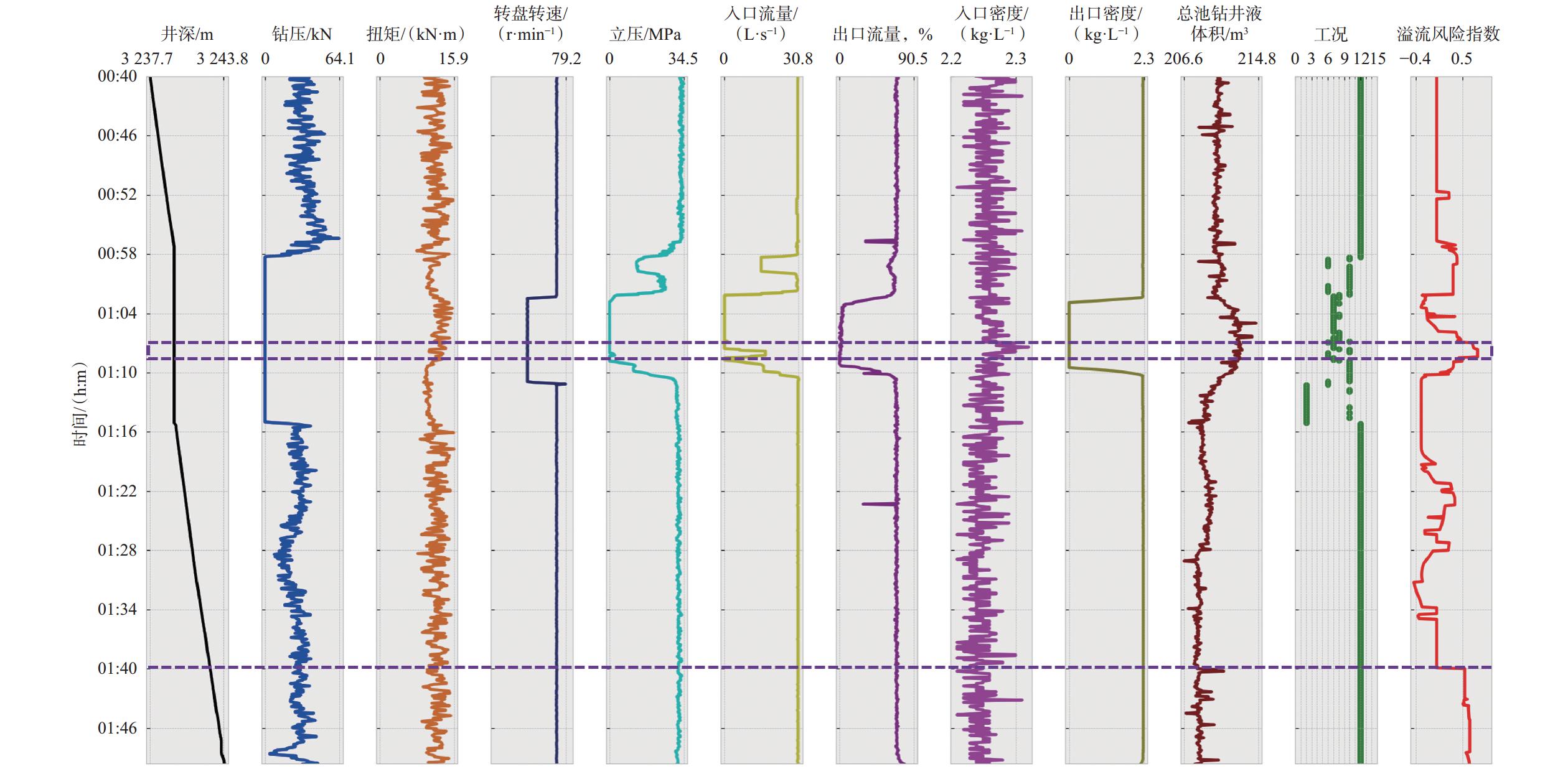
井号	特征参数序列 窗口大小	入口流量序列 趋势阈值	特征参数序列 趋势阈值	工况类型	现场检测到 溢流时间	溢流方法检测 到溢流时间	预警提前时间/min
1	60	0.001	0.001	复合钻进	13:26	13:18	8
2	60	0.001	0.005	原地循环	23:37	23:28	9
3	60	0.001	0.001	复合钻进	01:50	01:42	8

下载: 导出CSV 

| 显示表格

4.   结　论

1）随机森林算法能够有效提取钻井工况与录井参数间的映射关系，工况识别规则与专家经验吻合。

2）钻井工况溢流风险指数自适应计算–溢流检测的方法考虑了溢流数据稀缺、钻井工况对溢流特征参数干扰、溢流不同阶段特征参数响应特性的差异，平均预警时间明显提前。

3）立管压力的准确计算等因素均会影响溢流检测方法的时效性和准确性，需采用更精确的钻井液循环压耗计算模型，同时结合优化算法和统计学等方法实时更新相关参数。此外，提高传感器的测量精度和采样频率，也有助于提高该方法的时效性。