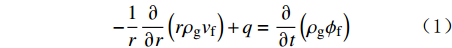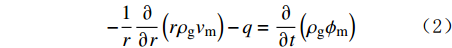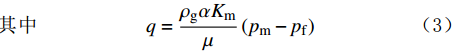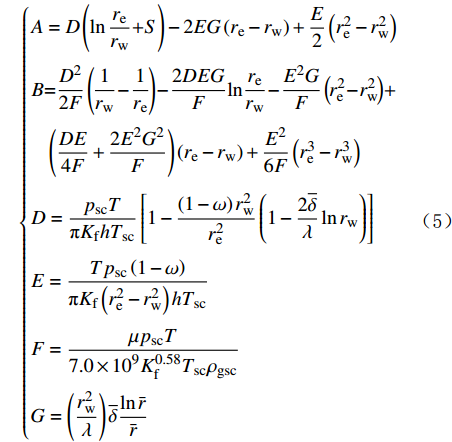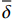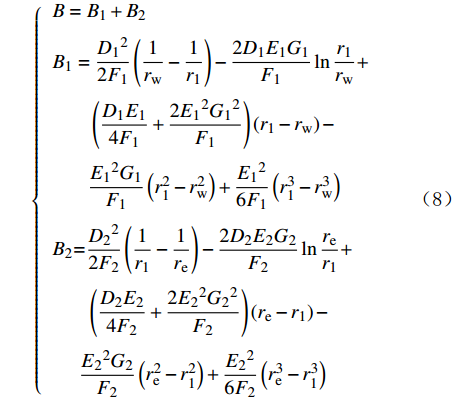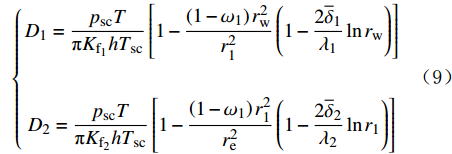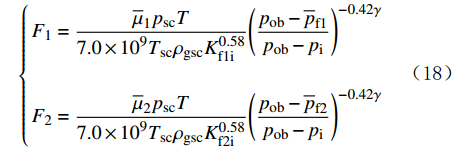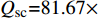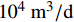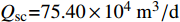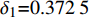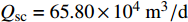考虑应力敏感效应的裂缝性碳酸盐岩气井拟稳态产能预测方法

李江; 陈先超; 高平; 舒成龙

doi:10.11911/syztjs.2021032

考虑应力敏感效应的裂缝性碳酸盐岩气井拟稳态产能预测方法

李江^1,,
陈先超^1, ,,
高平¹,
舒成龙²

1.
成都理工大学能源学院，四川成都 610059
2.
中国石油长庆油田分公司第七采油厂，陕西西安 710000

基金项目: 国家自然科学基金青年科学基金项目“纳米颗粒吸附后强界面效应量化表征及多尺度流固耦合模拟理论研究”（编号：51804048）和油气藏地质及开发工程国家重点实验室开放基金课题“页岩气水平井体积压裂半解析产能预测方法及产能主控因素分析研究”（编号：PLC20180705）联合资助

详细信息

作者简介:
李江（1995—），男，四川泸州人，2019年毕业于成都理工大学石油工程专业，在读硕士研究生，主要从事非常规油气藏工程及数值模拟方面的研究。E-mail：jiang137988@163.com

通讯作者:
陈先超，chenxianchao2005@126.com

中图分类号: TE32⁺8, TE371
计量
- 文章访问数: 768
- HTML全文浏览量: 366
- PDF下载量: 100
出版历程
- 收稿日期: 2020-10-30
- 修回日期: 2021-03-03
- 网络出版日期: 2021-03-10
- 刊出日期: 2021-06-15

A Pseudo-Steady-State Productivity Prediction Method for Fractured Carbonate Gas Wells Considering Stress-Sensitivity Effects

1.
College of Energy, Chengdu University of Technology, Chengdu, Sichuan, 610059, China
2.
No.7 Oil Production Plant, PetroChina Changqing Oilfield Company, Xi’an, Shaanxi, 710000, China

摘要

摘要: 为了准确评价非达西效应和应力敏感效应对裂缝性碳酸盐岩气井产能的影响，建立了一种双重介质径向复合二项式产能综合模型。该模型分为内外2个区域，其中内区用于模拟气井经过压裂后的生产过程，并利用该产能模型计算了四川盆地某裂缝性碳酸盐岩气藏实例井的产能。计算结果表明，与一点法相比，新模型能更合理地预测裂缝性碳酸盐岩储层气井的绝对无阻流量，现场应用效果良好。参数敏感性分析表明，应力敏感因素主要影响气井生产后期；地层系数对气井的绝对无阻流量有较大的影响，地层渗透率和地层厚度越大，越有利于气井开发。综合考虑非达西效应和应力敏感效应的裂缝性碳酸盐岩气藏产能预测模型，为气藏的高效开发和合理配产提供了理论依据。
- 裂缝性储层 /
- 碳酸盐岩 /
- 非达西效应 /
- 应力敏感 /
- 双重介质 /
- 径向复合 /
- 产能预测
Abstract: To accurately evaluate the impact of the non-Darcy and stress-sensitivity effects on the productivity of fractured carbonate gas wells, a new dual-media binomial productivity model for radial compound reservoirs was established. The model is divided into an inner zone and an outer zone, in which the inner zone is designed to simulate the production process of gas wells after fracturing treatment. The new model is used to calculate the productivity of a well in a fractured carbonate gas reservoir in the Sichuan Basin. The calculation results showed that the model can predict the absolute open flow of gas wells in fractured carbonate reservoirs more reasonably and has achieved better field application results than the one-point method. According to the parameter sensitivity analysis, stress sensitivity factors mainly influence the late production stage of gas wells, and the formation coefficient plays an important role in influencing the absolute open flow, which demonstrates that formations with higher permeability and thickness are more favorable to the development of gas wells. The productivity prediction model of fractured carbonate gas reservoirs, which comprehensively considers non-Darcy and stress-sensitive effects, can provide a theoretical basis for the efficient development and reasonable production allocation of gas reservoirs.
- fractured reservoir /
- carbonate rock /
- non-Darcy effect /
- stress sensitivity /
- dual media /
- radial compound /
- productivity forecast

HTML全文

研究表明，非达西效应会显著降低气井的产能，能使气井产能降低20％以上^[1]。应力敏感伤害是裂缝性油气藏主要伤害类型之一，生产压差或采出速度不合适，或能引发应力敏感，造成储层伤害^[2]。压裂直井已广泛应用具有非达西惯性效应的传统二项式产能方程，该方程为现场测试提供了一定的理论基础，例如多点测试、等时测试等^[3-4]。但这些研究主要建立在单一孔隙模型上，并且未考虑应力敏感效应的影响。于是，针对致密砂岩气藏、高压海上气藏及页岩气藏，一些学者提出了考虑应力敏感性的各种产能预测模型^[5-9]，但这些产能预测模型的计算量通常较大，在实践中应用较为复杂。此外，学者们也提出了一些双重孔隙度模型，来预测双重孔隙度储层的压力或产能^[10-15]，但这些模型采用的拉普拉斯、数值反演及大型稀疏矩阵等数值方法过于复杂，也不便于应用^[16]。为此，笔者综合考虑非达西效应和应力敏感效应的影响情况，提出了一种用于裂缝性碳酸盐气井的双重介质二项式产能预测模型，以期为裂缝性碳酸盐岩气藏的产能预测提供理论依据。

1. 双重介质径向复合气井拟稳态产能方程

1.1 物理模型

碳酸盐岩属于裂缝孔隙型储层，因此考虑非达西效应，采用裂缝基质双重介质模型^[17]。双重介质两区径向复合气井的物理模型如图1所示，其基本假设为：1）储层具有双重介质特征，储层全部射开；2）气藏分为内、外两区，内区代表压裂改造区，内区半径为r₁，外区半径为r_e；3）双孔单渗，内外区具有不同的孔渗特征；3）内外区介质间的流动为拟稳定流；4）气井为定产量生产，外边界为定压；5）考虑内区裂缝渗透率变化用于模拟压裂带来的影响。

图 1 双重介质两区径向复合模型

Figure 1. Dual-media model for radial compound reservoirs with two zones

下载: 全尺寸图片幻灯片

1.2 不考虑应力敏感双重介质单区气井拟稳态产能方程

在双重介质模型基础上，不考虑应力敏感，双重介质单区气井平面径向流裂缝和基质连续性方程分别为：

$- \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{\rho _{\rm{g}} }{v_{\rm{f}}}} \right) + q = \frac{\partial }{{\partial t}}\left( {{\rho _{\rm{g}}}{\phi _{\rm{f}}}} \right)$

(1)

$- \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{\rho _{\rm{g}} }{v_{\rm{m}}}} \right) - q = \frac{\partial }{{\partial t}}\left( {{\rho _{\rm{g}}}{\phi _{\rm{m}}}} \right)$

(2)

$\! {\text{其中}} \quad\qquad\;\;\qquad q = \frac{{{\rho _{\rm{g}} }\alpha {K_{\rm{m}}}}}{\mu }\left( {{p_{\rm{m}}} - {p_{\rm{f}}}} \right) \quad\;\;\quad\quad$

(3)

式中：r为径向流半径，m；ρ_g为气体密度，kg/m³；v为气体渗流速度，m/s；q为窜流量，m³/s；ϕ为孔隙度；p为压力，MPa；α为形状因子；μ为气体黏度，mPa·s；K为渗透率，mD；下标f和m分别表示裂缝系统和基质系统。

为便于推导后续方程，定义裂缝系统拟压力 $m\left( {{p_{\rm{f}}}} \right) = 2\int_0^p {\dfrac{p}{{\mu Z}}} {\rm{d}}p$ ，Z为气体压缩系数。

根据以上方程，结合内外边界压力已知条件，代入连续性方程并积分，得到二项式产能表达式：

$m\left( {{p_{{\rm{fe}}}}} \right) - m\left( {{p_{{\rm{fw}}}}} \right){\rm{ = }}A{Q_{{\rm{sc}}}} + BQ_{{\rm{sc}}}^2$

(4)

式中：p_fe为裂缝系统边界压力，MPa；p_fw为裂缝系统井底流压，MPa；Q_sc为气井标况下的产量，10⁴m³/d。

考虑表皮效应，得到各系数的表达式：

$\left\{\!\!\!\! \begin{array}{l} A = D\left( {\ln \dfrac{{{r_{\rm{e}}}}}{{{r_{\rm{w}} }}}{\rm{ + }}S} \right) - 2EG\left( {{r_{\rm{e}}} - {r_{\rm{w}} }} \right) + \dfrac{E}{2}\left( {r_{\rm{e}}^2 - r_{\rm{w}}^2} \right) \\ B\!\!=\!\!\dfrac{{{D^2}}}{{2F}}\left(\! {\dfrac{1}{{{r_{\rm{w}}}}} \!-\! \dfrac{1}{{{r_{\rm{e}} }}}} \! \right) \!-\! \dfrac{{2DEG}}{F} \! \ln \! \dfrac{{{r_{\rm{e}}}}}{{{r_{\rm{w}} }}} \!-\! \dfrac{{{E^2}G}}{F}\left( \! {r_{\rm{e}}^2 \!-\! r_{\rm{w}} ^2} \! \right)\! + \\ \;\;\;\; \left( {\dfrac{{DE}}{{4F}} + \dfrac{{2{E^2}{G^2}}}{F}} \right) \left( {{r_{\rm{e}}} - {r_{\rm{w}} }} \right) + \dfrac{{{E^2}}}{{6F}}\left( {r_{\rm{e}}^3 - r_{\rm{w}}^3} \right) \\ D = \dfrac{{{p_{{\rm{sc}}}}T}}{{{\text{π}} {K_{\rm{f}} }h{T_{{\rm{sc}} }}}}\left[ {1 - \dfrac{{\left( {1 - \omega } \right)r_{\rm{w}} ^2}}{{r_{\rm{e}} ^2}}\left( {1 - \dfrac{{2\overline \delta }}{\lambda }\ln {r_{\rm{w}} }} \right)} \right] \\ E = \dfrac{{T{p_{{\rm{sc}}}}\left( {1 - \omega } \right)}}{{{\text{π}} {K_{\rm{f}}}\left( {r_{\rm{e}}^2 - r_{\rm{w}}^2} \right)h{T_{{\rm{sc}} }}}} \\ F = \dfrac{{\mu {p_{{\rm{sc}} }}T}}{{7.0 \times {{10}^9}K_{\rm{f}} ^{0.58}{T_{{\rm{sc}}}}{\rho _{{\rm{gsc}}}}}} \\ G = \left( {\dfrac{{r_{\rm{w}} ^2}}{\lambda }} \right)\overline \delta \dfrac{{\ln \bar r}}{{\bar r}} \\ \end{array} \right. \!\!\!\!\!\!\!$

(5)

式中：r_w为井眼半径，m；r_e为地层边界半径，m；S为表皮系数；p_sc为标准状态压力，0.101 MPa；ω为弹性储容比；T为地层温度，K；h为地层厚度，m；ρ_gsc为标准状态下的气体密度，kg/m³；T_sc为标准状态温度，293.15 K；λ为窜流系数； $\overline \delta$ 为平均紊流系数； $\bar r$ 为平均泄流半径，m。

则无阻流量计算公式为：

${Q_{\rm{sc}}} = \frac{{ - A + \sqrt {{A^2} + 4B\left[ {m\left( {{p_{{\rm{fe}}}}} \right) - m\left( {{p_{{\rm{sc}}}}} \right)} \right]} }}{{2B}}$

(6)

1.3 不考虑应力敏感双重介质两区径向复合气井拟稳态产能方程

基于双重介质单区气井拟稳态产能公式，运用相同的方法推导得到两区径向复合拟稳态产能公式，其二项式产能表达式和式（4）相同。两区径向复合模型中（见图1），压裂裂缝引起的渗流能力变化等效为内区裂缝渗透率变化，即在考虑压裂裂缝时，通过改变K_f1值来模拟压裂裂缝带来的影响。内、外区的其他条件相同，推导得到各无因次系数：

$\left\{ \begin{array}{l} A = {A_1} + A{}_2 \\ {A_1} = {D_1}\left( {\ln \dfrac{{{r_1}}}{{{r_{\rm{w}} }}} + S} \right) - 2{E_1}{G_1}\left( {{r_1} - {r_{\rm{w}} }} \right) + \dfrac{{{E_1}}}{2}\left( {r_1^2 - r_{\rm{w}} ^2} \right) \\ {A_2} = {D_2}\ln \dfrac{{{r_{\rm{e}}}}}{{{r_1}}} - 2{E_2}{G_2}\left( {{r_{\rm{e}}} - {r_1}} \right) + \dfrac{{{E_2}}}{2}\left( {r_{\rm{e}} ^2 - r_1^2} \right) \\ \end{array} \right.$

(7)

$\left\{ \begin{array}{l} B = {B_1} + {B_2} \\ {B_1} = \dfrac{{{D_1}^2}}{{2{F_1}}}\left( {\dfrac{1}{{{r_{\rm{w}} }}} - \dfrac{1}{{{r_1}}}} \right) - \dfrac{{2{D_1}{E_1}{G_1}}}{{{F_1}}}\ln \dfrac{{{r_1}}}{{{r_{\rm{w}}}}} + \\ \qquad \left( {\dfrac{{{D_1}{E_1}}}{{4{F_1}}} + \dfrac{{2{E_1}^2{G_1}^2}}{{{F_1}}}} \right) \left( {{r_1} - {r_{\rm{w}}}} \right) - \\ \;\;\;\;\;\;\;\; \dfrac{{{E_1}^2{G_1}}}{{{F_1}}}\left( {r_1^2 - r_{\rm{w}} ^2} \right) + \dfrac{{{E_1}^2}}{{6{F_1}}}\left( {r_1^3 - r_{\rm{w}} ^3} \right) \\ {B_2}{\rm{ = }}\dfrac{{{D_2}^2}}{{2{F_2}}}\left( {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_{\rm{e}}}}}} \right) - \dfrac{{2{D_2}{E_2}{G_2}}}{{{F_2}}}\ln \dfrac{{{r_{\rm{e}}}}}{{{r_1}}} + \\ \quad\;\;\;\; \left( {\dfrac{{{D_2}{E_2}}}{{4{F_2}}} + \dfrac{{2{E_2}^2{G_2}^2}}{{{F_2}}}} \right) \left( {{r_{\rm{e}} } - {r_1}} \right)- \\ \;\;\;\;\;\; \dfrac{{{E_2}^2{G_2}}}{{{F_2}}}\left( {r_{\rm{e}}^2 - r_1^2} \right) + \dfrac{{{E_2}^2}}{{6{F_2}}}\left( {r_{\rm{e}}^3 - r_1^3} \right) \\ \end{array} \right.$

(8)

$\left\{ \begin{gathered} {D_1} = \frac{{{p_{\rm{sc}}}T}}{{{\text{π}} {K_{{{\rm{f}} _1}}}h{T_{\rm{sc}}}}}\left[ {1 - \frac{{\left( {1 - {\omega _1}} \right)r_{\rm{w}}^2}}{{r_1^2}}\left( {1 - \frac{{2{\overline{\delta} _1} }}{{{\lambda _1}}}\ln {r_{\rm{w}}}} \right)} \right] \\ {D_2} = \frac{{{p_{\rm{sc}}}T}}{{{\text{π}} {K_{{{\rm{f}} _2}}}h{T_{{\rm{sc}}}}}}\left[ {1 - \frac{{\left( {1 - {\omega _1}} \right)r_1^2}}{{r_{\rm{e}} ^2}}\left( {1 - \frac{{2{\overline{\delta} _2} }}{{{\lambda _2}}}\ln {r_1}} \right)} \right] \\ \end{gathered} \right.$

(9)

$\left\{ \begin{gathered} {\overline{\delta} _1} {\rm{ = }}\frac{1}{{1 + \dfrac{{3.5 \times {{10}^9}{\rho _{\rm{gsc}}}{Q_{\rm{sc}}}}}{{{{\overline \mu }_1}{\text{π}} h{K_{{\rm{f}} 1}}^{0.42}}}\dfrac{1}{{{{\bar r}_1}}}}} \\ {\overline{\delta} _2} {\rm{ = }}\frac{1}{{1 + \dfrac{{3.5 \times {{10}^9}{\rho _{\rm{gsc}}}{Q_{\rm{sc}}}}}{{{\overline{\mu} _2} {\text{π}} h{K_{{\rm{f}} 2}}^{0.42}}}\dfrac{1}{{{{\bar r}_2}}}}} \\ \end{gathered} \right.$

(10)

${\left\{ \begin{array}{l} {E_1} = \dfrac{{T{p_{{\rm{sc}}}}\left( {1 - {\omega _1}} \right)}}{{{\text{π}} {K_{{\rm{f}}1}}\left( {r_1^2 - r_{\rm{w}}^2} \right)h{T_{\rm{sc}}}}}\\ {E_2} = \dfrac{{T{p_{\rm{sc}}}\left( {1 - {\omega _2}} \right)}}{{{\text{π}} {K_{{\rm{f}}2}}\left( {r_{\rm{e}}^2 - r_1^2} \right)h{T_{\rm{sc}}}}} \end{array} \right.}$

(11)

${\left\{ \begin{array}{l} {\omega _1}{\rm{ = }}\dfrac{{{{\left( {\phi {C_{\rm{t}}}} \right)}_{{\rm{f1}}}}}}{{{{\left( {\phi {C_{\rm{t}}}} \right)}_{{\rm{f1}}}}{\rm{ + }}{{\left( {\phi {C_{\rm{t}}}} \right)}_{{\rm{m1}}}}}}\\ {\omega _{\rm{2}}}{\rm{ = }}\dfrac{{{{\left( {\phi {C_{\rm{t}}}} \right)}_{{\rm{f2}}}}}}{{{{\left( {\phi {C_{\rm{t}}}} \right)}_{{\rm{f2}}}}{\rm{ + }}{{\left( {\phi {C_{\rm{t}}}} \right)}_{{\rm{m2}}}}}} \end{array} \right.}$

(12)

$\left\{ \begin{gathered} {F_1} = \dfrac{{{\overline{\mu} _1} {p_{\rm{sc}}}T}}{{7.0 \times {{10}^9}K_{{\rm{f}} 1}^{0.58}{T_{\rm{sc}}}{\rho _{\rm{gsc}}}}} \\ {F_2} = \dfrac{{{\overline{\mu} _2} {p_{\rm{sc}}}T}}{{7.0 \times {{10}^9}K_{{\rm{f}} 2}^{0.58}{T_{\rm{sc}}}{\rho _{\rm{gsc}}}}} \\ \end{gathered} \right.$

(13)

$\left\{ \begin{array}{l} {G_1} = \left( {\dfrac{{r_{\rm{w}}^2}}{{{\lambda _1}}}} \right){\overline{\delta} _1} \dfrac{{\ln {{\bar r}_1}}}{{{{\bar r}_1}}}\\ {G_2} = \left( {\dfrac{{r_1^2}}{{{\lambda _2}}}} \right){\overline{\delta} _2} \dfrac{{\ln {{\bar r}_2}}}{{{{\bar r}_2}}} \end{array} \right.$

(14)

$\left\{ \begin{array}{l} {\lambda _1}{\rm{ = }}\alpha r_{\rm{w}}^2\dfrac{{{K_{\rm{m}}}_{{\rm{1i}}}}}{{{K_{{\rm{f1i}}}}}}\\ {\lambda _2}{\rm{ = }}\alpha r_{\rm{w}}^2\dfrac{{{K_{{\rm{m2i}}}}}}{{{K_{\rm{f2i}}}}} \end{array} \right.$

(15)

式中：C_t为岩石压缩系数，MPa^–1；下标1和2分别表示内区和外区；下标i表示初始状态。

1.4 考虑应力敏感双重介质两区径向复合气井拟稳态产能方程

致密碳酸盐岩储层属于裂缝孔隙型储层，除了考虑非达西效应和应力敏感效应之外，应该采用裂缝、基质双重介质复合模型来计算其产能。因此，基于双孔单渗模型，建立了考虑应力敏感双重介质两区径向复合气井拟稳态产能公式。在不考虑应力敏感模型基础之上，根据文献[18]得到裂缝性碳酸盐岩储层应力敏感关系式：

${K_{\rm{f}} } = {K_{\rm{fi}}}{\left( {\frac{{{p_{\rm{ob}}} - {p_{\rm{f}} }}}{{{p_{\rm{ob}}} - {p_{\rm{fi}}}}}} \right)^{ - \gamma }}$

(16)

修正拟压力关系式：

${m^*}\left( {{p_{\rm{f}}}} \right) = 2\int_0^p {\frac{p}{{\mu Z}}} {\left( {\frac{{{p_{\rm{ob}}} - p}}{{{p_{\rm{ob}}} - {p_{\rm{i}}}}}} \right)^{ - \gamma }}{\rm{d}}p$

(17)

式中：p_ob为上覆岩层压力，MPa；γ为裂缝应力敏感系数。

对于致密碳酸盐岩地层，窜流系数很小，可以忽略不计。推导过程如前所述，得到两区径向复合拟稳态二项式产能表达式，式中各系数如式（7）—式（15）所示，其中式（13）变为：

$\left\{ \begin{gathered} {F_1} = \frac{{{\overline{\mu} _1} {p_{\rm{sc}}}T}}{{7.0 \times {{10}^9}{T_{{\rm{sc}} }}{\rho _{\rm{gsc}}}K_{{\rm{f1i}}}^{0.58}}}{\left( {\frac{{{p_{\rm{ob}}} - {\overline{p}_{\rm{f1}}}} }{{{p_{\rm{ob}}} - {p_{\rm{i}}}}}} \right)^{ - 0.42\gamma }} \\ {F_2} = \frac{{{\overline {\mu} _2} {p_{{\rm{sc}} }}T}}{{7.0 \times {{10}^9}{T_{{\rm{sc}} }}{\rho _{\operatorname{gsc} }}K_{{\rm{f2i}}}^{0.58}}}{\left( {\frac{{{p_{\operatorname{ob} }} - {\overline{p}_{{\rm{f}} 2}} }}{{{p_{{\rm{ob}}}} - {p_{\rm{i}}}}}} \right)^{ - 0.42\gamma }} \\ \end{gathered} \right.$

(18)

2. 实例验证

以四川盆地某区块裂缝性碳酸盐岩气藏为例，计算该区块压裂直井A1井的产能。根据双重介质两区试井模型^[19]分析得：内区半径r₁为99.55 m，内区裂缝渗透率K_f1i为2.08 mD，内区弹性储容比为0.45，内区窜流系数为5.6×10^–3；外区半径r_e为690.34 m，外区裂缝渗透率K_f2i为1.89 mD，外区弹性储容比为0.13，外区窜流系数为2.0×10^–10，双重介质形状因子α为0.6。其他主要参数为：储层中部垂深5 297.30 m；初始地层压力p_i为58.04 MPa；储层平均孔隙度ϕ为3.8%，岩石压缩系数C_t为0.002 MPa^–1，标准状态温度T_sc为293.15 K，标准状态压力p_sc为0.101 MPa，井底温度为152.62 ℃，井口温度为40.3 ℃，储层有效厚度28.10 m，井眼半径r_w为0.044 m，表皮系数S为0.032 2；参考邻井气体组分分析结果，计算临界参数，并利用不同产能模型计算该井的产能。

首先，利用不考虑应力敏感的单区双重介质模型，计算裂缝平均渗透率、平均储容比、平均传导系数、平均压力、平均黏度、平均半径和平均紊流系数，代入式（5）得到A=95.752 6、B=19.406 6，代入式（6）得到 ${Q_{\rm{sc}}}{\rm{ = }}81.67 \times$ ${10^4}\;{\rm{{m^3}}/d}$ 。

然后，利用不考虑压力敏感的双重介质两区径向复合模型，计算平均压力、内区半径、外区半径、内区紊流系数和外区紊流系数，代入式（7）—式（15），得到的系数见表1，将计算参数代入式（6）得到 ${Q_{\rm{sc}}}{\rm{ = }}75.40 \times {10^4}\;{\rm{{m^3}}/d}$ 。

表 1 不同产能模型的气井参数计算结果

Table 1. Calculation results of gas well parameters from different productivity models

参数	计算结果		参数	计算结果
参数	模型1	模型2	参数	模型1	模型2
A	73.814 4	72.864 9	B	23.163 9	24.973 8
A₁	59.499 0	58.700 6	A₂	14.315 4	14.164 4
B₁	18.050 5	19.919 8	B₂	5.113 4	5.054 0
D₁	7.407 5	7.308 0	D₂	634.887 5	620.830 5
E₁	4.126×10^–4	4.071×10^–4	E₂	1.488×10^–5	1.468×10^–5
F₁	34.533 9	30.458 9	F₂	87.535 9	84.677 6
G₁	1.0827×10^–2	1.0107×10^–2	G₂	6.9299×10⁴	6.8679×10⁴
注：模型1为不考虑应力敏感的单区双重介质模型，模型2为考虑应力敏感双重介质两区径向复合模型。

下载: 导出CSV

| 显示表格

最后，用考虑应力敏感双重介质两区径向复合模型，利用径向压力公式计算内区边界压力，然后求算术平均压力，取内区紊流系数 ${\delta _1}{\rm{ = }}0.372\;5$ ，外区紊流系数 ${\delta _2}{\rm{ = }}0.915\;6$ ，代入式（8）—式（12）、式（14）—式（15）和式（18），得到的系数见表1，将计算参数代入式（6）得到 ${Q_{{\rm{sc}}}} = 65.80 \times {10^4}\;{\rm{{m^3}}/d}$ 。

不同产能模型计算结果见表2。从表2可以看出，考虑应力敏感双重介质两区径向复合模型的计算结果与稳定产能试井解释结果（63.83×10⁴ m³/d）最为接近，因此考虑应力敏感的产能模型能更合理地预测裂缝性碳酸盐岩储层气井的无阻流量。

表 2 不同产能模型计算结果对比

Table 2. Comparisons among calculation results from different productivity models

产能模型	无阻流量/ （10⁴m³·d^–1）	与试井解释结果的相对误差，%
一点法	54.47	–13.54
不考虑应力敏感的单区径向复合模型	81.67	29.63
不考虑应力敏感的两区径向复合模型	75.40	19.68
考虑应力敏感的两区径向复合模型	65.80	4.44

下载: 导出CSV

| 显示表格

3. 参数敏感性分析

采用控制变量法，变化单一参数，利用考虑应力敏感双重介质两区径向复合气井拟稳态产能方程（计算参数见“实例验证”部分）分析应力敏感系数、上覆岩层压力、初始地层压力及地层系数对生产动态的影响。

3.1 应力敏感系数

其他参数不变，裂缝应力敏感系数γ分别为0，0.2，0.4，0.6和0.8时，气井流入动态曲线如图2所示。从图2可以看出，随着井底流压降低，应力敏感效应越来越明显，应力敏感系数越大，产量降低越明显。实际开发过程中，由于持续开采，将导致储层岩石物性随着应力变化而发生变化，因此需要考虑应力敏感的影响。

图 2 不同应力敏感系数下的IPR曲线

Figure 2. Inflow performance relation (IRP) curves under different stress sensitivity coefficients

下载: 全尺寸图片幻灯片

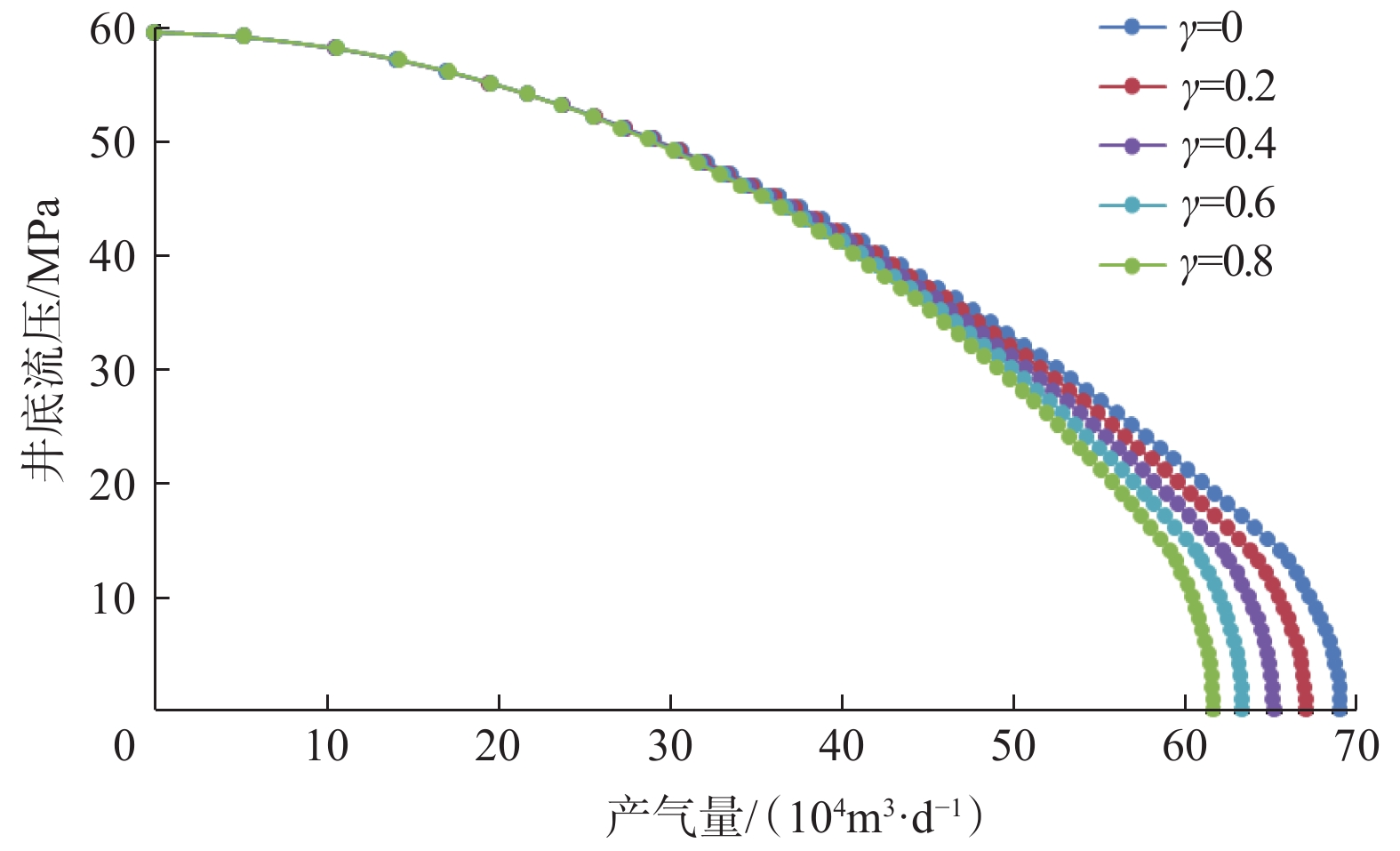
3.2 上覆岩层压力

其他参数不变，上覆岩层压力p_ob分别为100，110，120，130和140 MPa时，气井流入动态曲线如图3所示。从图3可以看出，随着井底流压降低，上覆岩层压力作用效果越来越明显；上覆岩层压力越小，产量降低越明显。这是因为较低的上覆岩层压力将导致地层能量不足，使产能降低。

图 3 不同上覆岩层压力下的IPR曲线

Figure 3. IPR curves under different overburden pressures

下载: 全尺寸图片幻灯片

3.3 初始地层压力

其他参数不变，初始地层压力p_i分别为58.50，59.00，59.42，60.00和60.50 MPa时，气井流入动态曲线如图4所示。从图4可以看出，初始地层压力增大，地层能量增大，该作用要比应力敏感作用大；随着初始地层压力增大，气井产量逐渐增大。从流入动态曲线可以看出，随着井底流压降低，初始地层压力降低，产量明显降低；但整体来看，初始地层压力的影响较小。

图 4 不同初始地层压力下的IPR曲线

Figure 4. IPR curves under different initial formation pressures

下载: 全尺寸图片幻灯片

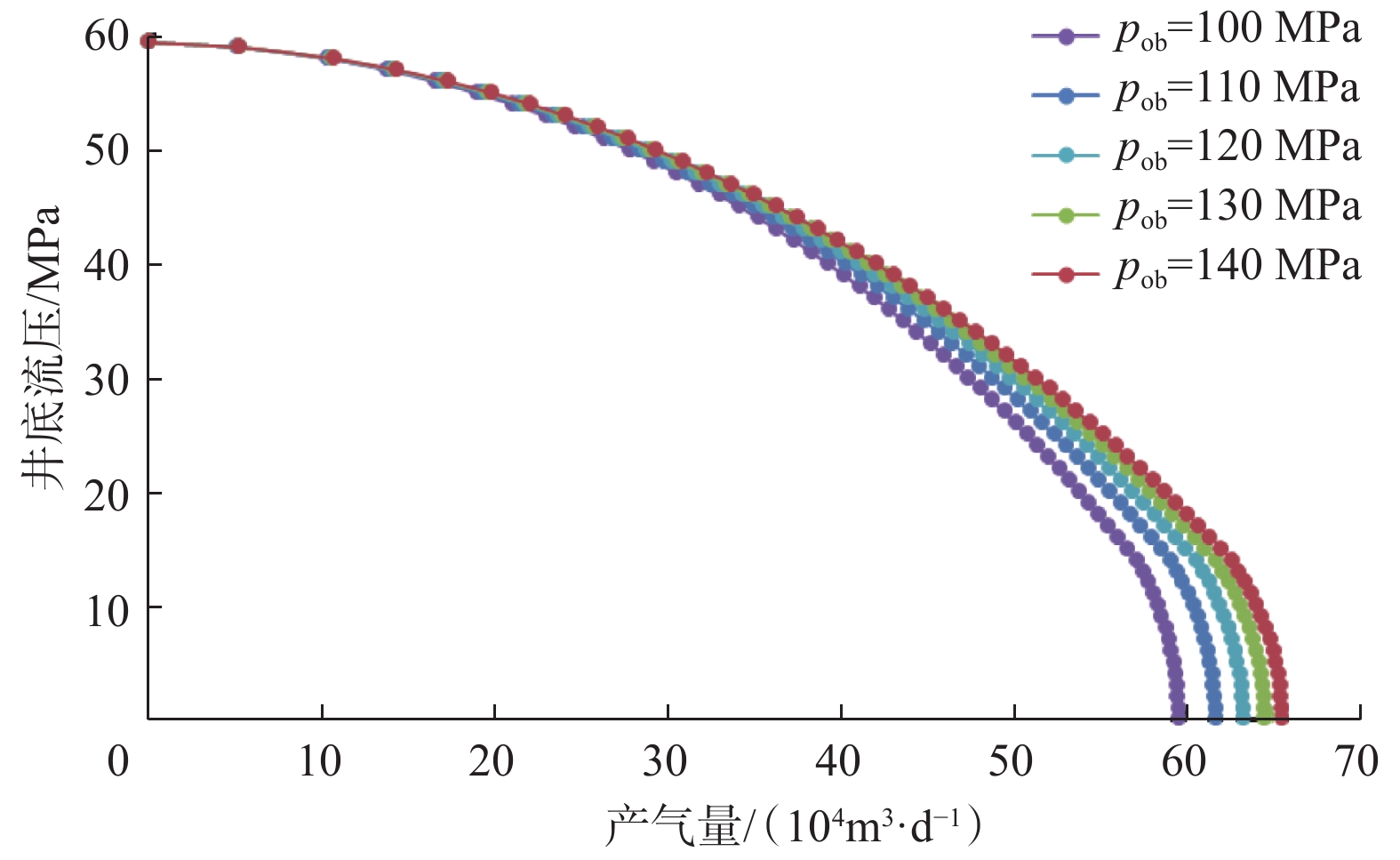
3.4 地层系数

其他参数不变，地层系数Kh分别为50.00，55.00，58.07，65.00和70.00 mD·m时，气井流入动态曲线如图5所示。从图5可以看出，地层系数对产能影响较为明显，随着地层系数增大，气井产量逐渐增大。从流入动态曲线可以看出，随着井底流压降低，地层系数的作用越来越明显；地层系数越小，产量降低越明显。

图 5 不同地层系数下的IPR曲线

Figure 5. IPR curves under different formation coefficients

下载: 全尺寸图片幻灯片

4. 结　论

1）基于双重介质模型，建立了综合考虑非达西效应和应力敏感效应的裂缝性碳酸盐岩气藏产能二项式方程。

2）实例计算和试井解释的气井无阻流量对比表明，综合考虑非达西和应力敏感效应的双重介质两区径向复合模型比一点法的预测准确性更高。

3）应力敏感性效应对气井产能的影响主要体现在生产阶段后期，产能随应力敏感系数增大而降低；地层系数对气井产能的影响体现在整个生产阶段，产能随地层系数增大而升高。

图 1 双重介质两区径向复合模型

Figure 1. Dual-media model for radial compound reservoirs with two zones

下载: 全尺寸图片幻灯片

图 2 不同应力敏感系数下的IPR曲线

Figure 2. Inflow performance relation (IRP) curves under different stress sensitivity coefficients

下载: 全尺寸图片幻灯片

图 3 不同上覆岩层压力下的IPR曲线

Figure 3. IPR curves under different overburden pressures

下载: 全尺寸图片幻灯片

图 4 不同初始地层压力下的IPR曲线

Figure 4. IPR curves under different initial formation pressures

下载: 全尺寸图片幻灯片

图 5 不同地层系数下的IPR曲线

Figure 5. IPR curves under different formation coefficients

下载: 全尺寸图片幻灯片

表 1 不同产能模型的气井参数计算结果

Table 1 Calculation results of gas well parameters from different productivity models

参数	计算结果		参数	计算结果
参数	模型1	模型2	参数	模型1	模型2
A	73.814 4	72.864 9	B	23.163 9	24.973 8
A₁	59.499 0	58.700 6	A₂	14.315 4	14.164 4
B₁	18.050 5	19.919 8	B₂	5.113 4	5.054 0
D₁	7.407 5	7.308 0	D₂	634.887 5	620.830 5
E₁	4.126×10^–4	4.071×10^–4	E₂	1.488×10^–5	1.468×10^–5
F₁	34.533 9	30.458 9	F₂	87.535 9	84.677 6
G₁	1.0827×10^–2	1.0107×10^–2	G₂	6.9299×10⁴	6.8679×10⁴
注：模型1为不考虑应力敏感的单区双重介质模型，模型2为考虑应力敏感双重介质两区径向复合模型。

下载: 导出CSV

表 2 不同产能模型计算结果对比

Table 2 Comparisons among calculation results from different productivity models

产能模型	无阻流量/ （10⁴m³·d^–1）	与试井解释结果的相对误差，%
一点法	54.47	–13.54
不考虑应力敏感的单区径向复合模型	81.67	29.63
不考虑应力敏感的两区径向复合模型	75.40	19.68
考虑应力敏感的两区径向复合模型	65.80	4.44

下载: 导出CSV

参考文献(19)

[1]	SMITH M B, BALE A, BRITT L K, et al. An investigation of non-Darcy flow effects on hydraulic fractured oil and gas well performance[R]. SPE 90864, 2004.
[2]	张鹏,吴通,李中,等. BP神经网络法预测顺北超深碳酸盐岩储层应力敏感程度[J]. 石油钻采工艺,2020,42(5):622–626. ZHANG Peng, WU Tong, LI Zhong, et al. Application of BP neural network method to predict the stress sensitivity of ultra deep carbonate reservoir in Shunbei Oilfield[J]. Oil Drilling & Production Technology, 2020, 42(5): 622–626.
[3]	ZHANG Qi, SU Yuliang, WANG Wendong, et al. A new semi-analytical model for simulating the effectively stimulated volume of fractured wells in tight reservoirs[J]. Journal of Natural Gas Science and Engineering, 2015, 27(3): 1834–1845.
[4]	陈军,刘太雷,任洪明. 考虑非达西流动影响的底水气藏产能新方法[J]. 特种油气藏,2019,26(2):91–95. CHEN Jun, LIU Tailei, REN Hongming. A new bottom-aquifer reservoir productivity equation based on non-darcy flow[J]. Special Oil & Gas Reservoirs , 2019, 26(2): 91–95.
[5]	杨滨,姜汉桥,陈民锋,等. 应力敏感气藏产能方程研究[J]. 西南石油大学学报(自然科学版),2008,30(5):158–160. YANG Bin, JIANG Hanqiao, CHEN Minfeng, et al. Deliverability equation for stress-sensitive gas reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2008, 30(5): 158–160.
[6]	温伟明,朱绍鹏,李茂. 海上异常高压气藏应力敏感特征及产能方程:以莺歌海盆地为例[J]. 天然气工业,2014,34(9):59–63. WEN Weiming, ZHU Shaopeng, LI Mao. Stress sensitivity features and productivity equations of offshore abnormal high-pressure gas reservoirs: a case study from the Yinggehai Basin[J]. Natural Gas Industry, 2014, 34(9): 59–63.
[7]	邓佳,朱维耀,刘锦霞,等. 考虑应力敏感性的页岩气产能预测模型[J]. 天然气地球科学,2013,24(3):456–460, 638. DENG Jia, ZHU Weiyao, LIU Jingxia, et al. Productivity prediction model of shale gas considering stress sensitivity[J]. Natural Gas Geoscience, 2013, 24(3): 456–460, 638.
[8]	JIANG Liwu, LIU Tongjing, YANG Daoyong. Effect of stress-sensitive fracture conductivity on transient pressure behavior for a horizontal well with multistage fractures[J]. SPE Journal, 2019, 24(3): 1342–1363. doi: 10.2118/194509-PA
[9]	HUANG Shijun, DING Guangyang, WU Yonghui, et al. A semi-analytical model to evaluate productivity of shale gas wells with complex fracture networks[J]. Journal of Natural Gas Science & Engineering, 2018, 50: 374–383.
[10]	黄天坤,王德龙,王丽影,等. 双重介质页岩气藏水平井压力动态特征[J]. 成都理工大学学报(自然科学版),2019,46(2):212–220. HUANG Tiankun, WANG Delong, WANG Liying, et al. Study on the pressure dynamic feature of horizontal wells in dual-porosity shale gas reservoir[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2019, 46(2): 212–220.
[11]	姜瑞忠,原建伟,崔永正,等. 考虑岩石变形的页岩气藏双重介质数值模拟[J]. 油气地质与采收率,2019,26(4):70–76. JIANG Ruizhong, YUAN Jianwei, CUI Yongzheng, et al. Dual media numerical simulation of shale gas reservoirs considering rock deformation[J]. Petroleum Geology and Recovery Efficiency, 2019, 26(4): 70–76.
[12]	赵海洋,贾永禄,蔡明金,等. 低渗透双重介质垂直裂缝井产能分析[J]. 西南石油大学学报(自然科学版),2009,31(2):71–73. ZHAO Haiyang, JIA Yonglu, CAI Mingjin, et al. Deliverability analysis of vertical fracture wells in low permeability dual porosity reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2009, 31(2): 71–73.
[13]	蔡建超,郭士礼,游利军,等. 裂缝–孔隙型双重介质油藏渗吸机理的分形分析[J]. 物理学报,2013,62(1):220–224. CAI Jianchao, GUO Shili, YOU Lijun, et al. Fractal analysis of spontaneous imbibition mechanism in fractured-porous dual media reservoir[J]. Acta Physica Sinica, 2013, 62(1): 220–224.
[14]	XUE Yi, TENG Teng, DANG Faning, et al. Productivity analysis of fractured wells in reservoir of hydrogen and carbon based on dual-porosity medium model[J]. International Journal of Hydrogen Energy, 2020, 45(39): 20240–20249. doi: 10.1016/j.ijhydene.2019.11.146
[15]	王建忠,姚军,张凯,等. 变渗透率模量与双重孔隙介质的压力敏感性[J]. 中国石油大学学报(自然科学版),2010,34(3):80–83, 88. WANG Jianzhong, YAO Jun, ZHANG Kai, et al. Variable permeability modulus and pressure sensitivity of dual-porosity medium[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010, 34(3): 80–83, 88.
[16]	WANG Wendong, FAN Dian, SHENG Guanglong, et al. A review of analytical and semi-analytical fluid flow models for ultra-tight hydrocarbon reservoirs[J]. Fuel, 2019, 256: 115737. doi: 10.1016/j.fuel.2019.115737
[17]	WARREN J E, ROOT P J. The behavior of naturally fractured reservoirs[J]. Society of Petroleum Engineers Journal, 1963, 3(3): 245–255. doi: 10.2118/426-PA
[18]	高树生,刘华勋,任东,等. 缝洞型碳酸盐岩储层产能方程及其影响因素分析[J]. 天然气工业,2015,35(9):48–54. GAO Shusheng, LIU Huaxun, REN Dong, et al. Deliverability equation of fracture-cave carbonate reservoirs and its influential factors[J]. Natural Gas Industry, 2015, 35(9): 48–54.
[19]	姜瑞忠,高岳,孙召勃,等. 双重介质低渗油藏偏心压裂直井井底压力特征[J]. 断块油气田,2020,27(6):778–783. JIANG Ruizhong, GAO Yue, SUN Zhaobo, et al. Bottom pressure characteristics for eccentric fracture vertical well in dual-medium low-permeability reservoir[J]. Fault-Block Oil & Gas Field, 2020, 27(6): 778–783.

施引文献(20)

期刊类型引用(17)

1.	蔡珺君，彭先，李隆新，刘微，甘笑非，邓庄，李玥洋，王蓓，胡怡. “一点法”产能评价方法的内涵、矿场应用及改进. 断块油气田. 2024(01): 123-133 . 百度学术
2.	李冬梅，李会会，朱苏阳. 大尺度离散裂缝的渗透率应力敏感研究——以顺北油田为例. 断块油气田. 2024(01): 147-153 . 百度学术
3.	郑函庆，刘军严，丁心鲁，汪坤，封猛，冯光. 富满地区断控缝洞型油藏试油初期产能预测方法. 油气井测试. 2024(01): 72-78 . 百度学术
4.	傅超，杨进，刘华清，殷启帅，王磊，胡志强. 多维度深水浅层建井方式优选方法研究. 石油钻探技术. 2024(03): 40-46 . 本站查看
5.	丁心鲁，黎丽丽，郑函庆，刘勇，封猛，刘爽. 超深层白云岩储层油气产能试油前预测方法. 石油钻采工艺. 2024(01): 67-77 . 百度学术
6.	张杜杰. 超深致密砂岩气藏应力敏感性实验研究. 复杂油气藏. 2024(02): 217-224 . 百度学术
7.	王璐，罗瑞兰，张林，俞霁晨，邹瑞，邹润，张一帆. 超深层碳酸盐岩气藏产能预测模型及影响因素研究. 油气地质与采收率. 2024(03): 88-98 . 百度学术
8.	原建伟，刘美佳，李超，吴春新，马栋. 窄河道油藏水平井边界校正系数研究. 石油钻探技术. 2023(01): 86-90 . 本站查看
9.	郭为，柳家正，张晓伟，滕柏路，康莉霞，高金亮，刘钰洋，罗万静. 考虑蠕变效应的页岩气水平井控压生产增产机理研究. 力学学报. 2023(03): 630-642 . 百度学术
10.	蔡珺君，李小刚，朱文涛，彭先，李隆新，刘微，王蓓，马旸. 整合测井资料的碳酸盐岩气田“一点法”产能评价方法. 断块油气田. 2023(02): 301-307 . 百度学术
11.	孙鑫，刘礼军，侯树刚，戴彩丽，杜焕福，王春伟. 基于页岩油水两相渗流特性的油井产能模拟研究. 石油钻探技术. 2023(05): 167-172 . 本站查看
12.	付德奎. 普光气田超深高含硫水平井开发测井先导性试验. 断块油气田. 2023(06): 1007-1012 . 百度学术
13.	袁飞宇，唐潮，张超，付亚飞，陈波. 团簇效应对裂缝连通性的影响. 特种油气藏. 2023(06): 107-113 . 百度学术
14.	俞天喜，王雷，陈蓓蓓，孙锡泽，李圣祥，朱振龙. 基于盐溶和蠕变作用的含盐储层裂缝导流能力变化规律研究与应用. 特种油气藏. 2023(06): 157-164 . 百度学术
15.	李虹，于海洋，杨海烽，邓彤，李旭，吴阳. 裂缝性非均质致密储层自适应应力敏感性研究. 石油钻探技术. 2022(03): 99-105 . 本站查看
16.	张金发，李亭，吴警宇，管英柱，徐摩，但植华，周明秀. 特低渗透砂岩储层敏感性评价与酸化增产液研制. 特种油气藏. 2022(05): 166-174 . 百度学术
17.	刘慧，丁心鲁，张士杰，方云贵，郝晓波，郑玮鸽. 地下储气库注气过程一体化压力及地层参数计算方法. 石油钻探技术. 2022(06): 64-71 . 本站查看

其他类型引用(3)

资源附件(0)

图(5) / 表(2)

计量

文章访问数: 768
HTML全文浏览量: 366
PDF下载量: 100
被引次数: 20

1. 双重介质径向复合气井拟稳态产能方程
1.1 物理模型
1.2 不考虑应力敏感双重介质单区气井拟稳态产能方程
1.3 不考虑应力敏感双重介质两区径向复合气井拟稳态产能方程
1.4 考虑应力敏感双重介质两区径向复合气井拟稳态产能方程
2. 实例验证
3. 参数敏感性分析
3.1 应力敏感系数
3.2 上覆岩层压力
3.3 初始地层压力
3.4 地层系数
4. 结　论

1. 双重介质径向复合气井拟稳态产能方程
1.1 物理模型
1.2 不考虑应力敏感双重介质单区气井拟稳态产能方程
1.3 不考虑应力敏感双重介质两区径向复合气井拟稳态产能方程
1.4 考虑应力敏感双重介质两区径向复合气井拟稳态产能方程
2. 实例验证
3. 参数敏感性分析
3.1 应力敏感系数
3.2 上覆岩层压力
3.3 初始地层压力
3.4 地层系数
4. 结　论

参考文献(19)

施引文献(20)

资源附件(0)

考虑应力敏感效应的裂缝性碳酸盐岩气井拟稳态产能预测方法

作者简介: 李江（1995—），男，四川泸州人，2019年毕业于成都理工大学石油工程专业，在读硕士研究生，主要从事非常规油气藏工程及数值模拟方面的研究。E-mail：jiang137988@163.com

通讯作者: 陈先超，chenxianchao2005@126.com

计量

出版历程