深水钻井浅水流地层井眼坍塌影响因素分析

孙金; 吴时国; 邓金根; 王吉亮

doi:10.11911/syztjs.2019032

深水钻井浅水流地层井眼坍塌影响因素分析

孙金^1,,
吴时国^{1, 2},
邓金根³,
王吉亮¹

1.
中国科学院深海科学与工程研究所，海南三亚 572000
2.
青岛海洋科学与技术国家实验室海洋地质过程与环境功能实验室，山东青岛 266061
3.
中国石油大学（北京）石油工程学院，北京 102249

基金项目: 国家重点基础研究发展计划（“973”计划）项目“深水钻井浅层地质灾害形成机理及预测方法”（编号：2015CB251201）、青岛海洋科学与技术国家实验室海洋地质过程与环境功能实验室开放基金资助项目“深水钻井浅层超压地质灾害评价及防治技术”（编号：MGQNLM-KF201717）、海南省自然科学基金创新研究团队项目“南海深水天然气水合物试采关键技术研究”（编号：2018CXTD346）联合资助

详细信息

作者简介:
孙金（1987—），男，山东枣庄人，2009年毕业于中国石油大学（华东）石油工程专业，2016年获中国石油大学（北京）油气井工程专业博士学位，助理研究员，主要从事深水钻井、深水地质灾害方面的研究工作。E-mail: sunjin@idsse.ac.cn

中图分类号: TE21
计量
- 文章访问数: 3601
- HTML全文浏览量: 2120
- PDF下载量: 57
出版历程
- 收稿日期: 2018-11-26
- 修回日期: 2019-02-18
- 网络出版日期: 2019-03-14
- 刊出日期: 2019-02-28

Analysis of the Contributing Factors to Wellbore Collapse in Shallow Water Flow Formations for Deepwater Drilling

1.
Institute of Deep-Sea Science and Engineering, Chinese Academy of Sciences, Sanya, Hainan, 572000, China
2.
Laboratory for Marine Geology, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong, 266061, China
3.
College of Petroleum Engineering, China University of Petroleum(Beijing), Beijing, 102249, China

摘要

摘要:
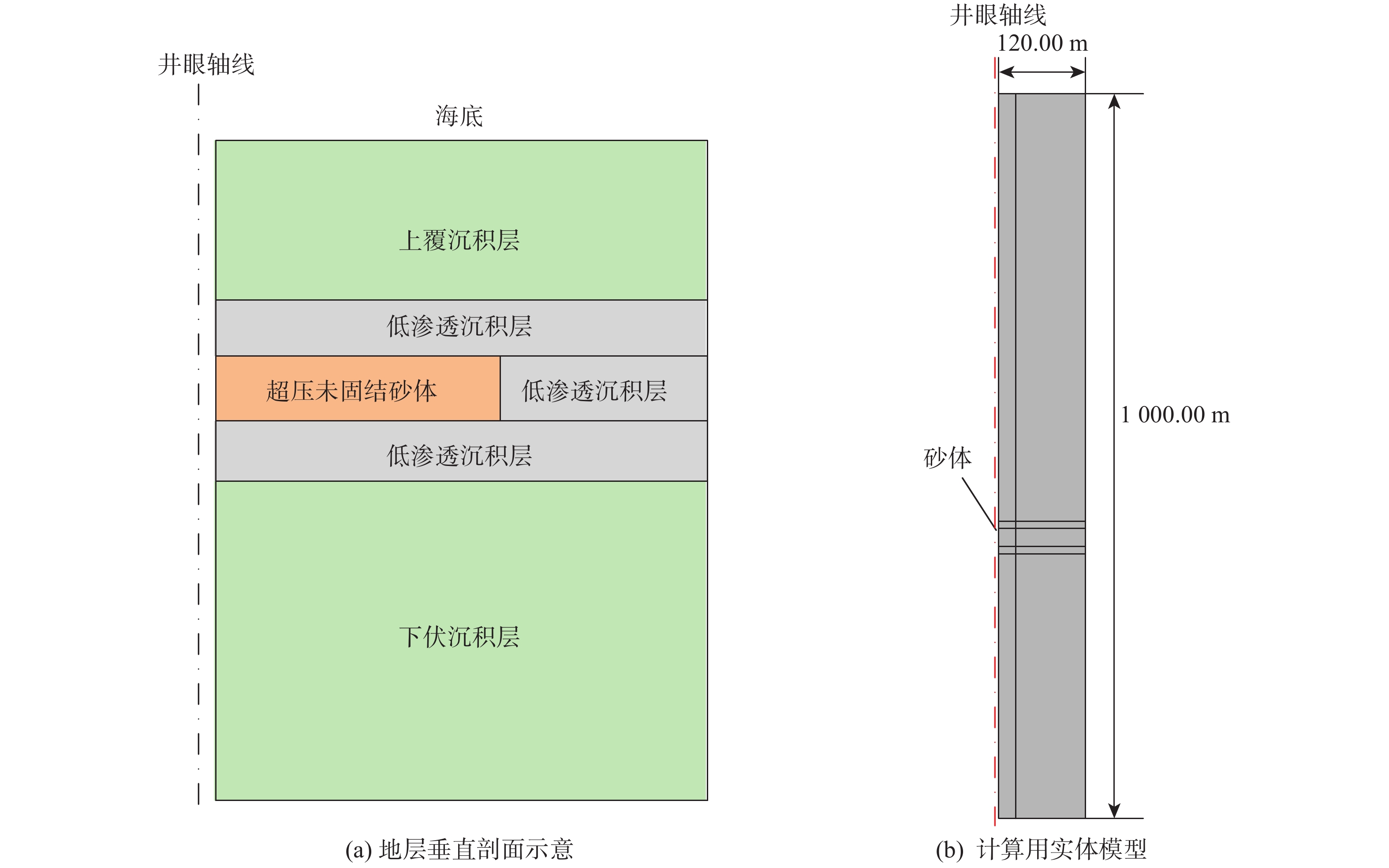
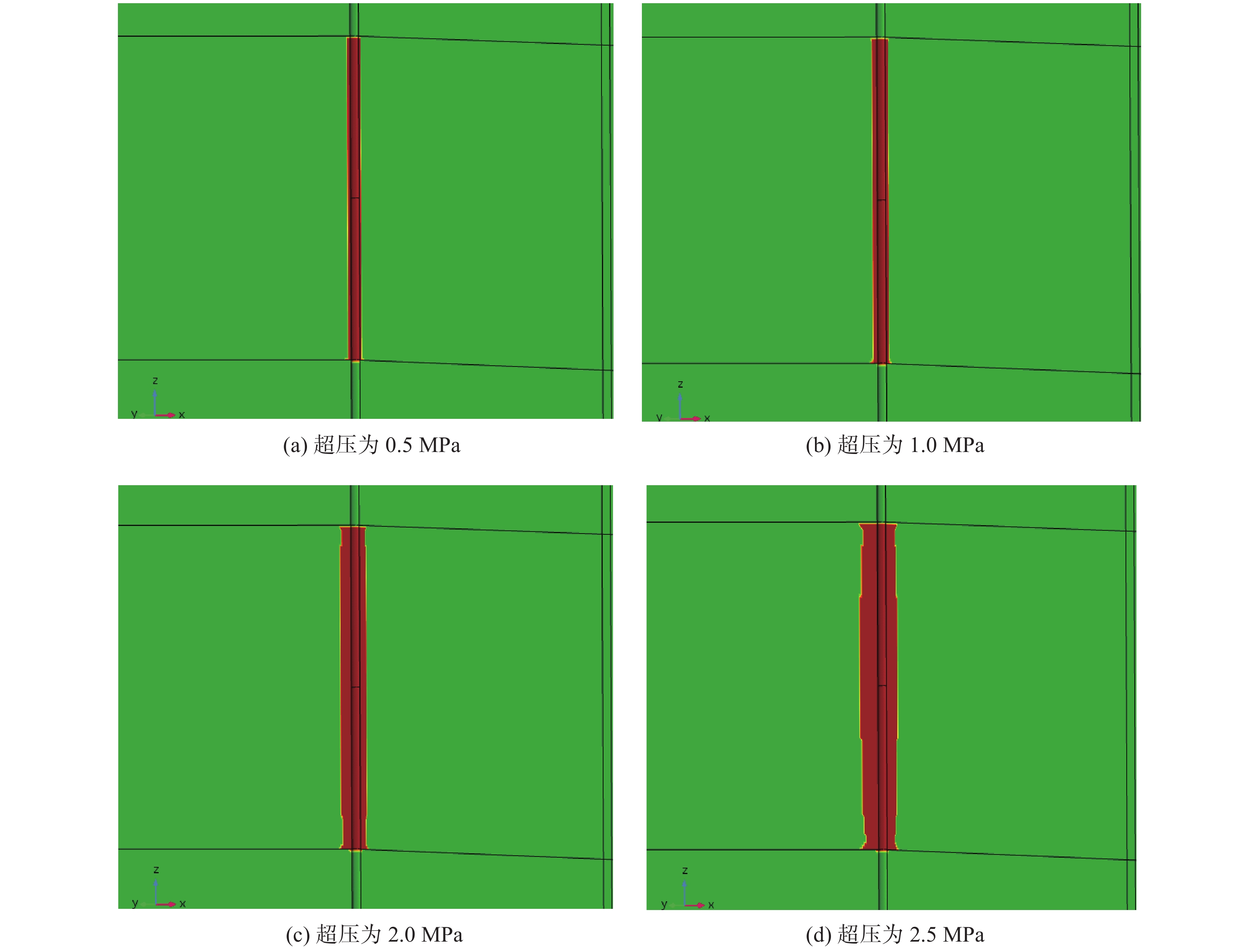
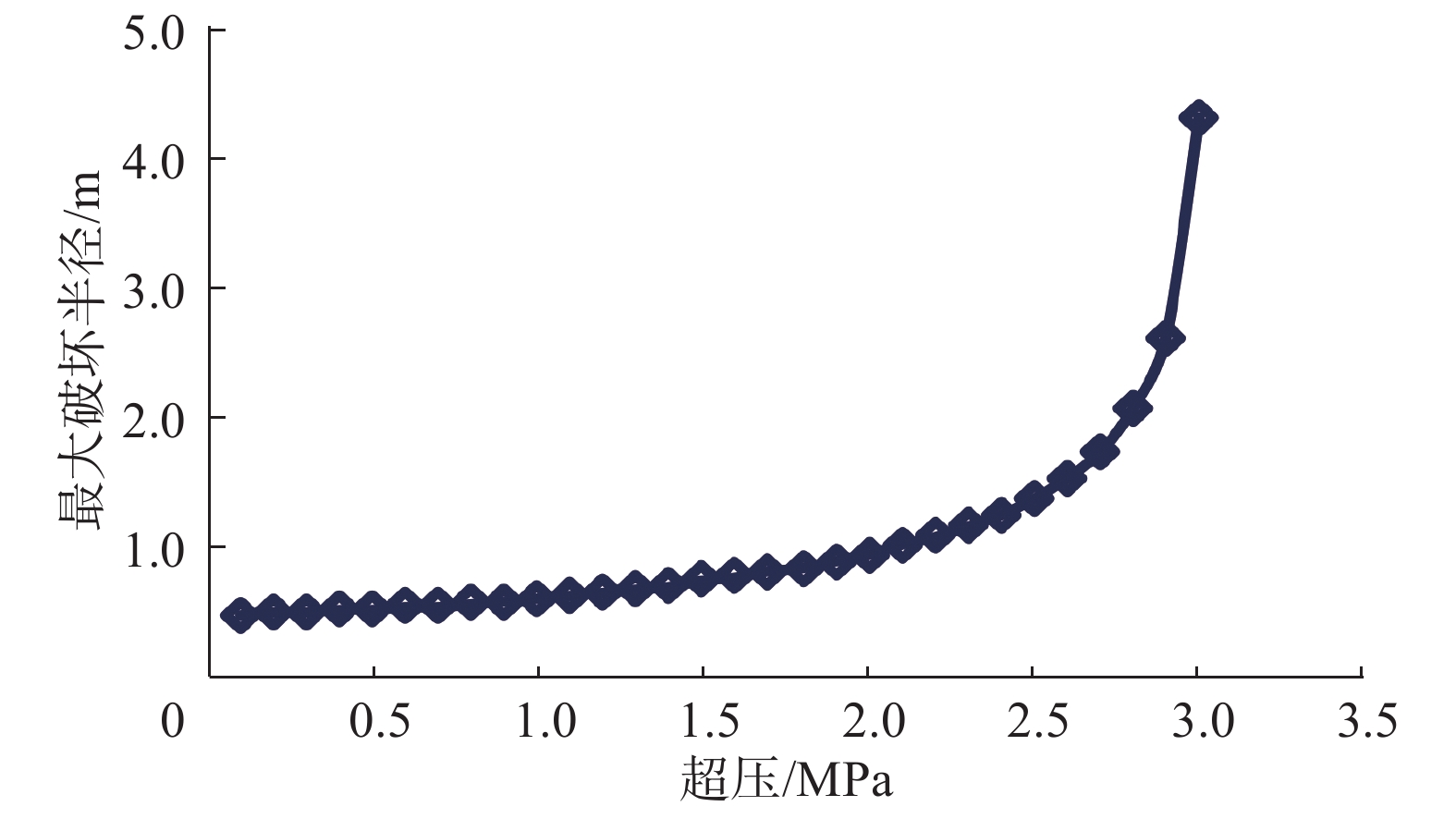
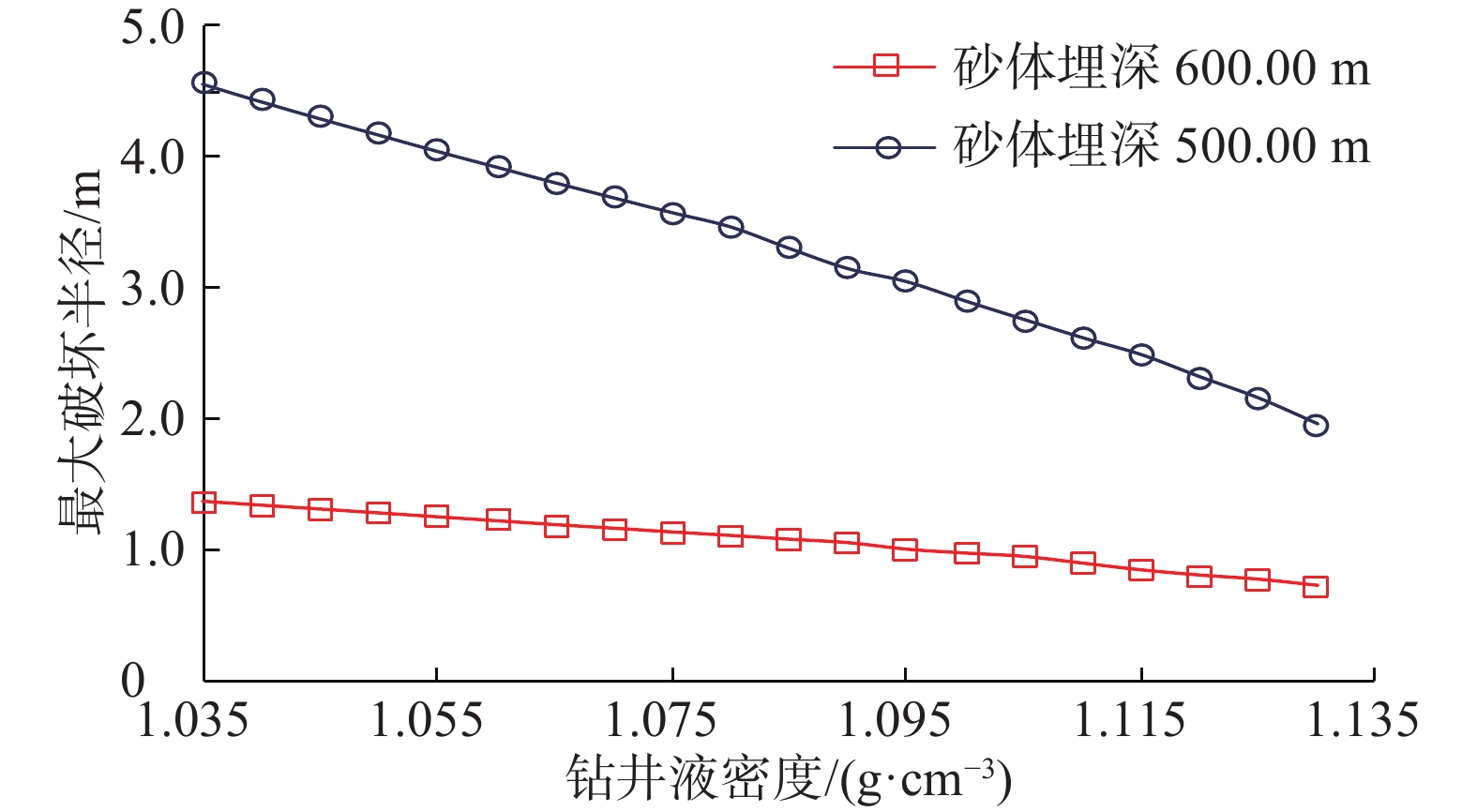
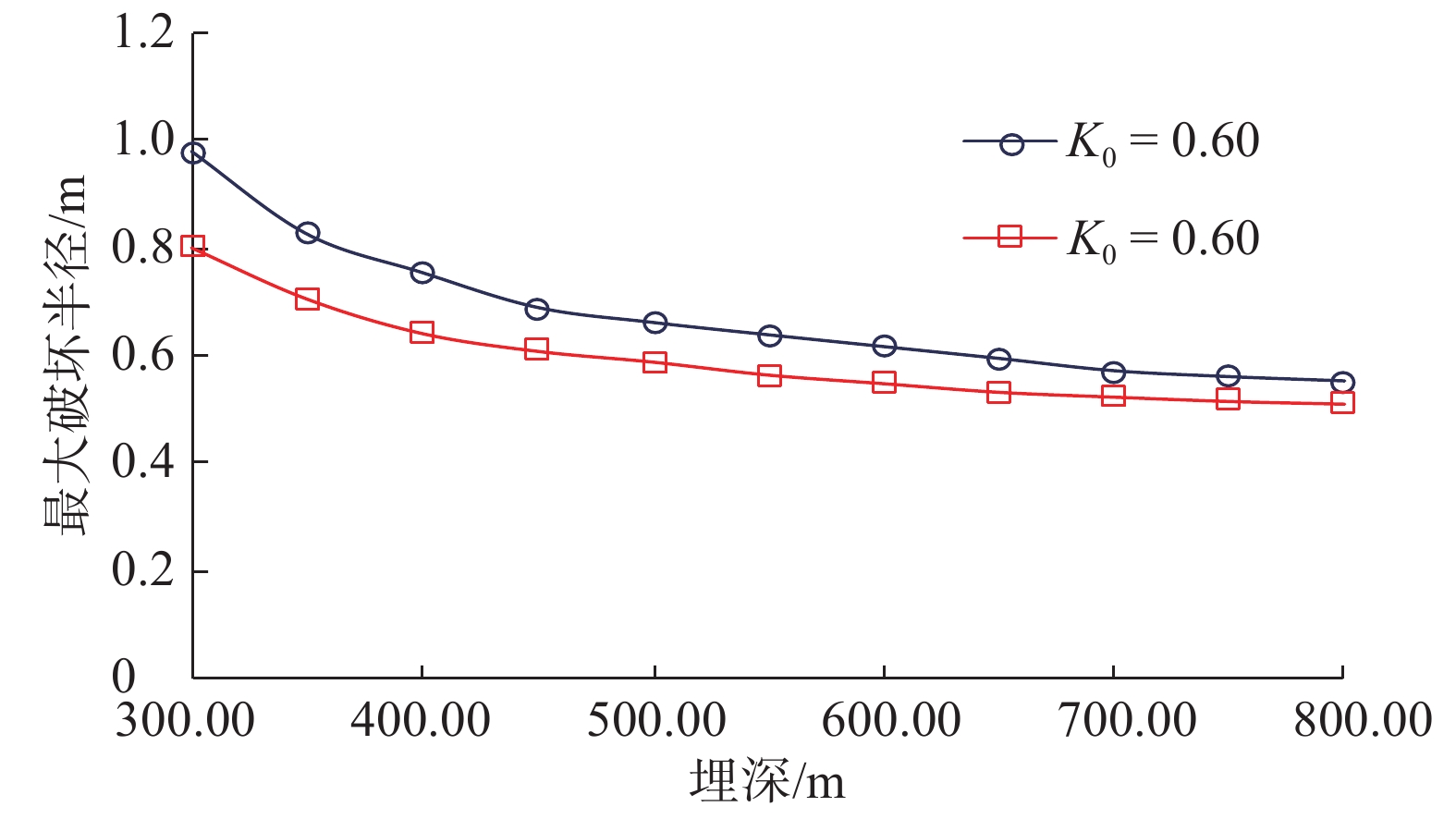
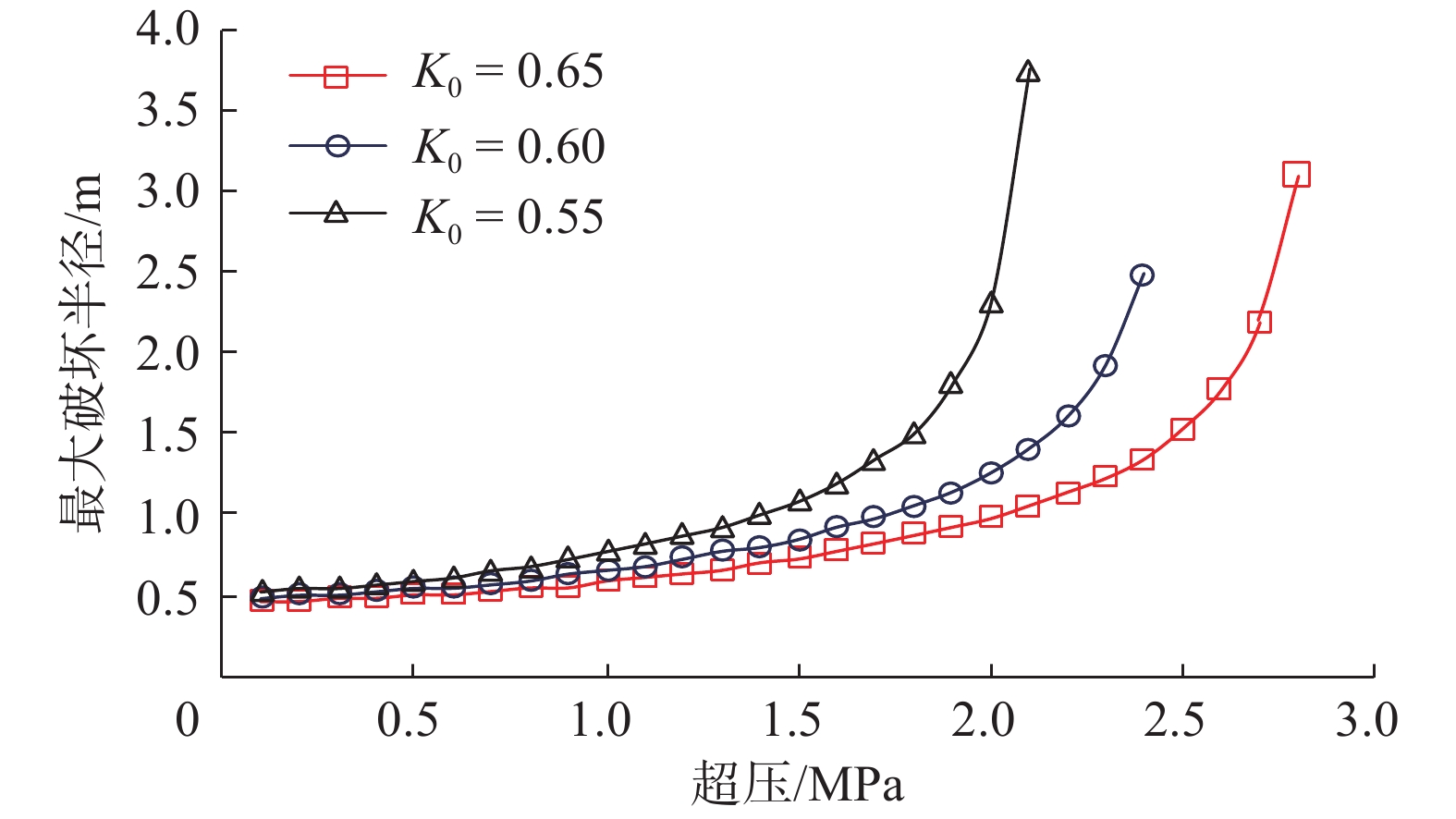
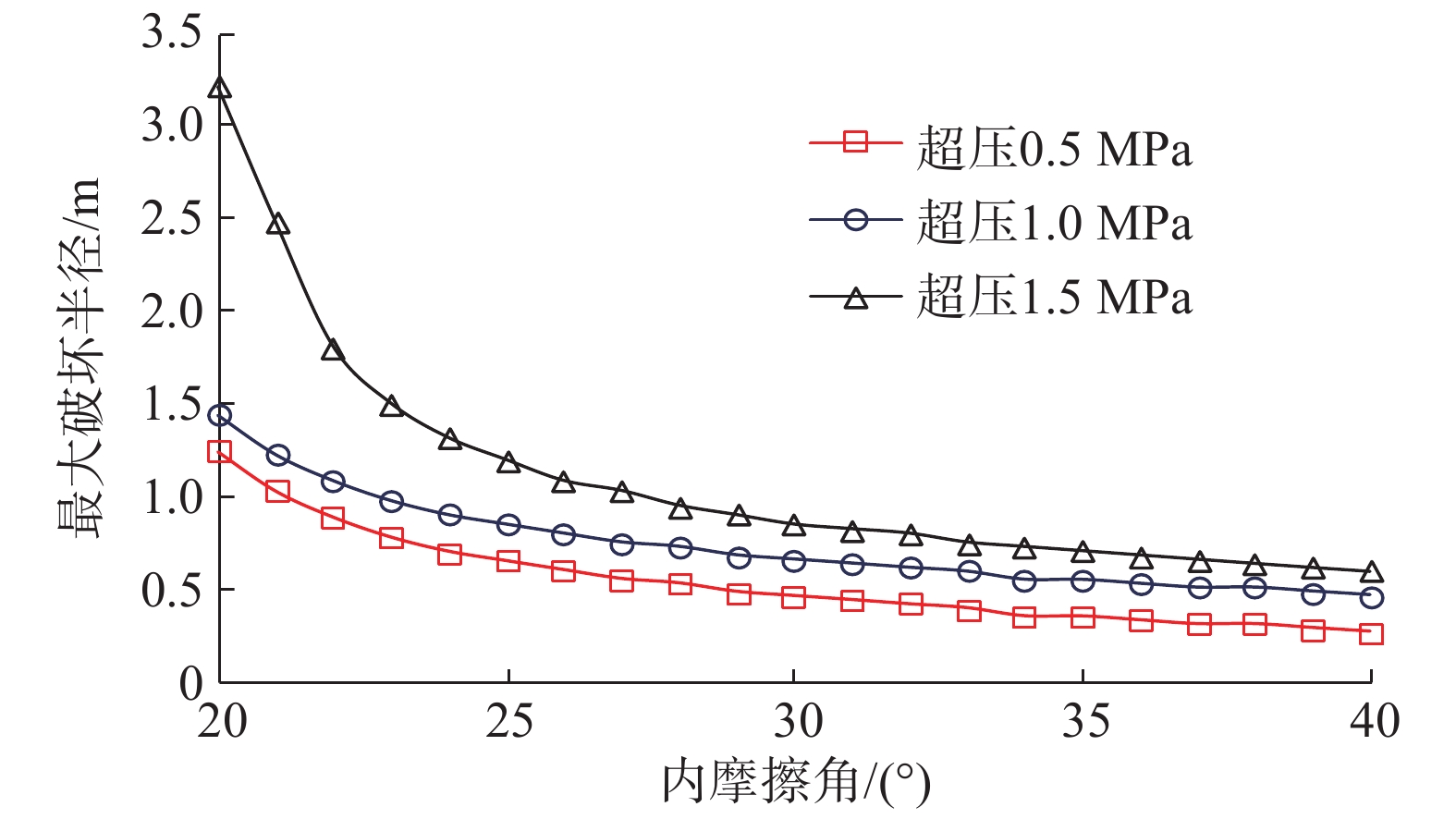
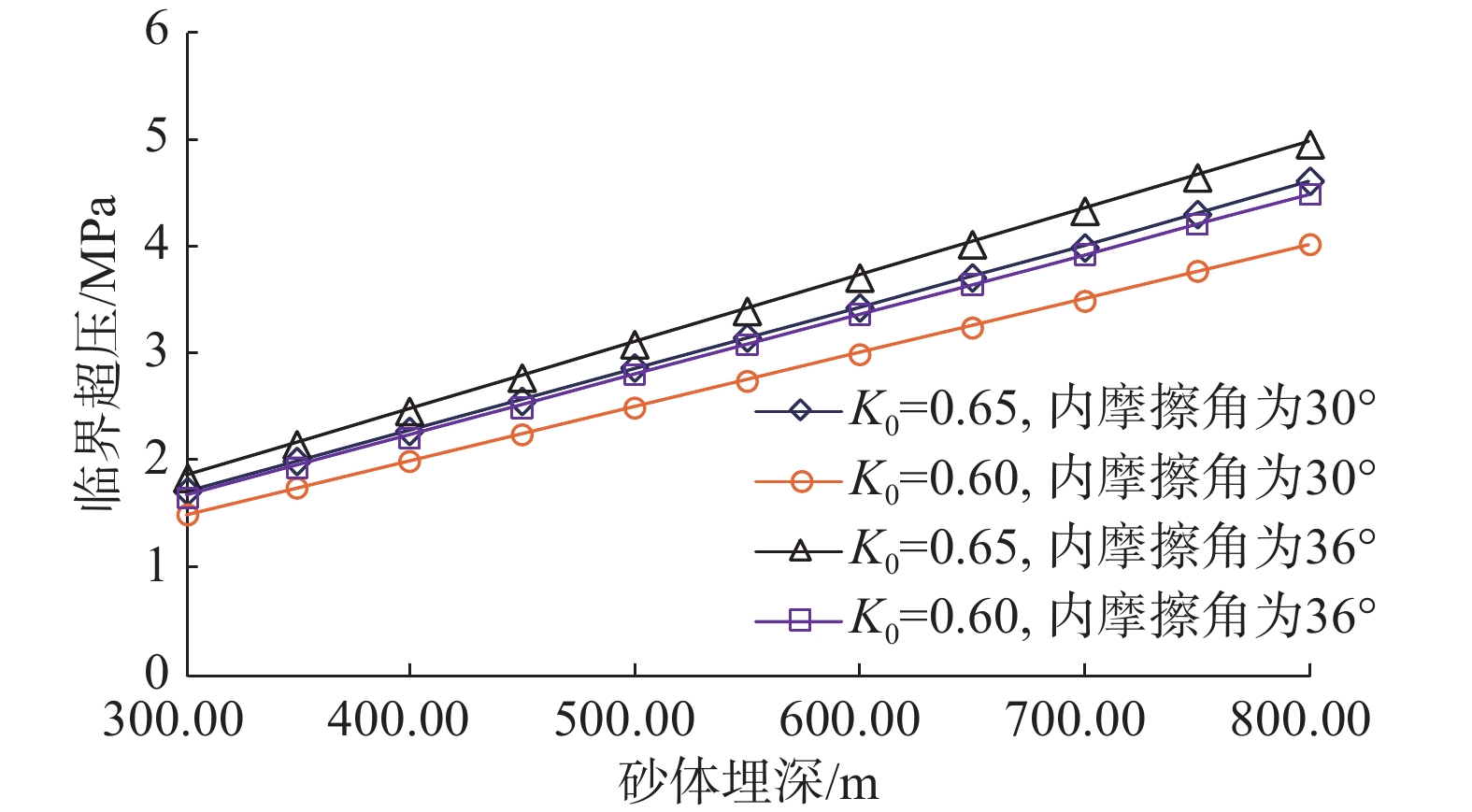
为了定量评价和防治浅水流对深水钻井的危害，进行了浅水流地层井眼坍塌影响因素分析。基于流固耦合理论建立了浅水流地层井眼稳定理论模型，并分别根据Mohr-Coulomb 准则和最大拉应力准则判断砂体的剪切和拉伸破坏，分析了各因素对井周最大破坏半径及砂体临界超压的影响。计算分析发现：超压将导致浅水流地层发生破坏，随着超压增大，其最大破坏半径随之快速增至大；水平有效地应力与垂直有效地应力的比值（K₀）越大，砂体埋深越大，浅水流地层越不容易发生破坏；砂体内摩擦角越大，砂体越稳定；井周最大破坏半径随着钻井液密度升高呈线性递减；浅水流地层存在临界超压，砂体埋深、强度和K₀越大，临界超压越大。研究结果表明，浅水流地层井眼坍塌的风险较大，井周破坏程度与超压、地应力、砂体埋深、钻井液密度和内摩擦角等因素有关，当砂体中的超压超过临界值时，整个砂体都将处于不稳定状态，而提高钻井液密度有利于浅水流地层的稳定。
- 深水钻井 /
- 浅水流 /
- 超压 /
- 流固耦合 /
- 井眼坍塌 /
- 井周破坏 /
- 临界超压
Abstract:
In order to quantitatively evaluate and effectively prevent the damage of shallow water flow during deep water drilling, the contributing factors of wellbore collapse in shallow water flow formations during deep water drilling were analyzed. Based on the fluid-solid coupling theory, the theoretical model of wellbore stability in shallow water flow formation was established. Then they determined the shear and tensile damages of the sand body by the Mohr-Coulomb and maximum tensile stress criteria respectively, as well as analyzed the influence of each factor on maximum damage radius and sand body critical overpressure. The calculation and analysis found that the overpressure would lead to the damage of shallow water flow formation, the maximum damage radius increased rapidly with the increase of overpressure. The greater the ratio of effective horizontal geostress to effective vertical geostress (K₀ ), and the greater the burial depth of sand body, and the less likely the shallow water flow formation is to be damaged; the larger the internal friction angle in the sand body, the more stable the sand body. Likewise, the smaller the internal friction angle, the more significant impact will be. The maximum damage radius around wellbore linearly decreases with the increase of drilling fluid density. There is a relations between critical overpressure found in the shallow water flow. The larger the burial depth, strength and K₀ of sand body, the larger the critical overpressure. The results showed that the risk of wellbore collapse in shallow water flow formation was high. Further, the damage degree around wellbore was related to such factors as overpressure, geostress, sand body depth, drilling fluid density, internal friction angle, etc. When the critical overpressure is exceeded, the entire sand body will be in an unstable state, and the increase of drilling fluid density will be conducive to the wellbore stability in the shallow water flow formation.
- deepwater drilling /
- shallow water flow /
- overpressure /
- fluid-solid coupling /
- wellbore collapse /
- circumferential damage of wellbore /
- critical overpressure

HTML全文

深层干热岩储层具有温度高、硬度大和基质渗透率低等特点，需采用水力压裂等方法改造致密干热岩储层，构建复杂的裂缝网络体系，提高循环工质换热体积，实现高效循环取热^[1–6]。干热岩水力压裂是一个多物理场耦合问题，需要考虑位移、流体压力、温度等多个物理量之间的相互影响^[7–17]。H. Hofmann等人^[18]通过研究发现，复杂裂缝网络有助于提高干热岩储层开采时的经济效益。Zhang Yanjun等人^[19]提出，水平井分段压裂技术可提高循环工质的换热效率，从而提高裂缝型干热岩储层的开采效益。谢紫霄等人^[20]通过干热岩压裂物理模拟试验，发现水力裂缝沟通天然裂缝后能显著提高裂缝渗流系数，实现地热能的高效开发。干热岩储层裂缝扩展过程中受多因素综合影响，且温度影响不容忽略。

相场法是一种基于系统能量最小化原理判断裂缝扩展的有限元方法，在处理多物理场耦合问题时具有网格处理简单、结果准确性高和计算量小等优点，近年来被广泛应用于水力压裂数值模拟领域^[21–26]。侯冰等人^[23]基于相场法建立了流−固−化耦合酸压裂缝扩展模型，分析了孔洞结构对酸压裂缝的影响。N. Noii等人^[25]提出适用于正交各向异性的相场裂缝描述方法，对相场裂缝建模进行了初步分析。

相场法在处理复杂地层多物理场耦合裂缝扩展模拟方面具有显著优势。基于相场法建立了流−固−热耦合裂缝扩展数值模型，采用自适应网格方法平衡计算成本与计算精度，通过解析解验证模拟结果的准确性；在此基础上，研究了干热岩储层水力裂缝的起裂与扩展规律，分析了地质与工程因素对干热岩储层水力裂缝扩展的影响，以期为深层干热岩储层水力压裂提供参考。

1. 深层干热岩储层水力压裂数值模型

基于相场法构建流−固−热耦合裂缝扩展数值模型时，其核心思想是引入无量纲相场参数ϕ描述空间点的物理状态。ϕ的取值在 [0,1]区间，ϕ= 0 表示材料断裂，ϕ= 1 表示材料未断裂， 0 < ϕ < 1 表示材料处于裂缝过渡区域。该参数可以描述裂缝形态，同时可作为指示参数耦合多物理场方程。

1.1 控制方程

1.1.1 相场−位移控制方程

在热弹性多孔介质的相场裂缝模型能量泛函基础上^[24–25]，将裂缝扩展问题转化为系统能量最小化问题并求解，可得相场−位移控制方程强形式：

$\begin{split} - [(1 - k)\phi {\bf{\varepsilon }}({{u}}) - {G_{\mathrm{c}}}\varepsilon \nabla \phi - \frac{{{G_{\mathrm{c}}}}}{\varepsilon }1 - \phi - 2( {{\alpha _{\rm{B}}} } & - 1 )\phi \left( {p - {p_0}} \right) \nabla \cdot {{u}}+ 2\phi \nabla \left( {p - {p_0}} \right){{u}} - 2\left( {{\alpha _{\mathrm{T}}}{K_{\mathrm{d}}} + C} \right)\phi \left( {\theta - {\theta_0}} \right)\nabla \cdot u + \\ & 2C\phi \nabla \left( {\theta - {\theta_0}} \right){{u}}]{\partial _t}\phi = 0\end{split}$

(1)

$\begin{split} - \nabla \cdot [((1 - k){\phi ^2} + k){\sigma ^ + }({{u}}) + {\sigma ^ - }({{u}})] + (\alpha - 1)\nabla ({\phi ^2}p) + {\phi ^2}\nabla p + ({\alpha _{\mathrm{T}}}{K_{\mathrm{d}}} + {C_{\mathrm{T}}})\nabla ({\phi ^2}\theta) + {\phi ^2}\nabla \theta = 0 \end{split}$

(2)

式中：u为位移，m；k为正则化参数；ε(u)为应变；ε为正则化参数；α_B为Biot系数；α_T为热膨胀系数，℃^－1 ；p为流体压力，Pa；p₀为初始压力，Pa； $\theta$ 为温度，℃； $\theta_0$ 为初始温度，℃；C为界面热应力常数，Pa/℃；σ⁺(u)为裂缝驱动力，Pa；σ^－(u)为裂缝非驱动力，Pa；在二维问题中，K_d=μ+λ，μ，λ为Lame系数；G_c为临界能量释放率，Pa·m。

1.1.2 温度场控制方程

基于相场参数的定义，可构建指示函数：

${X}\mathrm{_f}=1-\phi\text{，}{X}_{\mathrm{r}}=\phi$

(3)

基于局部热平衡假设，同一空间点处温度值具有唯一性。引入指示函数后，得到温度场控制方程的有限元强形式：

$\begin{split} {{(}}{{{X}}_{\mathrm{f}}}{C_{\mathrm{f}}} + {{{X}}_{\text{r}}} & {C_{\mathrm{r}}}) \frac{{\partial \theta}}{{\partial t}} = ({{{X}}_{\mathrm{f}}}{K_{\mathrm{f}}} + {{{X}}_{\text{r}}}{K_{\mathrm{r}}})\left[ \frac{\partial }{{\partial x}}\left( {\frac{{\partial \theta}}{{\partial x}}} \right)\right. +\\ & \left. \frac{\partial }{{\partial y}}\left( {\frac{{\partial \theta}}{{\partial y}}} \right) \right] +v\nabla \theta + {Q_{\mathrm{i}}}\end{split}$

(4)

式中：C_f为压裂液热容，kJ·m³/℃ ；C_r为储层热容，kJ·m³/℃ ；K_f为压裂液热传导系数，W/(m·℃)；K_r为地层岩石热传导系数，W/(m·℃)； v为流体流速，m/s；Q_i为注入热源，J。

1.1.3 流体压力控制方程

对于流体场，其物质守恒方程为：

$\partial_t\left(\rho\mathrm{_f}\varphi^*\right)+\nabla\cdot\left(\rho_{\mathrm{f}}v\right)=q$

(5)

式中：ρ_f为液体密度，g/cm³；φ^*为孔隙度；q为单位时间内注入的压裂液质量，g。

计算流体流速时忽略重力影响，表达式为：

$v = - \frac{K}{\eta }\Delta p$

(6)

式中：K为渗透率，D；η为液体黏度，mPa·s。

$\varphi^*=\varphi_0^*+\alpha\mathrm{_B}\nabla\cdot u+\frac{1}{M}(p-p_0)+K\mathrm{_T}(\theta -\theta_0)$

(7)

式中： $\varphi_0^*$ 为初始时刻孔隙度；M为Biot系数；K_T为孔隙热膨胀系数，℃⁻¹。

流体压力控制方程的强形式为：

$\rho\mathrm{_f}\partial_t\left(\alpha_{\mathrm{B}}\nabla\cdot u+\frac{1}{M}p+K_{\mathrm{T}}\theta \right)-\rho_{\mathrm{f}}\frac{K}{\eta}\nabla\cdot\Delta p=q$

(8)

1.2 自适应网格

模型中以相场参数为指示参数，引入自适应网格技术，在保证模拟精度的前提下，减少模型的计算量。自适应网格算法流程如图1所示。

图 1 自适应网格处理流程

Figure 1. Adaptive mesh processing procedure

下载: 全尺寸图片幻灯片

自适应网格可对同一时间步内的裂缝扩展状态进行多次求解，但与全局细分网格相比节点数量少、计算简单，计算精度仍保持良好^[26]。

1.3 多物理场耦合求解

模型共包括固体场模块、温度场模块和流体场模块等3个模块，模型中包括4个解变量，分别为相场参数（ϕ）、位移（u）、温度（T）和流体压力（p）。在固体场模块中，采用全耦合方法求解相场参数与位移；利用温度场模块、流体场模块分别求解温度和压力值，并采用固定应力迭代的方式与固体场耦合。具体流程如下：

1）在任意时间步tⁿ⁺¹，给定上一个时间步的解θⁿ，uⁿ，ϕⁿ和pⁿ。

2）基于固定应力法，构建迭代序列l=0，1，2…，定义初始解变量u_l₌₀=uⁿ，ϕ_l₌₀=ϕⁿ，p_l₌₀=pⁿ，θ_l₌₀=θⁿ。

3）给定θⁿ，uⁿ，ϕⁿ，pⁿ，u_l，ϕ_l和p_l，求解式（4），得到θ_l₊₁。

4）给定θⁿ，uⁿ，ϕⁿ，pⁿ，u_l，ϕ_l和θ_l，求解式（8）获得p_l₊₁。

5）给定θⁿ，uⁿ，ϕⁿ，pⁿ，p_l和θ_l，求解式（1）和式（2），可得{u_l₊₁，ϕ _l₊₁}。

6）若max{||p_l+1−p_l||，||θ_l+1−|θ_l||，||u_l+1−u_l||，||ϕ_l+1−ϕ_l||}≤TOL_fs，则迭代收敛（TOL_fs为固定应力法容差，取10^－8），令pⁿ⁺¹=p_l+1，θⁿ⁺¹=θ_l+1，uⁿ⁺¹=u_l+1，ϕⁿ⁺¹=ϕ_l+1；若迭代不收敛，则令u_l+1=u_l，ϕ_l+1=ϕ_l，p_l+1=p_l，θ_l+1=θ_l，重复步骤3）—5），直至满足收敛条件。

7）检查网格系统是否满足计算精度要求，若不满足，则更新自适应网格系统。

8）输出θⁿ⁺¹，uⁿ⁺¹， ϕⁿ⁺¹和pⁿ⁺¹作为时间步tⁿ⁺¹的解变量，并进行下一个时间步的计算。

1.4 初始条件与边界条件

模拟二维条件下的裂缝扩展过程，忽略重力影响与垂向应变。模型初始状态及边界条件如图2所示。

图 2 相场裂缝模型初始状态

Figure 2. Initial condition of phase-field fracture model

下载: 全尺寸图片幻灯片

模型长30 cm，宽30 cm。设置天然裂缝等结构时，将对应位置相场参数固定为0，其余岩石基质区域处相场参数设置为1，进行模拟分析，根据相场参数判断裂缝扩展情况。设定压裂液温度为20 ℃，岩石弹性模量为40 GPa，泊松比为0.20，岩石密度为2.50 g/cm³，Biot系数为0.80，渗透率为1 mD，地层岩石热容为2.0 MJ·m³/℃ ，压裂液热容4.2 MJ·m³/℃ ，地层岩石热传导系数为0.63 W/(m·℃)。

1.5 解析解验证

相场裂缝模型中，最小网格尺寸受网格细分次数控制。采用自适应网格方法，全局细分5次、局部细分3次时，最小网格尺寸为1.17 mm；采用全局网格细分方法，全局细分8次时，最小网格尺寸同样为1.17 mm。固定边界位移，分别采用全局细分网格与自适应网格对裂缝扩展进行模拟，模拟结果如图3所示。

图 3 固定边界位移条件下干热岩水力压裂数值模拟

Figure 3. Numerical simulation of hydraulic fracturing in HDR reservoir under fixed boundary displacement

下载: 全尺寸图片幻灯片

无限大线弹性物体内有一条缝内压力均匀分布的裂缝，其裂缝宽度的计算公式为^[27]：

$w = \frac{{4\left( {1 - {\nu ^2}} \right){p_{\text{f}}}}}{E}\sqrt {{c^2} - {y^2}}$

(9)

式中：w为裂缝宽度，mm；p_f 为裂缝内流体压力，Pa；c为裂缝半缝长，mm；y为裂缝内某点到裂缝中心点的距离，mm； $\nu$ 为岩石泊松比；E为岩石弹性模量，GPa。

将流体压力代入式（9），计算裂缝宽度解析解，并与不同网格方案下裂缝宽度对比，结果如图4所示。

图 4 沿y轴方向缝宽分布情况

Figure 4. Fracture width distribution along y-axis direction

下载: 全尺寸图片幻灯片

模拟结果表明，裂缝宽度的数值解与解析解吻合程度较好，自适应网格与全局细分网格的模拟结果相接近。自适应网格方法节点少，算力消耗低，计算相场裂缝模型时有显著优势。

2. 地质与工程因素对裂缝扩展的影响

2.1 温度

温度场的变化会造成岩石体积变化，在系统内部互相约束，从而产生热应力^[28–29]。为研究温度对水力裂缝起裂与扩展的影响，设置初始地层温度分别为20，100和200 ℃，压裂液注入温度均为20 ℃，排量均为20 mL/min，边界应力分别为10和7 MPa，裂缝长度变化趋势如图5所示。

图 5 不同地层温度下干热岩储层水力压裂缝长变化趋势

Figure 5. Variation trend of hydraulic fracture length in HDR reservoir with different formation temperature

下载: 全尺寸图片幻灯片

模拟过程中，由于压裂液温度低于地层温度，热应力呈现为拉应力，且地层温度越高，热应力越大；由于水力裂缝以拉伸缝为主，热应力在裂缝扩展过程中起辅助作用。压裂液排量相同时，地层温度越高，裂缝扩展速度越快，起裂压力越低。真实干热岩储层中，岩石不同矿物热膨胀时存在各向异性，热应力方向与大小更为复杂，更容易产生局部应力集中；若地层中微裂缝发育，热应力易激活并诱导微裂缝起裂，提高水力裂缝复杂程度，且热应力越大，微裂缝激活程度越高。

2.2 压裂液排量

为探究不同压裂液排量对水力裂缝扩展的影响，设置压裂液排量分别为10，20和30 mL/min，地层初始温度均为200 ℃，压裂液温度均为20 ℃，边界应力分别为10和7 MPa，注液30 s后，模拟结果如图6所示。

图 6 不同压裂液排量下干热岩储层水力压裂模拟结果

Figure 6. Simulation results of hydraulic fracturing in HDR reservoir under different pumping rates of fracturing fluids

下载: 全尺寸图片幻灯片

从图6可以看出，压裂液排量为10 mL/min时，缝长为11.63 cm；压裂液排量为20 mL/min时，缝长为20.26 cm；压裂液排量为30 mL/min时，缝长为27.48 cm。研究表明，随着压裂液排量增加，液体憋压速度更快，裂缝周边岩石温度降低更明显。干热岩储层水力裂缝扩展受流体压力和热应力的共同驱动，裂缝扩展速度更快，裂缝宽度也随之增大，更有利于后续循环介质的注入与热交换。

2.3 天然裂缝夹角

为探究天然裂缝对水力裂缝扩展的影响，设置天然裂缝与水平最大主应力方向的夹角分别为90°，45°和20°，地层初始温度均为200 ℃，压裂液温度均为20 ℃，压裂液排量为20 mL/min，边界应力分别为10和7 MPa，模拟结果如图7所示。

图 7 不同天然裂缝夹角下干热岩储层水力压裂模拟结果

Figure 7. Simulation results of hydraulic fracturing in HDR reservoir with different angles of natural fractures

下载: 全尺寸图片幻灯片

水力压裂裂缝起裂后沿水平最大主应力方向扩展，遇到天然裂缝后发生转向并沟通天然裂缝。天然裂缝与水平最大主应力方向夹角为90°时，水力裂缝转向不明显，沟通天然裂缝后在天然裂缝两侧同时起裂并扩展，扩展角度与最大水平地应力夹角约为45°，2条裂缝呈分离趋势。岩石温度在水力压裂裂缝与天然裂缝沟通处降幅较大，主要原因为压裂液在该区域流动情况更复杂，传热效率高。

天然裂缝与水平最大主应力方向夹角为45°时，水力裂缝转向效果较明显，沟通天然裂缝后在天然裂缝两侧起裂并扩展，左右两侧扩展速度差异明显，左侧扩展速度更快，这是因为该侧与水平最大主应力方向夹角较小，扩展速度更快。另外，岩石温度在水力裂缝与天然裂缝右侧夹角处降低幅度较大，主要是该侧天然裂缝与水力压裂裂缝距离较近，传热效率更高。

天然裂缝与水平最大主应力方向夹角为20°时，天然裂缝诱导水力压裂裂缝产生转向现象。水力压裂裂缝沟通天然裂缝后在天然裂缝两侧起裂并扩展，左右两侧扩展速度差异明显，左侧扩展速度更快，裂缝沿水平最大主应力方向继续扩展。岩石温度在水力压裂裂缝与天然裂缝右侧夹角处降低幅度较大。

基于上述模拟结果可知，水力压裂裂缝遇到天然裂缝后易沟通天然裂缝，天然裂缝与水平最大主应力夹角越小，转向现象越明显。水力压裂裂缝与天然裂缝沟通位置流动情况复杂，传热效率高。水力压裂裂缝再次起裂方向受到地应力与天然裂缝方向的共同作用，在水平最大主应力方向夹角较小的方向扩展迅速，在水平最大主应力方向夹角较大的方向扩展较慢，且该侧岩石降温幅度更大。

2.4 多天然裂缝干扰下裂缝扩展

为探究多天然裂缝干扰下干热岩储层水力裂缝扩展力学行为，设置不同地应力与排量进行模拟。单侧天然裂缝条数为2条，天然裂缝与水平最大主应力方向夹角为45°，地层初始温度为200 ℃，压裂液温度为20 ℃，压裂液排量分别为20 和50 mL/min，边界应力差分别为3和8 MPa，模拟结果如图8所示。

图 8 不同天然裂缝密度下干热岩储层水力压裂模拟结果

Figure 8. Simulation results of hydraulic fracturing in HDR reservoir with different densities of natural fractures

下载: 全尺寸图片幻灯片

地层中存在多条天然裂缝时，水力压裂裂缝优先与距离最近的天然裂缝发生相互作用。地应力差为3 MPa、压裂液排量为20 mL/min时，水力压裂裂缝在靠近天然裂缝时轻微转向并开启初条天然裂缝，随后在天然裂缝尖端二次起裂；地应力差为8 MPa、压裂液排量为20 mL/min时，水力压裂裂缝靠近天然裂缝无明显转向现象，开启初条天然裂缝后在裂缝尖端二次起裂；地应力差为8 MPa、压裂液排量增加至50 mL/min时，水力压裂裂缝贯穿初条天然裂缝并继续扩展，由于水力压裂裂缝贯穿天然裂缝后会消耗水力能量，因此仅能贯穿单条天然裂缝。

3. 结　论

1）基于相场法建立了流−固−热多场耦合裂缝扩展数值模型，根据能量最小化原理计算裂缝形态，无需额外添加裂缝扩展准则，模型搭建简单，可用于干热岩储层水力裂缝扩展模拟研究。

2）干热岩储层水力压裂过程中，热应力体现为拉应力，有助于增加裂缝开度，在裂缝扩展过程中起辅助作用。压裂液与地层温度差越高，排量越大，热应力影响效果越显著；若地层中微裂缝发育，热应力易激活并诱导微裂缝起裂，提高水力压裂裂缝的复杂程度。

3）地层中存在多条天然裂缝时，水力压裂裂缝优先与距离最近的天然裂缝发生相互作用。水力压裂裂缝遇到天然裂缝后易沟通天然裂缝，天然裂缝与水平最大主应力方向夹角越小，地应力差越小，转向现象越明显。水力压裂裂缝再次起裂时沿天然裂缝方向起裂，且向水平最大主应力方向偏转。

图 1 地层垂直剖面及相应的有限元实体模型

Figure 1. Stratigraphic vertical section and corresponding solid model

下载: 全尺寸图片幻灯片

图 2 不同超压下浅水流地层井周破坏情况

Figure 2. The damage around wellbore in shallow water flow formation under different overpressures

下载: 全尺寸图片幻灯片

图 3 不同超压下的井周最大破坏半径

Figure 3. The maximum damage radius around wellbore under different overpressures

下载: 全尺寸图片幻灯片

图 4 井周最大破坏半径随钻井液密度的变化

Figure 4. Variation of the maximum damage radius around wellbore with the density of drilling fluid

下载: 全尺寸图片幻灯片

图 5 不同砂体中部埋藏深度下的井周最大破坏半径

Figure 5. The maximum damage radius around wellbore at middle depth under the different sand body

下载: 全尺寸图片幻灯片

图 6 不同K₀下浅水流地层的井周最大破坏半径随超压大小的变化

Figure 6. The variation of the maximum damage radius around wellbore in the shallow water flow formation with the overpressure under different K₀

下载: 全尺寸图片幻灯片

图 7 不同内摩擦角下的浅水流地层井周最大破坏半径

Figure 7. The maximum damage radius around wellbore in the shallow water flow formation under different internal friction angles

下载: 全尺寸图片幻灯片

图 8 不同内摩擦角和K₀时临界超压随砂体埋深的变化

Figure 8. Variation curves of critical overpressure with sand body burial depth under different internal friction angles and K₀

下载: 全尺寸图片幻灯片

图 9 不同埋深和K₀时临界超压随砂体内摩擦角的变化

Figure 9. Variation curves of critical overpressure with the internal friction angle of sand body under different burial depths and K₀

下载: 全尺寸图片幻灯片

图 10 不同砂体埋深和内摩擦角时临界超压随K₀的变化

Figure 10. Variation curves of critical overpressure with K₀ under different burial depths and internal friction angles in sand bodies

下载: 全尺寸图片幻灯片

参考文献(20)

[1]	孙宝江, 张振楠. 南海深水钻井完井主要挑战与对策[J]. 石油钻探技术, 2015, 43(4): 1–7. SUN Baojiang, ZHANG Zhennan. Challenges and countermeasures for the drilling and completion of deepwater wells in the South China Sea[J]. Petroleum Drilling Techniques, 2015, 43(4): 1–7.
[2]	CUNDIFF L W, DAUGHERTY B, MIX K. Case study: statistical risk to a drill center from shallow-water flow[J]. Journal of Petroleum Technology, 2005, 57(3): 64–67. doi: 10.2118/0305-0064-JPT
[3]	BRUCE R, MCKEOWN J, SARGENT T, et al. Mitigating the shallow water flow risk at Mississippi canyon 849: a team approach[R]. OTC 15249, 2003.
[4]	OSTERMEIER R M, PELLETIER J H, WINKER C D, et al. Dealing with shallow-water flow in the deepwater Gulf of Mexico[R]. OTC 11972, 2000.
[5]	PUTANS V, MERKLIN L R, LEVCHENKO O V. Sediment waves and other forms as evidence of geohazards in Caspian Sea[J]. International Journal of Offshore & Polar Engineering, 2010, 20(4): 241–246.
[6]	ALBERTY M W, HAFLE M E, MINGE J C, et al. Mechanisms of shallow water flows and drilling practices for intervention[J]. SPE Drilling & Completion, 1999, 14(2): 123–129.
[7]	FULLER G A, BOLADO D L, HARDY F. A Gulf of Mexico case history: benefits of foamed cementing to combat a SWF[R]. SPE 128160, 2010.
[8]	叶志, 樊洪海, 张国斌, 等. 深水钻井地质灾害浅层水流问题研究[J]. 石油钻探技术, 2010, 38(6): 48–52. doi: 10.3969/j.issn.1001-0890.2010.06.011 YE Zhi, FAN Honghai, ZHANG Guobin, et al. Investigation of shallow water flow in deepwater drilling[J]. Petroleum Drilling Techniques, 2010, 38(6): 48–52. doi: 10.3969/j.issn.1001-0890.2010.06.011
[9]	MALLICK S, DUTTA N C. Shallow water flow prediction using prestack waveform inversion of conventional 3D seismic data and rock modeling[J]. The Leading Edge, 2002, 21(7): 675–680. doi: 10.1190/1.1497323
[10]	DENNEY D. Shallow-water-flow prediction from multicomponent seismic data[J]. Journal of Petroleum Technology, 2000, 52(7): 34–36. doi: 10.2118/0700-0034-JPT
[11]	MUKERJI T, DUTTA N, PRASAD M, et al. Seismic detection and estimation of overpressure: part Ⅰ: the rock physics basis[J]. CSEG Recorder, 2002, 27(7): 34–57.
[12]	ZIMMER M, PRASAD M, MAVKO G. Pressure and porosity influences on Vp-Vs ratio in unconsolidated sands[J]. The Leading Edge, 2002, 21(2): 178–183. doi: 10.1190/1.1452609
[13]	吴时国, 孙运宝, 王秀娟, 等. 南海北部深水盆地浅水流的地球物理特性及识别[J]. 地球物理学报, 2010, 53(7): 1681–1690. doi: 10.3969/j.issn.0001-5733.2010.07.019 WU Shiguo, SUN Yunbao, WANG Xiujuan, et al. Geophysical signature and detection of shallow water flow in the deepwater basin of the Northern South China Sea[J]. Chinese Journal of Geophysics, 2010, 53(7): 1681–1690. doi: 10.3969/j.issn.0001-5733.2010.07.019
[14]	任韶然, 宫智武, 张亮, 等. 南海北部陆坡浅水流评估及深水钴井防治措施[J]. 中国石油大学学报(自然科学版), 2017, 41(4): 99–106. doi: 10.3969/j.issn.1673-5005.2017.04.013 REN Shaoran, GONG Zhiwu, ZHANG Liang, et al. Shallow water flow hazard assessment in the northern slope of the South China Sea and control measures during deepwater drilling[J]. Journal of China University of Petroleum(Edition of Natural Science), 2017, 41(4): 99–106. doi: 10.3969/j.issn.1673-5005.2017.04.013
[15]	李广信, 周晓杰. 土的渗透破坏及其工程问题[J]. 工程勘察, 2004(5): 10–13, 52. LI Guangxin, ZHOU Xiaojie. Seepage failure of soil and related engineering problems[J]. Geotechnical Investigation & Surveying, 2004(5): 10–13, 52.
[16]	SUN Jin, DENG Jingen, YU Baohua, et al. Model for fracture initiation and propagation pressure calculation in poorly consolidated sandstone during waterflooding[J]. Journal of Natural Gas Science and Engineering, 2015, 22: 279–291. doi: 10.1016/j.jngse.2014.12.004
[17]	BENMEBAREK N, BENMEBAREK S, KASTNER R. Numerical studies of seepage failure of sand within a cofferdam[J]. Computers and Geotechnics, 2005, 32(4): 264–273. doi: 10.1016/j.compgeo.2005.03.001
[18]	孙运宝, 赵铁虎, 秦柯. 南海北部白云凹陷沉积压实作用对浅水流超压演化影响数值模拟[J]. 地球科学进展, 2014, 29(9): 1055–1064. SUN Yunbao, ZHAO Tiehu, QIN Ke. Numerical simulation of overpressure of shallow water flow in Baiyun Sag of the Northern South China Sea[J]. Advances in Earth Science, 2014, 29(9): 1055–1064.
[19]	OSTERMEIER R M, PELLETIER J H, WINKER C D, et al. Trends in shallow sediment pore pressures: deepwater Gulf of Mexico[R]. SPE 67772, 2001.
[20]	陈仲颐, 周景星, 王洪瑾．土力学[M]．北京: 清华大学出版社, 1994: 46-47． CHEN Zhongyi, ZHOU Jingxing, WANG Hongjin. Soil mechanics [M]. Beijing: Tsinghua University Press, 1994: 46-47.

施引文献(9)

期刊类型引用(4)

1.	陈德春，张文宣，阳成，常峰，邴绍强，张鹏，王亮亮，马硕. 基于井口流体温度的含水率计算模型. 断块油气田. 2025(03): 514-521 . 百度学术
2.	魏锋，陈现，王迪，夏瑜. 海上少井条件下含水率计算方法研究及应用. 海洋石油. 2022(04): 63-66 . 百度学术
3.	王谦，谭茂金，石玉江，李高仁，程相志，罗伟平. 径向基函数神经网络法致密砂岩储层相对渗透率预测与含水率计算. 石油地球物理勘探. 2020(04): 864-872+704 . 百度学术
4.	王谦，石玉江，谭茂金，李高仁. 基于孔隙结构分类的致密砂岩含水率计算模型——以鄂尔多斯盆地陇东西部延长组长8_1储层为例. 石油物探. 2019(05): 669-680 . 百度学术

其他类型引用(5)

资源附件(0)

图(10)

计量

文章访问数: 3601
HTML全文浏览量: 2120
PDF下载量: 57
被引次数: 9

1. 深层干热岩储层水力压裂数值模型
1.1 控制方程
1.1.1 相场−位移控制方程
1.1.2 温度场控制方程
1.1.3 流体压力控制方程
1.2 自适应网格
1.3 多物理场耦合求解
1.4 初始条件与边界条件
1.5 解析解验证
2. 地质与工程因素对裂缝扩展的影响
2.1 温度
2.2 压裂液排量
2.3 天然裂缝夹角
2.4 多天然裂缝干扰下裂缝扩展
3. 结　论

1. 深层干热岩储层水力压裂数值模型
1.1 控制方程
1.1.1 相场−位移控制方程
1.1.2 温度场控制方程
1.1.3 流体压力控制方程
1.2 自适应网格
1.3 多物理场耦合求解
1.4 初始条件与边界条件
1.5 解析解验证
2. 地质与工程因素对裂缝扩展的影响
2.1 温度
2.2 压裂液排量
2.3 天然裂缝夹角
2.4 多天然裂缝干扰下裂缝扩展
3. 结　论

参考文献(20)

施引文献(9)

资源附件(0)

深水钻井浅水流地层井眼坍塌影响因素分析

计量

出版历程