Wellbore Stability Evaluation during Gas Drilling through Low Permeability Gas Reservoirs in Western Sichuan
-
摘要:
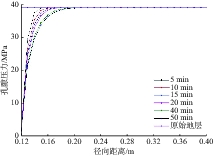
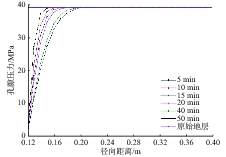
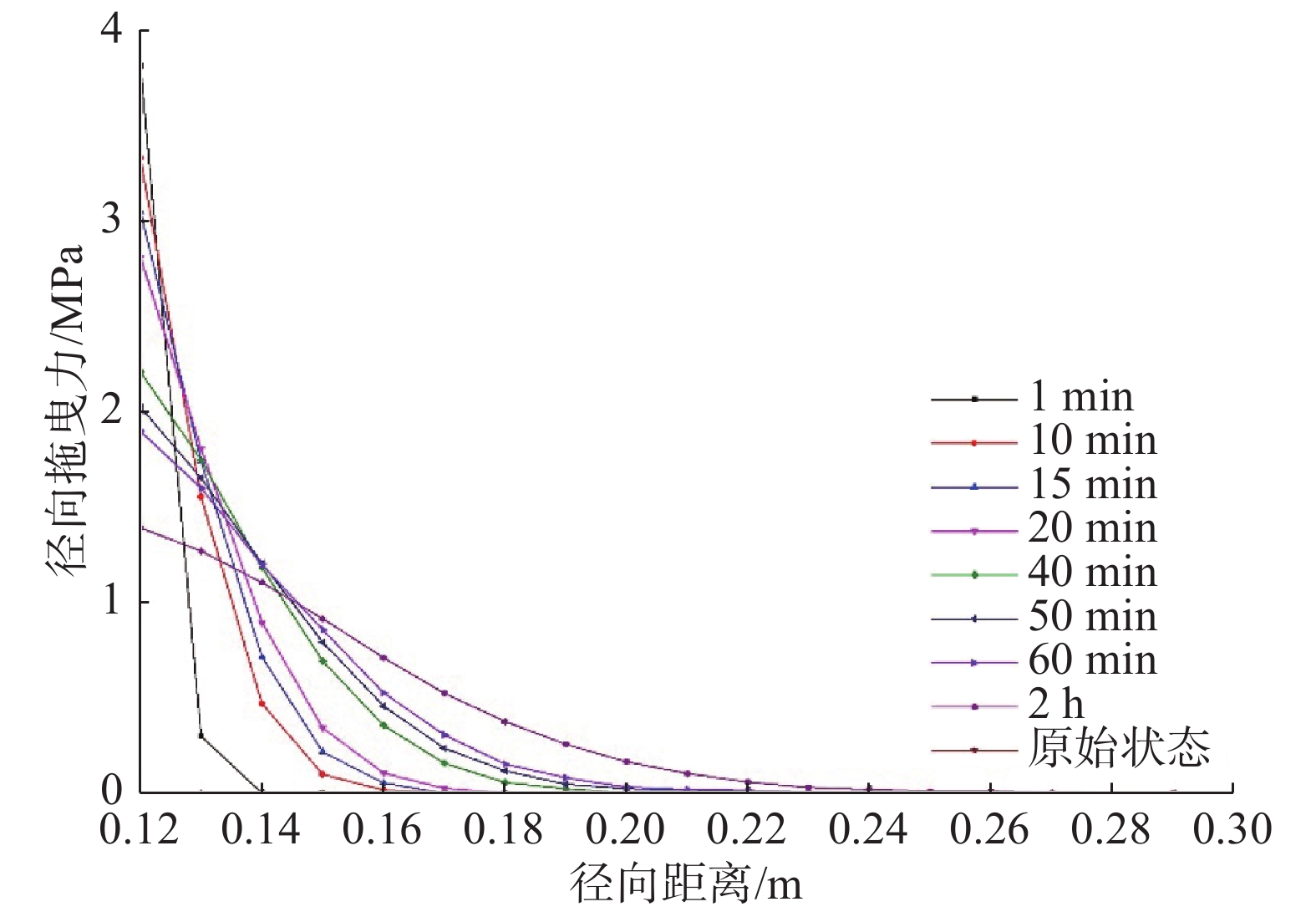
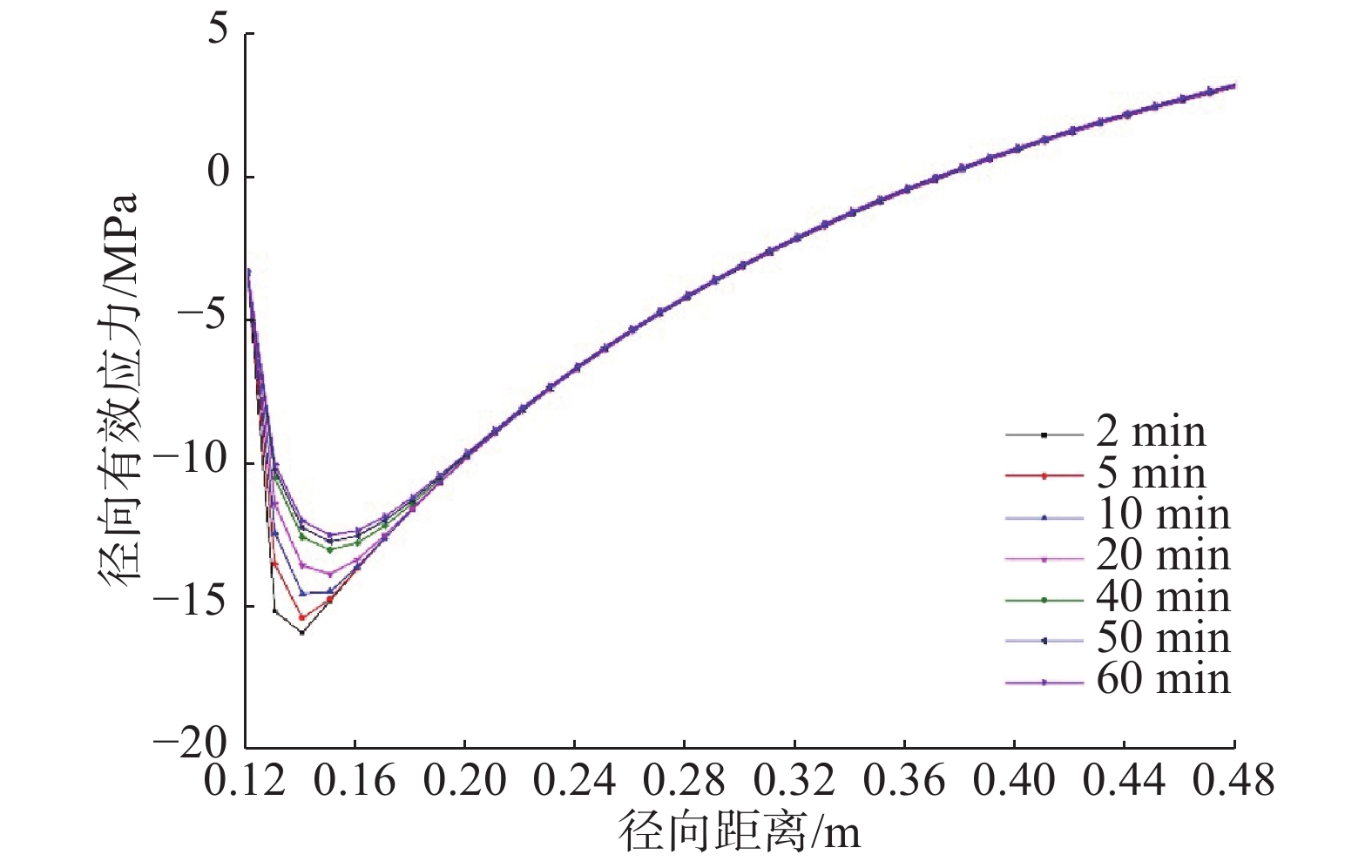
川西低渗透气藏采用气体钻井技术钻进时,致密砂岩井段井下垮塌频繁,为给制定防塌技术措施提供依据,在分析非达西渗流、储层敏感性对孔隙压力影响,计算气层产气时径向拖曳力的基础上,分析了径向拖曳力影响下井周的有效应力场,利用川西X3井实钻数据分析了气体钻井井壁垮塌的机理,并与摩尔库伦准则和拉伸破坏模型相结合,提出了适用于川西低渗透气藏气体钻井的井壁稳定性评价方法。川西低渗透气藏气体钻井井壁垮塌机理为:低渗透储层中高速非达西渗流和气体产出时产生的径向拖曳力使坍塌压力升高,井壁稳定性变差,同时在径向拖曳力作用下先发生拉伸破坏,随后地层压力降低进而发生剪切破坏,出现垮塌。利用低渗透气藏气体钻井井壁稳定性评价方法评价了X3井低渗透储层的井壁稳定性,评价结果与实钻情况相符,说明采用该评价方法可以评价川西低渗透气藏气体钻井时的井壁稳定性,能够为川西低渗透气藏气体钻井制定防塌技术措施提供指导。
Abstract:In gas drilling through low permeability gas reservoirs in Western Sichuan, borehole collapse occurs frequently in the tight sandstone sections. To develop a protocol for anti-collapse technical measures during gas drilling of such as in the kinds of gas reservoirs found in western Sichuan, effective stress around the wellbore under the influence of radial drag force has been analyzed based on the analysis of non-Darcy seepage and reservoir sensitivity on pore pressure, and radial drag force during gas production. The wellbore collapse mechanism of gas drilling was analyzed by using practical drilling data of Well X3 in Western Sichuan. Then a wellbore stability evaluation method during gas drilling through low permeability gas reservoirs in western Sichuan was proposed in combination with Mohr-Coulomb criterion and tensile failure model. Results showed that the high-speed non-Darcy seepage and the radial drag force generated during gas production in low permeability reservoir will increase the borehole collapse pressure, so damage borehole stability. Tensile failure occurs first under radial drag force, and then shear failure happens due to the decrease of formation pressure. Those rock failures result in wellbore collapse. Wellbore stability of Well X3 in the low permeability reservoir was evaluated using this method, and the results were consistent with the practical drilling situations. It demonstrated that this method could be used to evaluate wellbore stability during gas drilling in low permeability gas reservoir in western Sichuan, and it would provide a protocol and recommended best practices for the development of anti-collapse measures during gas drilling in low permeability gas reservoir in Western Sichuan.
-
Keywords:
- low permeability pool /
- gas drilling /
- hole stabilization /
- pore pressure /
- effective stress /
- Western Sichuan
-
致密砂岩储层属于非常规油气储集层[1–3],沉积过程中受到多种沉积作用的影响,储层非均质性强,孔隙结构复杂,孔喉微小,在同一孔隙度下储层的渗透率相差1~4个数量级,渗透率测井解释与准确预测是一项具有挑战性的研究工作[4–6]。
目前,储层渗透率计算方法主要有统计学方法和机器学习方法。统计学方法为基于岩心实验数据的经验统计模型和半经验半物理模型,常用模型包括指数模型、幂律模型[7]、Kozeny-Carman模型[8–9]、Timur模型[10]和SDR模型[11]等,但统计学方法得到的渗透率结果通常与实际测试存在偏差,且无法充分描述致密砂岩储层渗流规律与复杂孔喉结构之间的关系[12–13]。渗透率预测也可以采用机器学习方法,目前性能较好的机器学习模型主要有支持向量机[14]、随机森林 [15–16]和XGBoost[17]等。但是,浅层机器学习的结构单一,组合之后更是将各自的缺点叠加,如泛化能力受到制约,在渗透率预测中具有局限性。引入复杂的机器学习模型,如卷积神经网络[18]、循环神经网络[19]等,可以适应复杂的储集特征、地质沉积特征,以建立渗透率与测井数据间复杂的非线性映射关系。致密砂岩储层非均质性强,孔隙结构复杂,仅依靠机器学习模型直接预测渗透率难以取得较好的效果,对储层分类评价是描述储集层非均质性和渗流特征的有效途径。引入流动单元,将储层划分多类具有不同渗流特性的流动单元,采用流动单元指数作为流动单元划分的指标,建立多类流动单元下的渗透率测井解释模型,以提高渗透率评价精度 [20–25]。常用的流动单元指数预测方法包括多元回归法[26]、Fisher判别法[26]和机器学习法[27]。对于致密砂岩储层,流动单元指数与测井响应的线性相关性一般情况下较差,多元回归方法的拟合精度较低,Fisher法作为人工智能的初级阶段方法,其预测精度也远达不到要求。然而,当前的流动单元分类标准并不明确,因此,需要建立流动单元分类标准及其分类优选方法,以准确描述储层渗流特征和计算渗透率。
为此,笔者提出了流动单元分类标准和流动单元分类优选方法,并针对不同流动单元分类建立了渗透率解释模型,引入深度学习预测流动单元指数,为致密砂岩储层渗透率计算提供了模型基础。
1. 渗透率计算方法
1.1 流动单元分类与渗透率模型构建
1.1.1 流动单元分类指标
水力流动单元是将岩石矿物地质特征、孔喉特征结合起来综合判定孔隙几何特征参数,可较好地描述储集层储集特征、渗流特征和非均质特征。具有相似流动单元指数的岩石被认为具有相似的平均水力半径和流体流动特性,可归为同一类流动单元。从微观角度进行流动单元分类时,主要依据储层微观孔隙结构及物性特征,常根据 Kozeny-Carman(K-C)方程推导得到流动单元指数,划分储层流动单元。在K-C方程基础上引入平均水力半径和迂曲系数,得到修正K-C方程[8–9,28–29],数学表达式为:
K=ϕ3e(1−ϕe)21Fsτ2S2gv (1) 式中:K为渗透率,mD;
ϕe 为有效孔隙度;Fs 为孔隙形状系数;τ为孔隙介质的迂回度;Sgv 为颗粒体的表面积,cm2。流动单元可用流动单元指数来描述和量化:
IFZ=IRQϕz (2) 其中ϕz=ϕe1−ϕe (3) IRQ=0.01π√Kϕe=0.01π√FsτSgvϕe1−ϕe (4) 式中:IFZ为流动单元指数,μm;ϕz为标准化孔隙度指数;IRQ为储层品质因子。
迂回度τ描述了流体在孔隙介质中流动路径的曲折程度,较高的迂回度会导致流体在孔隙介质中的流动路径更长,流动阻力增大,导致流动单元指数值较低,储层流动效率较低。孔隙形状系数描述了孔隙的几何形状,不规则或非圆形孔隙会导致更高的局部流动阻力和更复杂的流动行为,也会导致流动单元指数值较低。孔隙形状与迂回度共同作用,进一步改变了流体流动路径,增大了流动阻力,进而改变了流动单元指数,影响渗流能力。
式(2)两边取对数,得:
lgIRQ=lgϕe+lgIFZ (5) 由式(5)可知,在
IRQ−ϕe 双对数坐标图上,所有具有相似流动单元指数值的岩心都应形成一条斜率为1.0的直线,因存在统计误差,斜率应在1.0左右变化。分析认为,位于同一直线的岩心具有相同的孔喉性质,属于同一类流动单元;不同流动单元指数值的岩心点将形成互相平行的直线,分属不同流动单元。根据流动单元指数,划分珠江口盆地惠州凹陷古近系恩平组致密砂岩储层流动单元(见图1)。1.1.2 流动单元分类标准及渗透率模型
建立流动单元划分标准时,可以通过
IRQ−ϕe 交会图、采用同类流动单元斜率为1.0的方式进行人为分类,但这种方法误差较大。为此,在IRQ−ϕe 交会图基础上,利用流动单元指数频数分布直方图及概率累计曲线图确定划分标准。首先,基于统计学原理,如果对同一事物在相同条件下进行多次测量或试验,观测结果通常会趋向于服从正态分布。对于同种流动单元内样品的测量相当于对该流动单元内单一样品的多次测量的结果,那么该样品某一物理量(如流动单元指数)在线性坐标下的形态为正态分布曲线,因此可以绘制流动单元指数频数分布直方图来观察流动单元指数正态分布特征,每类流动单元的流动单元指数应服从正态分布(见图2(a)的蓝色线),即同一沉积地质环境下的流动单元指数服从正态分布。从图2可以看出,该层存在多个非均质流动单元,流动单元指数分布特征一般由几个正态分布组成。然而,仅通过流动单元指数频数直方图分析流动单元正态分布特征较为困难,需要有效区分流动单元正态特征数量。引入概率累计曲线分析方法,作出的流动单元指数频率累计曲线,坐标是概率分度的百分数值,横坐标是(等差的)算术分度的流动单元指数对数值,通常是由若干直线段组成(见图2(b))。不同性质沉积相流动单元对应的流动单元指数,其线段的数目交切点和线段的斜率等性质亦不同,可直观地比较流动单元之间的差别。同一流动单元具有正态分布特征的流动单元指数累计概率形态在概率累计图中近似为一条直线,可以更直观地区分流动单元类型。流动单元分类后,对每类流动单元进行孔隙度–渗透率回归分析,建立每类流动单元的渗透率解释模型:Ki=aiebiϕe(i=1,2,⋯,n) (6) 式中:a和b为拟合系数;i为流动单元分类数目。
1.1.3 流动单元分类数目优选
确定流动单元分类标准后,需要进行流动单元类型数目优选,以提高渗透率计算精度。这是因为智能预测的流动单元指数本身带有一定的误差,其误差会传递到渗透率计算中,若需最小化计算渗透率误差,不仅要求流动单元分类数目合理,确保流动单元类型具有正态分布特征;而且通过岩心实验流动单元指数划分的流动单元类型还需要被测井数据感应识别出来,若流动单元分类数目太多,会导致无法进行测井识别和区分。
1.2 基于深度神经网络的流动单元指数预测
深度神经网络(DNN)具有较强的泛化能力,能够适应复杂地质条件和地区数据,能够处理流动单元指数与多种测井数据之间复杂的非线性关系,更好地分析测井数据中的隐藏模式,提高流动单元指数预测精度。研究使用的深度神经网络为深度全连接神经网络,由输入层、隐含层(多层)、输出层组成,且隐含层多于2层(见图3(a))。网络层与层之间是全连接的,即第i层的任意一个神经元与第i+1层的任意一个神经元相连(见图3(b))。
假设第i层具有m个神经元,第i+1层具有d个神经元,第i+1层中每个神经元包含一个偏置量,从第i层到第i+1层的关系为:
oi+1j=σ[m∑k=1(wi+1kxi+1k)+bi+1j](k=1, 2, …, m) (7) 式中:
o 是第i+1层的输出;w 是第i层到第i+1层的隐含层权重;x 是第i层的输出;b 是第i+1层偏置;k为神经元个数。可将式(7)写成矩阵形式:
\boldsymbol{o}=\sigma(\boldsymbol{W}\boldsymbol{X}+\boldsymbol{b}) (8) 式中:o为输出矩阵;W为权重矩阵;b为偏置矩阵。
多层网络结构可以继续堆叠隐藏层,层层堆叠,从而产生更强表达能力的模型[30]。选择不同层数、神经元个数和其他参数的组合模型,对比模型的训练效果和泛化能力,选择了6个隐含层,神经元数量为128×256×512×256×64×32。逐层增加神经元数(从128增至512),可以帮助网络在前期提取更多的高维特征;随后逐层减少神经元数(从512个减少至32个),可以帮助网络在后期逐渐归纳和总结特征,提升预测的精度和泛化能力。
选择ReLU作为激活函数,能够缓解梯度消失问题,并采用Adam优化器进行DNN模型训练,结合动量和自适应学习率的优点,能够在训练过程中快速收敛并减少局部最优的影响。利用交叉熵损失函数,通过反向传播算法自适应地调节学习速率,实现参数更新。深度神经网络通过多层结构、权重调整和激活函数,建立输入–目标的最优化非线性关系,提高任务学习和预测效率,表现出比浅层网络更强大的表达能力和泛化能力[30]。
1.3 渗透率计算流程
渗透率计算主要包括以下流程:1)根据岩心孔隙度和渗透率实验计算流动单元指数值,通过流动单元指数正态分布特征描述、最小化误差传递和流动单元测井识别,优选最优流动单元分类,并构建分类流动单元的渗透率解释模型;将流动单元指数与测井数据进行相关性分析,优选流动单元指数敏感测井数据;2)利用敏感测井数据建立DNN样本集,训练样本得到DNN模型,再通过该模型预测得到储层全井段的流动单元指数值;3)建立孔隙度模型,计算得到孔隙测井解释结果;4) 根据储层流动单元指数的预测结果,每个深度点选择对应的渗透率解释模型,再通过孔隙度解释结果求取储层全井段的渗透率(见图4)。
2. 实例应用分析
珠江口盆地惠州凹陷古近系恩平组属于典型的强非均质性特低渗致密砂岩储层,沉积相以扇三角洲和辫状河三角洲平原控制,具有临近物源区、构造作用强、地形坡度大和沉积作用强等沉积背景。恩平组整体表现为厚砂薄泥,岩性以中砂岩和砂砾岩为主,具有近源、分选差和磨圆差的特征。砂岩以岩屑长石砂岩和长石岩屑砂岩为主,矿物类型以石英为主,黏土含量在10%左右,黏土矿物类型主要为伊利石;岩心分析孔隙度为3%~16%,渗透率为0.01~100.00 mD,孔隙度与渗透率相关性差,孔隙度相近岩心的渗透率差异较大,非均质性和各向异性较强,测井响应特征难以表征储层的真实孔隙性和流体特性;测井解释具有模糊和不确定性,常规渗透率解释模型已无法准确计算储层渗透率。
2.1 流动单元指数预测
测井参数和流动单元指数之间具有一定的相关性,通过相关性分析选取敏感的测井参数作为深度神经网络输入数据。通过流动单元指数敏感性分析可知,流动单元指数较敏感测井参数为孔隙度和浅电阻率,较敏感参数为补偿密度和T2几何均值,较差敏感参数为补偿中子和自然伽马(见图5)。
深层致密油气层的流动单元指数与大多数测井参数的线性相关性较差,因此考虑将与流动单元指数线性关系较差的测井参数加入智能预测中,以提高流动单元指数预测精度。渗透率计算误差为:
e=\left|\mathrm{lg}K_{\text{pre}}-\mathrm{lg}K_{\mathrm{lab}}\right| (9) 式中:e为渗透率对数绝对误差;
{K_{{\text{pre}}}} 为智能预测的渗透率,mD;K_{\mathrm{lab}} 为岩心实验渗透率,mD。输入参数包含(较)敏感参数补偿密度、孔隙度、T2几何均值和浅电阻率时,误差为0.29;输入参数增加补偿中子时,误差为0.22;输入参数再加入自然伽马时,误差为0.17(见图6),可以看出加入线性相关性较差的测井参数后,流动单元指数预测精确度得到提高,因此,后续将(较)敏感及不敏感的测井参数都作为输入层数据。最终的输入测井参数包括自然伽马(岩性)、补偿密度(储集性)、补偿中子(储集性) 、浅电阻率(传导性) 、孔隙度(储集性),T2几何均值(储集性和传导性)。
2.2 流动单元分类数目优选及渗透率模型构建
将流动单元分别分为3类、4类、5类和6类流动单元(见图7),并建立不同流动单元分类数目的渗透率解释模型(见图8)。
流动单元不同分类数目的渗透率计算结果如图9所示。其中,分为3类误差为0.72,4类误差为0.57,5类误差为0.51,6类误差为0.54。分为5类误差最小,因此优选5类为最佳流动单元分类,并建立渗透率测井解释模型,实际应用时可以确定测井响应是否能有效区分5类流动单元类型。5类流动单元的沉积相、岩性及物性见表1。
5类渗透率测井解释模型可以表示为:
K=\left\{\begin{array}{*{20}{l}}0.002\ 5\mathrm{e}^{0.289\phi},\begin{array}{*{20}{c}} & I_{\text{FZ}}\leqslant0.45\end{array} \\ 0.014\ 8\mathrm{e}^{0.402\phi},\begin{array}{*{20}{c}} & 0.45 < I_{\text{FZ}}\leqslant1.42\end{array} \\ 0.118\ 0\mathrm{e}^{0.371\phi},\begin{array}{*{20}{c}} & 1.42 < I_{\text{FZ}}\leqslant3.00\end{array} \\ 0.556\ 4\mathrm{e}^{0.389\phi},\begin{array}{*{20}{c}} & 3.00 < I_{\text{FZ}}\leqslant8.00\end{array} \\ 3.269\ 8\mathrm{e}^{0.362\phi},\begin{array}{*{20}{c}} & I_{\text{FZ}} > 8.00\end{array}\end{array}\right. (10) 式中:ϕ为孔隙度。
表 1 5类流动单元类型的储层特征Table 1. Reservoir properties of flow units with five types流动单元分类 沉积微相 流动单元指数/μm 岩性 孔隙度,% 渗透率/mD Ⅰ类 分流间湾 IFZ≤0.45 泥质粉砂岩、中–细砂岩为主 5.4~15.0(9.4) 0.01~0.96(0.08) Ⅱ类 河口坝 0.45 < IFZ≤1.42 中–细砂,少量粗砂和含砾中砂 5.0~16.1(9.8) 0.07~11.00 (0.75) Ⅲ类 河口坝, 分流河道 1.42< IFZ≤3.00 中–细砂为主,含砾粗砂次之 6.2~16.2(10.7) 0.56~48.00 (6.76) Ⅳ类 分流河道 3.00< IFZ≤8.00 中–粗砂为主,含砾粗砂次之 7.0~15.2(12.1) 2.9~379.0(70.0) Ⅴ类 分流河道 IFZ >8.00 粗砂和含砾粗砂 9.0~17.6(14.2) 101~ 3611 (758)注:孔隙度及渗透率数值后()内数值为平均值。 2.3 解释及分析
HZ–26–A井恩平组早期发育内前缘河道砂砾岩沉积、中期内前缘分流河道砂砾岩沉积、晚期前缘河口坝中砂岩沉积(见图10)。采用基于DNN的流动单元指数预测方法和优选的5类流动单元渗透率解释模型进行计算分析。
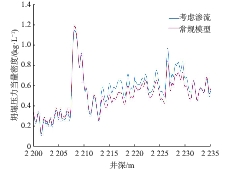
测井孔隙度(孔隙度道)由密度孔隙度解释模型计算得到,流动单元指数道由DNN预测得到,预测流动单元指数与岩心分析流动单元指数匹配较好。通过储层流动单元指数再将储层进行渗流特性分级,分为5类流动单元(流动单元道1~5),数值越高,代表渗流特性越好。该井恩平组上段沉积相以河口坝为主,分流河道次之;下段沉积微相主体为水下分流河道,夹杂少量分流间湾。分流间湾自然伽马值高,主要由灰绿色泥岩、粉砂岩组成,平均孔隙半径小于0.5 μm,渗流能力差,对应Ⅰ类流动单元;河口坝自然伽马曲线呈漏斗–箱型,齿化明显,以Ⅱ类或Ⅲ类流动单元类型为主,平均孔隙半径大于0.5 μm,渗透率在0.2~3.0 mD。水下分流河道自然伽马曲线呈齿化箱型,岩性变化较大,说明岩性无法区分沉积环境,也无法区分流动单元类型,该微相可跨多个粒度区间,在概率累计曲线常表现为典型的“三段式”,对应的流动单元类型也表现为三段式,以Ⅲ类至Ⅴ类流动单元类型为主,平均孔隙半径大于1.0 μm,渗透率大于1.0 mD;从渗透率综合解释结果可知,渗流单元分级明显,流动单元类型与沉积相也具有较好的相关性,说明能够根据测井数据区分流动单元类型。不同深度点根据流动单元指数值选择不同渗透率解释模型,再利用储层孔隙度计算得到储层渗透率(渗透率道)。实例计算结果可知,基于智能预测和流动单元优选分类法计算的渗透率优于核磁SDR模型计算的渗透率,与岩心渗透率匹配更好。
流动单元分类和优选方法可以拓展到大多数低渗碎屑岩、火山岩等储层,但对于极为复杂的储层环境,如复杂的孔–缝–洞储集体,该方法具有一定局限性,简单的孔隙度和渗透率关系不能表达复杂孔隙结构的流动特性,可结合较为先进的测井技术进行联合分析,如电成像和声波远探测技术可以刻画多尺度孔缝特征,数字岩石物理技术可以描述微观孔隙结构和揭示渗透率微观响应机理,多种测井技术联合是未来测井解释评价的发展方向。
3. 结论与建议
1)利用流动单元在流动单元指数频数分布直方图和概率累计图的正态特征,建立了流动单元分类标准。基于最小化误差传递,提出了流动单元类型优选方案,建立了能适应复杂地质条件的多类渗透率模型。
2)通过测井序列与流动单元指数的相关性分析,建立了流动单元指数敏感测井序列,引入深度神经网络准确预测了全井段的流动单元指数,可为储层流动单元划分提供分类指标。
3)基于流动单元分类标准及优选方法,确定恩平组流动单元最佳分类数量为5类,5类流动单元类型与沉积相具有较好的相关性,能明显提高储层渗透率的计算精度。
4)流动单元分类和优选方法依赖高质量的测井和岩心数据,在数据不足的情况下,分类结果会存在误差。对于极为复杂的储层环境,如孔−缝−洞储集体,该方法具有一定局限性,建议结合电成像、声波远探测、数字岩石物理等测井技术进行分类,以提高储层品质评价精度。
-
-
[1] 蒋祖军, 张杰, 孟英峰, 等. 气体钻井井壁稳定性评价方法分析[J]. 天然气工业, 2007, 27(11): 68–70 doi: 10.3321/j.issn:1000-0976.2007.11.020 JIANG Zujun, ZHANG Jie, MENG Yingfeng, et al. Analysis on the methods used to evaluate the wellbore stability of gas drilling[J]. Natural Gas Industry, 2007, 27(11): 68–70 doi: 10.3321/j.issn:1000-0976.2007.11.020
[2] 李皋, 孟英峰, 刘厚彬, 等. 气体快速钻井井壁失稳研究[J]. 钻采工艺, 2013, 36(4): 26–30 doi: 10.3969/J.ISSN.1006-768X.2013.04.08 LI Gao, MENG Yingfeng, LIU Houbin, et al. Evaluation methods of borehole instability in gas drilling[J]. Drilling & Production Technology, 2013, 36(4): 26–30 doi: 10.3969/J.ISSN.1006-768X.2013.04.08
[3] 刘厚彬, 孟英峰, 万尚贤, 等. 高压气层气体钻井井壁稳定性分析[J]. 天然气工业, 2010, 30(11): 59–62 doi: 10.3787/j.issn.10000976.2010.11.016 LIU Houbin, MENG Yingfeng, WAN Shangxian, et al. Analysis of wellbore stability during gas drilling through high-pressure gas formations[J]. Natural Gas Industry, 2010, 30(11): 59–62 doi: 10.3787/j.issn.10000976.2010.11.016
[4] 邹灵战, 邓金根, 曾义金, 等. 气体钻井钻前水层预测与井壁稳定性研究[J]. 石油钻探技术, 2008, 36(3): 46–49 doi: 10.3969/j.issn.1001-0890.2008.03.011 ZOU Lingzhan, DENG Jingen, ZENG Yijin, et al. Study of formation water production prediction and wellbore stability in gas drilling[J]. Petroleum Drilling Techniques, 2008, 36(3): 46–49 doi: 10.3969/j.issn.1001-0890.2008.03.011
[5] 金衍, 陈勉, 卢运虎, 等. 一种气体钻井井壁稳定性分析的简易方法[J]. 石油钻采工艺, 2009, 31(6): 48–52 doi: 10.3969/j.issn.1000-7393.2009.06.012 JIN Yan, CHEN Mian, LU Yunhu, et al. A simple means for gas drilling wellbore stability analysis[J]. Oil Drilling & Production Technology, 2009, 31(6): 48–52 doi: 10.3969/j.issn.1000-7393.2009.06.012
[6] 刘新福, 綦耀光, 胡爱梅, 等. 单相水流动煤层气井流入动态分析[J]. 岩石力学与工程学报, 2011, 30(5): 960–966 http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb201105012 LIU Xinfu, QI Yaoguang, HU Aimei, et al. Inflow performance analysis of single-phase water flow in coalbed methane wells[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(5): 960–966 http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb201105012
[7] 杨朝蓬, 高树生, 刘广道, 等. 致密砂岩气藏渗流机理研究现状及展望[J]. 科学技术与工程, 2012, 12(32): 8606–8613 doi: 10.3969/j.issn.1671-1815.2012.32.026 YANG Zhaopeng, GAO Shusheng, LIU Guangdao, et al. The research status and progress on percolation mechanism of tight gas resvervoir[J]. Science Technology and Engineering, 2012, 12(32): 8606–8613 doi: 10.3969/j.issn.1671-1815.2012.32.026
[8] 高树生, 熊伟, 刘先贵, 等. 低渗透砂岩气藏气体渗流机理实验研究现状及新认识[J]. 天然气工业, 2010, 30(1): 52–141 doi: 10.3787/j.issn.1000-0976.2010.01.014 GAO Shusheng, XIONG Wei, LIU Xiangui, et al. Experimental research status and several novel understanding on gas percolation mechanism in low-permeability sandstone gas reservoirs[J]. Natural Gas Industry, 2010, 30(1): 52–141 doi: 10.3787/j.issn.1000-0976.2010.01.014
[9] 郭世慧. 一种气体非线性渗流理论及其应用[D]. 北京: 中国地质大学(北京), 2009. GUO Shihui. The theory and application of a kind of gas nonlinear seepage[D]. Beijing: China University of Geosciences (Beijing), 2009.
[10] 王晓琴, 吴聚, 冉艳, 等. 非线性渗流对异常高压气藏产能的影响[J]. 岩性油气藏, 2012, 24(4): 125–128 doi: 10.3969/j.issn.1673-8926.2012.04.025 WANG Xiaoqin, WU Ju, RAN Yan, et al. Influence of non-liner flow on productivity of abnormal high pressure gas reservoir[J]. Lithologic Reservoirs, 2012, 24(4): 125–128 doi: 10.3969/j.issn.1673-8926.2012.04.025
[11] 雷征东, 李相方, 程时清. 考虑拖曳力的出砂预测新模型及应用[J]. 石油钻采工艺, 2006, 28(1): 69–72, 86 doi: 10.3969/j.issn.1000-7393.2006.01.019 LEI Zhengdong, LI Xiangfang, CHENG Shiqing. Modeling and application to sand prediction considering of drag force[J]. Oil Drilling & Production Technology, 2006, 28(1): 69–72, 86 doi: 10.3969/j.issn.1000-7393.2006.01.019
[12] 邓金根. 井壁稳定预测技术[M]. 北京: 石油工业出版社, 2008. DENG Jingen. The predicting technique of wellbore stability[M]. Beijing: Petroleum Industry Press, 2008.
[13] ZHANG Jincai, STANDIFIRD W B, ADESINA K, et al. Wellbore stability with consideration of pore pressure and drilling fluid interactions[R]. ARMA/USRMS 06-922, 2006.
[14] CUI L, EKBOTE S, ABOUSLEIMAN Y. Effect of pore fluid conditions at the borehole wall on borehole stability[R]. ARMA-99-0187, 1999.













 下载:
下载: