可溶桥塞整体式卡瓦结构优化设计

郝地龙; 何霞; 王国荣; 方兴; 廖代胜; 方海辉

doi:10.11911/syztjs.2018151

可溶桥塞整体式卡瓦结构优化设计

郝地龙^{1, 2,},
何霞^{1, 2},
王国荣^{1, 2, 3},
方兴^{1, 2},
廖代胜^{1, 2},
方海辉^{1, 2}

1.
西南石油大学机电工程学院，四川成都 610500
2.
西南石油大学能源装备研究院，四川成都 610500
3.
油气藏地质及开发工程国家重点实验室(西南石油大学)，四川成都 610500

基金项目:

四川省青年基金项目“极端工况下压缩式封隔器胶筒-化学-力多场耦合行为及密封机理研究” 2017JQ0029

详细信息

作者简介:
郝地龙(1993—)，男，云南曲靖人，2017年毕业于长春大学机械工程专业，在读硕士研究生，主要从事封隔器设计方面的研究工作。E-mail:2608083214@qq.com

中图分类号: TE925⁺.2
计量
- 文章访问数: 10024
- HTML全文浏览量: 5491
- PDF下载量: 101
出版历程
- 收稿日期: 2018-06-20
- 修回日期: 2018-09-27
- 网络出版日期: 2022-09-08
- 刊出日期: 2018-12-31

Optimization of the Structural Design of the Integral Slip of a Soluble Bridge Plug

HAO Dilong^{1, 2,},
HE Xia^{1, 2},
WANG Guorong^{1, 2, 3},
FANG Xing^{1, 2},
LIAO Daisheng^{1, 2},
FANG Haihui^{1, 2}

1.
College of Mechanical and Electrical Engineering, Southwest Petroleum University, Chengdu, Sichuan, 610500, China
2.
Research Institute of Energy and Equipment, Southwest Petroleum University, Chengdu, Sichuan, 610500, China
3.
State Key Laboratory of Oil and Gas Reservoir Geology and Development, Southwest Petroleum University, Chengdu, Sichuan, 610500, China

摘要

摘要:
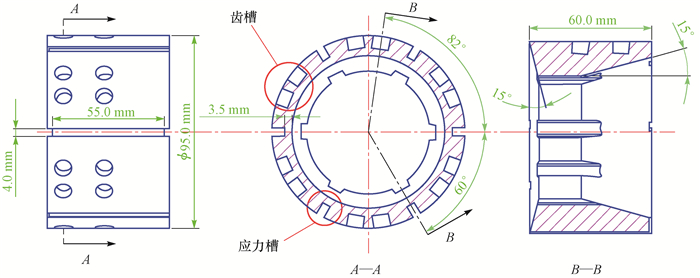
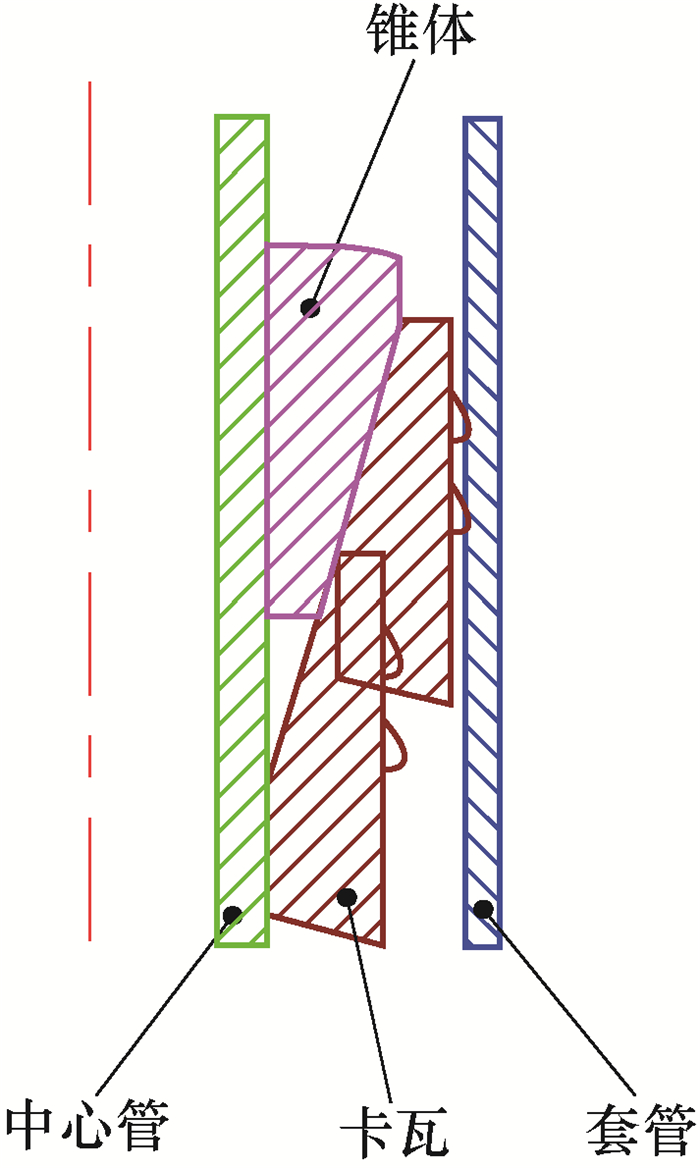
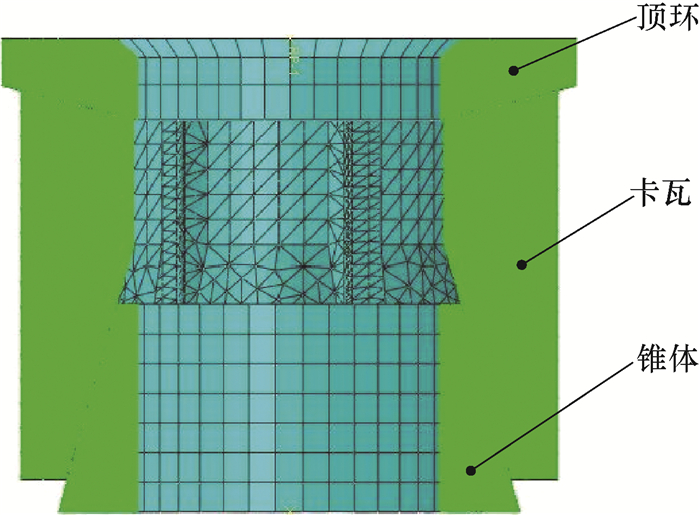
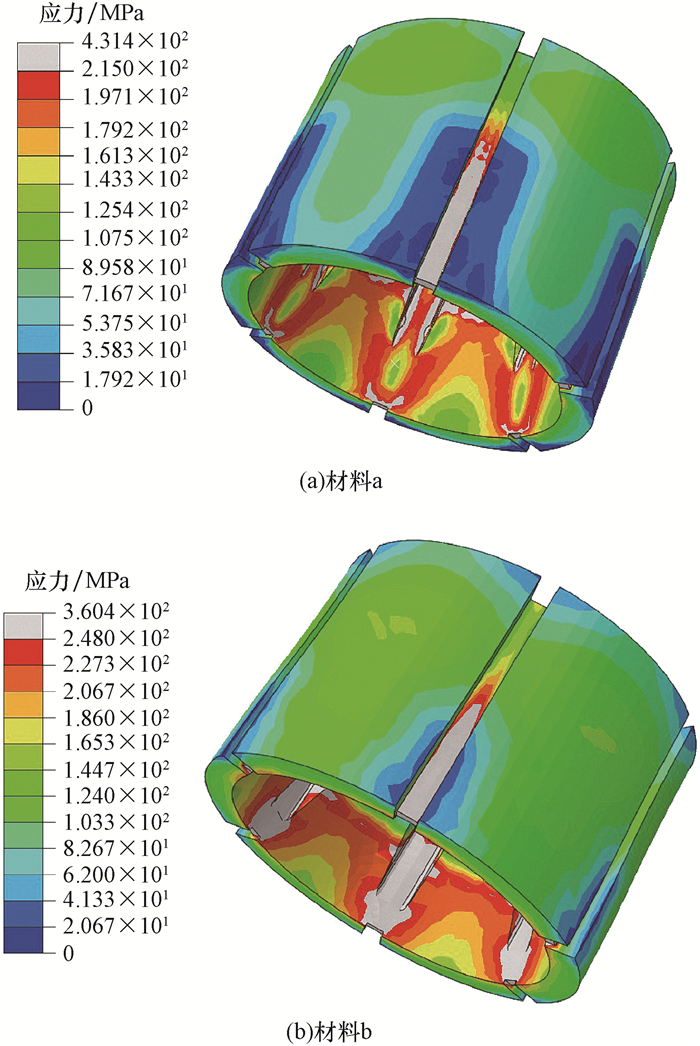
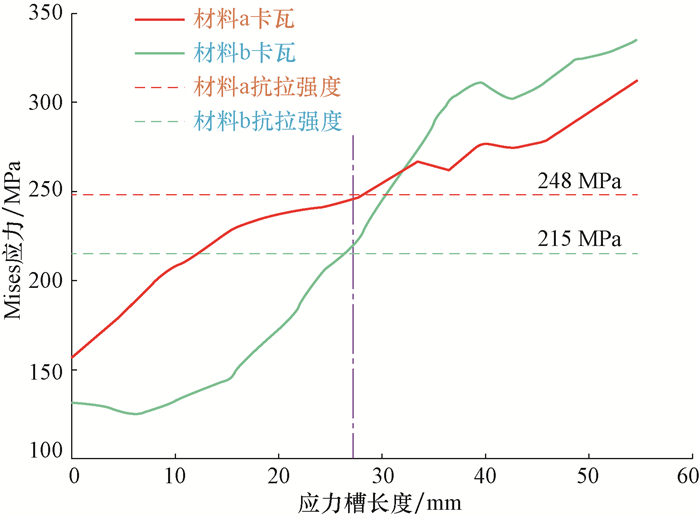
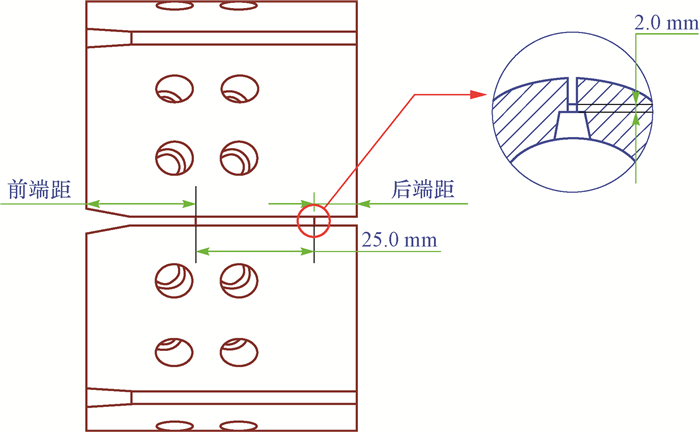
为提高可溶桥塞整体式卡瓦的锚定效果，以适用于ϕ95.0 mm可溶桥塞的整体式卡瓦为例，对其结构进行了优化设计。通过整体式卡瓦断裂试验和断裂数值模拟发现，在轴向载荷作用下，整体式卡瓦应力槽在其长度1/2处所受应力达到抗拉强度时，卡瓦断裂张开。基于此规律，通过数值模拟将整体式卡瓦的结构优化为采用6个均匀分布的应力槽，应力槽长25.0 mm、厚2.0 mm、宽4.0 mm，距前端25.0 mm、后端10.0 mm。结构优化后卡瓦的断裂力为72 kN，达到了ϕ95.0 mm可溶桥塞坐封时卡瓦断裂力的要求，且数值模拟及断裂试验均表明，结构优化后的整体式卡瓦不再呈C字形张开，其承压能力更强，卡瓦的锚定效果更好。研究结果表明，可溶桥塞整体式卡瓦的结构经优化设计后，其断裂力明显降低，能避免呈C字形张开，其锚定效果得到增强。
- 可溶桥塞 /
- 整体式卡瓦 /
- 结构设计 /
- 数值模拟
Abstract:
In order to improve the anchoring performance of the integral slip of a soluble bridge plug, the team took the design of the integral slip suitable for a ϕ95.0 mm soluble bridge plug as an example, and then proposed a structural optimization design.According to the results from fracture experiments and numerical simulation of the integral slip, when the groove length 1/2 and above reach tensile strength under the effect of axial force, the slip fracture opens.Based on this law, the structure of stress groove was optimized by a numerical simulation.The integral slip adopted the form of six stress grooves, the length, thickness and width of stress groove were 25.0 mm, 2.0 mm and 4.0 mm, respectively.The distance from the front end and back end was 25.0 mm and 10.0 mm, respectively.Under this structure, the breaking force of the slip was 72 kN, which met the technical requirements of the slip breaking force when the ϕ95.0 mm soluble bridge plug was sealed.Moreover, numerical simulations and fracture experiments both showed that the integral slip after structural optimization could avoid C-shaped openings, resulting in better pressure bearing capacity and better anchoring performance of the slip.The results also demonstrated that, after structural optimization design, the breaking force of the integral slip of soluble bridge plug experienced an obvious decrease.The integral slip is capable of avoiding a C-shaped opening, which can improve the anchoring performance.
- soluble bridge plug /
- integral slip /
- structure design /
- numerical simulation

HTML全文

水平井、大位移井和分支井等复杂结构井钻井过程中，井场人员需要实时了解各种井下参数，如井斜角、方位角和工具面等^[1-3]。钻井液脉冲传输是钻井过程中应用最为广泛的数据传输方式，其基本原理是控制井下脉冲发生器按照一定编码规则工作，不断改变钻杆里钻井液的压力，以压力波脉冲的形式将测量数据传送至地面^[4-8]。然而，经过编码后的脉冲信号在钻井液中传播时不可避免地会受到井场电压、地面钻井泵、钻井液中气泡以及运动钻具等各种噪声源的干扰，必须经过去噪和识别处理才能得到井下真实的测量数据。针对脉冲位置调制（pulse position modulation，PPM）码钻井液脉冲信号，李艳军^[9]提出了一种基于低通滤波和方波相关的信号去噪方法，段友祥等人^[10]提出了一种基于可信度分析的信号识别方法，胡永健等人^[11]提出了一种基于小波变换和自动阈值调节的信号处理方法，这些方法均取得了一定效果。然而，在深井、超深井和小井眼等复杂井眼环境下，编码脉冲信号的路径损耗和码间干扰明显增强，对钻井液脉冲信号处理提出了更高的要求^[12-15]。为了满足微弱PPM码钻井液脉冲信号处理要求，笔者提出了一种基于优化变分模态分解（variational mode decomposition，VMD）和互相关的钻井液脉冲信号处理方法，并利用现场资料与传统方法进行对比，验证了该方法在压制杂波、保留编码脉冲特征和抗异常干扰等方面的有效性。

1. 传统信号处理方法及其不足

PPM编码是一种常见的钻井液脉冲信号编码方式，其本质是以时间间隔为数据流传输信息^[4,9]。PPM码钻井液脉冲信号传统的处理方法主要包括带通滤波、阈值设定和峰值检测等^[2,9,11]。带通滤波算法可以用来对原始信号进行去噪，阈值设定算法可以用来去除杂波，峰值检测算法可以用来识别去噪后的信号。具体步骤是：1）对原始钻井液脉冲信号进行带通滤波处理，得到去噪后的信号；2）对去噪后的信号进行阈值设定，去除杂波；3）对去除杂波的信号进行峰值检测，得到各有效脉冲的位置；4）根据同步头中各脉冲的位置关系得到数据帧的起始位置；5）划分数据块，数据块中有效脉冲的位置所对应的十六进制数即为该数据块内波形所代表的码值；6）根据各测量参数的位数，将各数据块对应的码值进行组合，最终根据各测量参数的量程，将组合后的十六进制数转换成井下真实的测量结果。

钻井液脉冲信号是一种非平稳信号，传统的带通滤波、阈值设定等方法的参数设置依赖于人工选择，在复杂井眼环境下存在去噪效果较差和适应性不强等问题。

2. 改进的信号处理方法

变分模态分解是一种自适应、完全非递归的信号分解估计方法，通过迭代搜寻变分模型最优解来确定每个分量的频率中心和带宽，能够自适应地实现信号的频域剖分及各分量的有效分离。此外，由于钻井液脉冲信号中噪声信号与有效脉冲之间相的关性较弱，应用互相关法可以有效抑制干扰噪声。互相关法不考虑信号的频率，对未知频率的信号也可以进行处理，适合有效脉冲的检测。

基于上述思路，提出了一种基于优化变分模态分解和互相关的钻井液脉冲信号处理方法。该方法主要包括粒子群优化算法（particle swarm optimization, PSO）、VMD算法和互相关算法：PSO算法用来对VMD算法中的惩罚因子α和分解个数K进行寻优^[3,16-17]；VMD算法用来分解原始信号，去除干扰噪声^[16-18]；互相关算法用来识别去噪后的信号^[9,19-20]。具体处理步骤为：

1）初始化PSO各项参数，构造适度函数，设置惩罚因子α和分解个数K的寻优范围。通常，适度函数可以设置为原始信号和重构信号的均方根误差与原始信号和重构信号的互相关系数之比。评估每个粒子的适度函数值，判断各粒子是否满足种群进化停止条件，若不满足则继续寻优，直到满足最大种群进化预设值^[3,16-17]。

2）用获得的最优参数对钻井液脉冲原始信号进行VMD分解，得到本征模态分量。即：

$x\left( t \right) = \sum\limits_{k = 1}^K {{u_k}\left( t \right)}$

(1)

${u_k}\left( t \right) = {A_k}\left( t \right)\cos \left( {{\varphi _k}\left( t \right)} \right)$

(2)

式中：x(t)为原始信号；u_k(t)为第k个模态的信号；A_k(t)和 $\varphi _k(t)$ 为该模态的瞬时幅度和相位^[16-18]。

在较小的时间范围内，u_k(t)可以看作谐波信号，能量主要集中在频率f_k处。VMD同时计算所有模式波形及其中心频率，该过程可以看作寻找一组使变分约束问题最小化的u_k(t)和f_k。通过引入惩罚因子α和拉格朗日乘子λ，可使相应的变分约束问题转化为非约束变分问题，其增广拉格朗日函数定义为^[16-18]：

$\begin{gathered} L\left( {{u_k}\left( t \right),{f_k},\lambda \left( t \right)} \right) = a\sum\limits_{k = 1}^K {\left\| {\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\left( {\delta \left( t \right) + \frac{{\rm{j}}}{{{\text{π}} t}}} \right) * {u_k}\left( t \right)} \right]{{\rm{e}}^{ - {\rm{j}}2{\text{π}} {f_k}t}}} \right\|_2^2}+ \\ \left\| {x\left( t \right) - \sum\limits_{k = 1}^K {{u_k}\left( t \right)} } \right\|_2^2 + \left\langle {\lambda \left( t \right),x\left( t \right) - \sum\limits_{k = 1}^K {{u_k}\left( t \right)} } \right\rangle \\[-16pt] \end{gathered}$

(3)

式中：*代表卷积；假定2个函数分别为p(t)和q(t)，则<p(t), q(t)>表示内积，||p(t)|| $_2^2$ 表示2-范数。

对增广拉格朗日函数进行时频域转换后可以求取对应的极值解，从而得到模态分量和中心频率的表达式^[16-18]。对于第 n +1次迭代，满足：

$\hat u_k^{n + 1}\left( \omega \right) = \frac{{\hat x_k^{n + 1}\left( \omega \right) - \displaystyle\sum\limits_{i \ne K} {{{\hat u}_k}\left( \omega \right) + \dfrac{\hat \lambda \left( \omega \right)}{2}} }}{{1 + 2\alpha {{\left( {\omega - {\omega _k}} \right)}^2}}}$

(4)

$\,其中\qquad\qquad \omega _k^{n + 1} = \frac{{\displaystyle\int_0^\infty {\omega {{\left| {{{\hat u}_k}\left( \omega \right)} \right|}^2}{\rm{d}}\omega } }}{{\displaystyle\int_0^\infty {{{\left| {{{\hat u}_k}\left( \omega \right)} \right|}^2}{\rm{d}}\omega } }} \qquad\qquad$

(5)

式中，包含“^”上标的变量为不包含“^”上标变量的傅里叶变换。

通过不断迭代即可得到x(t)的K个模态分量。

3）根据各本征模态分量的频谱特征，将其依次分为随机噪声、泵冲信号、基线信号和有用信号，将有用信号模态分量叠加可以得到去噪后的信号。

4）构造同步头相关器，将去噪后的信号与同步头相关器进行互相关处理，相关后波形最大值所对应的位置即为数据帧的起始位置。基于同步头相关器进行起始位置确定时的互相关函数满足：

${r_{xy}}\left( \tau \right) = \sum\limits_{t = - \infty }^{ + \infty } {x\left( t \right)y\left( {t - \tau } \right)}$

(6)

式中：r_xy为相关值；x(t)为待相关信号；y(t)为同步头相关器。

需要注意的是，相关器中各点的平均值应为零，否则输出将随基线压力而变化。常用的相关器包括矩形相关器、三角形相关器和礼帽相关器等^[9,19-20]。

5）分别构造代表十六进制数0x0～0xF的数据块相关器，将去噪后的信号与各数据块相关器进行互相关处理，最大相关值所对应的十六进制数即为该数据块内波形所代表的码值。基于数据块相关器进行码值确定时的互相关函数满足：

${r_{xy}}\left( i \right) = \sum\limits_{t = - \infty }^{ + \infty } {x\left( t \right){y_i}\left( t \right)}$

(7)

6）根据各测量参数的位数，将各数据块对应的码值进行组合。最终根据各测量参数的量程，将组合后的十六进制数转换成井下真实的测量结果。

3. 传统方法与改进方法的对比分析

苏北地区某小井眼页岩油井现场采集的一段钻井液脉冲原始信号如图1所示。分析可知，由于受各种噪声的干扰，原始信号十分复杂，无法直接从中准确地分辨出编码脉冲，需要对钻井液脉冲原始信号进行去噪和识别处理，才能够得到真实的井下测量数据。分别采用传统和改进的信号处理方法对图1中的钻井液脉冲原始信号进行处理，以对比分析上述2种方法在去噪、同步头识别和码值判别等方面的应用效果。

图 1 钻井液脉冲原始信号

Figure 1. Original pulse signal of drilling fluid

下载: 全尺寸图片幻灯片

3.1 去噪效果

去噪是钻井液脉冲信号处理的关键步骤之一，直接决定信号识别的准确性。分别利用带通滤波算法和优化VMD算法处理钻井液脉冲原始信号，结果如图2和图3所示。对于优化VMD算法，为了加快计算速度，设置K的取值范围为[2,10]，α的取值范围为[100,5 000]，K的更新步长为1，α的更新步长为100。

图 2 经过带通滤波处理的钻井液脉冲信号（带通滤波器的通带频率0.1～0.4 Hz）

Figure 2. Pulse signal of drilling fluid after bandpass filtering (the passband frequency of the bandpass filter is 0.1 ～ 0.4 Hz)

下载: 全尺寸图片幻灯片

图 3 钻井液脉冲原始信号的变分模态分解结果（K=8，α=1 000）

Figure 3. VMD results of original pulse signal of drilling fluid (K=8，α=1 000)

下载: 全尺寸图片幻灯片

由图2可知，经过带通滤波处理后，钻井液脉冲原始信号中的噪声被明显压制，编码脉冲的形态得以展现出来。由图3可知，经过优化VMD算法处理后，钻井液脉冲原始信号中各种模态分离较为彻底。由于泵冲信号的频谱特征是在泵冲基频的整数倍处有明显的能量极大值，故可判断IMF6为泵冲基波，频率约为0.99 Hz；IMF4和IMF3分别为泵冲二次和三次谐波，频率分别约为1.98和2.97 Hz；IMF5、IMF2和IMF1为部分泵冲谐波和部分高频噪声的叠加；由于基线信号的频谱特征是能量主要集中在0.10 Hz以下的低频处且能量很强，故可判断IMF8为基线信号；由于随机噪声的频谱特征为全频率分布，故可判断残余分量为部分随机噪声和部分泵冲谐波的叠加；由于有用信号的能量主要集中在脉冲周期的倒数附近，故可判断IMF7为有用信号。

将带通滤波和优化VMD去噪后的信号进行对比，结果如图4所示。分析可知，尽管有用信号幅度仅为原始信号幅度的0.5%左右，但2种去噪方法均能有效地压制噪声，进而较为明显地从有用信号中分辨出编码脉冲。根据编码规则可以初步判断，15.3～26.3和162.3～173.2 s的3个连续脉冲可能为同步头信号，56.3～71.7，93.4～109和131.3～146.9 s的2个幅度较高的脉冲可能为数据信号，其他为杂波。对比35～53，73～91和112～128 s的杂波幅度可知，与带通滤波算法相比，优化VMD算法能够更好地压制杂波。

图 4 带通滤波和优化VMD去噪效果对比

Figure 4. Comparison of de-noising effects between bandpass filtering and optimal VMD

下载: 全尺寸图片幻灯片

3.2 同步头识别效果

寻找同步头是信号识别的第一步。寻找同步头的传统方式是检测去噪后信号的峰值，判断相邻波峰之间的时间间隔是否符合同步头特征。然而，由于去噪算法并不能完全去除所有干扰，去噪后的波形中必然存在诸多伪峰^[9-11]。对于该情况，通常通过设定阈值去伪，但在低信噪比条件下编码脉冲和杂波幅度相差不大，难以保证应用效果，如图5所示。对于带通滤波去噪后的信号，当阈值设定为0.036 MPa时，幅度小于0.036 MPa的波形均被置为0，只有部分杂波被消除，与编码脉冲幅度差异不大的伪峰未被消除（如52.10和82.85 s附近的杂波脉冲），仍会对后续处理造成干扰。当阈值设定为0.067 MPa时，幅度小于0.067 MPa的波形均被置为0，杂波均被消除，波形中不再存在伪峰，但19.9和167.5 s附近的同步头脉冲也被消除，无法再确定同步头。对于优化VMD分解去噪后的信号，当阈值设定为0.036 MPa时，即可完全消除杂波，并完整保留编码脉冲。

图 5 通过设定阈值去除杂波效果示意

Figure 5. Clutter removal effects through threshold setting

下载: 全尺寸图片幻灯片

根据编码规则，同步头信号中3个脉冲峰值之间的时间间隔均为4 s。计算15.3～26.3 s范围内3个连续脉冲相邻波峰之间的时间间隔，结果如图6所示。对于带通滤波去噪后的信号，相邻波峰之间的时间间隔分别为3.35和4.63 s，与理论值差异较大，难以判定为同步头信号。对于优化VMD分解去噪后的信号，相邻波峰之间的时间间隔分别为4.03和3.96 s，与理论值差异很小，可以判定为同步头信号。即，优化VMD分解算法能够更好地保留编码脉冲的特征。

图 6 15.3～26.3 s范围内3个连续脉冲相邻波峰之间的时间间隔

Figure 6. Time interval between adjacent wave peaks of three continuous pulses in the range of 15.3 ～ 26.3 s

下载: 全尺寸图片幻灯片

互相关是一种确定2个信号之间相似度的处理方法，不需要准确地获取每个有效峰的位置，其基本原理是对信号序列和相关器进行点积计算^[9,19-20]。对于本文所分析的信号，构造的理论同步头相关器如图7所示。将理论同步头相关器与去噪后的信号进行互相关处理可得相关后的波形，如图8所示。分析可知，无论是带通滤波去噪后的信号还是优化VMD去噪后的信号，互相关处理后，同步头附近的相关波形幅度均明显强于其他位置。对于带通滤波去噪后的信号，第一帧数据相关波形最大值所对应的位置为25.45 s（即第一帧数据的起始位置），第二帧数据相关波形最大值所对应的位置为172.50 s（即第二帧数据的起始位置）。对于优化VMD去噪后的信号，第一帧数据的起始位置为25.50 s，第二帧数据的起始位置为172.50 s，与利用带通滤波去噪后信号获取的起始位置基本一致。这表明，与传统基于峰值检测的同步头识别算法相比，基于互相关的同步头识别算法具有更高的稳定性。

图 7 理论同步头相关器波形

Figure 7. Waveform of theoretical synchronization correlator

下载: 全尺寸图片幻灯片

图 8 理论同步头相关器与去噪后信号通过互相关处理得到的波形

Figure 8. Waveforms obtained by cross-correlation between the theoretical synchronization correlator and the de-noised signals

下载: 全尺寸图片幻灯片

3.3 码值判别效果

起始位置确定后，即可根据数据块长度对去噪后的信号进行分块处理，每一个数据块内的波形代表着一个码值。传统的码值判别方式与传统的寻找同步头方式类似，即检测数据块内波形的峰值，计算波峰位置与数据块起始位置之间的时间间隔。这种方式同样也存在稳定性差的问题，在此不再赘述。基于图8中得到的同步头位置，对优化VMD去噪后的信号进行分块处理。对于第一帧数据，25.5～44.5 s为第一个数据块，44.5～63.5 s为第二个数据块，63.5～82.5 s为第三个数据块，82.5～101.5 s为第四个数据块，101.5～120.5 s为第五个数据块，120.5～139.5 s为第六个数据块，139.5～158.5 s为第七个数据块，如图9所示。

图 9 数据块划分结果

Figure 9. Partition results of data blocks

下载: 全尺寸图片幻灯片

根据编码规则构造理论数据块相关器，其波形如图10所示。对于每个数据块，将理论数据块相关器与数据块内去噪后的信号分别进行互相关处理，即可得到16个相关值，如图11所示。

图 10 理论数据块相关器波形

Figure 10. Waveforms of theoretical data block correlators

下载: 全尺寸图片幻灯片

分析可知，将理论数据块相关器与数据块1进行相关处理后，0x2码值对应的相关值最大，即数据块1内波形所对应的码值为0x2。同理可以得出，数据块2～7内波形所对应的码值分别为0xA、0x3、0x9、0x3、0x9和0x3。根据编码规则可知，该数据帧为复合序列，由1个同步头、1个序列号和3个GAMMA测量值3部分组成（见表1）。序列号占据1个数据块，每个GAMMA测量值占据2个数据块。因此，序列号的码值为0x2，3个GAMMA测量值的码值依次为0x3A、0x39和0x39。

表 1 数据序列编码

Table 1. Coding of data sequence

序列号	参数名称	位数	量程/API	脉冲数	精度/API
1	GAMMA	8	0～500	2	±0.977
2	GAMMA	8	0～500	2	±0.977
3	GAMMA	8	0～500	2	±0.977

下载: 导出CSV

| 显示表格

图 11 理论数据块相关器与各数据块内去噪后的信号通过互相关处理得到的曲线

Figure 11. Curves obtained by cross-correlation between theoretical data block correlators and the de-noised signals in data blocks

下载: 全尺寸图片幻灯片

根据表1所示数据序列编码规则，可以将组合后的十六进制数先转换成十进制数，再转换成井下真实的测量结果。即：

${V_{\rm{m}}} = \frac{{V_{{\rm{bin}}}} \left( {{V_{\max}} - {V_{\min }}} \right)} { {{2^D} - 1} } + {V_{\min }}$

(8)

式中：V_m为真实参数测量值，API；V_bin为十进制组合码值；V_max为最大测量值，API；V_min为最小测量值，API；D为测量值位数。

因此，该帧钻井液脉冲信号最终解码结果为：序列号为2，3个GAMMA测量值依次为113.726、111.765和111.765 API。

4. 结论与建议

1）为了满足复杂井眼环境下钻井液脉冲信号处理的要求，根据脉冲位置调制编码的基本原理，提出了一种基于优化变分模态分解（VMD）和互相关的钻井液脉冲信号处理方法。利用该方法，实现了低信噪比条件下有用信号的有效提取、数据帧起始位置的可靠计算以及码值的准确获取。

2）与传统的带通滤波去噪算法相比，优化VMD算法能够更好地压制杂波、保留编码脉冲的特征。与传统的阈值设定和峰值检测识别算法相比，互相关算法不需要准确地获取每个有效峰的位置，具有更高的稳定性。

3）目前，VMD算法具有较大的计算量，建议下一步对算法进行并行化处理，以提高解码效率。

图 1 整体式卡瓦的结构尺寸

Figure 1. Structure and size of the integral slip

下载: 全尺寸图片幻灯片

图 2 整体式卡瓦张开示

Figure 2. Open diagram of the integral slip

下载: 全尺寸图片幻灯片

图 3 整体式卡瓦断裂形状

Figure 3. Fracture shape of the integral slip

下载: 全尺寸图片幻灯片

图 4 国标试件尺寸

Figure 4. The size of national standard specimen

下载: 全尺寸图片幻灯片

图 5 数值模拟模型

Figure 5. Numerical simulation model

下载: 全尺寸图片幻灯片

图 6 材料a和b加工的整体式卡瓦的应力分布

Figure 6. Stress distribution of the integral slip of Material a and Material b

下载: 全尺寸图片幻灯片

图 7 应力槽的应力分布

Figure 7. Stress distribution of the stress groove

下载: 全尺寸图片幻灯片

图 8 应力槽结构示意

Figure 8. Schematic diagram of the stress groove structure

下载: 全尺寸图片幻灯片

图 9 锥体反作用力和卡瓦的Mises应力模拟结果

Figure 9. Simulation results of Mises stress distribution of cone reaction force and slip

下载: 全尺寸图片幻灯片

图 10 模拟模型及网格划分

Figure 10. Simulation model and grid partition

下载: 全尺寸图片幻灯片

图 11 卡瓦断裂过程

Figure 11. Fracture process of slip

下载: 全尺寸图片幻灯片

图 12 卡瓦断裂试验结果

Figure 12. Experiment results of slip fracture

下载: 全尺寸图片幻灯片

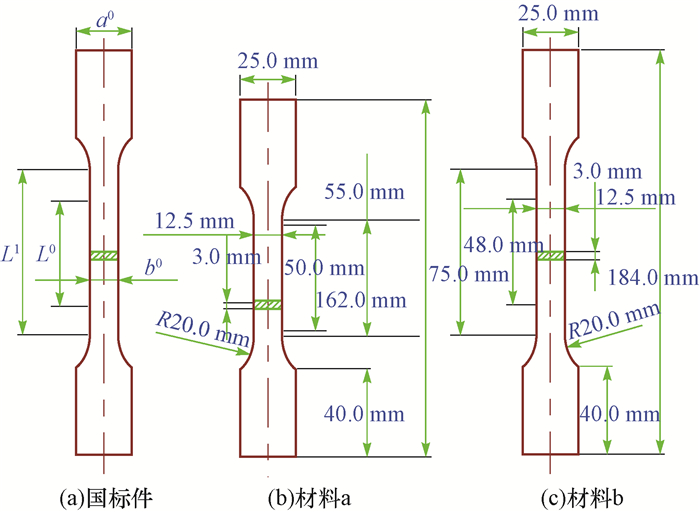
表 1 材料a和b的力学性能参数

Table 1 Mechanics parameters of Material a and Material b

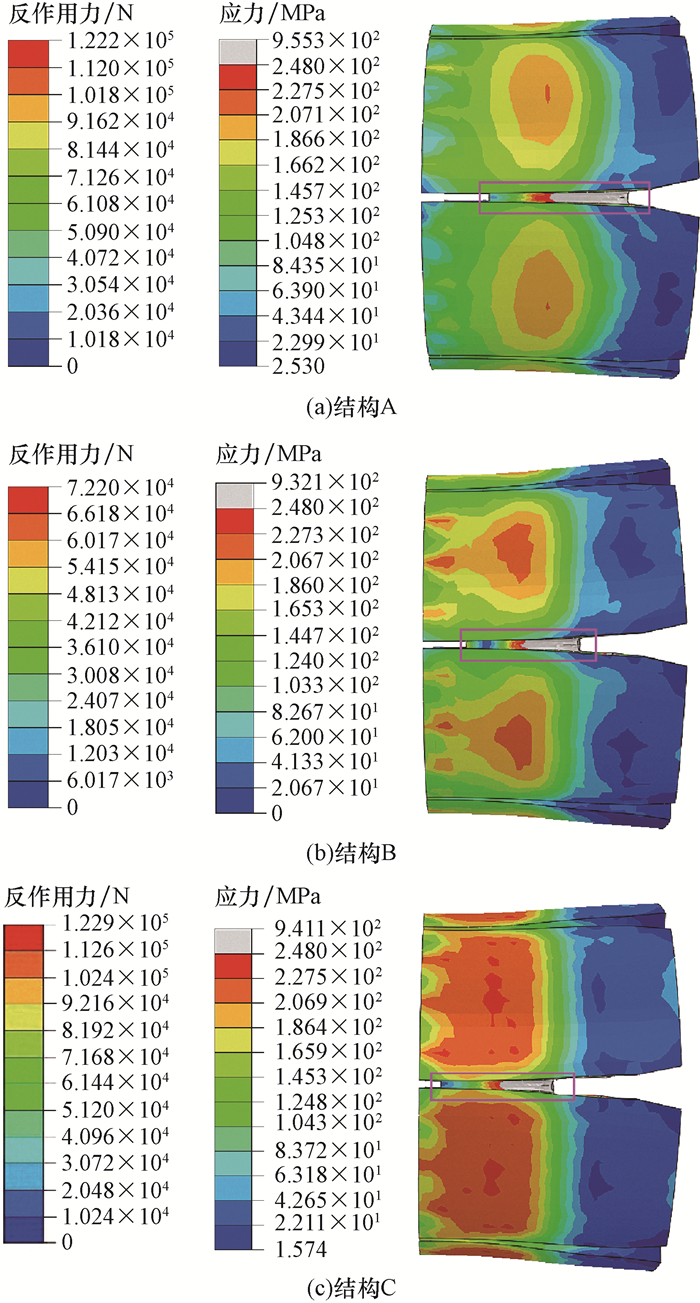
材料	弹性模量/ MPa	泊松比	屈服强度/ MPa	抗拉强度/ MPa
a	5 615	0.25	201.31	248
b	7 843	0.25	148.00	215

下载: 导出CSV

表 2 应力槽结构参数

Table 2 Structural parameters of the stress groove

结构	前端距/mm	后端距/mm
A	15.0	20.0
B	25.0	10.0
C	30.0

下载: 导出CSV

参考文献(16)

[1]	HAMMERLINDL D J.Movement, forces, and stresses associated with combination tubing strings sealed in packers[J].Journal of Petroleum Technology, 1977, 29(2):195-208. doi: 10.2118/5143-PA
[2]	SHAHANI A R, SHARIFI S.Contact stress analysis and calculation of stress concentration factors at the tool joint of a drill pipe[J].Materials & Design, 2009, 30(9):3615-3621.
[3]	LIN Z C.The strength analysis and structure optimization of packer slip based on ANSYS[J].Applied Mechanics and Materials, 2013, 423/424/425/426:1967-1971. http://www.scientific.net/AMM.423-426.1967
[4]	CAI Maojia, CAO Yinping, WANG Xin, et al.Analysis of interaction between HTHP completion packer's slip and the casing wall[J].Applied Mechanics and Materials, 2013, 423-426:866-870. doi: 10.4028/www.scientific.net/AMM.423-426
[5]	祝效华, 晁圣棋, 刘祖林, 等.基于试验和数值仿真的封隔器卡瓦结构优化[J].系统仿真学报, 2016, 28(11):2729-2735. http://d.old.wanfangdata.com.cn/Periodical/xtfzxb201611012 ZHU Xiaohua, CHAO Shengqi, LIU Zulin, et al.Structural optimization of packer slips based on experimental and numerical simulation[J].Journal of System Simulation, 2016, 28(11):2729-2735. http://d.old.wanfangdata.com.cn/Periodical/xtfzxb201611012
[6]	刘景超, 王晓, 马认琦, 等.整体式卡瓦断裂压力的试验研究[J].钻采工艺, 2016, 39(4):67-69. doi: 10.3969/J.ISSN.1006-768X.2016.04.20 LIU Jingchao, WANG Xiao, MA Renqi, et al.Experimental study on fracture pressure of integral slips[J].Drilling & Production Technology, 2016, 39(4):67-69. doi: 10.3969/J.ISSN.1006-768X.2016.04.20
[7]	王迪, 何世平, 张熹.封隔器卡瓦接触应力研究[J].实验力学, 2006, 21(3):351-356. doi: 10.3969/j.issn.1001-4888.2006.03.015 WANG Di, HE Shiping, ZHANG Xi. Study on contact stress of packer slips[J].Experimental Mechanics, 2006, 21(3):351-356. doi: 10.3969/j.issn.1001-4888.2006.03.015
[8]	邓民敏.封隔器用整体式卡瓦设计原理与设计方法的研究[D].北京: 石油大学(北京), 1998: 47-52. DENG Minmin.Study on the design principle and design method of integral slips for packers[D].Beijing: University of Petroleum(Beijing), 1998: 47-52.
[9]	何霞, 李明, 王国荣, 等.悬挂封隔器卡瓦作用区段套管应力分布研究[J].应用数学和力学, 2017, 38(9):1021-1028. http://d.old.wanfangdata.com.cn/Periodical/yysxhlx201709006 HE Xia, LI Ming, WANG Guorong, et al.Study on the stress distribution of the casing section of the suspended packer slip section[J].Applied Mathematics and Mechanics, 2017, 38(9):1021-1028. http://d.old.wanfangdata.com.cn/Periodical/yysxhlx201709006
[10]	张俊亮, 刘汝福, 李丽云, 等.整体式卡瓦牙型结构优化及试验研究[J].石油机械, 2012, 40(6):83-86. http://www.cnki.com.cn/Article/CJFDTotal-SYJI201206021.htm ZHANG Junliang, LIU Rufu, LI Liyun, et al.Optimization and experimental study of integral slips type[J].China Petroleum Machinery, 2012, 40(6):83-86, 97. http://www.cnki.com.cn/Article/CJFDTotal-SYJI201206021.htm
[11]	喻冰, 赵维斌, 雷璐侨, 等.非金属桥塞镶齿卡瓦的有限元分析及优化[J].石油机械, 2013, 41(8):68-70, 75. doi: 10.3969/j.issn.1001-4578.2013.08.017 YU Bing, ZHAO Weibin, LEI Luqiao, et al.Finite element analysis and optimization of non-metallic bridge plug toothed slips[J].China Petroleum Machinery, 2013, 41(8):68-70, 75. doi: 10.3969/j.issn.1001-4578.2013.08.017
[12]	马认琦, 孔学云, 鞠少栋, 等.海上完井封隔器新型锚定卡瓦咬入套管分析[J].石油机械, 2014, 42(9):65-68. doi: 10.3969/j.issn.1001-4578.2014.09.016 MA Renqi, KONG Xueyun, JU Shaodong, et al.Analysis of new anchoring slips of packer for offshore completion[J].China Petroleum Machinery, 2014, 42(9):65-68. doi: 10.3969/j.issn.1001-4578.2014.09.016
[13]	高志华, 魏江兵, 张涔, 等.利用应变片测量金属弹性模量[J].物理与工程, 2017, 27(2):37-41, 46. doi: 10.3969/j.issn.1009-7104.2017.02.008 GAO Zhihua, WEI Jiangbing, ZHANG Cen, et al.Using strain gauge to measure elastic modulus of metals[J].Physics and Engineering, 2017, 27(2):37-41, 46. doi: 10.3969/j.issn.1009-7104.2017.02.008
[14]	匡博.盘式制动器制动噪声有限元分析[D].长沙: 湖南大学, 2013: 11-12. KUANG Bo.Finite element analysis of disc brakenoise[D].Changsha: Hunan University, 2013: 11-12.
[15]	聂洪波.三点弯曲法测试硬质合金弹性模量[J].粉末冶金材料科学与工程, 2010, 15(6):606-610. doi: 10.3969/j.issn.1673-0224.2010.06.012 NIE Hongbo.Measurement of elastic modulus of cemented carbide by three-point bending[J].Materials Science and Engineering of Powder Metallurgy, 2010, 15(6):606-610. doi: 10.3969/j.issn.1673-0224.2010.06.012
[16]	陈毅彬, 周建忠, 黄舒, 等.基于ABAQUS的激光板料成形的数值模拟研究[J].应用激光, 2007, 27(3):175-180. doi: 10.3969/j.issn.1000-372X.2007.03.003 CHEN Yibin, ZHOU Jianzhong, HUANG Shu, et al.Numerical simulation of laser sheet metal forming based on ABAQUS[J].Applied Laser, 2007, 27(3):175-180. doi: 10.3969/j.issn.1000-372X.2007.03.003

施引文献(19)

期刊类型引用(17)

1.	邓华根，韩成，王应好. 海上页岩油探井测试大规模压裂技术及实践. 化学工程与装备. 2025(02): 38-42 . 百度学术
2.	刘彝，余成林，李云子，姜喜梅，于洋洋，吴均，刘京. 压裂用有机硅暂堵转向剂的制备及性能评价. 钻井液与完井液. 2025(02): 275-282 . 百度学术
3.	刘臣，卢海兵，陈钊，葛婧楠，孙挺. 大段多簇压裂改造技术优化与页岩气储层分析应用. 粘接. 2024(04): 121-124 . 百度学术
4.	王遵察，程万，艾昆，胡清海，石育钊. 井工厂井网部署与压裂模式发展现状与展望. 钻探工程. 2024(03): 9-19 . 百度学术
5.	戴佳成，李根生，孙耀耀，李敬彬，王天宇. 基于水平井的径向井开采页岩油产能模拟和参数分析. 石油科学通报. 2024(04): 604-616 . 百度学术
6.	杨南鹏，范雨航，高彬，张世锋. 暂堵技术在致密砂岩气藏压裂中的应用. 能源与环保. 2023(01): 168-174 . 百度学术
7.	邹龙庆，何怀银，杨亚东，龚新伟，肖剑锋，苌北. 页岩气水平井暂堵球运移特性数值模拟研究. 石油钻探技术. 2023(05): 156-166 . 本站查看
8.	侯冰，张其星，陈勉. 页岩储层压裂物理模拟技术进展及发展趋势. 石油钻探技术. 2023(05): 66-77 . 本站查看
9.	戴佳成，王天宇，田康健，李敬彬，田守嶒，李根生. 页岩油储层径向井立体压裂产能预测模型研究. 石油科学通报. 2023(05): 588-599 . 百度学术
10.	滕卫卫，古小龙，王博，张谷畅，吴宝成，李建民，葛洪魁. 段内多簇暂堵压裂中暂堵球直径优化研究. 钻采工艺. 2023(05): 61-67 . 百度学术
11.	董小卫，田志华，李一强，汪志，韩光耀，唐家财，刘帅. 水平井桥塞分段压裂管外光纤监测技术. 石油钻采工艺. 2023(05): 649-654 . 百度学术
12.	陈志明，赵鹏飞，曹耐，廖新维，王佳楠，刘辉. 页岩油藏压裂水平井压–闷–采参数优化研究. 石油钻探技术. 2022(02): 30-37 . 本站查看
13.	蔡萌，唐鹏飞，魏旭，刘宇，张浩，张宝岩，耿丹丹. 松辽盆地古龙页岩油复合体积压裂技术优化. 大庆石油地质与开发. 2022(03): 156-164 . 百度学术
14.	樊平天，刘月田，冯辉，周东魁，李平，周丰，秦静，余维初，史黎岩. 致密油新一代驱油型滑溜水压裂液体系的研制与应用. 断块油气田. 2022(05): 614-619 . 百度学术
15.	王成俊，张磊，展转盈，倪军，高怡文，王维波. 基于裂缝介质转变为多孔颗粒介质的调剖方法与矿场应用. 断块油气田. 2022(05): 709-713 . 百度学术
16.	李臻，李真，程嘉瑞，崔璐. 高速射流孔眼冲刷腐蚀扩孔规律试验研究. 石油化工腐蚀与防护. 2022(05): 1-5+41 . 百度学术
17.	李臻，李真，程嘉瑞，崔璐. 高速射流孔眼冲刷腐蚀扩孔规律实验研究. 山东化工. 2022(20): 1-4+8 . 百度学术

其他类型引用(2)

资源附件(0)

图(12) / 表(2)

计量

文章访问数: 10024
HTML全文浏览量: 5491
PDF下载量: 101
被引次数: 19

1. 传统信号处理方法及其不足
2. 改进的信号处理方法
3. 传统方法与改进方法的对比分析
3.1 去噪效果
3.2 同步头识别效果
3.3 码值判别效果
4. 结论与建议

可溶桥塞整体式卡瓦结构优化设计

作者简介: 郝地龙(1993—)，男，云南曲靖人，2017年毕业于长春大学机械工程专业，在读硕士研究生，主要从事封隔器设计方面的研究工作。E-mail:2608083214@qq.com

计量

出版历程