2. 中国石油大学(北京)石油工程学院, 北京 102249
2. College of Petroleum Engineering, China University of Petroleum(Beijing), Beijing, 102249, China
目前稠油热采的主要方式包括火驱、蒸汽驱、蒸汽吞吐和蒸汽辅助重力泄油(steam assisted gravity drainage,简称SAGD)技术,其中SAGD是最有效的稠油开采方式[1-4]。SAGD开采主要分为循环预热及生产2个阶段。循环预热时同时向上下平行的2口水平井井筒注220~250 ℃蒸汽并使其循环,通过热传导、热对流方式加热井筒附近油藏,逐步降低原油黏度,使上、下水平井(间隔5.00 m)附近区域的超稠油流动,形成包围上、下水平井的蒸汽腔体,为生产阶段稠油的流动提供条件,该过程持续几个月至一年左右[5]。在生产阶段,上井(简称为I井)持续注汽,下井(简称为P井)转为生产井持续采油,井周流动原油在蒸汽压力和重力同时驱动下沿平行于倒水滴状蒸汽腔外缘方向流向生产井,该过程可持续几年至几十年[5-8]。
新疆西北部准噶尔盆地风城油田拥有丰富的陆相稠油资源,储量预计超过3.6×108t,其中超稠油在50 ℃下的黏度为1.92×103~1.15×106 mPa·s,储层埋深160.00~700.00 m,原位状态下完全不流动。风城油田超稠油油藏具有富泥质/泥岩夹层发育、渗透率低和非均质性强的特点[3],导致循环预热周期长、蒸汽能耗大、见汽周期长、产出液处理污泥含量高且回收困难和环境保护压力大等一系列工程问题,严重制约了SAGD预热及开发效果[5, 8-9]。为了解决这些问题,Yuan Yanguang等人[10-11]、Lin Botao等人[12-13]提出和完善了挤液扩容预处理储层改造技术(亦称“微压裂”技术)。基于油砂的力学本构和渗流特征,采用有限元方法来计算特定井口排量或压力、几何参数、地质边界条件下的储层变形和渗流,才能有效应用该技术来设计现场的挤液施工参数或预测已施工井的挤液扩容效果。作者曾提出通过连通系数来定量评价储层整体扩容效果的方法[12],然而每口SAGD井施工时都需要根据特定参数重新进行有限元建模来计算连通系数,现场应用较为困难和不便。
为此,笔者采用连通系数作为定量描述扩容效果的指标,利用92个有限元算例分析了储层的岩石物理性质、油藏几何参数和挤液施工排量等3类因素影响连通系数的规律,扩充了连通系数的数据库;并基于该数据库绘制了多因素影响SAGD井挤液扩容效果的分析图版,应用该图版对3口SAGD井连通系数进行了快速分析。
1 挤液扩容储层改造技术原理循环预热注蒸汽前实施挤液扩容储层改造技术,通过控制井口流量或压力方式,逐级提压使井筒与地层产生压差,从而对井周储层挤液;在井筒附近区域形成张性微裂缝,并使升高的孔隙压力从井筒向地层不断扩散;同时结合地应力差的作用,以剪切扩容(剪胀)和张性扩容2种力学机理扩大地层孔隙体积[9-13](见图 1)。该作用增强了井筒附近区域的流体渗流,增加了井间渗流通道(水力连通),促进了循环预热期间的热对流效应(热力连通),能够大幅缩短预热周期,节约注汽成本,减小产出液处理压力,并提前启动后期生产阶段[12-14]。
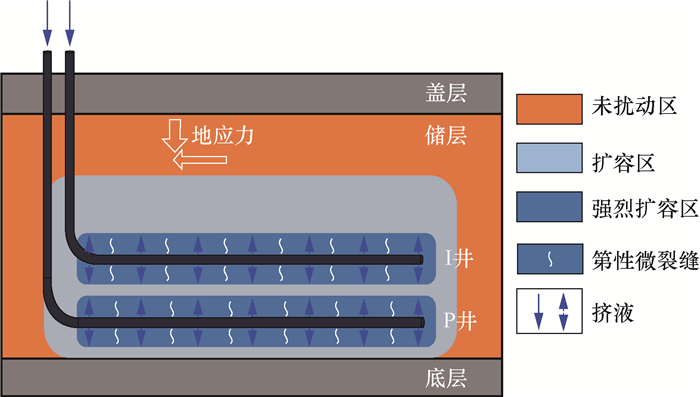
|
| 图 1 超稠油储层挤液扩容示意 Fig.1 Schematic diagram of squeezing fluid and capacity expansion in ultra-heavy oil reservoirs |
稠油储层的挤液扩容可视为在井筒与地层压差下地层孔隙压力从井筒向储层纵深逐步扩散的过程,其力学机制包括孔隙流体(挤入液)的热膨胀、流体受力压缩和基质骨架的体积变形[11, 15]:
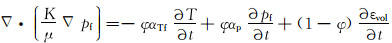
|
(1) |
式中:K为流体的有效渗透率,D;μ为流体黏度,Pa·s;pf为地层孔隙流体压力(简称孔压),Pa;ϕ为孔隙度;αTf为孔隙流体的热膨胀系数,K-1;T为温度,K;αp为孔隙流体的压缩系数,Pa-1;εvol为骨架的体积应变。
由于挤入液为前期SAGD施工产出的冷凝水,K即为水的有效渗透率。挤入液温度为20~70 ℃,但其在挤液过程中的变化幅度小,式(1)右侧第一项可略去。此外,挤入液的温度对储层的力学参数和渗流特征有一定的影响,但其对以连通系数为指标的扩容效果的影响可忽略不计[12-13],因此暂不考虑挤入液温度的影响(默认其为20 ℃)。
2.1 有限元计算方法通常,基于Drucker-Prager弹塑性本构模型描述油砂的力学本构[10-12, 16-17]:
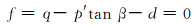
|
(2) |
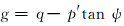
|
(3) |
式中:f为屈服面函数,Pa;p′为平均有效应力,Pa;q为米泽斯应力,Pa;β为摩擦角,(°);d为黏聚力,Pa;g为塑性势函数,Pa;ψ为剪胀角,(°)。
油砂储层中水的有效渗透率随扩容或压缩的变化可近似用Kozeny-Poiseuille方程拟合试验数据获取[7]:
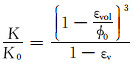
|
(4) |
式中:K0为水的初始有效渗透率,D;εv为水的体积应变;ϕ0为初始孔隙度。
式(1)—式(4)构成了描述挤液扩容对应的流固耦合机理的基本方程组。
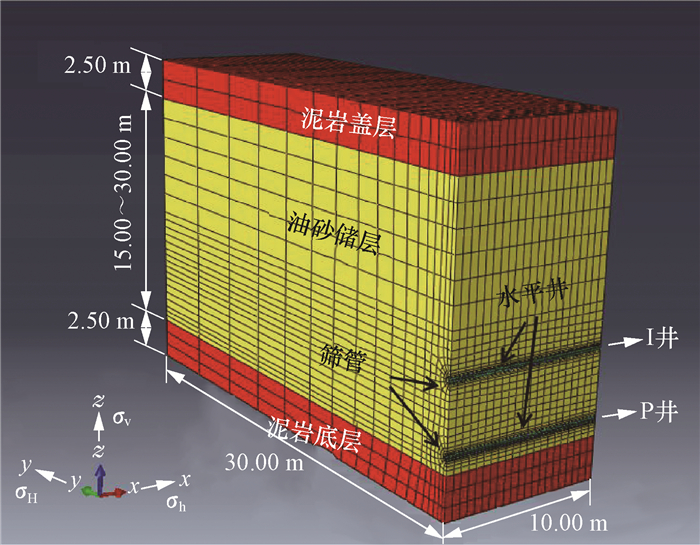
挤液扩容的通用有限元计算模型如图 2所示。15.00~30.00 m厚的油砂储层夹在泥岩盖层和底层之间,有限元计算设置泥岩厚度为2.50 m。几何模型取水平段长度10.00 m的部分,且为轴对称模型的一半(连接I井、P井垂线的一侧)。由于储层周围为无限大空间,模型四周约束法向位移,底面约束三向位移;筛管内表面设置为渗流边界条件,其余面均设置为不渗流面(泥岩几乎不透水,且模型沿y向延伸长度满足渗流计算要求)。设三向地应力σh,σH和σv方向分别为x,y, z方向,双水平井沿x方向(现场设计水平井尽量沿x方向,以获取最大扩容范围)。泥岩盖层顶面允许z方向位移并施加上覆岩层压力[12]。
|
| 图 2 储层挤液扩容有限元计算模型 Fig.2 Finite element calculation model for squeezing liquid and capacity expansion |
因此,基于室内试验获得的储层及夹层的力学本构参数、渗流参数,结合现场地质资料确定几何参数和地质边界条件,可依据给定的井筒压力或排量定量预测储层的变形及渗流随挤液时间的变化情况。
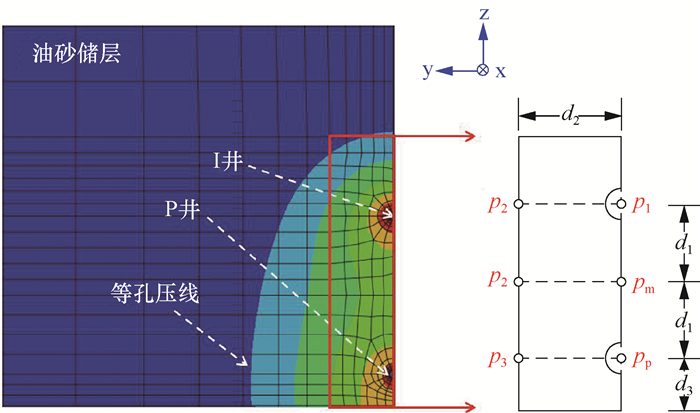
2.2 挤液扩容效果评价方法典型的挤液扩容所致孔压分布呈现以I井、P井中心连线为长轴的半椭圆状,底部被泥岩截断(见图 3)[12]。挤液扩容的主要目的是建立I井、P井的水力连通,使井间形成温度、压力快速响应的高渗扩容带,以使后期注蒸汽加热时能迅速形成包围I井、P井的蒸汽腔,显著缩短预热周期[9, 12]。由此,Lin Botao等人[12]建立了计算连通系数(记为CP)的计算公式:
|
| 图 3 计算连通系数时的孔隙压力分布情况 Fig.3 Pore pressure distribution plot for calculating the connectivity coefficient |
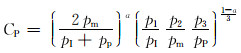
|
(5) |
式中:pI和pp分别为利用有限元法计算出的I井、P井的井底压力超过初始值的部分(超静水压力),MPa;pm为计算出的两井间中点处的超静孔隙水压力, MPa;p1,p2和p3分别为距离I井、距离两井中点和距离P井均为d2(一般取2.00 m[12])处的超静孔隙水压力,MPa;a为评价水平方向相对垂直方向连通程度的权重系数,一般取0.5[12];d1为两井间隔距离(通常为5.00 m)的一半,m。
式(5)右边的第一部分表示两井中部的超静孔隙水压力相对两井的平均超静水压力的大小;第二部分表示距井筒一定距离的超静孔隙水压力相对井筒和两井中点处的超静水/超静孔隙水压力的大小。当I井、P井完全连通时,图 3方框内的超静孔隙水压力处处相等,连通系数为1.0;当完全不连通时,要挤入地层的液体在井筒憋压而无法传递到地层,连通系数为0。根据该方法在新疆风城油田12口SAGD井挤液施工的应用经验,一般来说当连通系数大于0.6时,可认为I井、P井的连通效果较好[12, 18]。
3 扩容效果影响因素分析 3.1 基准算例分析应用上述方法,在作者前期研究的基础上[3, 9, 12-13, 17-18],首先对新疆风城油田重18区某SAGD井挤液扩容进行了有限元分析,并将其作为下文多因素分析的基准算例。该SAGD井水平段长500.00 m,储层厚度30.00 m,I井垂深453.00 m,P井垂深458.00 m,P井距底部泥岩层1.00 m。结合测井资料、小型压裂试验和Kaiser声发射试验,测得该区块三向地应力σv,σH和σh随深度变化的梯度为0.021,0.018和0.015 MPa/m。试验测得泥岩盖层及底层的杨氏模量为1.7 GPa,泊松比为0.2(泥岩采用线弹性模型),水的有效渗透率为2 μD。该井采用筛管完井方式,筛管杨氏模量为20 GPa,泊松比为0.2,设为完全透水状态(K取20 D)[12]。储层的原油密度为0.955 kg/L,50 ℃下原油黏度为7 784 mPa·s,原油含量为8.7%,泥质含量为9.2%,含油饱和度为49%,孔隙度为32.5%,弹性模量为652 MPa,泊松比为0.4,内摩擦角为46°,黏聚力为1.8 MPa,剪胀角为25°,水的初始垂向有效渗透率K0_v为882 μD,水的初始水平向有效渗透率K0_h为441 μD[9]。
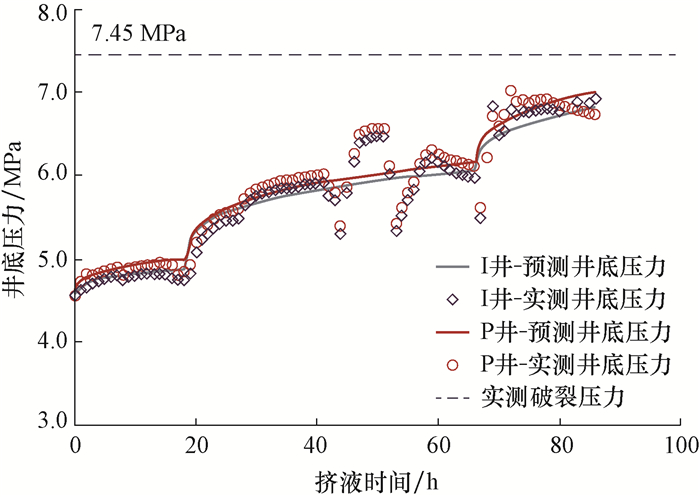
现场通常采取控制排量的方式进行挤液,分2~ 3个阶段提升井底压力,并控制其升至小于地层破裂压力0.5 MPa左右,采用控压挤注和提压改造实施方式,持续时间为3~4 d。该SAGD井挤液的实施方式为:0~18 h阶段,I井4.5 m3/d,P井5.3 m3/d;19~66 h阶段,I井18.2 m3/d,P井13.1 m3/d;67~86 h阶段,I井27.3 m3/d,P井21.3 m3/d。86 h后观测发现排量迅速增大,根据现场经验初步判断I井、P井已建立水力连通,并得到了井底压力随挤液时间的变化曲线(见图 4)。
|
| 图 4 井底压力随挤液时间的变化 Fig.4 Variation of bottom hole pressure with the time of squeezing liquid |
从图 4可以看出,根据室内试验测得的参数和现场地应力条件、施工排量,采用有限元方法预测的I井和P井的井底压力与实测值基本一致。挤液结束后,计算得到的连通系数为0.48,表明该井挤液扩容改造的效果较差。循环预热施工显示该井预热周期为100 d。下面以该井的分析结果作为基准,分析不同因素对连通系数的影响。
3.2 影响因素类型挤液扩容的效果主要取决于3类因素:储层的岩石物理性质、储层的几何参数和现场的挤液施工排量。根据现场资料,基于3类因素的可能变化范围,设定了有限元计算的影响因素变化范围(包含基准算例参数,见表 1)。由于同一区块的地应力变化不大,且地应力对疏松储层的孔隙弹性力学行为基本无影响[13],暂不考虑其对连通系数的影响。
| 因素 | 参数 | 不同级别取值 | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| 岩石物理性质 | 杨氏模量/MPa | 300 | 650 | 1 000 | 1 350 | |
| 泊松比 | 0.1 | 0.2 | 0.3 | 0.4 | ||
| 摩擦角/(°) | 35 | 40 | 45 | 50 | 55 | |
| 黏聚力/MPa | 0.2 | 0.6 | 1.0 | 1.4 | 1.8 | |
| 剪胀角/(°) | 15 | 20 | 25 | 30 | 35 | |
| 垂向渗透率/mD | 0.22 | 0.44 | 0.88 | 1.76 | 3.52 | |
| 横向垂向渗透率比值 | 0.25 | 0.50 | 1.00 | 2.00 | 4.00 | |
| 孔隙度,% | 27.5 | 30.0 | 32.5 | 35.0 | 37.5 | |
| 储层几何参数 | 储层埋深/m | 200.00 | 455.50 | 600.00 | ||
| 井底距/m | 1.00 | 2.50 | 5.00 | |||
| 储层厚度/m | 14.50 | 17.50 | 21.50 | 23.50 | ||
| 挤液施工参数 | 平均日排量/(m3·d-1) | 10 | 20 | 31 | 40 | 50 |
| 注:井底距为P井到泥岩底层的距离。 | ||||||
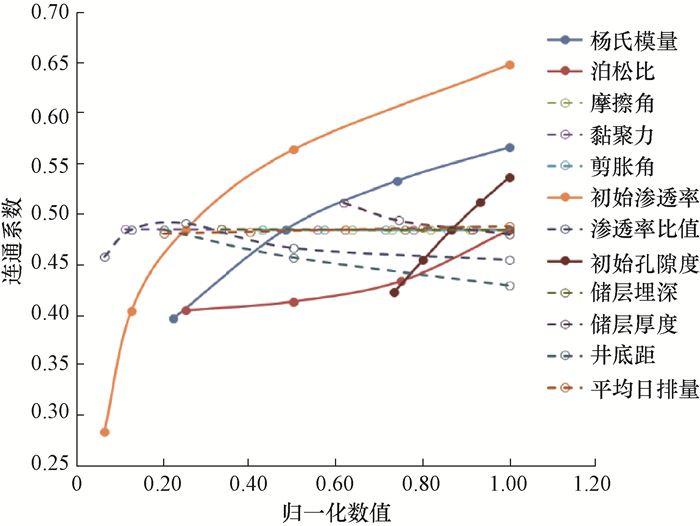
根据基准算例,根据表 1中的各因素取值,分析该因素对连通系数的影响,计算了42个有限元算例。依据算例结果,可获取连通系数随各因素归一化数值(各因素除以表 1中的最大值)的变化情况,结果如图 5所示。
|
| 图 5 连通系数随归一化数值的变化曲线 Fig.5 The change of the connectivity coefficient with normalized values |
由图 5可知,摩擦角、黏聚力和剪胀角对连通系数没有影响。这是因为, 正常施工排量导致的地层孔隙压力不足以使井筒附近储层产生塑性屈服。由于连通系数同时考虑了横向和纵向的连通性(见式(5)),横纵渗透率比值对连通系数几乎没有影响。此外,连通系数随储层埋深、储层厚度和井底距的变化幅度小于0.05,因此亦忽略不计。需要特别指出的是,考虑投资效益、人力安排和设备需求,现场挤液施工一般为72~96 h,而施工50~60 h后连通系数基本不再变化。结合图 5可知,施工排量对连通系数基本没有影响。从图 5可见,对连通系数影响较大的因素为杨氏模量、泊松比、初始孔隙度和初始渗透率等储层岩石物理参数(图 5中实线曲线),其中初始渗透率(各方向平均值)的影响最大。
3.4 建立连通系数快速分析图版选取杨氏模量、泊松比、孔隙度和渗透率等4个影响连通系数的关键因素,将其值相对基准算例对应的参数(见表 1)作无量纲化处理,即:
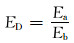
|
(6) |
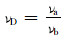
|
(7) |

|
(8) |
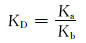
|
(9) |
式中:Ea,νa, ϕa和Ka分别为实际算例的杨氏模量、泊松比、孔隙度和水的平均有效渗透率(为各方向平均值);Eb, νb, ϕb和Kb分别为基准算例的参数。
以无量纲化处理后的ϕDKD为横轴,EDνD为纵轴,连接相同连通系数的算例点(或进行插值)形成等连通系数曲线,建立连通系数快速分析图版(见图 6)。图 6中每个点对应一个有限元算例,共92个算例,其中蓝色点表示图 5的42个算例计算结果,红色点表示继续改变横纵坐标区间计算的其他50个有限元算例。

|
| 图 6 连通系数快速分析图版 Fig.6 Rapid analysis chart with the connectivity coefficient |
图 6中浅黄色阴影部分表示油砂的参数范围不能涵盖的区域;同时,图 6中算例点的分布区间包括了油砂岩石物理参数分布的大致情况。现场可根据已有物性参数资料,基于该图版进行连通系数的线性插值,快速预测或比较不同SAGD井的扩容效果,并结合工程经验确定不同区块满足扩容要求的最低连通系数。
4 应用实例分析风城油田重1区A井储层杨氏模量为683 MPa,泊松比为0.4,孔隙度为35.4%,平均渗透率为3.720 mD。根据图 6线性插值可得其连通系数为0.72。重1区未进行挤液施工预处理的SAGD井平均预热周期为211 d,A井挤液后预热周期缩短为48 d,缩短幅度为77%。
重18区B井储层物性较差(泥质含量较高, 渗透率较低),杨氏模量为576 MPa,泊松比为0.3,孔隙度为33.7%,平均渗透率为1.025 mD,根据图 6线性插值可得其连通系数为0.47。重18区未进行挤液施工预处理的SAGD井平均预热周期为303 d,B井挤液后预热周期缩短为132 d,缩短幅度为56%。重18区的基准算例预测连通系数为0.48,挤液后预热周期缩短为100 d,缩短幅度为67%。
综合分析基准算例和A井、B井分析结果可知,预热周期缩短幅度和连通系数存在较好的正相关关系,两者比值为1.1~1.4。
5 结论与建议1) 在笔者之前建立的SAGD井挤液扩容效果定量评价方法的基础上,分析了岩石物理性质、油藏几何参数和挤液施工排量对以连通系数为指标的储层扩容效果的影响;根据考虑关键影响因素变化的92个有限元算例,建立了连通系数快速分析图版。
2) 岩石物理性质中的弹性模量、泊松比、初始孔隙度和初始渗透率对连通系数的影响较大,其中初始渗透率为主要影响因素;油藏几何参数和挤液施工排量对连通系数的影响可忽略不计。
3) 根据92个有限元算例绘制的连通系数快速分析图版,可以快速预测某一特定SAGD井挤液扩容后的连通系数。3口SAGD井的现场应用表明,连通系数越高,预热周期缩短幅度越大,且后者与前者的比值为1.1~1.4。
4) 为进一步缩短预热周期,现场可尝试采取改变挤入液的化学性质(如加酸、加表面活性剂)等措施改善井筒附近区域储层的渗透率,提高扩容后的连通系数。
| [1] |
李巍, 刘永建. 提高直井与水平井组合SAGD泄油速率技术研究[J]. 石油钻探技术, 2016, 44(2): 87-92. LI Wei, LIU Yongjian. Technologies for raising the oil drainage rate with vertical-horizontal well combinations in SAGD mode[J]. Petroleum Drilling Techniques, 2016, 44(2): 87-92. |
| [2] |
田亚鹏, 鞠斌山, 胡杰. 考虑蒸汽超覆的稠油蒸汽吞吐产能预测模型[J]. 石油钻探技术, 2018, 46(1): 110-116. TIAN Yapeng, JU Binshan, HU Jie. A productivity prediction model for heavy oil steam huff and puff considering steam override[J]. Petroleum Drilling Techniques, 2018, 46(1): 110-116. |
| [3] |
林伯韬, 陈森, 潘竟军, 等. 风城陆相超稠油油砂微压裂扩容机理实验研究[J]. 石油钻采工艺, 2016, 38(3): 359-364, 408. LIN Botao, CHEN Sen, PAN Jingjun, et al. Experimental study on dilation mechanism of micro-fracturing in continental ultra-heavy oil sand reservoir, Fengcheng Oilfield[J]. Oil Drilling & Production Technology, 2016, 38(3): 359-364, 408. |
| [4] |
AL BAHLANI A M M, BABADAGLI T.A critical review of the status of SAGD: where are we and what is next?[R].SPE 113283, 2008. https://www.researchgate.net/publication/254528030_A_Critical_Review_of_the_Status_of_SAGD_Where_Are_We_and_What_Is_Next
|
| [5] |
陈森, 窦升军, 游红娟, 等. 双水平井SAGD循环预热技术及现场应用[J]. 新疆石油天然气, 2012, 8(增刊1): 6-10. CHEN Sen, DOU Shengjun, YOU Hongjuan, et al. Application of steam recycle preheating technology to bilateral horizontal well[J]. Xinjiang Oil & Gas, 2012, 8(supplement 1): 6-10. |
| [6] |
BUTLER R M. Steam-assisted gravity drainage:concept, development, performance and future[J]. Journal of Canadian Petroleum Technology, 1994, 33(2): 44-50. DOI:10.2118/94-02-05 |
| [7] |
CHALATURNYK R, SCOTT J D.Geomechanical response of heavy oil reservoirs to the steam assisted gravity drainage process[R].SPE 37569, 1997. https://www.onepetro.org/conference-paper/SPE-37569-MS
|
| [8] |
COLLINS P M.Geomechanical effects on the SAGD process[R].SPE 97905, 2005. http://www.petroleumgeomechanics.com/papers/Collins2007_SPE97905.pdf
|
| [9] |
LIN Botao, JIN Yan, PANG Huiwen, et al. Experimental investigation on dilation mechanisms of land-facies Karamay oil sand reservoirs under water injection[J]. Rock Mechanics and Rock Engineering, 2016, 49(4): 1425-1439. DOI:10.1007/s00603-015-0817-8 |
| [10] |
YUAN Yanguang, YANG Baohong, XU Bin.Fracturing in the oil sand reservoirs[R].SPE 149308, 2011. http://www.bitcange.com/resources/technical-papers/fracturing-in-oil-sands-reservoirs/
|
| [11] |
YUAN Yanguang, XU Bin, YANG Baohong.Geomechanics for the thermal stimulation of heavy oil reservoirs: Canadian experience[R].SPE 150293, 2011. https://www.researchgate.net/publication/254535143_Geomechanics_for_the_Thermal_Stimulation_of_Heavy_Oil_Reservoirs-Canadian_Experience
|
| [12] |
LIN Botao, JIN Yan, CHEN Shengli. A criterion for evaluating the efficiency of water injection in oil sand reservoirs[J]. Journal of Petroleum Science and Engineering, 2017, 149: 322-330. DOI:10.1016/j.petrol.2016.10.056 |
| [13] |
LIN Botao, CHEN Shengli, JIN Yan. Evaluation of reservoir deformation induced by water injection in SAGD wells considering formation anisotropy, heterogeneity and thermal effect[J]. Journal of Petroleum Science and Engineering, 2017, 157: 767-779. DOI:10.1016/j.petrol.2017.07.067 |
| [14] |
黄勇, 张磊, 何小东, 等. 风城浅层油砂SAGD项目注汽压力优化[J]. 石油钻采工艺, 2016, 38(6): 848-851, 858. HUANG Yong, ZHANG Lei, HE Xiaodong, et al. Optimization of steam-injection pressures in Fengcheng shallow oil sand SAGD project[J]. Oil Drilling & Production Technology, 2016, 38(6): 848-851, 858. |
| [15] |
FJAR E, HOLT R M, RAAEN A M, et al. Petroleum related rock mechanics[M]. 2nd ed. New York: Elsevier Science, 2008: 514.
|
| [16] |
XU Bin, WONG R C K. Coupled finite-element simulation of injection well testing in unconsolidated oil sands reservoir[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(18): 3131-3149. DOI:10.1002/nag.v37.18 |
| [17] |
LIN B, CHEN S, JIN Y, et al.Evaluating constitutive models for simulation of water injection in land facies Karamay oil sand reservoirs[R].ARMA-2016-200, 2016. https://www.onepetro.org/conference-paper/ARMA-2016-200
|
| [18] |
张磊, 黄勇, 何小东, 等. 双水平井SAGD挤液预处理启动水力连通模型[J]. 西安石油大学学报(自然科学版), 2017, 32(2): 64-69. ZHANG Lei, HUANG Yong, HE Xiaodong, et al. Hydraulic connection model in squeeze preprocessing SAGD start-up[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2017, 32(2): 64-69. DOI:10.3969/j.issn.1673-064X.2017.02.0010 |


