2. 长江大学地球物理与石油资源学院, 湖北武汉 430100;
3. 长江大学电子信息学院, 湖北荆州 434023
2. College of Geophysics and Oil Resources, Yangtze University, Wuhan, Hubei, 430100, China;
3. College of Electronic Information, Yangtze University, Jingzhou, Hubei, 434023, China
电阻率测井仪器由于其固有的结构及工作环境, 其视电阻率曲线在地层界面附近往往出现极化角现象[1], 极化角的存在使地层层界面更容易分辨, 但也会造成曲线形态畸变, 且极化角在测井解释中易被误判为薄层[2], 造成油气储层准确划分、评价困难, 故对极化角进行定量校正具有现实意义。
明确极化角的影响因素是极化角定量校正的基础。截至目前, 在测井曲线极化角正演方面, 前人已做了一些研究:B.I.Anderson等人[3]通过水槽试验证实了随钻电磁波测井仪器响应曲线中极化角的存在, 与理论模拟结果非常吻合, 证明了数值模拟极化角幅值的准确性; 杨震、朱庚雪和李勇华等人[4-6]分析了随钻电磁波测井曲线极化角的形成机理, 并对围岩、井斜角等因素对极化角形态及幅值的影响进行了探讨; T.L.Wang等人[7]对随钻电磁波测井仪器进行了正演研究, 并对极化角的形成原因进行了简单阐释。但由于侧向类测井与感应类测井的工作原理不同, 上述研究的成果并不能应用于阵列侧井向测曲线极化角的解释中, 故需对侧向类测井曲线极化角的影响因素进行正演分析。为此, 笔者运用三维有限元数值模拟方法, 分析了围岩电阻率、钻井液电阻率、钻井液侵入特性、仪器特性、层厚、井径和井斜角对阵列侧向测井曲线极化角特性的影响, 总结了极化角的影响因素, 并提出了压制电阻率曲线极化角的措施, 以期为侧向类测井曲线极化角校正提供理论基础。
1 阵列侧向测井模式及地层模型 1.1 测井模式研究的阵列侧向测井仪器电极系结构如图 1所示。其电极系由主电极A0、8对监督电极(M1(M'1), M2(M'2), M3(M'3), M4(M'4), M5(M'5), M6(M'6), M7(M'7), M8(M'8))和6对屏蔽电极(A1(A'1), A2(A'2), A3(A'3), A4(A'4), A5(A'5), A6(A'6))组成, 监督电极和屏蔽电极对称地分布在主电极两侧, 每对电极之间短路连接。

|
| 图 1 阵列侧向测井仪器的电极系结构 Fig.1 Electrode system structure of array laterolog tools |
阵列侧向测井仪器共有5种工作模式, 可获得5种不同探测深度的电阻率(R1, R2, R3, R4和R5), 其中R1的探测深度最浅, R5的探测深度最深。5种探测模式下各电极满足如下电流、电位关系:
模式1:主电极A0发射主电流, 屏蔽电极A1(A'1)发射相同极性的屏蔽电流, 通过调节监督电极M1(M'1)和M2(M'2)使A0和A1(A'1)电位相同, A2(A'2), A3(A'3), A4(A'4), A5(A'5)和A6(A'6)充当回流电极。
模式2:主电极A0发射主电流, 屏蔽电极A1(A'1)和A2(A'2)发射相同极性的电流, 通过调节监督电极M1(M'1), M2(M'2), M3(M'3)和M4(M'4)使A0, A'1(A'1)和A2(A'2)电位相同, A3(A'3), A4(A'4), A5(A'5)和A6(A'6)充当回流电极。
模式3:主电极A0发射主电流, 屏蔽电极A1(A'1), A2(A'2)和A3(A'3)发射相同极性的电流, 通过调节监督电极M1(M'1), M2(M'2), M3(M'3), M4(M'4), M5(M'5)和M6(M'6)使A0, A'1(A'1), A2(A'2)和A3(A'3)电位相同, A4(A'4), A5(A'5)和A6(A'6)充当回流电极。
模式4:主电极A0发射主电流, 屏蔽电极A1(A'1), A2(A'2), A3(A'3)和A4(A'4)发射相同极性的电流, 通过调节监督电极M1(M'1), M2(M'2), M3(M'3), M4(M'4), M5(M'5), M6(M'6), M7(M'7)和M8(M'8)使A0, A1(A'1), A2(A'2), A3(A'3)和A4(A'4)电位相同, A5(A'5)和A6(A'6)充当回流电极。
模式5:主电极A0发射主电流, 屏蔽电极A1(A'1), A2(A'2), A3(A'3), A4(A'4)和A5(A'5)发射相同极性的电流, 通过调节监督电极M1(M'1), M2(M'2), M3(M'3), M4(M'4), M5(M'5), M6(M'6), M7(M'7)和M8(M'8)使A0, A1(A'1), A2(A'2), A3(A'3), A4(A'4)和A5(A'5)电位相同, A6(A'6)电极充当回流电极。
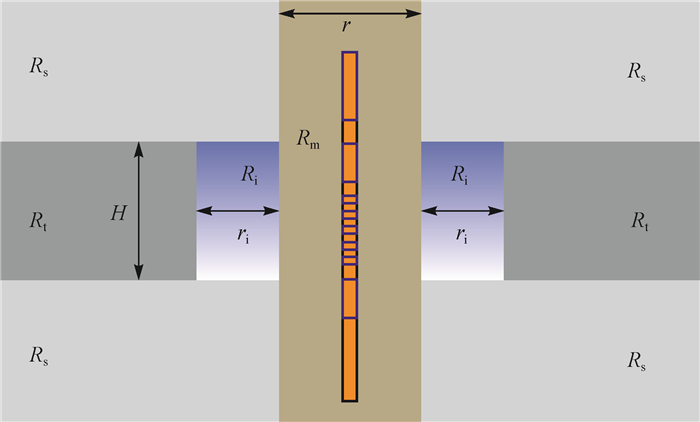
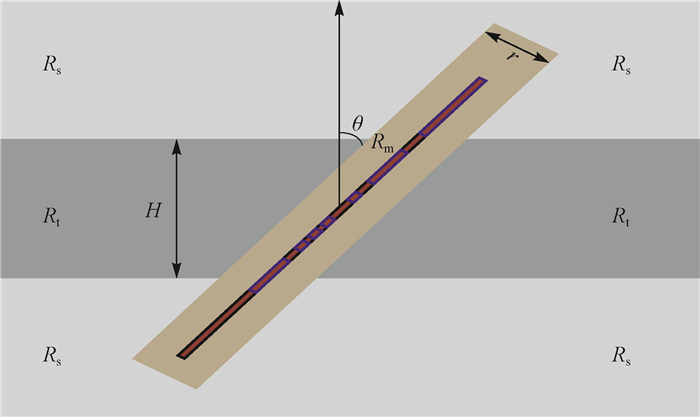
1.2 地层模型为明确阵列侧向测井视电阻率曲线极化角的影响因素, 根据实际测井环境, 分别建立了阵列侧向测井直井模型(二维模型)(见图 2)、阵列侧向测井斜井模型(三维模型)(见图 3), 研究围岩电阻率、钻井液电阻率、钻井液侵入特性、仪器特性、层厚、井径和井斜角对极化角特性的影响(图 2和图 3中:H为地层厚度, m; r为井径, m; Rt为目的层电阻率, Ω·m; Rs为围岩电阻率, Ω·m; Rm为钻井液电阻率, Ω·m; Ri为侵入带电阻率, Ω·m; ri为侵入半径, m; θ为井斜角, (°))。模型坐标系原点位于地层中心, 地层中心以上为负轴、以下为正轴, 模拟测井仪器从负轴向正轴移动时在目的层附近的正演响应。
|
| 图 2 阵列侧向测井直井模型 Fig.2 Model of array laterolog in vertical well |
|
| 图 3 阵列侧向测井斜井模型 Fig.3 Model of array laterolog in inclined well |
由于侧向类测井普遍采用频率比较低的交流电, 故可近似当作直流电来处理[8]。确定阵列侧向测井的响应, 就是要求求出一个连续而光滑的电位函数μ[9], 其在一定条件下满足:
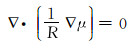
|
(1) |
式中:R为地层不同区域的电阻率, Ω·m, 根据研究区域的不同R取不同的值; μ为电位函数, V。
满足的边界条件:
1) 第一类边界条件, 在恒压电极上μ为已知常数, 在恒流电极上μ为未知常数;
2) 第二类边界条件, 在恒流电极表面满足:
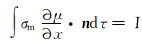
|
(2) |
式中:τ为整个电极的表面积, m2; n为屏蔽电极表面电位的垂向矢量; I为特定电极发出的电流, A; σm为钻井液电导率, S/m。
3) 在绝缘边界上, 满足:
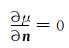
|
(3) |
式(1)与上述边界条件联立形成定解问题, 利用三维有限元法求解该定解问题, 即可求得阵列侧向测井的正演响应。
利用三维有限元方法可以计算阵列侧向测井的响应, 并可以将问题归结为求泛函数φ的极值问题[10]:
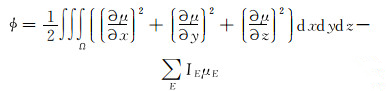
|
(4) |
式中:IE为电极发出的电流, A; μE为电极上的电位, V; Ω为积分区间, 具体指仪器表面和无穷远边界包围的空间; E为电极个数。
对所有电极进行求和, 利用前线解法可实现该极值问题的快速求解。
采用四面体单元进行网格剖分。由于斜井中的部分元素跨越了地层剖面而被重新剖分, 形成了新的四面体, 此时通过交叉网格剖分法, 即四边形之间的划分方法相互交错可实现斜井地层中的网格剖分, 具体处理方式见文献[11]。实际模拟过程中, 阵列侧向测井5种探测模式的电场可由7个分场叠加形成, 即给每个分场分配不同的加权系数, 进行电场叠加合成总电场。
3 极化角影响因素分析分析围岩电阻率、钻井液电阻率、钻井液侵入带特性、测井仪器特性、井径和层厚对阵列侧向测井曲线极化角特性的影响时, 采用如图 2所示模型; 分析井斜角对阵列侧向测井曲线极化角特性的影响时, 采用如图 3所示模型。围岩无限大, 测井仪器在井眼中居中。
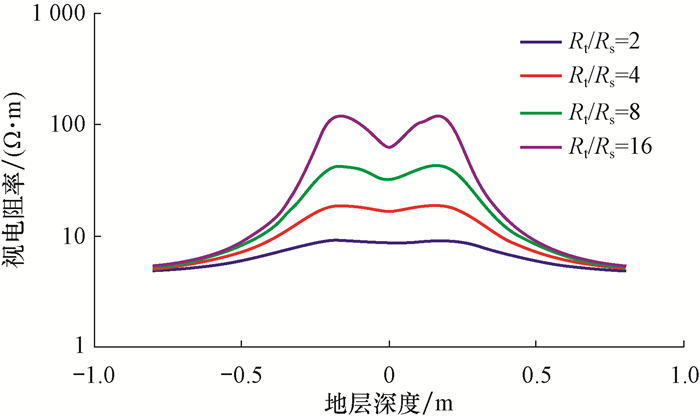
3.1 围岩电阻率在Rs=5 Ω·m, r=0.203 4 m, H=1.00 m和Rm=1 Ω·m的条件下, 分别模拟目的层电阻率与围岩电阻率的比Rt/Rs为2, 4, 8和16时阵列侧向测井曲线极化角的响应特征。由于模式1至模式5极化角特性受围岩电阻率的影响规律基本一致, 故以模式1为例进行分析, 具体模拟结果见图 4。
|
| 图 4 围岩电阻率对阵列侧向测井曲线极化角的影响 Fig.4 Effect of resistivity of surrounding rock on the polarizing angle of array laterolog curve |
由图 4可知, 围岩电阻率变化对阵列侧向测井曲线极化角特性影响较大。Rt/Rs越大, 极化角越尖锐且幅值(极化角峰顶与地层中心的视电阻率值幅度差)也越大, 表现出明显的假高阻薄层特征。在层界面处阵列侧向测井仪器的屏流比最大, 而主电极流出的电流不变, 导致在层界面处仪器的聚焦能力最强, 监督电极上的电位最大, 会造成电阻率曲线出现极化角现象。当Rt/Rs小于2时, 阵列侧向测井曲线较为平缓, 几乎不表现出极化角特征, 不需要进行极化角校正; 当Rt/Rs大于4时, 阵列侧向测井曲线形态畸变严重, 层界面附近电阻率严重偏离原状地层电阻率, 且Rt和Rs差别越大偏离的程度越大, 此时应对围岩电阻率造成的电阻率曲线形态畸变进行校正。当围岩为高阻(Rt/Rs小于1)时, 相同电阻率对比度下的模拟结果显示极化角现象基本消失, 说明阵列侧向测井仪器对低电阻率邻层比较敏感, 而对高电阻率邻层不敏感。
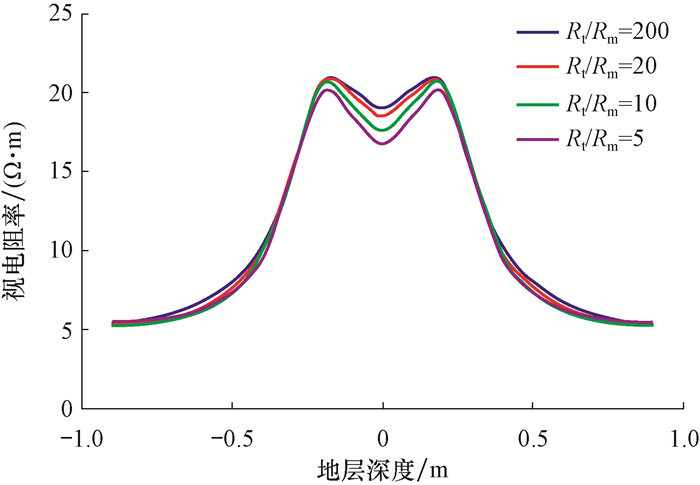
3.2 钻井液电阻率在Rs=5 Ω·m, Rt=20 Ω·m, r=0.203 4 m和H=1.00 m的条件下, 分别模拟阵列侧向测井仪器Rt/Rm为200, 20, 10和5时阵列侧向测井曲线极化角的响应特征。以模式1为例进行分析, 模拟结果见图 5。
|
| 图 5 钻井液电阻率对阵列侧向测井曲线极化角的影响 Fig.5 Effect of resistivity of drilling fluid on the polarizing angle of array laterolog curve |
由图 5可知, Rt/Rm发生变化时, 极化角处的各视电阻率曲线出现一定程度的分离, 且Rm越小极化角峰值越大, 这是因为Rm越小导电能力越强, 测井仪器发出的电流就更多地进入目的层, 导致视电阻率更大的缘故, 但极化角幅度差并不明显, 这说明Rm对阵列侧向测井曲线极化角幅值影响不大, 也说明Rm主要影响极化角的形态, Rm越大则极化角越尖锐。
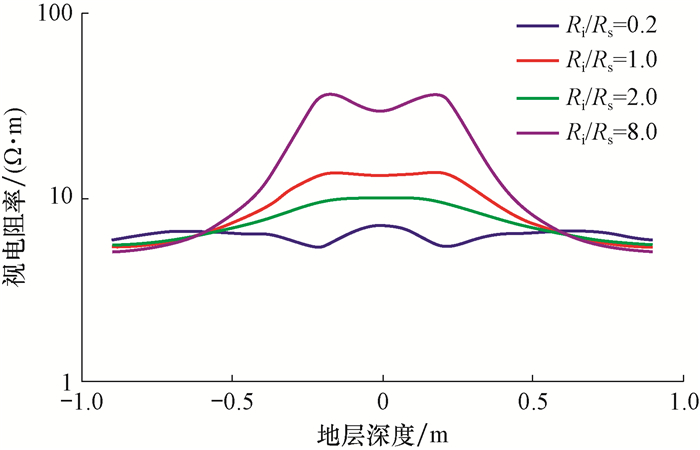
3.3 钻井液侵入带特性在Rs=5 Ω·m, Rt=20 Ω·m, r=0.203 4 m和H=1.00 m的条件下, 以模式1为例, 模拟当ri=0.30 m、Ri变化时阵列侧向测井曲线极化角的响应特征, 结果见图 6; 再在Rt/Ri为2.0和0.5情况下, 分别模拟ri对阵列侧向测井曲线极化角特性的影响, 结果见图 7。
|
| 图 6 侵入带电阻率对阵列侧向测井曲线极化角的影响 Fig.6 Effect of resistivity of invasion zone on the polarizing angle of array laterolog curve |

|
| 图 7 侵入半径对阵列侧向测井曲线极化角的影响 Fig.7 Effect of invasion radius on the polarizing angle of array laterolog curve |
由图 6可知, Ri对阵列侧向测井曲线极化角影响较大。当Ri小于Rs时, 会出现反冲极化角, 类似于地层模型为低阻目的层、高阻邻层时的阵列侧向测井曲线极化角特征; 当Ri等于Rs时, 极化角消失; 当Ri大于Rs时, 极化角表现出与高阻目的层、低阻邻层情况下相似的特征。
由图 7可知, 钻井液侵入为低阻侵入时(Rt/Ri大于1), 随着侵入深度增加, 极化角幅值减小明显, 同时极化角变得越来越平缓; 当钻井液侵入为高阻侵入时(Rt/Ri小于1), 随着侵入深度增加, 极化角幅值越来越大, 同时极化角越来越尖锐。侵入带电阻率不同, 侵入半径对极化角的影响程度也不同, 一般来说, 高阻目的层、高阻侵入条件下的极化角更为明显。
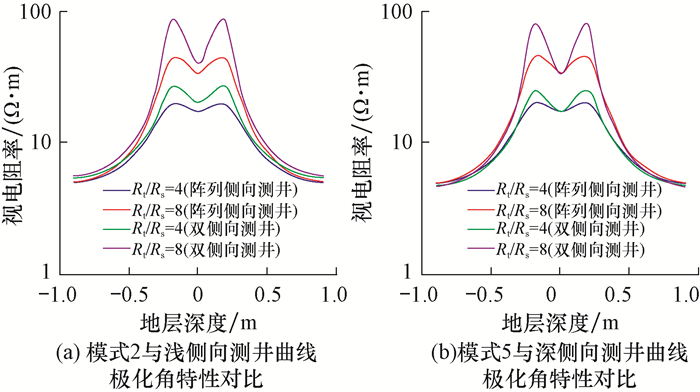
3.4 测井仪器特性在Rs=5 Ω·m, r=0.203 4 m, Rm=1 Ω·m和H=1.00 m的条件下, 分别模拟阵列侧向测井仪器、双侧向测井仪器在相同目的层电阻率背景下测井曲线极化角的响应特征。根据已有文献[12-14], 阵列侧向测井模式2、模式5与浅侧向测井、深侧向测井探测深度相差不大, 故分别选取模式2、模式5与浅侧向测井、深侧向测井进行对比分析, 模拟结果见图 8。
|
| 图 8 测井仪器特性对阵列侧向测井曲线极化角的影响 Fig.8 Effect of instrument characteristics on the polarizing angle of array laterolog curve |
理论上讲, 无论是双侧向测井还是阵列侧向测井, 其视电阻率值在地层厚度大于仪器纵向分辨率的情况下均应接近于原状地层电阻率。由图 8(b)可知, 模式5与深侧向测井是满足此规律的, 但图 8(a)中模式2与浅侧向测井视电阻率在地层中部明显分离, 这是由浅侧向测井的格罗宁根效应[15]造成的。对比阵列侧向测井模式2与模式5的极化角特性以及浅侧向测井与深侧向测井的极化角特性, 发现同一种仪器不同探测深度的视电阻率曲线极化角不论是形态还是幅值均高度相似, 故可知仪器探测深度对侧向测井极化角特性的影响可以忽略不计。模拟采用的阵列侧向测井仪器的纵向分辨率为0.30 m, 双侧向测井仪器的纵向分辨率为0.80 m。由图 8可知, 在其他地层不变的条件下, 仪器纵向分辨率越高极化角现象越不明显。
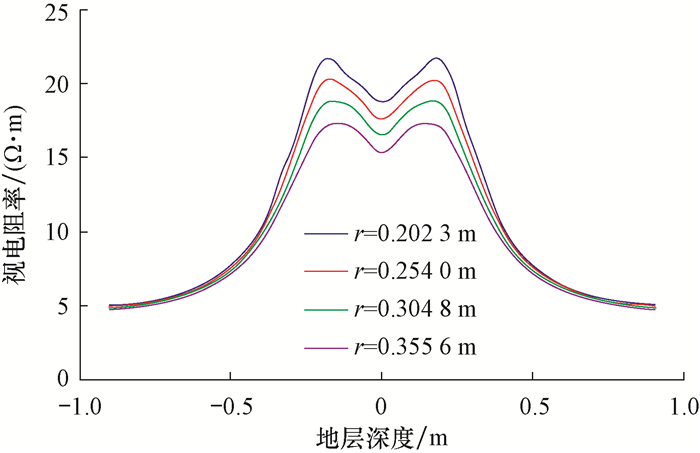
3.5 井径在Rt=20 Ω·m, Rs=5 Ω·m, H=1.00 m和Rm=1 Ω·m的条件下, 分别模拟r为0.202 3, 0.254 0, 0.304 8和0.355 6 m时阵列侧向测井曲线极化角的响应特征。由于模式1至模式5极化角特性受井径影响的规律基本一致, 故以模式5为例进行分析, 模拟结果见图 9。
|
| 图 9 井径对阵列侧向测井曲线极化角的影响 Fig.9 Effect of well diameter on the polarizing angle of array laterolog curve |
由图 9可知, 井径对阵列侧向测井曲线极化角的形态及幅值均有一定影响。随着井径增大, 层界面处的极化角幅值迅速减小, 同时形态变得更加平缓, 即井径越大极化角现象越不明显, 这是由于井径越大, 流入井眼的电流越大, 而流入围岩的电流越少, 导致测井仪器在层界面处的屏流比减小, 故极化角变得越来越不明显。
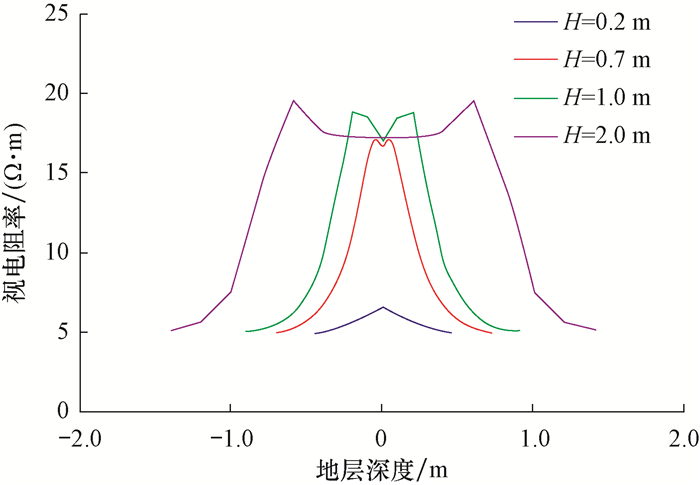
3.6 层厚在Rt=20 Ω·m, Rs=5 Ω·m, Rm=1 Ω·m和r=0.203 4 m的条件下, 分别模拟分析了H为0.20, 0.70, 1.00和2.00 m时阵列侧向测井曲线极化角的响应特征。由于模式1至模式5极化角特性受层厚影响的规律基本一致, 故以模式1为例进行分析, 模拟结果见图 10。
|
| 图 10 层厚对阵列侧向测井曲线极化角的影响 Fig.10 Effect of layer thickness on the polarizing angle of array laterolog curve |
由图 10可知, 层厚对阵列侧向测井曲线的极化角特性影响较为明显。随着层厚增大, 极化角的幅值变得越来越大, 这是由于层厚越大, 流入目的层的电流越多, 导致层界面处屏流比进一步变大的缘故。目的层厚度越小, 极化角越尖锐。目的层厚度越大, 极化角越向两边偏移, 两极化角之间平台区域越大, 即反映储层真实信息的电阻率平台区间越长, 越有利于准确求取储层真实的电阻率。当目的层厚度小于仪器纵向分辨率(0.30 m)时, 极化角现象消失。
3.7 井斜角在Rt=20 Ω·m, r=0.203 4 m, H=1.00 m, Rs=5 Ω·m和Rm=1 Ω·m的条件下, 分别模拟分析了井斜角θ为0°, 15°, 30°, 45°, 60°, 75°和90°时阵列侧向测井曲线极化角的响应特征。由于模式1至模式5中极化角特性受井斜角影响的规律基本一致, 故以模式5为例进行分析, 模拟结果见图 11。

|
| 图 11 井斜角对阵列侧向测井曲线极化角的影响 Fig.11 Effect of well deviation on polarizing angle of array laterolog curve |
由图 11可知, 阵列侧向测井曲线极化角幅值随井斜角增大而减小, 且变得越来越平缓。对于模式5而言, 当井斜角小于15°时, 随着井斜角增大极化角特性基本无改变; 当井斜角大于15°时, 随着井斜角增大极化角变得越来越平缓, 同时幅值也变得越来越小; 当井斜角大于60°时, 模式5的极化角现象基本消失, 这是由于随着井斜角增大, 越来越多的电流直接进入围岩, 流入目的层的电流减少导致仪器屏流比减小的缘故。
4 结论1) 围岩电阻率变化对阵列侧向测井曲线极化角特性的影响最大, 尤其是低阻围岩。当目的层电阻率与低阻围岩电阻率的比值大于4时, 极化角幅值急剧增大, 对视电阻率曲线相态造成严重影响, 在进行极化角校正时围岩是一个不可忽略的主控因素。
2) 钻井液侵入带特性对极化角特性影响复杂, 需综合考虑侵入带电阻率与侵入半径的影响。一般来说, 高阻目的层、高阻侵入情况下的极化角较为明显, 需进行相关极化角校正处理。
3) 阵列侧向测井仪器纵向分辨率越高, 极化角现象越不明显, 故当常规侧向仪器极化角现象过于明显、严重影响到测井解释的情况下, 可考虑采用高分辨率阵列侧向类测井仪器。
4) 钻井液电阻率变化主要影响极化角形态, 对其幅值影响不大; 随着层厚增大, 极化角幅值变大, 但极化角变得更加平缓; 井径越大, 极化角幅值越小, 形态越平缓; 井斜角越大, 极化角越不明显, 井斜角大于60°时, 极化角基本消失。
| [1] |
范晓敏.
双侧向测井曲线形状与地层侵入关系研究[J]. 地球物理学进展, 2007, 22(1): 142–146.
FAN Xiaomin. Investigation on the relation between form of laterologs and invasion state of reservoir[J]. Progress in Geophysics, 2007, 22(1): 142–146. |
| [2] |
范宜仁, 巫振观, 王磊, 等.
大斜度井各向异性地层双感应测井响应特征研究[J]. 测井技术, 2016, 40(3): 262–269, 275.
FAN Yiren, WU Zhenguan, WANG Lei, et al. Response characteristics of dual induction logging in anisotropic formation and high deviated wells[J]. Well Logging Technology, 2016, 40(3): 262–269, 275. |
| [3] | ANDERSON B I, BANNER S, LULING M G, et al. Response of 2-MHz LWD resistivity and wireline induction tools in dipping beds and laminated formations[R]. SPWLA-1990-A, 1990. |
| [4] |
杨震, 范宜仁, 文艺, 等.
三维频率域随钻电磁波测井数值模拟[J]. 地球物理学进展, 2009, 24(5): 1833–1838.
YANG Zhen, FAN Yiren, WEN Yi, et al. Three-dimensional numerical simulation of electromagnetic logging-while-drilling tool response in frequency domain[J]. Progress in Geophysics, 2009, 24(5): 1833–1838. |
| [5] |
朱庚雪, 刘得军, 张颖颖, 等.
基于hp-FEM的随钻电磁波测井仪器响应正演分析[J]. 石油钻探技术, 2015, 43(2): 63–70.
ZHU Gengxue, LIU Dejun, ZHANG Yingying, et al. Forward modeling of responses of an ELWD tool based on hp-FEM[J]. Petroleum Drilling Techniques, 2015, 43(2): 63–70. |
| [6] |
李勇华, 杨锦舟, 杨震, 等.
随钻电阻率地层边界响应特征分析及应用[J]. 石油钻探技术, 2016, 44(6): 111–116.
LI Yonghua, YANG Jinzhou, YANG Zhen, et al. The analysis and application of formation interface response characteristics of the resistivity LWD tool[J]. Petroleum Drilling Techniques, 2016, 44(6): 111–116. |
| [7] | WANG T L, SIGNORELLI J. Finite-difference modeling of electromagnetic tool response for logging while drilling[J]. Geophysics, 2004, 69(1): 152–160. DOI:10.1190/1.1649383 |
| [8] |
刘迪仁, 万文春, 夏培, 等.
不同井眼条件下的水平井双侧向测井响应[J]. 物探与化探, 2012, 36(3): 422–425.
LIU Diren, WAN Wenchun, XIA Pei, et al. The response of dual laterolog to different borehole conditions in the horizontal well[J]. Geophysical & Geochemical Exploration, 2012, 36(3): 422–425. DOI:10.11720/wtyht.2012.3.19 |
| [9] |
张庚骥.
电阻率测井响应的积分方程解法[J]. 地球物理学报, 1985, 28(5): 519–525.
ZHANG Gengji. The response of resistivity logging obtained by solving integral equations[J]. Acta Geophysica Sinica, 1985, 28(5): 519–525. |
| [10] |
夏培, 刘迪仁, 万文春, 等.
水平井各向异性地层双侧向测井响应数值模拟[J]. 石油天然气学报, 2011, 33(8): 104–106.
XIA Pei, LIU Diren, WAN Wenchun, et al. Numerical simulation of dual laterolog response in anisotropic formation of horizontal wells[J]. Journal of Oil and Gas Technology, 2011, 33(8): 104–106. |
| [11] |
陈亮. 斜井、水平井双侧向测井响应三维有限元数值分析[D]. 杭州: 浙江大学, 2008.
CHEN Liang. Three dimensional finite element numerical analysis of dual laterolog response in inclined shaft and horizontal well[D]. Hangzhou: Zhejiang University, 2008. |
| [12] |
仵杰, 谢尉尉, 解茜草, 等.
阵列侧向测井仪器的正演响应分析[J]. 西安石油大学学报(自然科学版), 2008, 23(1): 73–76, 80.
WU Jie, XIE Weiwei, XIE Xicao, et al. Forward response analysis of array lateral logging tool[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2008, 23(1): 73–76, 80. |
| [13] |
刘振华, 胡启.
阵列侧向测井响应的计算及其特征[J]. 西安石油学院学报(自然科学版), 2002, 17(1): 53–57.
LIU Zhenhua, HU Qi. Calculation and characteristics of array laterlog responses[J]. Journal of Xi'an Petroleum Institute(Natural Science Edition), 2002, 17(1): 53–57. |
| [14] |
杨韡.
阵列侧向测井的正反演[J]. 勘探地球物理进展, 2003, 26(4): 305–308.
YANG Wei. Forward and backward in array lateral logging[J]. Progress in Exploration Geophysics, 2003, 26(4): 305–308. |
| [15] |
柳杰. 电流势法在直流电测井模拟中的应用[D]. 杭州: 浙江大学, 2015.
LIU Jie. Application of current potential method in DC electrical logging[D]. Hangzhou: Zhejiang University, 2015. |



