2. 长江大学地球物理与石油资源学院, 湖北武汉 430100;
3. 中国石油集团西部钻探工程有限公司测井公司, 新疆克拉玛依 834000
2. Geophysics and Oil Resource Institute, Yangtze University, Wuhan, Hubei, 430100, China;
3. Well Logging Company, CNPC Xibu Drilling Engineering Company Limited, Karamay, Xinjiang, 834000, China
随着油气勘探开发逐渐由常规油气藏转向非常规油气藏,储层裂缝的研究越发重要。裂缝不仅可以作为油气储集空间,也是油气运移的重要通道,所以裂缝识别是裂缝性储层研究的重要组成部分[1]。测井和地震是油气勘探中的2种重要手段[2]:测井资料能够刻画井壁地层及其岩性的发育情况,但是测井成本太高及反映信息的范围不足限制了其适用性[3-5]。利用测井资料识别裂缝以人工识别为主,主要依靠经验分析,识别标准也各不相同,受技术人员对地质、测井、地震知识理解程度的限制,主观因素影响较大[6], 导致裂缝识别效率低;地震裂缝预测识别技术发展迅速[7-11],与测井资料识别裂缝相比,地震资料分辨率低,但地震波覆盖范围广、传播深度大,解决了测井预测范围小的问题。将地震预测技术和测井资料识别相互结合,基于各向异性理论预测裂缝,既能刻画裂缝发育程度,又能表征裂缝发育走向,李军[12]、Hampson[13]和Leiphart等人[14]结合2种方法进行了裂缝预测,取得较好的应用效果。
测井方法和地震检测虽然在各自领域均表现出良好的应用效果,但无法对裂缝反演强度进行定量化研究[15]。笔者根据裂缝的常规测井曲线的响应特征,提出了基于粗糙集的测井裂缝识别与地震裂缝预测相融合的碳酸盐岩储层裂缝预测方法。实例应用表明,测井裂缝识别与成像测井结果吻合度高,通过测井裂缝与叠前地震各向异性结果交互标定,可以有效识别碳酸盐岩储层裂缝的发育强度,对于指导相近碳酸盐岩储层裂缝预测具有一定的借鉴意义。
1 预测方法的原理 1.1 基于粗糙集的测井裂缝发育评价裂缝在常规测井曲线上的响应特征是测井裂缝识别的基础[16-17]。裂缝测井响应特征有助于定性判断裂缝发育情况,要想达到定量识别裂缝的目的,须将其转化为定量指标,从而实现对裂缝定量直观的表征[18-19]。
粗糙集只依赖于数据本身,从不完整的数据集中发现模式和规律,不需要样本之外的经验或者附加信息,能避免人为选择决策机制过程中的主观性,仅根据所观测数据删除冗余信息,分析不完整知识的程度,生成分类或决策规则,是一种处理模糊和不确定性知识的数学工具[20-21],这为裂缝定量化识别提供了方法支撑。
粗糙集理论中,“知识”可以被看作一种分类能力,可以理解为对数据的划分。用集合的观念表达就是:使用等价关系集R对离散表示的空间U进行划分,知识就是R对U的划分结果,由此在U及R的意义下,知识库K可以定义为:属于R中的所有可能关系对U的划分,记作:
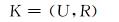
|
(1) |
假设知识系统S=(U, A, V, f),其中,U是对象的非空有限集合,称为论域对象空间;A是属性集合,V是属性值集合,f为信息函数,则
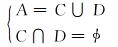
|
(2) |
式中:子集C为条件属性集, 子集D为决策属性集。
具有条件属性和决策属性的知识表达系统称为决策表,即称T=(U, R, C, D)为决策表。假定:
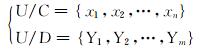
|
(3) |
决策属性集D依赖于条件属性集C的依赖度k为:
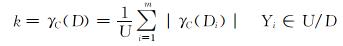
|
(4) |
式中:k为决策属性集D依赖于条件属性集C的依赖度。
k=1时,D完全依赖于C;0 < k < 1时,D部分依赖于C;k=0时,D完全独立于C。
在决策表中,不同的属性可能具有不同的重要性。为了找出某些属性的重要性,从决策表中去掉一些属性,考察没有该属性后的分类变化情况。若去掉该属性后,相应的分类变化较大,说明该属性的强度大,即重要性高;反之,说明该属性的强度小,即重要性低。定义条件属性Ci关于决策属性集D的重要程度σCD(Ci)为:
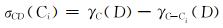
|
(5) |
其中
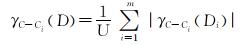
|
(6) |
式中:γC-Ci(D)为决策属性集D对条件属性Ci的依赖度。
σCD(Ci)越大,说明属性Ci在整个属性集中的重要性越高。
识别指标权系数是建立裂缝发育强度识别模型的关键,计算流程如下:
1) 利用式(4) 计算最简决策表中决策属性集对条件属性集的依赖度γC(D);
2) 对每个识别指标Ci,根据式(6) 计算决策属性集D对条件属性Ci的依赖度γC-Ci(D);
3) 根据式(5) 计算第i种识别指标在指标集合中的重要性σCD(Ci);
4) 计算第i种评判指标的权系数αi, 公式为:
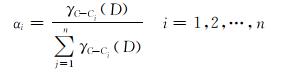
|
(7) |
测井裂缝识别指标包括曲线变化率、岩石孔隙结构指数、地层因素比值、饱和度比、骨架指数和三孔隙度比,以上指标作为条件属性集,以测井裂缝识别结果的不发育、低密度微裂缝、中密度裂缝和高密度裂缝为决策属性集,通过建立识别量版,实现测井裂缝的定量识别,避免结果受人为划分的主观及经验因素的干扰,主要步骤如下:
1) 根据地质特征、岩电对比资料确定研究区域特定裂缝所对应的测井曲线响应特征;
2) 利用测井裂缝识别指标及地震裂缝预测结果离散化区间构建模型的条件属性集和决策属性集;
3) 利用样本构建模型的待识别裂缝发育类别;
4) 利用基于粗糙集理论的权系数,得出待估样本的识别结果。
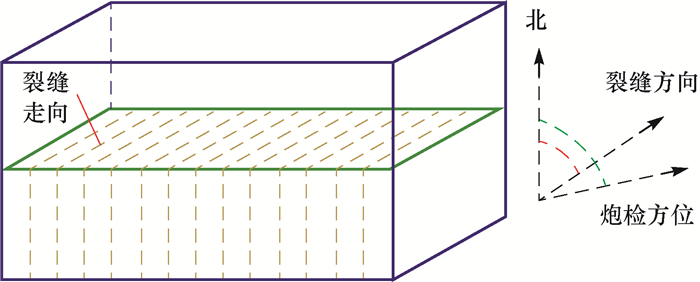
1.2 叠前地震方位各向异性裂缝预测Andreas Ruger[22]对Christoffel方程进行了一系列简化,提出了Ruger近似公式,并通过比较分析计算的理论模型反射系数发现,Ruger近似公式在弱各向异性的垂直定向排列裂缝介质(HTI介质)中具有很好的适用性,利用其进行AVO梯度反演可计算HTI介质中的裂缝参数。地震波在裂缝介质中传播的反射系数随方位变化的情况如图 1和图 2所示。
|
| 图 1 地震反射振幅随方位的变化 Fig.1 Changes in amplitudes of seismic reflection with changes in azimuth |
|
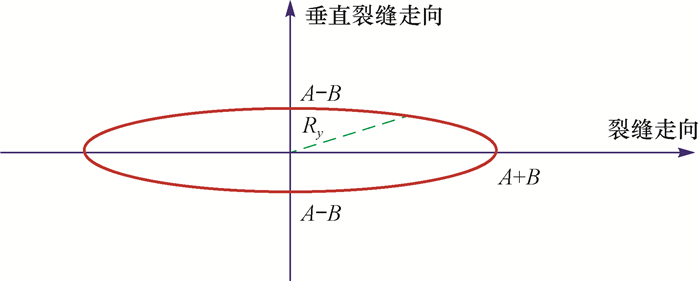
| 图 2 AVAZ拟合椭圆图 Fig.2 Ellipse for AVAZ fitting |
纵波在裂缝介质传播时,当偏移距一定时纵波的反射振幅随方位变化的关系为[23]:
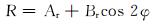
|
(8) |
式中:R为反射振幅;φ为观测方向与裂缝走向的夹角,(°);Ar为均匀介质下的振幅;Br为裂缝引起的振幅变化调制因子,即Br是在固定偏移距下随观测方位的变化而引起的振幅变化量,Ar和Br之间的相对变化能够反映裂缝的发育情况和走向。
前人对裂缝介质的大量研究成果表明,纵波在裂缝介质传播过程中,纵波的反射振幅与观测方位的关系可以近似拟合成椭圆图形式,如图 2所示。当平行裂缝走向观测时,采集的纵波振幅最强,其振幅值为(A+B);当垂直裂缝走向观测时,采集的纵波振幅最弱,其振幅值为(A-B)。构建比值关系(A+B)/(A-B),用来表征地下裂缝的发育程度。
因此,利用3个方位角即可实现对裂缝密度和发育方位的定量预测。假设每个共中心道集在相同固定偏移距上具有3个方位的观测资料R(φ)、R(φ+α)和R(φ+β), 其中φ为首个观测方位与裂缝发育走向之间的夹角, α和β分别为第二个和第三个方位道集与首个道集之间的角度,可以通过已知的采集观测系统计算获得α和β,联立方程组求解Ar和Br:
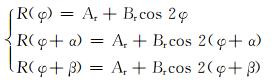
|
(9) |
获得Ar, Br及裂缝方位的对应数值,最终实现对裂缝密度和走向的刻画。虽然3个方位的地震数据可以满足求解式(9) 的条件,但是方位信息量不够,对裂缝的刻画必然会不充分,导致求得的结果随机性很强,容易受到噪音干扰。
为了提高预测结果的稳定性,更真实地反映出地下裂缝信息, 通常采用多个方位信息的组合, 根据式(9) 构建超定方程组,可以采用最小二乘反演方法求解超定方程组,得到A、B及裂缝方位。
针对N(N>3) 个不同方位角的反射振幅,可以建立超定方程:
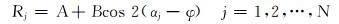
|
(10) |
式中:Rj为反射系数; αj为观测方位角, (°)。
令fj(X)=Rj-A-Bcos 2(αj-φ),其中X=[A, B, φ]T,则可以建立目标函数:
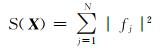
|
(11) |
函数fj是关于A, B和φ的多元函数,对其进行一阶泰勒展开,可得:
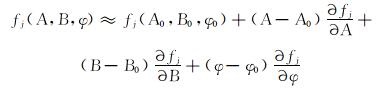
|
(12) |
将式(12) 代入式(11),可得:
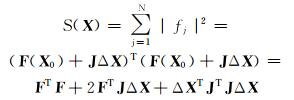
|
(13) |
式中:J为雅克比矩阵。
给出初始值X0,目标函数式是关于增量ΔX的函数,要使目标函数最小,可有:
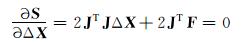
|
(14) |
对式(14) 进行形式变换,可得:
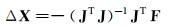
|
(15) |
则最小二乘解的迭代形式为:
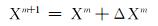
|
(16) |
通过上述算法,给出初始值,即可求取A、B和φ。首先利用宽方位观测系统进行资料采集,再进行分方位处理,提取叠前地震方位的地震数据,研究P波振幅随方位角的变化与裂缝之间的关系,根据以上基本算法,通过裂缝介质中纵波表现出的方位各向异性特征,就可以判别油气储层中的裂缝方位和裂缝发育程度。
1.3 测井与地震数据的尺度匹配测井数据的采样间隔通常为0.125 m,地震采样间隔为2 ms,地震数据与测井数据的频宽及频率成分有很大的不同,导致进行深时转换时,测井数据与地震数据存在尺度不匹配的问题,因此采用中值滤波法实现二者的尺度匹配。中值滤波法是一种非线性平滑技术,它把时窗内的值按大小排序,然后将中间值重新置于窗的中心点,并通过时窗的滑动来实现这一过程,可以保持信号的边缘不被恶化。中值滤波法能消除声波测井数据中的异常峰值,同时,还能消除高频成分的影响。
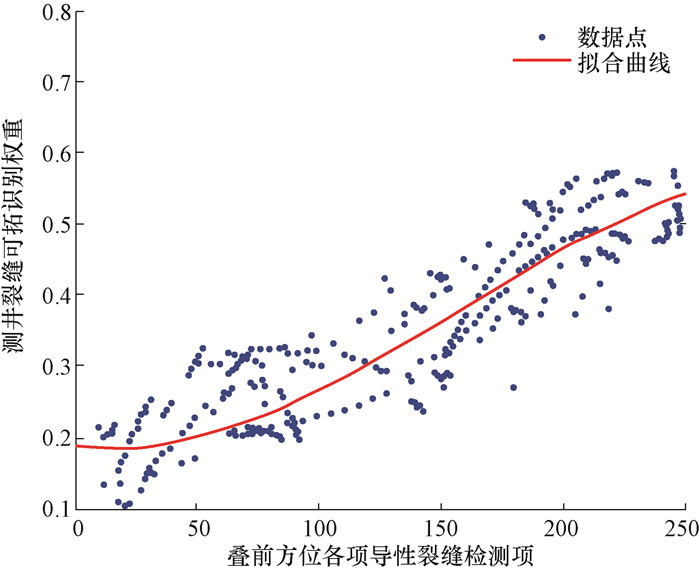
对一个给定的序列{Xi}(i=1, 2, …, n),其中值滤波过程如下:
1) 选择时窗的大小,也就是滤波点数m(m≤n);
2) 从第一个数据点开始,取m个数据,比较其值的大小,把m个数据的中位数{Yi}作为中值滤波的输出结果;
3) 向前移动一个点,并重复步骤2),开始下一个点计算,直到完成所有点计算。
需要说明的是,当m为奇数时,Yi的值取X(i-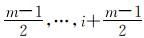
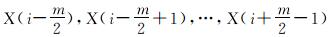
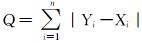
采用中值滤波有效消除测井高频采样的干扰,实现与地震资料频率相匹配,然后将测井裂缝识别结果与叠前地震裂缝强度的曲线进行多项式拟合,得到裂缝发育分类与裂缝密度的对应关系,就可以定量刻画地震裂缝发育情况,实现测井地震信息融合的裂缝综合识别。
2 应用实例X区块位于中东某国的扎格罗斯褶皱带,构造主要为北西南东向的背斜,具备典型的前陆盆地结构特征。研究区目的层为白垩系,包含Shiranish, Kometan及Qamchuqa组3个层段。目的层段位于背斜构造区域,由于挤压褶皱作用导致目的层段Shiranish段以下的层段(Kometan段和Qamchuqa段)结构破碎,裂缝发育且分布复杂;同时,工区主要发育泥灰岩、灰岩和白云岩。目的层白垩系平均孔隙度为20%,渗透率为100~525 mD,为高孔中高渗海相沉积环境。
该研究区具有较好的叠后地震和方位地震处理成果资料,测井资料也相对齐全,既有常规测井资料,部分井又有成像测井资料,为后续对该区碳酸盐岩裂缝性储层从叠后地震、叠前地震、常规测井及成像测井多重手段多个角度的全面研究提供了很好的基础。针对工区的特点及现有的资料,利用测井-地震信息的碳酸盐岩储层裂缝预测开展研究区的裂缝检测,验证相关流程的合理性及可行性。
2.1 基于测井资料的裂缝识别根据测井参数对裂缝的响应特征及敏感性,对比优选出能够反映裂缝发育程度的地质及测井参数,分别是声波时差变化率、岩石孔隙结构指数、地层因素比值、饱和度比、骨架指数和三孔隙度比值[24],决策属性1—4分别代表不发育、低密度裂缝、中密度裂缝和高密度裂缝。
根据裂缝在常规测井曲线上的响应特征,利用常规测井获得的测井曲线、钻井、录井及取心等资料,建立关系数据模型、进行属性特征化和建立决策表,通过属性约减计算出定量衡量裂缝发育程度的各指标权重,实现对裂缝常规测井的定量描述。以下为实际工区的具体实现过程。
选取研究区较为典型的30口井的成像测井结果及常规测井曲线作为样本,对样本进行量化处理后得到初始决策表,通过相容性检查,完成属性约减。根据式(6) 计算声波时差变化率、岩石孔隙结构指数、地层因素比值、饱和度比、骨架指数和三孔隙度比值等指标对应的γC-Ci(D)值,分别为0.311,0.356,0.289,0.467,0.333和0.445;根据式(5) 计算得到各指标的重要性σCD(Ci),分别为0.689,0.644,0.711,0.533,0.667和0.555;最后根据式(7) 计算得到各指标的权重系数,分别为0.185,0.169,0.191,0.145,0.179和0.151。
选取工区35口井进行裂缝发育识别,识别结果的吻合率达到85%,说明基于粗糙集的裂缝发育可拓识别方法可行,部分井段裂缝发育识别结果见表 1,其中各指标进行了标准化换算,以统一计算尺度。从表 1可以看出,识别结果基本符合实际测井裂缝发育检测结果。
| 样本号 | 声波时差变化率 | 孔隙结构指数 | 地层因素比值 | 饱和度比 | 骨架指数 | 三孔隙度比值 | 基于粗糙集识别结果 | 实测结果 |
| 1 | 21.21 | 13.29 | 2.32 | 1.04 | 0.17 | 0.25 | 1 | 1 |
| 2 | 15.16 | 24.67 | 5.43 | 1.64 | 0.32 | 0.19 | 2 | 2 |
| 3 | 10.42 | 12.73 | 1.02 | 1.52 | 0.17 | 0.22 | 3 | 3 |
| 4 | 16.31 | 11.63 | 1.09 | 1.38 | 0.08 | 0.19 | 4 | 4 |
| 5 | 7.01 | 8.43 | 0.41 | 0.39 | 0.18 | 0.17 | 4 | 4 |
| 6 | 38.98 | 18.01 | 2.21 | 0.83 | 0.09 | 0.14 | 3 | 4 |
在该区测井裂缝识别研究中,利用常规测井裂缝预测方法对T4井、T8井和T9井等多口井的中生界井段进行了裂缝预测。T4井裂缝识别与测井解释对比结果如图 3所示。从图 3可以看出,岩性与裂缝发育强度关联密切,白云岩集中区的裂缝发育强度总体高,灰岩井段的裂缝发育相对弱,与岩石物理统计信息相吻合,说明白云岩是裂缝发育的有利岩性。

|
| 图 3 T4井裂缝识别与测井裂缝解释对比 Fig.3 Fractures identified and fracture interpretation based on logging data in Well T4 |
成像测井不仅能直观刻画描述复杂孔隙结构(裂缝、溶孔、溶洞、层理和井壁坍塌)的实际特征,还能进行图像处理解释出裂缝参数,所以,可以利用该区已有成像测井解释的裂缝密度FVDC与常规测井基于粗糙集可拓识别结果进行对比。
图 4为T8井某井段裂缝识别与岩性解释及成像测井裂缝密度对比结果。从图 4可以看出,成像测井解释结果与测井识别裂缝结果基本吻合,在成像测井解释裂缝密度高的井段,常规测井识别的裂缝发育程度也比较强。该结果一方面验证了常规测井裂缝可拓识别的可靠性;另一方面说明,当成像测井资料缺乏时,可以考虑采用利用常规测井资料基于粗糙集的可拓识别方法定量预测裂缝。对图 4所示T8井某井段裂缝可拓识别结果与岩性柱及成像测井裂缝密度进行对比,同样可以发现,2种识别方式的预测结果具有高度的一致性,进一步确定了常规测井基于粗糙集可拓识别方法的有效性。
|
| 图 4 T8井某井段裂缝识别与岩性解释及成像测井裂缝密度解释对比 Fig.4 Fracture identification, lithologic interpretation and fracture density determined by using image logging data in Well T8 |
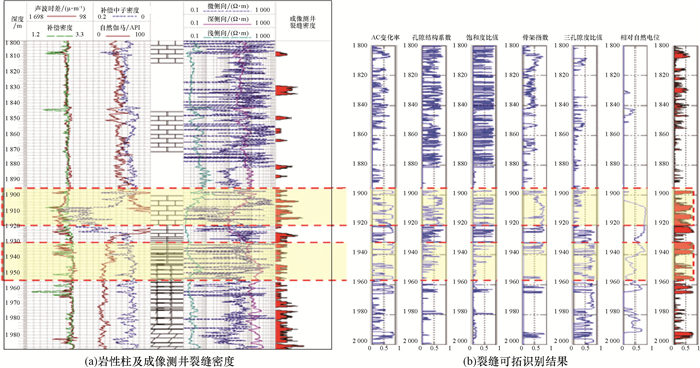
基于振幅的方位各向异性裂缝预测技术不仅能够有效刻画大尺度断层特征,也能够有效分辨小尺度裂缝发育信息。图 5所示为主要试井解释渗透率与裂缝预测结果的层段对比结果(图中纵向蓝色柱表示试油井段;底部横向彩色柱表示“裂缝发育密度”,表示裂缝的发育程度)。从图 5可以看出,纵波方位各向异性预测结果能够有效识别剖面上的同相轴大的错断及微弱的不连续性,很好地说明该方法识别裂缝的有效性。试井结果表明,总体来说,对应井段渗透率随试井层段埋深增加而增大;裂缝密度与试井解释的渗透率成正相关趋势。已钻井目的层段试井解释的渗透率与裂缝预测结果吻合率的统计结果表明,测井解释分层平均吻合率可达到80%左右。试井层段经酸化改造后,地层孔隙大小发生改变,会出现试井解释所得的渗透率与地震预测裂缝密度趋势不吻合的情况。
|
| 图 5 联井裂缝密度与试井渗透率剖面对比 Fig.5 Well-tie fracture density contrasted and permeability profile of the tested interval |
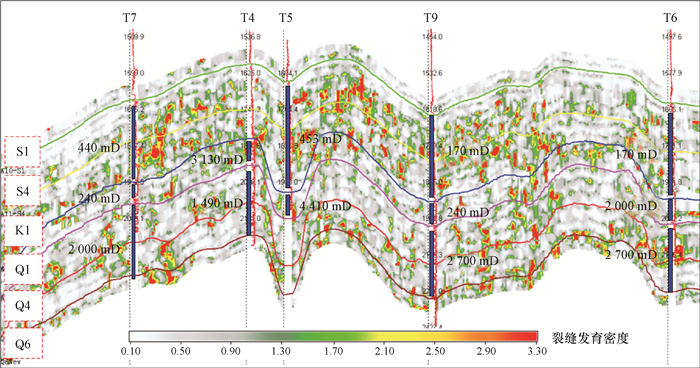
根据三阶多项式最小误差原则,对测井裂缝可拓识别结果与叠前地震裂缝预测结果(见图 6)进行拟合,可得:
|
| 图 6 测井裂缝可拓识别权重与叠前方位各向异性检测拟合 Fig.6 Well logging extension identification weight and pre-stack azimuthal anisotropy fitting curve |
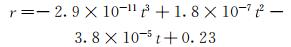
|
(17) |
式中:r为叠前地震裂缝检测强度;t为测井裂缝可拓识别指标综合权重。
从拟合结果可以看出,叠前裂缝检测结果与测井裂缝识别结果的低频近似,这也符合地震-测井的频率分布规律。
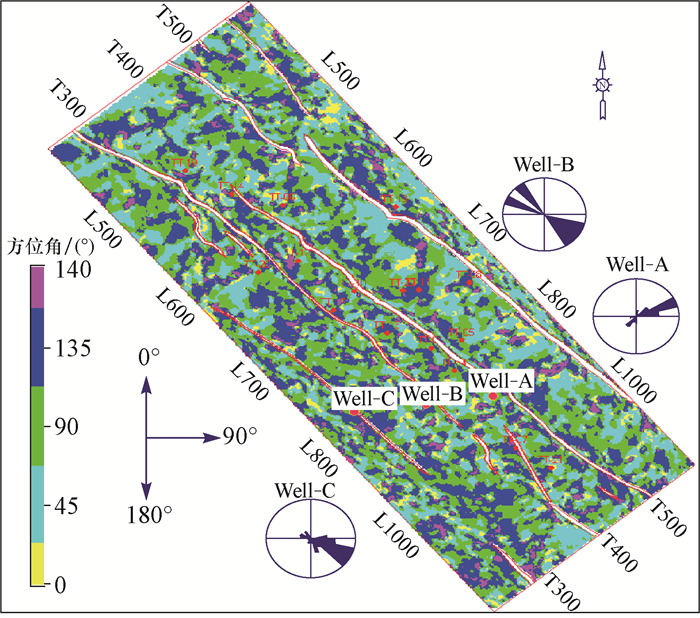
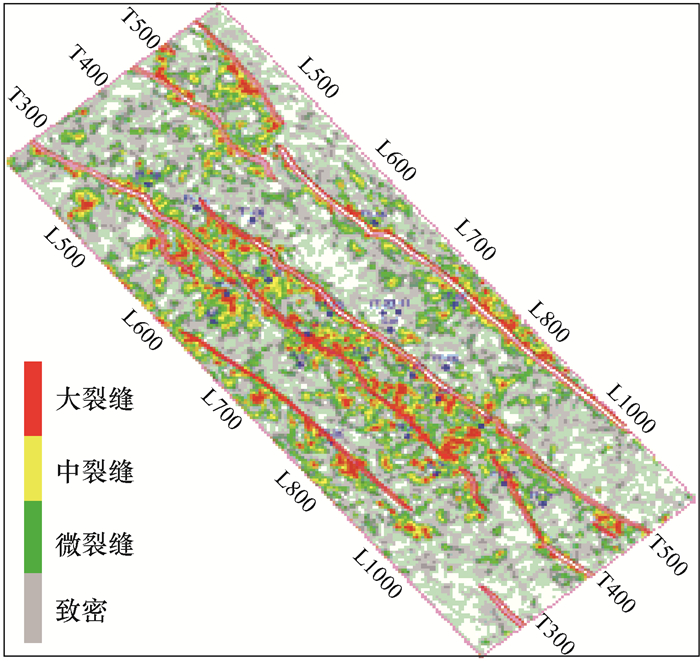
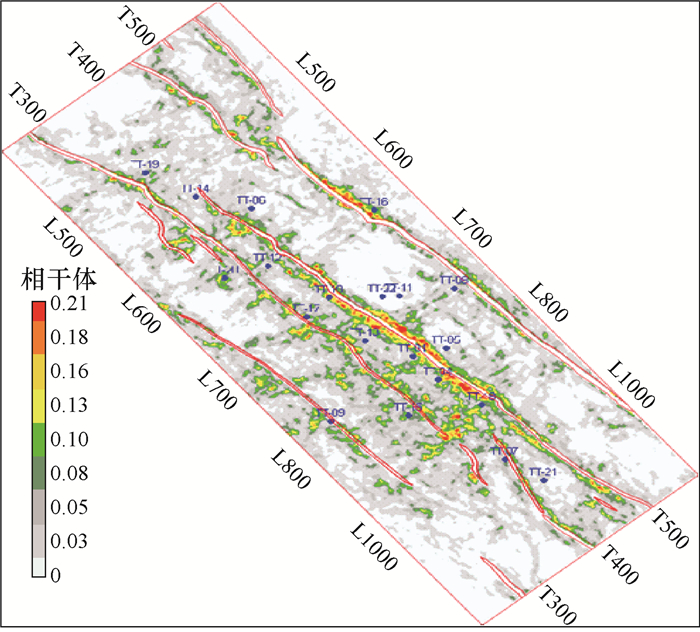
采用中值滤波法实现测井与地震尺度匹配后,利用拟合关系式进行叠前地震方位各向异性检测结果向裂缝发育级别信息的转换及与叠后相干体的对比,结果见图 7、图 8和图 9。从图 7可以看出,工区裂缝发育方位以中等角度为主,与构造密切相关;由于工区构造背斜核部受挤压应力作用,裂缝方位主要表现为垂直和平行构造走向。图 8为裂缝发育强度预测结果,图中的大裂缝、中裂缝、微裂缝和致密分别对应高密度裂缝、中密度裂缝、低密度裂缝和不发育,可以看出裂缝发育程度与构造之间具有一定的正相关性,通过测井-地震综合预测,能够得到定量化的裂缝发育强度及方位信息。叠后相干体能够有效刻画大的断裂构造背景,对断裂轮廓之外的裂缝信息识别能力相对弱;叠前地震方位各向异性裂缝预测利用了地震资料方位和偏移距信息,分辨率更高,对微裂缝等小尺度断裂刻画效果显著。同时,利用测井结果标定地震反演结果,使地震预测结果的物理含义更加明确(见图 9)。
|
| 图 7 裂缝发育方位 Fig.7 Azimuth of fracture development |
|
| 图 8 裂缝发育强度预测平面展布 Fig.8 Plane distribution of fracture development intensities |
|
| 图 9 裂缝叠后相干体 Fig.9 Coherence of post-stack fractures |
1) 根据测井资料及地震信息建立了基于测井-地震信息的碳酸盐岩储层裂缝预测方法,其中基于粗糙集的常规测井识别能够避免人为划分权重,可以实现对测井裂缝发育的高效定量刻画。
2) 叠前地震方位各向异性裂缝预测结果分辨率更高,预测的裂缝信息更加丰富,可用于低密度裂缝的识别。将裂缝评价权系数与缝发育密度建立映射,能够避免单一方法的局限性,提高预测结果的可靠性。
3) 实际工区的裂缝发育识别结果表明,基于测井-地震信息的碳酸盐岩储层裂缝预测方法可以实现对不同裂缝级别的有效预测,同时能够更加直观地刻画裂缝级别和更加精确地认识裂缝发育程度及分布规律,可以为相同或相近类型的碳酸盐岩储层裂缝识别提供一定的参考。
| [1] |
穆龙新, 赵国良.
储层裂缝预测研究[M]. 北京: 石油工业出版社, 2009: 32-70.
MU Longxin, ZHAO Guoliang. Study on reservoir fracture prediction[M]. Beijing: Petroleum Industry Press, 2009: 32-70. |
| [2] |
张军华.
断块、裂缝型油气藏地震精细描述技术[M]. 东营: 中国石油大学出版社, 2012: 28-33.
ZHANG Junhua. Seismic fine description technique for fault block and fractured reservoirs[M]. Dongying: China University of Petroleum Press, 2012: 28-33. |
| [3] |
孙建孟, 刘蓉, 梅基席, 等.
青海柴西地区常规测井裂缝识别方法[J]. 测井技术, 1999, 23(4): 268–272.
SUN Jianmeng, LIU Rong, MEI Jixi, et al. Fracture identification technique by conventional logs from Western Chaidamu Basin, Qinghai Oilfield[J]. Well Logging Technology, 1999, 23(4): 268–272. |
| [4] |
冯翠菊, 闫伟林.
利用常规测井资料识别变质岩储层裂缝的方法探讨[J]. 国外测井技术, 2008, 23(2): 14–16.
FENG Cuiju, YAN Weilin. Discussion on identification of the fractures in metamorphic rock reservoir with conversational logging data[J]. World Well Logging Technology, 2008, 23(2): 14–16. |
| [5] |
龚佳, 秦迎春, 王宁, 等.
综合概率法在白云岩储层裂缝识别中的应用[J]. 内蒙古石油化工, 2011, 21(14): 148–151.
GONG Jia, QIN Yingchun, WANG Ning, et al. The application of the comprehensive probability method identifying the dolomite reservoir fracture[J]. Inner Mongolia Petrochemical Industry, 2011, 21(14): 148–151. DOI:10.3969/j.issn.1006-7981.2011.14.060 |
| [6] |
刘振峰, 曲寿利, 孙建国, 等.
地震裂缝预测技术研究进展[J]. 石油物探, 2012, 51(2): 191–198.
LIU Zhenfeng, QU Shouli, SUN Jianguo, et al. Progress of seismic fracture characterization technology[J]. Geophysical Prospecting for Petroleum, 2012, 51(2): 191–198. |
| [7] |
刘军迎. 裂缝型油气藏叠前地震检测方法技术研究[D]. 成都: 成都理工大学, 2012: 1-22.
LIU Yingjun.Fractured hydrocarbon reservoirs pre-stack seismic detection methods and techniques[D].Chengdu:Chengdu University of Technology, 2012:1-22. http://cdmd.cnki.com.cn/Article/CDMD-10616-1012500832.htm |
| [8] |
何巍巍. 裂缝性储层预测研究: 以川东北嘉陵江组二段储层为例[D]. 北京: 中国地质大学(北京), 2010: 8-22.
HE Weiwei.Research on prediction in fractured reservoir:taking the reservoir of the Jialingjiang No.2 member in Northeastern Sichuan Basin for example[D].Beijing:China University of Geosciences (Beijing), 2010:8-22. http://d.wanfangdata.com.cn/Thesis/Y1782343 |
| [9] |
曲寿利, 季玉新, 王鑫, 等.
全方位P波属性裂缝检测方法[J]. 石油地球物理勘探, 2001, 36(4): 390–397.
QU Shouli, JI Yuxin, WANG Xin, et al. Seismic method for using full-azimuth P-wave attribution to detect fracture[J]. Oil Geophysical Prospecting, 2001, 36(4): 390–397. |
| [10] |
魏建新, 狄帮让.
裂隙密度对纵波传播特性影响的实验观测[J]. 石油地球物理勘探, 2007, 42(5): 554–559.
WEI Jianxin, DI Bangrang. Experimentally surveying influence of fractural density on P-wave propagating characters[J]. Oil Geophysical Prospecting, 2007, 42(5): 554–559. |
| [11] |
魏建新, 狄帮让, 王椿镛.
岩石正交各向异性的实验观测[J]. 地球物理学进展, 2008, 23(2): 343–350.
WEI Jianxin, DI Bangrang, WANG Chunyong. The experimental observation of the rock orthorhombic anisotropy[J]. Progress in Geophysics, 2008, 23(2): 343–350. |
| [12] |
李军, 郝天珧, 赵百民.
地震与测井数据综合预测裂缝发育带[J]. 地球物理学进展, 2006, 21(1): 179–183.
LI Jun, HAO Tianyao, ZHAO Baimin. Synthetic predication of favorable fracture zone from seismic and log data[J]. Progress in Geophysics, 2006, 21(1): 179–183. |
| [13] | HAMPSON D P, SCHUELKE J S, QUIREIN J A. Use of multiattribute transforms to predict log properties from seismic data[J]. Geophysics, 2001, 66(1): 220–236. DOI:10.1190/1.1444899 |
| [14] | LEIPHART D J, HART B S. Comparison of linear regression and a probabilistic neural network to predict porosity from 3-D seismic attributes in Lower Brushy Canyon channeled sandstones, Southeast New Mexico[J]. Geophysics, 2001, 66(5): 1349–1358. DOI:10.1190/1.1487080 |
| [15] |
贾跃玮, 魏水建, 吕林.
应用地震纵波方位各向异性定量预测火山岩裂缝[J]. 石油物探, 2014, 53(4): 477–483.
JIA Yuewei, WEI Shuijian, LYU Lin. Application of seismic P-wave azimuthal anisotropy in volcanic fracture prediction[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 477–483. |
| [16] |
王庆如, 李敬功.
碳酸盐岩气藏储量参数测井评价方法[J]. 岩性油气藏, 2013, 25(6): 98–102.
WANG Qingru, LI Jinggong. Logging evaluation method of reserve parameters of carbonate gas reservoir[J]. Lithologic Reservoirs, 2013, 25(6): 98–102. |
| [17] |
张娟, 周文, 邓虎成, 等.
麻黄山地区延安组、延长组储层裂缝特征及识别[J]. 岩性油气藏, 2009, 21(4): 53–57.
ZHANG Juan, ZHOU Wen, DENG Hucheng, et al. Fracture identification of reservoir of Yan'an and Yanchang Formation in Mahuangshan Area[J]. Lithologic Reservoirs, 2009, 21(4): 53–57. |
| [18] |
先伟, 吴伟航, 李小刚, 等.
双侧向测井裂缝参数解释在伊朗Aran油田的应用[J]. 岩性油气藏, 2008, 20(3): 89–94.
XIAN Wei, WU Weihang, LI Xiaogang, et al. Application of dual laterolog interpretation of fracture parameters in Aran Field, Iran[J]. Lithologic Reservoirs, 2008, 20(3): 89–94. |
| [19] |
王孟华, 崔永谦, 张锐峰, 等.
泥灰岩裂缝储层预测方法研究:以束鹿凹陷为例[J]. 岩性油气藏, 2007, 19(3): 114–119.
WANG Menghua, CUI Yongqian, ZHANG Ruifeng, et al. Prediction method for marl fractured reservoir:an example from Shulu Sag[J]. Lithologic Reservoirs, 2007, 19(3): 114–119. |
| [20] |
刘清, 黄兆华, 姚力文.
Rough集理论:现状与前景[J]. 计算机科学, 1997, 24(4): 2–4.
LIU Qing, HUANG Zhaohua, YAO Liwen. Rough set theory:present state and prospects[J]. Computer Science, 1997, 24(4): 2–4. |
| [21] |
王国胤, 姚一豫, 于洪.
粗糙集理论与应用研究综述[J]. 计算机学报, 2009, 32(7): 1229–1246.
WANG Guoyin, YAO Yiyu, YU Hong. A survey on Rough Set theory and applications[J]. Chinese Journal of Computers, 2009, 32(7): 1229–1246. |
| [22] | RÜGRE A. Reflection coefficients and azimuthal AVO analysis in anisotropic media[M]. Tulsa: Society of Exploration Geophysicists, 2002: 140-147. |
| [23] | MALLICK S, CRAFT K L, MEISTER L J, et al. Determination of the principal directions of azimuthal anisotropy form P-wave seismic data[J]. Geophysics, 1998, 63(2): 692–706. DOI:10.1190/1.1444369 |
| [24] |
黄捍东, 刘徐敏, 蔡燕杰, 等.
综合利用测井-地震方法识别火成岩裂缝[J]. 石油地球物理勘探, 2015, 50(5): 942–950.
HUANG Handong, LIU Xumin, CAI Yanjie, et al. Igneous rock fracture prediction with well logging and seismic data[J]. Oil Geophysics Prospecting, 2015, 50(5): 942–950. |


