井眼轨迹定位是导向钻井的基本问题。为满足井眼轨道设计、井眼轨迹监测与控制的需求,往往以井口为原点建立1个空间直角坐标系,其中3个坐标轴分别指向正北、正东及垂直方向,称为井口坐标系。井眼轨道设计需要先确定出靶点相对于井口的空间位置,而井眼轨迹监测和控制需要随时确定出井眼轨迹上各测点的空间位置,这些都需要确定井眼轨迹上某点在井口坐标系下的空间坐标,称为井眼轨迹定位。
现行定位方法采用地图投影的纵横坐标及高程差来确定靶点与井口间的相对位置,其指北基准为地图投影纵坐标北(或称网格北);用井口处的磁偏角来归算全井的实钻井眼轨迹,没有考虑磁偏角随时间和空间的变化。事实上,地图投影存在变形,地球椭球面并非水平面,各测点处的磁偏角不同,因此现行定位方法存在固有缺陷和较大误差。笔者基于大地测量学和地磁学原理,研究提出了设计井眼轨道和实钻井眼轨迹的定位方法。应用实例表明,笔者提出的新定位方法从根本上消除了现行定位方法的缺陷及误差,能精准定位井眼轨迹。
1 地球椭球及坐标系统 1.1 地球椭球的几何形状地球的形状接近于一个三轴扁梨形椭球,南胀北缩、东西略扁,而且地球的自然表面起伏不平、很不规则。为便于进行测量和计算,通常将其模型化为椭球,称之为地球椭球。而代表地球自然表面的曲面称之为大地水准面,它是由静止海水面和其向大陆延伸所形成的闭合曲面,处处垂直于铅垂线。因此,大地水准面是重力等位面,物体在这个曲面上运动时重力不做功,水在该曲面上也不会流动。
地球椭球是经过适当选取的旋转椭球,是椭圆绕其短轴旋转而成的几何体[1],如图 1所示。过旋转轴的平面称为子午面,该平面与椭球面的交线为椭圆,称为子午圈或子午椭圆。而垂直于旋转轴的平面与椭球面的交线为圆形,称为平行圈。

|
| 图 1 地球椭球及坐标系统 Fig.1 Earth ellipsoid and coordinate systems |
旋转椭球的形状和大小常用子午椭圆的5个基本几何参数来表征,包括长半轴a、短半轴b、扁率f、第一偏心率e和第二偏心率e′等参数。只需知道其中的2个参数,但至少要有1个长度参数,便可确定旋转椭球的形状和大小。截至目前,已经利用天文大地测量、重力测量和空间大地测量等方法推算出多个地球椭球,如克拉索夫斯基椭球、1975国际椭球、WGS-84椭球等。
1.2 大地基准及高程描述物体位置的常用参数是坐标,而坐标隶属于坐标系。在大地测量学中,确定坐标系与地球椭球之间的关系是通过大地基准来实现的,这种具有大地基准的坐标系称为坐标参考系。大地基准定义了相对于地球中心的参考椭球的位置和方向,进而可以确定坐标系的原点和方向。参考椭球的大小和形状应与研究区域的大地水准面有最佳吻合,这不仅要求椭球短轴与地球自转轴配准,还要使椭球的零度经线与定义的起始子午线相一致[2]。
由于地球质量分布的不均匀性,导致大地水准面的形状非常复杂,目前还不能精确确定大地水准面。为此,常采用正常重力代替实际重力来确定大地水准面,由此得到的水准面称为似大地水准面。似大地水准面很接近于大地水准面,二者在海洋上完全重合、在陆地上几乎重合、在山区也只有2~4 m的差异。尽管似大地水准面不是严格意义上的水准面,但是能严密地解决关于地球自然地理形状的有关问题。用大地水准面和似大地水准面作为基准面的高程系统,分别称为正高和正常高系统。我国采用正常高系统,并建立了1956年黄海高程系和1985国家高程基准[3]。
1.3 地球椭球定位及定向地球椭球定位是指确定地球椭球中心的位置,可分为局部定位和地心定位。局部定位要求在一定范围内椭球面与大地水准面有最佳吻合,但对椭球的中心位置无特殊要求;地心定位要求在全球范围内椭球面与大地水准面有最佳吻合,同时要求椭球中心与地球质心一致或最为接近[1]。
地球椭球定向是指确定地球椭球旋转轴的方向,局部定位和地心定位都应满足2个平行条件[1]:1) 椭球短轴平行于地球自转轴;2) 大地起始子午面平行于天文起始子午面。这2个平行条件是人为规定的,其目的是简化大地坐标、大地方位角与天文坐标、天文方位角之间的换算。
已知长半轴a和扁率f等参数,经过局部定位和定向,并与某地区大地水准面有最佳拟合的地球椭球,叫作参考椭球。除满足地心定位和双平行条件外,能在全球范围内与大地体最密合的地球椭球,叫作总地球椭球[1]。
1.4 坐标系统固定在地球上并随地球一起旋转的坐标系称为地固坐标系。它是以旋转椭球为参照体建立的坐标系,用于研究地球上物体的位置和运动。如果忽略地球的潮汐和板块运动,地面上每个点的坐标在地固坐标系中保持不变,因此便于描述地球表面点的空间位置。
根据坐标系原点位置的不同,地固坐标系分为参心坐标系和地心坐标系。参心坐标系以参考椭球面为参考面,原点位于参考椭球中心;地心坐标系以总地球椭球面为参考面,原点位于地球质心[1-2]。参心坐标系和地心坐标系都具有空间直角坐标系和大地坐标系2种形式。
空间直角坐标系用三维直角坐标来确定空间点的位置,如图 1所示。Z轴为地球椭球的旋转轴,指向地球北极;X轴为起始子午面与赤道面的交线,指向椭球面;Y轴在赤道面内并与X轴正交,即指向地理东方向。大地坐标系是以地球椭球的赤道面和起始子午面为起算面,以地球椭球面为参考面而建立的地球椭球面坐标系。它是大地测量的基本坐标系,其参数包括大地经度L、大地纬度B和高程(或大地高)h。大地经度L是子午面与起始子午面之间的夹角,自起始子午面起算,向东为正称为东经,向西为负称为西经。大地纬度B是椭球面法线与赤道面之间的夹角,自赤道面起算,向北为正称为北纬,向南为负称为南纬。高程h是空间点相对于高程基准面的高度,而相对于地球椭球面的高度称为大地高。我国已先后建立了1954年北京坐标系、1980西安坐标系、新1954北京坐标系和2000国家大地坐标系等4个国家大地坐标系[2-3]。
2 地磁场及地磁参考场地球具有磁场,且具有复杂的时空特性及演化规律。就磁偏角而言,世界各地差异很大。日本的磁偏角很小,而格陵兰中部的磁偏角却高达60°。磁偏角也在不断变化,英国伦敦1600年的磁偏角为北偏东8°,以后沿逆时针方向转动,到1800年为北偏西24°,在200年里磁偏角摆动了32°,随后它又往回移动,到1950年只有北偏西8°。我国境内的磁偏角变化较小,一般年变化率只有2′左右。东部和沿海地区的磁偏角偏西,而西部和南海地区的磁偏角偏东,纬度越高磁偏角越大。
地磁场可分为稳定磁场和变化磁场,其中稳定磁场包括主磁场和局部异常磁场。稳定磁场也称为基本磁场,是地磁场的主要组成部分,占总磁场99%以上,且变化缓慢[4]。自1968年起,国际地磁学与高空物理学协会(IAGA)以各国地磁测量和地磁图为基础,给出了以5年为间隔的国际参考地磁场IGRF (international geomagnetic reference field)[5],并绘制出相应的世界地磁图。IGRF模型采用球谐分析方法来描述地磁场,地固空间直角坐标系下的地磁场分量为:
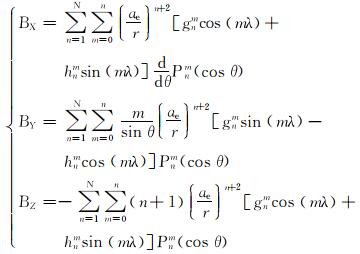
|
(1) |
式中:BX,BY和BZ分别为地固空间直角坐标系下X,Y和Z方向上的地磁场分量,nT;ae为地磁参考半径,m;r为径向距离,m;λ为东经,(°);θ为地心余纬度,(°);gnm和hnm为高斯球谐系数,nT;Pnm(cos θ)为n阶m次施密特型缔合勒让德函数;N为最高阶数。
根据地固空间直角坐标系的地磁场分量(BX,BY,BZ),可求得井口坐标系下的地磁场分量(BN,BE,BH),进而求得磁偏角δ[6]:

|
(2) |
式中:BN,BE和BH分别为井口坐标系下的地磁场分量,nT;δ为磁偏角,(°)。
磁偏角是总磁场强度的水平分量偏离地理北向的角度,也是磁子午线与真子午线之间的夹角,自真子午线起算,磁偏角偏东时为正,偏西时为负。
3 设计井眼轨道定位在设计井眼轨道时,首先应确定靶点相对于井口的位置,即靶点在井口坐标系下的空间坐标。现行方法将大地水准面近似为水平面并基于地图投影坐标进行定位,方法存在缺陷, 导致结果存在较大误差,严重影响了井眼轨道的设计精度。基于地球椭球及其解算原理,笔者提出了真三维井眼定位方法,消除了现行定位方法的缺陷及误差[7-8]。
真三维井眼定位方法以真北方向为指北基准,首先根据井口和靶点的大地坐标及大地高(Lo,Bo,ho)和(Lt,Bt,ht),计算井口和靶点在地固空间直角坐标下的坐标(Xo,Yo,Zo)和(Xt,Yt,Zt),其计算公式为:
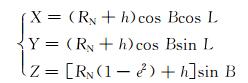
|
(3) |
然后再计算靶点t在井口坐标系O-NEH下的坐标(Nt,Et,Ht),其计算公式为:

|
(4) |
式中:h为大地高,m;(Nt,Et,Ht)靶点t在井口坐标系O-NEH下的坐标,m;(Xo,Yo,Zo)和(Xt,Yt,Zt)分别为井口和靶点在地固空间直角坐标下的坐标,m;Lo和Bo分别为井口的大地经度和大地纬度,(°);RN为卯酉圈的曲率半径,m。
这样,根据靶点相对于井口的空间坐标(Nt,Et,Ht),便可算得靶点的垂深、水平位移等参数,进而可进行井眼轨道设计。
4 实钻井眼轨迹定位利用MWD等仪器可获得实钻井眼轨迹上一系列测点的测斜数据,包括井深、井斜角和方位角(Di,αi,φi)(i =1,2,…,n),其中n为测点数。井眼轨迹监测的基本任务是求得各测点的空间坐标(Ni,Ei,Hi)。第1个测点与井口构成第1个测段,其中井口的大地坐标、空间坐标、磁偏角等参数均为已知数据,所以只需归算第1个测点的方位角, 便可算得该测点的空间坐标。对于第2个测段来说,由于上测点的各参数已由第1个测段求得,所以只需归算下一测点的方位角并计算其空间坐标。据此逐测段类推,便可计算出全井的实钻井眼轨迹。可见,在每个测段内,首先应求得下一测点处的磁偏角,并将下一测点的实测方位角归算为真方位角;然后再按井眼轨迹模型算得测段内的坐标增量,便可算得下一测点的空间坐标。计算公式为:
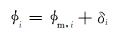
|
(5) |
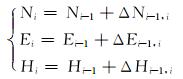
|
(6) |
式中:φm为磁方位角,(°);φi为i测点的方位角,(°);(Ni,Ei,Hi)分别为i测点的空间坐标,m。
然而,每个测点的空间位置不同,在随钻过程中的测量时间也不同,所以每个测点的磁偏角δi各不相同。但是,在用式(5) 归算方位角时,还不知道下一测点的空间位置,所以需要使用迭代法来求取各测点的磁偏角。此外,在用地磁参考场模型求取磁偏角时,由于需要用到各测点处的大地坐标,所以应先利用式(3) 求得各测点在地固空间直角坐标系下的坐标(Xi,Yi,Zi),然后再计算其大地坐标,计算公式为:
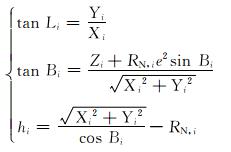
|
(7) |
采用我国2000国家大地坐标系和IGRF-12国际地磁参考场,大地坐标系参考椭球的长半轴a=6 378 137.0 m、短半轴b=6 356 752.314 1 m、扁率为1/298.257 222 101。某水平井井口和靶点的大地坐标及大地高见表 1。按真三维井眼定位方法,先求得地固空间直角坐标系下井口和靶点的坐标,再求得井口坐标系下的靶点坐标,结果见表 2。
| 定位点 | 经度 | 纬度 | 大地高/m |
| 井口 | 119°45′E | 50°N | 700.00 |
| A靶点 | 119°45′11.3775″E | 50°0′5.3279″N | -1 597.99 |
| B靶点 | 119°47′53.6754″E | 50°0′53.3435″N | -1 596.85 |
| 定位点 | X/m | Y/m | Z/m | N/m | E/m | H/m | 水平位移/m | 平移方位角/(°) |
| 井口 | -2 038 613.23 | 3 566 833.38 | 4 863 325.27 | 0 | 0 | 0 | 0 | |
| A靶点 | -2 038 014.36 | 3 565 329.08 | 4 861 670.69 | 164.58 | 226.53 | 2 298.00 | 280.00 | 54.00 |
| B靶点 | -2 040 254.76 | 3 562 738.95 | 4 862 624.76 | 1 648.86 | 3 456.90 | 2 298.00 | 3 830.00 | 64.50 |
| 注:X,Y和Z为地固空间直角坐标系下的坐标;北坐标、东坐标、垂深为井口坐标系下的坐标。 | ||||||||
为节省篇幅,假设实钻井眼轨迹的测点很稀疏,且测量时刻截取到日期。根据自然曲线法,采用真三维井眼定位方法对实钻井眼轨迹进行了定位计算,结果见表 3。
| D/m | α/(°) | φm/(°) | 测量时刻 | δ/(°) | φT/(°) | N/m | E/m | H/m | 水平长度/m | 水平位移/m | 平移方位角/(°) |
| 0 | 0 | 2016-02-07 | -10.316 | 0 | 0 | 0 | 0 | 0 | |||
| 2 000.00 | 0 | (60.00) | 2016-03-26 | -10.332 | (49.660) | 0 | 0 | 2 000.00 | 0 | 0 | (49.66) |
| 2 170.00 | 45.00 | 60.00 | 2016-05-15 | -10.340 | 49.660 | 41.04 | 48.32 | 2 153.05 | 63.40 | 63.40 | 49.66 |
| 2 300.00 | 45.00 | 65.00 | 2016-08-08 | -10.352 | 54.648 | 97.42 | 120.89 | 2 244.98 | 155.32 | 155.26 | 51.14 |
| 2 440.00 | 90.00 | 70.00 | 2016-10-01 | -10.360 | 59.640 | 165.53 | 226.90 | 2 297.19 | 281.37 | 280.86 | 53.89 |
| 6 000.00 | 90.00 | 80.00 | 2016-12-19 | -10.388 | 69.612 | 1 689.17 | 3 439.40 | 2 297.19 | 3 841.37 | 3 831.81 | 63.84 |
| 注:井深、井斜角和磁方位角为测量数据;磁偏角、真方位角、北坐标、东坐标、垂深、水平长度、水平位移、平移方位角为计算结果。磁(真)方位角括号内的数据为定向方位角,平移方位角括号内的数据类似于方位角。 | |||||||||||
计算结果表明,真三维井眼定位方法与现行定位方法求得的靶点与井口的相对位置不同,进而导致井眼轨道的设计结果不同。现行定位方法算得的靶点垂深偏小、水平位移偏大。实钻井眼轨迹上每个测点的磁偏角各不相同,新的实钻轨迹定位方法考虑了磁偏角随时间和空间的变化,提高了井眼轨迹监测的精度和可靠性。
6 结论1) 由于地图投影存在变形、地球椭球面并非水平面、磁偏角随时空变化等原因,现行定位方法存在固有缺陷和较大误差。
2) 现行定位方法算得的靶点垂深偏小、水平位移偏大。基于地球椭球的靶点定位方法不涉及地图投影问题,能精准定位靶点相对于井口的空间位置。
3) 地磁场随时间和空间变化,井眼轨迹上各测点处的磁偏角不同,利用国际地磁参考场求得的磁偏角等数据能满足钻井工程的精度要求。对于水平位移大、施工周期长的定向井,应考虑各测点处磁偏角的变化来定位井眼轨迹。
4) 新定位方法能提高井眼轨道设计与井眼轨迹监测的精度及可靠性,值得推广应用。
| [1] |
孔祥元, 郭际明, 刘宗泉.
大地测量学基础[M]. 2版. 武汉: 武汉大学出版社, 2010: 99-206.
KONG Xiangyuan, GUO Jiming, LIU Zongquan. Foundation of geodesy[M]. 2nd ed. Wuhan: Wuhan University Press, 2010: 99-206. |
| [2] |
王美玲, 付梦印.
地图投影与坐标变换[M]. 北京: 电子工业出版社, 2014: 15-18.
WANG Meiling, FU Mengyin. Map projection and coordinate transformation[M]. Beijing: Publishing House of Electronics Industry, 2014: 15-18. |
| [3] |
GB/T 17159-2009大地测量术语[S].
GB/T 17159-2009 Geodetic term[S]. |
| [4] |
徐文耀.
地磁学[M]. 北京: 地震出版社, 2003: 1-121.
XU Wenyao. Geomagnetics[M]. Beijing: Seismological Press, 2003: 1-121. |
| [5] | IAGA, Working Group V-MOD. International geomagnetic reference field:the eleventh generation[J]. Geophysical Journal International, 2010, 183(3): 1216–1230. DOI:10.1111/j.1365-246X.2010.04804.x |
| [6] |
石在虹, 滕少臣, 刘子恒.
国际地磁参考场解算方法及石油工程应用[J]. 石油钻采工艺, 2016, 38(4): 409–414.
SHI Zaihong, Teng Shaochen, Liu Ziheng. Algorithm for international geomagnetic reference field and its application in petroleum engineering[J]. Oil Drilling & Production Technology, 2016, 38(4): 409–414. |
| [7] |
刘修善.
基于地球椭球的真三维井眼定位方法[J]. 石油勘探与开发, 2017, 44(2): 275–280.
LIU Xiushan. A true three-dimensional wellbore positioning method based on the earth ellipsoid[J]. Petroleum Exploration and Development, 2017, 44(2): 275–280. |
| [8] |
刘修善.
考虑磁偏角时空变化的实钻轨迹精准定位[J]. 石油学报, 2017, 38(6): 705–709.
LIU Xiushan. Positioning the drilled borehole trajectories considering the magnetic declination change in space-time[J]. Acta Petrolei Sinica, 2017, 38(6): 705–709. DOI:10.7623/syxb201706010 |


