近年来,页岩气的勘探与开发成为国内外的热点[1-4]。页岩气密度是页岩气藏评价和开发所需要的重要物性参数之一[5]。常用的气体密度确定方法有图版法和基于理想气体状态方程的计算方法,但前者使用不便,且精度不高,特别是在页岩气藏数值模拟中难以应用;后者的计算结果误差较大。国外学者对气体密度计算方法进行了大量的研究:1873年,荷兰物理学家J.D.van der Waals提出了立方型状态方程--范德华方程[6],通过考虑真实气体分子的体积,对理想气体状态方程进行了修正,以提高气体密度的计算精度[7],但该方程不能很好地适用于高温高压条件;此后,许多学者又提出了Redlich-Kwong (RK)、Soave-Redlich-Kwong (SRK)、Peng-Robinson (PR)和Patel-Teja (PT)等状态方程[8-9],但这些方程在计算混合气体密度时的精度仍然不高。由于页岩气不是单组分气体,而是含有甲烷、氮气和二氧化碳等气体的混合气体,此外页岩气藏的温度和压力也远达不到理想气体的条件, 因此,基于理想状态方程的气体密度计算方法即使经过校正,也难以使计算结果达到理想的精度[10]。为了快速准确地计算页岩气密度,笔者基于页岩气密度计算适应性较好的SRK状态方程,在比容迭代计算中,引入对比压力和对比温度的函数修正式,建立了页岩气密度计算新方法,并编制了计算机程序,210个样点的计算结果对比验证了该方法的准确性。
1 基于SRK状态方程的页岩气密度计算方法 1.1 SRK状态方程目前,SRK状态方程与PR状态方程在石油、天然气领域比较常用[11-13],其中SRK状态方程比较适合计算石油烃类物质混合物密度,尤其在计算纯烃和氮气、氢气等非极性气体密度时具有较高的精度。SRK状态方程为:
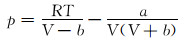
|
(1) |
式中:R为通用气体常数,8.314 J/(mol·K);p为系统压力,Pa;T为温度,K;V为比容,m3/mol;a和b为状态方程系数。
1.2 特征参数计算SRK状态方程是基于纯物质而获得的,其中的临界温度、临界压力、偏心因子和相对分子质量等特征参数也是基于纯物质的,而对于页岩气等混合气体,其特征参数不能直接代入式(1)进行密度计算。为此,笔者采用了拟临界参数法,将页岩气近似等效为拟纯物质,并具有虚拟的特征参数,然后通过混合法则计算其特征参数,并代入式(1)计算其比容。笔者采用文献[11, 14]中物质的量组成加权平均混合法则,计算上述4个拟特征参数:

|
(2) |
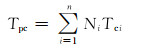
|
(3) |
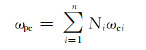
|
(4) |
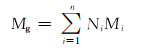
|
(5) |
式中:ppc为页岩气的拟临界压力,MPa;Tpc为页岩气的拟临界温度,K;ωpc为页岩气的似偏心因子;Mg为页岩气的视相对分子质量;n为页岩气的组分个数;Ni为页岩气中第i个组分的摩尔分数;pci为页岩气中第i个组分的临界压力,MPa;Tci为页岩气中第i个组分的临界温度,K;ωci为页岩气中第i个组分的偏心因子;Mi为页岩气中第i个组分的相对分子质量。
为了提高计算结果的正确性,笔者选择了美国国家标准与技术研究院(National Institute of Standards and Technology,NIST)公布的页岩气数据(见表 1[15]),利用式(2)-式(5)计算得到页岩气的4个特征参数:ppc=4.827 7 MPa,Tpc=204.073 3 K,ωpc=0.026 5,这3个参数用于计算式(1)中的系数a和b,计算方法见文献[11];Mg=18.498 4,用于摩尔密度和质量密度的转换。
| 组分 | 分子式 | 摩尔分数 | 相对分子质量 | 临界压力/MPa | 临界温度/K | 偏心因子 |
| 甲烷 | CH4 | 0.894 3 | 16.00 | 4.604 | 190.55 | 0.010 4 |
| 乙烷 | C2H6 | 0.018 3 | 30.10 | 4.880 | 305.43 | 0.098 8 |
| 丙烷 | C3H8 | 0.004 9 | 44.10 | 4.249 | 369.82 | 0.152 4 |
| 正丁烷 | nC4H10 | 0.002 5 | 58.10 | 3.797 | 425.16 | 0.201 0 |
| 正戊烷 | nC5H12 | 0.002 7 | 72.20 | 3.369 | 469.60 | 0.253 9 |
| 二氧化碳 | CO2 | 0.049 1 | 44.01 | 7.382 | 304.14 | 0.225 0 |
| 硫化氢 | H2S | 0.022 0 | 34.00 | 9.005 | 373.50 | 0.100 0 |
| 氮气 | N2 | 0.006 2 | 28.00 | 3.399 | 126.11 | 0.040 0 |
为了便于求解比容,对式(1)两边同时乘以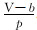
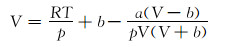
|
(6) |
令V0=
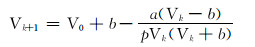
|
(7) |
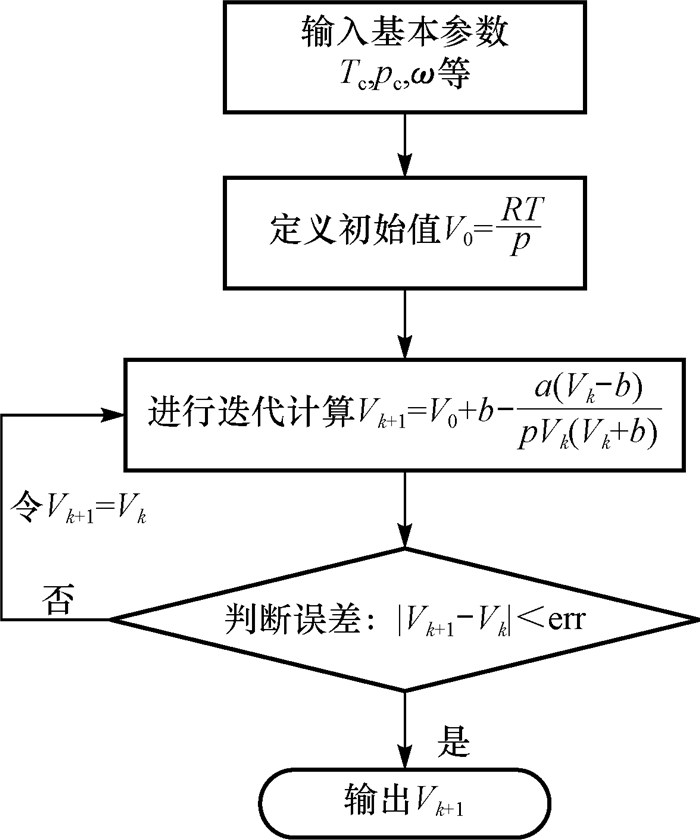
式(7)即为基于SRK状态方程的页岩气密度计算公式(以下简称SRK方法)。采用牛顿迭代方法求解比容,在迭代过程中设置迭代误差值收敛条件为0.000 1。由于比容V与摩尔密度互为倒数,计算出比容后即可求出页岩气的摩尔密度,将摩尔密度乘以页岩气的摩尔质量(数值上等于页岩气视相对分子质量)即可以得到页岩气的质量密度。计算步骤见图 1。
|
| 图 1 基于SRK状态方程的页岩气比容计算程序框图 Fig.1 The calculating program diagram for shale gas specific volume by SRK equation of state |
为定量分析SRK方法的精度,笔者通过调研国内外大量文献,将NIST[15]公布的页岩气密度数据作为精确值,将应用SRK方法计算的210个样点的页岩气密度与其进行了对比,并计算了相对误差,结果见表 2(笔者选择了7个压力,每个压力下计算30个温度点的页岩气密度,共210个样点,表 2中列出了每个压力下30个温度点中页岩气密度的最大和最小误差值)。相对误差的计算公式为:
| 压力/MPa | 相对误差,% | |
| 最小 | 最大 | |
| 1 | -0.08 | -0.05 |
| 5 | -0.55 | -0.55 |
| 10 | -7.88 | -1.20 |
| 15 | -11.10 | -1.73 |
| 20 | -9.33 | -2.03 |
| 25 | -5.82 | -2.10 |
| 30 | -3.74 | -1.97 |
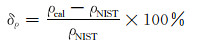
|
(8) |
式中:δρ为相对误差;ρcal为计算的页岩气密度,kg/m3;ρNIST为NIST公布的页岩气密度,kg/m3。
由表 2可知,SRK方法计算得到的页岩气密度相对误差为-11.10%~-0.05%,局部相对误差绝对值超过了10%,表明其计算精度不够高;所有相对误差皆为负值,说明密度计算结果普遍偏低。
2.2 SRK方法的改进计算结果对比表明,SRK方法计算的页岩气密度普遍偏低,分析认为:在低温下,由于页岩气是多组分的混合气体,而SRK状态方程中反映页岩气不同分子间引力的系数a和斥力的系数b无法算准,用文献[11]中的方法计算的引力系数偏小,导致计算的比容偏大(即密度偏小),这是造成SRK方法计算结果误差大的主要原因。因此,需要对SRK方法进行改进,以提高页岩气密度计算精度。通常的改进思路是观测分析页岩气物理性质及其影响因素的关系,通过合理的猜想,给出假定的修正式,通过试算和拟合确定修正式中的系数,而最重要的是如何确定修正式中的关键参数。
对比温度和对比压力是表征气体基本对比状态的2个无因次参数:一方面,这2个参数同时把影响页岩气密度的温度和压力2个主变量及表征物质临界特征状态的临界温度和临界压力包括进来;另一方面,对比压力和对比温度是2个无量纲的参数,在建立修正式时容易满足量纲的和谐性。为此,笔者在改进SRK方法时引入了对比压力和对比温度,通过这2个参数体现温度和压力对修正系数的影响,以实现修正系数的定量计算,在比容迭代中实现逐次修正的目的。
根据文献[10]对纯物质对比参数定义,页岩气的对比压力和对比温度的表达式为:
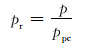
|
(9) |
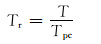
|
(10) |
式中:pr为页岩气的对比压力;Tr为页岩气的对比温度。
物质处于临界状态时的压力和温度为临界压力和临界温度,页岩气的拟临界参数计算见式(2)-式(5)。
引入修正系数λ,将式(7)变为:
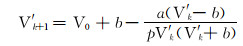
|
(11) |
其中
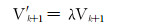
|
(12) |
将式(12)代入式(11),得到改进的SRK方法中计算比容的新公式:
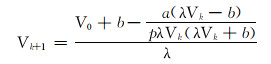
|
(13) |
对于混合气体,由于压力和温度是影响其密度的关键因素,则设定修正系数λ的表达式为:
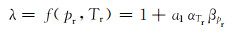
|
(14) |
式中:a1为拟合系数;αTr为温度对比容影响的修正项,通过对比温度实现该参数的计算;βpr为压力对比容影响的修正项,通过对比压力实现该参数的计算。
αTr和βpr的表达式分别为:
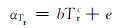
|
(15) |
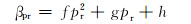
|
(16) |
为了确定拟合系数a1和式(15)、式(16)中的系数,根据比容的定义、摩尔密度和质量密度的关系,可得:
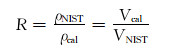
|
(17) |
从美国NIST公布的页岩气密度数据与SRK方法计算密度数据中对应选取30个值,通过拟合得到:a1=8.501,b=0.015 43,c=-0.215,e=1.0,f=-0.000 47,g=0.001 58,h=-0.002 49。将其代入式(15)和式(16)得:
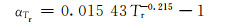
|
(18) |
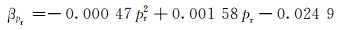
|
(19) |
在应用改进的SRK方法计算页岩气密度时,也采用牛顿迭代方法,其计算步骤与SRK方法一样,只需将图 1中比容迭代计算公式用式(13)替换即可。
3 计算实例利用表 1中的数据,采用改进的SRK方法计算了210个样点的页岩气密度(样点选取与表 2相同),并利用式(8)计算其与NIST公布的页岩气密度值的相对误差,结果见表 3。
| 压力/MPa | 相对误差,% | |
| 最小 | 最大 | |
| 1 | -0.08 | -0.05 |
| 5 | -0.27 | 2.11 |
| 10 | -0.69 | 1.88 |
| 15 | -2.39 | 1.14 |
| 20 | -1.45 | 0.46 |
| 25 | -1.66 | 0.88 |
| 30 | -1.80 | -0.44 |
由表 3可知,改进的SRK方法计算得到的页岩气密度相对误差为-2.39%~2.11%,相对误差绝对值最大为2.39%。对比表 2和表 3中的相对误差可以看出,与SRK方法相比,采用改进的SRK方法计算页岩气密度计算精度明显提高。
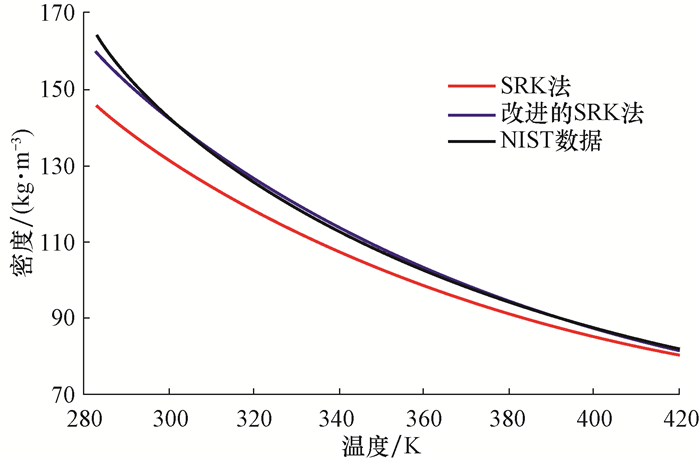
图 2为压力15 MPa条件下,应用SRK方法和改进的SRK方法得到的页岩气密度以及NIST标准页岩气密度随温度的变化曲线。
|
| 图 2 两种方法计算的页岩气密度与NIST数据的对比(压力p=15 MPa) Fig.2 Comparison of calculated shale gas density with NIST data by two methods (pressure=15 MPa) |
由图 2可知,高温条件下(T>350 K),2种方法计算的页岩气密度与NIST标准值相差较小;随着温度的降低,SRK方法的计算误差变大,但改进的SRK方法的计算值与NIST标准值仍能基本保持一致,计算精度明显好于SRK方法。
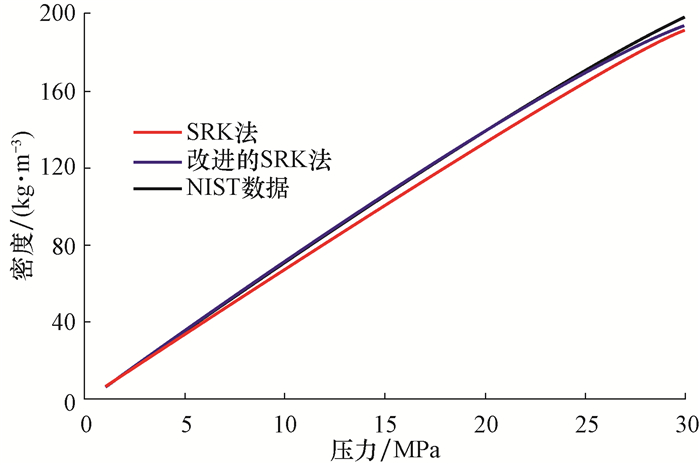
图 3为温度353.15 K条件下,应用SRK方法和改进的SRK方法得到的页岩气密度和NIST标准页岩气密度随压力的变化曲线。
|
| 图 3 两种方法计算的页岩气密度与NIST数据的对比(温度T=353.15 K) Fig.3 Comparison of calculated shale gas density with NIST data by two methods (Temperature=353.15 K) |
由图 3可知,低压条件下(p<10 MPa),2种方法计算的页岩气密度与NIST标准值非常接近;随着压力升高,改进的SRK方法的计算值与NIST标准值基本一致,但SRK方法的计算误差稍有增大。这表明改进的SRK方法的计算精度要优于SRK方法。
4 结论与建议1)为提高页岩气密度计算精度,通过引入对比压力与对比温度,对SRK方法进行了改进,建立了计算页岩气密度的新方法。
2) 210个样点的计算结果对比表明:改进的SRK方法的计算精度明显优于SRK方法,能满足工程应用的要求。
3)利用美国NIST标准页岩气密度验证了改进的SRK方法的正确性,但由于我国页岩气的成分、特征参数和不同温度与压力条件下的密度数据缺乏,故该方法对我国页岩气密度计算的适用性有待于进一步验证。建议进一步开展我国不同地区页岩气密度的实验研究,以提高该计算方法的通用性和可靠性。
| [1] |
路保平.
中国石化页岩气工程技术进步及展望[J]. 石油钻探技术 , 2013, 41 (5) : 1–8.
LU Baoping. Sinopec engineering technical advance and its developing tendency in shale gas[J]. Petroleum Drilling Techniques , 2013, 41 (5) : 1–8. |
| [2] |
石艺.
页岩气的发展现状和未来走向[J]. 石油钻采工艺 , 2012, 34 (4) : 70.
SHI Yi. Present situation and future trend of shale gas development[J]. Oil Drilling & Production Technology , 2012, 34 (4) : 70. |
| [3] | BUST V K, MAJID A A, OLETU J U, et al. The petrophysics of shale gas reservoirs:technical challenges and pragmatic solutions[J]. Petroleum Geoscience , 2012, 19 (2) : 91–103. |
| [4] |
薛承瑾.
国内页岩气有效开采值得关注的几个问题[J]. 石油钻探技术 , 2012, 40 (4) : 1–6.
XUE Chengjin. Noteworthy issues on effective production of shale gas resource in China[J]. Petroleum Drilling Techniques , 2012, 40 (4) : 1–6. |
| [5] |
赵良孝, 邢会民.
天然气储层评价的新参数:充盈度[J]. 天然气工业 , 2010, 30 (6) : 31–34.
ZHAO Liangxiao, XING Huimin. A new parameter for gas reservoir appraisal:suffusive degree[J]. Natural Gas Industry , 2010, 30 (6) : 31–34. |
| [6] | van der WAALS J D. On the continuity of the gaseous and liquid states[M]. Amsterdam: North-Holland Publishing Co , 1988 . |
| [7] | BERNE B J. Physical chemistry:an advanced treatise (vol 8a)[M]. New York: Academic Press , 1971 . |
| [8] | SOAVE G. Equilibrium constants from a modified Redlich-Kwong Equation of state[J]. Chemical Engineering Science , 1972, 27 (6) : 1197–1203. DOI:10.1016/0009-2509(72)80096-4 |
| [9] | AHMED T. Equations of state and PVT analysis[M]. Houston: Gulf Publishing Company , 2006 : 365 -367. |
| [10] |
吴明清, 李珍义, 张小川.
计算法天然气密度测量不确定度分析[J]. 工业计量 , 2007 (supplement 1) : 127–132.
WU Mingqing, LI Zhenyi, ZHANG Xiaochuan. Analysis on the uncertainty of measurement results on natural gas density[J]. Industrial Measurement , 2007 (supplement 1) : 127–132. |
| [11] |
郭天民.
多元气-液平衡和精馏[M]. 北京: 石油工业出版社 ,1983 : 36 -42.
GUO Tianmin. Multicomponent gas-liquid equilibrium and distillation[M]. Beijing: Petroleum Industry Press , 1983 : 36 -42. |
| [12] |
韩晓红, 陈光明, 王勤, 等.
状态方程研究进展[J]. 天然气化工 , 2005, 30 (5) : 55–64.
HAN Xiaohong, CHEN Guangming, WANG Qin, et al. A review on equations of state[J]. Natural Gas Chemical Industry , 2005, 30 (5) : 55–64. |
| [13] | PENG D Y, ROBINSON D B. A new two-constant equation of state[J]. Industrial & Engineering Chemistry Fundamentals , 1976, 15 (1) : 59–64. |
| [14] |
陈元千.
计算凝析气藏地质储量和重组总井流体组分的方法[J]. 断块油气田 , 1997, 4 (5) : 1–4.
CHEN Yuanqian. The methods of calculating original petroleum in place and recombining composition of total well fluid for gas condensate reservoirs[J]. Fault-Block Oil & Gas Field , 1997, 4 (5) : 1–4. |
| [15] | LEMMON E W, HUBER M L, McLINDEN M O. NIST standard reference database:reference fluid thermodynamic and transport properties[M]. Gaithersburg: National Institute of Standards and Technology , 2002 . |




