低渗透气藏的产气界面对计算气藏的含气面积、气层有效厚度和储量等极为重要[1-3]。由于低渗透气藏孔隙结构差,孔隙与喉道细小,致使气水分异作用减弱,存在较高的气水过渡带,影响气藏开发效果[4-5]。准确确定低渗透气藏的产气界面(储层可动流体仅为气相的界面)[6],能够指导射孔层位和后期的开发方案调整[4]。目前低渗透气藏计算产气界面相关数据的方法很多,但应用时均存在一定的限制条件,且未考虑气水过渡带的影响,若气井位于过渡带,则会出现气水两相渗流,由于可动水对气相相对渗透率的影响较大,将严重影响气井的压力波及半径和气井产能的发挥,导致气井产能迅速下降[5, 7],因此有必要对产气界面开展研究,明确产气不产水层的位置。由于束缚水饱和度、气柱高度主要受储层物性影响[8],因此可以通过岩心试验建立物性与低渗透气藏的束缚水饱和度及气柱高度的数学模型,从而确定气水过渡带和产气界面,因为使用的参数主要为岩心试验数据和测井参数,所以限制条件少。笔者通过对取自4个低渗透气田的729块岩心的压汞毛细管压力曲线、相渗曲线进行分析,建立了渗透率与束缚水饱和度的函数关系,并利用油层物理方法,根据岩心渗透率对202块岩心毛细管压力曲线进行分类和归一化处理[9],得到了气柱高度与毛细管压力、含气饱和度的计算关系式,最后推导出产气界面深度的计算模型。
1 束缚水饱和度的确定利用束缚水饱和度分析储层是否含有可动水,是判断储层流体的一种重要方法[7]。目前计算束缚水饱和度的方法较多,其中岩心试验法的效果较好[9-10]。研究表明,束缚水饱和度与储层的孔渗相关性好[11],选取平均渗透率为0.62~6.00 mD的4个常规低渗透气田的729块岩心(A气田557块岩心,渗透率为0.05~5.00 mD,平均渗透率为0.62 mD,孔隙度为3.6%~11.3%,平均孔隙度6.8%;B气田51块岩心,渗透率为0.002~121.000 mD,平均渗透率为2.000 mD,孔隙度为2.1%~22.0%,平均孔隙度8.9%;C气田60块岩心,渗透率为0.01~99.00 mD,平均渗透率为1.10 mD,孔隙度为3.3%~19.0%,平均孔隙度7.6%;D气田61块岩心,渗透率为0.07~60.00 mD,平均渗透率为6.00 mD,孔隙度为3.9%~16.0%,平均孔隙度8.9%),分析压汞毛细管压力曲线和相渗曲线试验结果,通过回归渗透率与束缚水饱和度的相关关系,建立了渗透率与束缚水饱和度的函数关系(由于C气田中储层泥质含量高达15%以上,并且伴随微裂缝发育,岩心试验的规律与其他3个气田不同,因此在回归渗透率与束缚水饱和度关系时,未采用C气田的岩心数据),结果见图 1。由于采用不同气田的岩心数据进行统计分析,渗透率与束缚水饱和度的相关系数较高,因此可以广泛应用于常规低渗透气田。
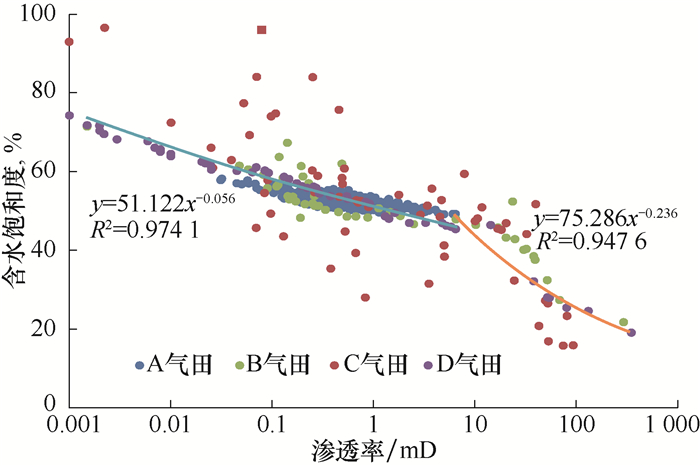
|
| 图 1 通过岩心试验建立的束缚水饱和度与渗透率关系曲线 Fig.1 Correlation between saturation and permeability of irreducible water established through experiments |
根据A,B,D等3个气田的岩心试验数据统计结果,分段回归出束缚水饱和度的计算公式为:
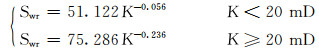
|
(1) |
式中:Swr为束缚水饱和度,%;K为储层渗透率,mD。
选取上述4个气田中12口气井的测井解释参数和测试结论对式(1)的准确性进行验证,结果见图 2。其中,产气不产水的有T12井、C3井和D2井,气水同产井有B3井、A1井、A2井、A3井、A4井、A5井和D3井,产水且有微量产气的井有B2H7井和C1井。
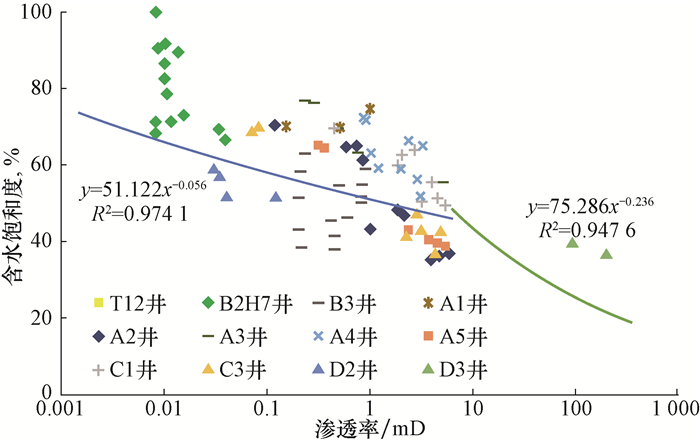
|
| 图 2 12口气井的测井解释结果与束缚水饱和度曲线 Fig.2 Well logging data and irreducible water saturation curves from 12 gas wells |
从图 2可以看出:位于束缚水饱和度曲线以上各点,明显存在可动水,除C3井以外(分析认为,其主要原因是位于束缚水饱和度线以上的2个点物性较差,同时所在的小层厚度小,不到1 m,产出水量少),所有的产水产气井以束缚水饱和度曲线为明显的分界线。这表明采用根据压汞毛细管压力曲线和相渗曲线综合得出的束缚水饱和度能够准确判断流体类型,准确率在92%以上。
2 气柱高度计算方法的建立毛细管压力在油气运移中起到至关重要的作用,是油气二次运移的主要动力,影响储层成藏后的含气饱和度[12-13]。储层被气体充注之前饱和水,当非润湿相的烃类气体形成连续气柱并达到一定高度后,所受浮力大于岩石的排驱压力,天然气将驱替出岩石孔隙中的水[13]。伴随着气柱高度的增加,气柱所受浮力变大,能克服更大的毛细管压力,气体将充注更小的孔喉半径所连通的空间,即一个气柱高度对应一个孔喉半径,大于该半径的孔喉所连通的岩石孔隙空间被天然气充填,低于该半径则仍被水饱和。因此,低渗透气藏中原始含气饱和度既是储层孔喉结构的函数[13],也是气柱高度的函数。
试验条件下测定岩石毛细管压力与储层条件下的天然气受力过程相似,但试验条件的流体、接触角、表面张力与储层条件不一致。因此,需要将压汞试验中测出的毛细管压力换算为储层条件下的毛细管压力,换算关系式为[13]:
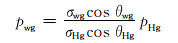
|
(2) |
式中:pwg为气层条件下的毛细管压力,MPa;σwg为气层条件下的气水界面张力,一般取50 mN/m;σHg为试验条件下的界面张力,一般取480 mN/m;θwg为气层条件下的接触角,一般取0°;θHg为试验条件下的接触角,一般取140°;pHg为压汞试验得到的毛细管压力,MPa。
代入各个参数的值,可得:
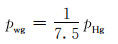
|
(3) |
从式(3)可以看出,压汞试验中测出的毛细管压力pHg是气层条件下毛细管压力pwg的7.5倍。将储层条件下的毛细管压力换算为气柱高度,则得[14]:
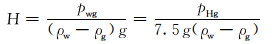
|
(4) |
式中:H为气柱高度,m;ρw为地层水密度,kg/m3;ρg为气层条件下的天然气密度,kg/m3;g为重力加速度,m/s2。
根据流体分析得知,A气田气层条件下ρg=210 kg/m3、ρw=1 010 kg/m3、g=9.8 m/s2,将其代入式(4),可得储层条件下气柱高度和压汞试验测得的毛细管压力之间的关系式为:
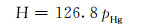
|
(5) |
从式(5)可以看出,压汞试验测出的汞柱压力(毛细管压力)与气柱高度成正比关系。
研究大量的低渗透气藏岩心毛细管压力曲线可知:毛细管压力和含气饱和度在双对数坐标中表现为线性关系[15-16]。对其采用分型理论描述,则毛细管压力与含气饱和度的关系式为[17]:
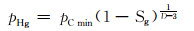
|
(6) |
式中:pC min为排驱压力,即储层最大连通孔隙对应的毛细管压力,MPa;Sg试验中的非润湿相饱和度(与气藏的含气饱和度有关);D为分形维数,取值2~3。
将式(5)代入式(6),即可获得气柱高度和含气饱和度的关系式:
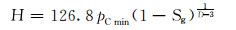
|
(7) |
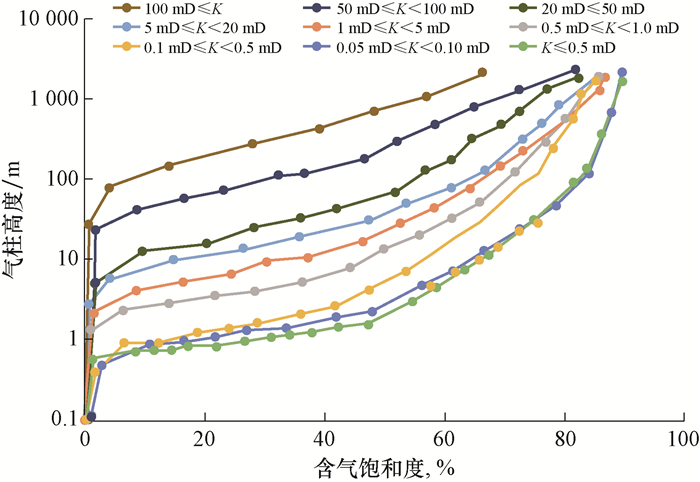
统计A,B,C和D等4个气田202组岩心压汞试验测出的毛细管压力曲线,同时根据这些岩心渗透率的大小将毛细管压力曲线分为9个物性段,在每一物性段的毛细管压力曲线中求取各组曲线的平均pC min和D[17],进而根据式(7)绘制出不同储层条件下含气饱和度与气柱高度的关系图版(见图 3)。
|
| 图 3 不同储层条件下含气饱和度与气柱高度的关系图版 Fig.3 Correlation between gas saturation and gas column height under different reservoir conditions |
从图 3可以看出,不同渗透率储层含气饱和度所对应的气柱高度(气水过渡带的范围)不同。当渗透率低于0.1 mD时,相同含气饱和度对应的气柱高度相近,主要是由于渗透率较低时,储层所对应的毛细管压力相近;当渗透率高于0.1 mD时,相同含气饱和度对应的气柱高度差异较大;同时由于渗透率的不同,束缚水饱和度存在差异,与束缚水饱和度相对应的气柱高度差异更大。物性越好,构造对含气性的影响越显著;同一储层同一深度,物性越好,含气性越好。D气田物性统计得出,其主要层位渗透率低于0.3 mD, 对应的含气饱和度低于32%,结合图 3可知,该气田对应的气柱高度小于3 m。
3 产气界面的确定根据岩心毛细管压力试验结果,可确定出不同物性对应的气柱高度分布图。在此基础上,根据9个物性段含气饱和度与气柱高度的关系,结合单井测井解释的渗透率K和含气饱和度Sg来计算产气界面。公式中使用测井渗透率时需要采用岩心试验校正,根据测井解释的物性和含气饱和度,结合式(7)计算出对应的气柱高度H1:
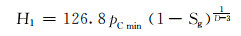
|
(8) |
然后根据式(1)计算出该井对应的束缚水饱和度,进而计算出该束缚水饱和度对应的气柱高度H2:
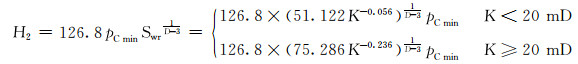
|
(9) |
结合式(8)和式(9)推导出最终的产气界面深度的计算公式为:
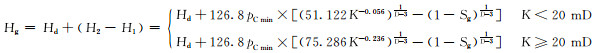
|
(10) |
式中:Hg为产气界面深度,m;Hd为解释层中部深度,m;H1为解释层含气饱和度对应的气柱高度,m;H2为束缚水饱和度对应的气柱高度,m。
从式(10)可以看出:当束缚水饱和度大于测井解释含水饱和度时,产气界面与储层排驱压力呈现线性递减的关系,与分形维数呈现单调降函数关系;反之,产气界面与排驱压力为线性递增的关系,与分形维数呈现单调升函数关系;渗透率与产气界面呈现幂函数关系,当渗透率K≤1 mD时为单调降,当渗透率K>1 mD时为单调增;含气饱和度与产气界面呈现单调降的幂函数关系。
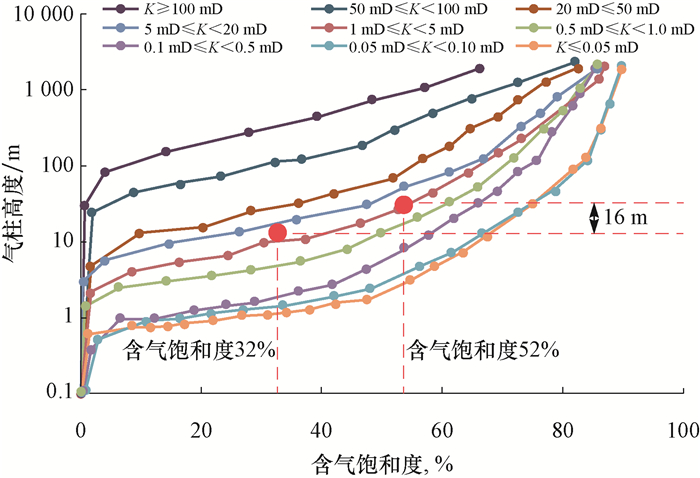
4 应用实例A气田A1井S层深度3 394.60~3 400.30 m,解释渗透率为3.2 mD,含水饱和度68%。根据该层解释的渗透率,用式(1)计算出束缚水饱和度为48%,即含气饱和度大于52%时储层产气,而含气饱和度为52%时,对应的气柱高度H2约为20 m;对照图 3,结合测井解释的含水饱和度为68%,对应的含气饱和度为32%,在该饱和度下气柱高度H1约为4 m;储层中部深度Hd为3 397.45 m;采用式(10)计算出该井S层的产气界面深度为3 413.45 m,推测产气界面高于解释层16 m (见图 4)。
|
| 图 4 A1井产气界面分析结果 Fig.4 Analysis for the gas production interface in Well A1 |
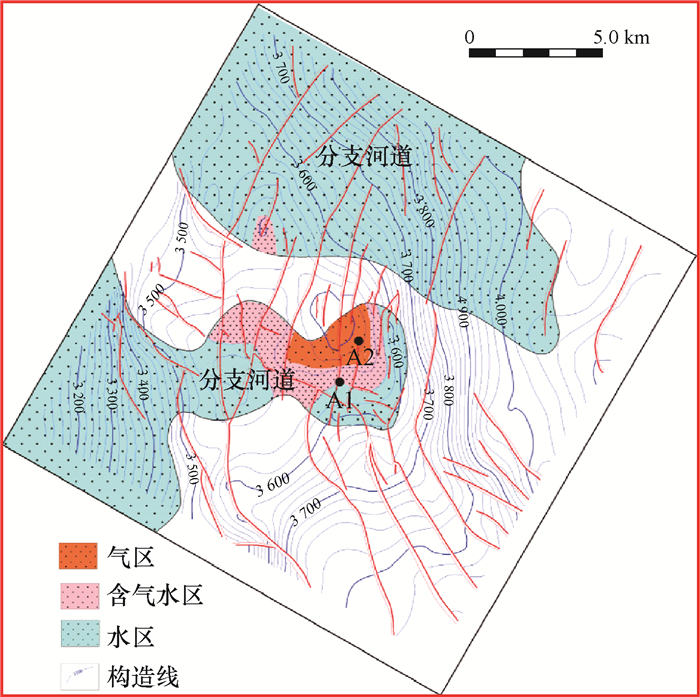
根据上面计算出的A1井S层产气界面深度3 413.45 m,在砂体展布和构造研究成果(见图 5)中绘制出其构造线,该构造线内的面积为产气不产水区域,圈出产气区面积为0.6 km2。位于产气区外的A1井压裂后产气量为0.23×104 m3/d,产水量为29 m3/d;后期在圈定的产气区内新钻A2井,压裂后测试产气量为4.3×104 m3/d,不产水。通过对比产气区内外气井的测试情况得出:位于产气区内的气井压裂后只产气不产水,位于产气界面外的气井压裂后气水同产,表明产气界面深度计算准确。
|
| 图 5 A气田A1井S层气水平面分布 Fig.5 Horizontal distribution of gas and water in formation S of Gas Field A of Well A drill through |
1)产气界面主要受储层渗透率、排驱压力、含气饱和度和分形维数影响,其中渗透率影响最显著,渗透率越高,气柱高度差越大。
2)利用压汞毛细管压力曲线和相渗曲线综合得出的束缚水饱和度,结合测井解释原始含水饱和度,能够准确判断储层流体类型;通过统计分析不同气田的低渗透岩心试验数据可知,泥质含量低于15%的常规低渗透储层的渗透率和束缚水饱和度相关性高,可以根据统计区域束缚水饱和度的试验结果,建立束缚水饱和度与渗透率的计算模型。
3)毛细管压力是影响储层含气饱和度的一个重要因素,分析表明:物性越好,构造对含气性的影响越显著;同一储层同一高度,物性越好,气柱高度越高,含气性越好。
4)根据文中建立的气柱高度与含气饱和度关系图版和计算公式,可以准确计算产气界面的深度和面积,应用实例表明,产气界面的计算模型具有较好的准确性。
| [1] |
罗兴平, 张大勇, 王燕, 等.
MDT单压力点确定油/气/水界面方法[J]. 测井技术 , 2011, 35 (2) : 180–182.
LUO Xingping, ZHANG Dayong, WANG Yan, et al. A method of determining oil/gas/water interface by MDT single pressure data point[J]. Well Logging Technology , 2011, 35 (2) : 180–182. |
| [2] |
伍藏原, 陈文龙.
利用试井数据确定凝析气藏气水界面位置[J]. 油气井测试 , 2004, 13 (3) : 16–17.
WU Zangyuan, CHEN Wenlong. Determining depth of gas and water interface in condensate gas reservoir using test data[J]. Well Testing , 2004, 13 (3) : 16–17. |
| [3] |
丁铃.
确定气水界面的新方法[J]. 油气井测试 , 2007, 16 (3) : 28–30.
DING Ling. A new way to determine gas and water interface[J]. Well Testing , 2007, 16 (3) : 28–30. |
| [4] |
李成, 孙来喜, 袁京素, 等.
低渗透气藏气水界面预测新方法[J]. 钻采工艺 , 2009, 32 (3) : 60–62.
LI Cheng, SUN Laixi, YUAN Jingsu, et al. A new prediction method of gas/water interface in low permeability gas reservoir[J]. Drilling & Production Technology , 2009, 32 (3) : 60–62. |
| [5] |
华锐湘, 贾英兰, 李清, 等.
涩北气田气水分布及气水运动规律分析[J]. 天然气工业 , 2009, 29 (7) : 68–71.
HUA Ruixiang, JIA Yinglan, LI Qing, et al. An analysis of gas-water distribution and its movement law in the Sebei Gas Field[J]. Natural Gas Industry , 2009, 29 (7) : 68–71. |
| [6] |
李爱国, 易海永, 涂建斌, 等.
压力交会法确定ZG气田石炭系气藏气水界面[J]. 天然气工业 , 2005, 25 (supplement A) : 35–37.
LI Aiguo, YI Haiyong, TU Jianbin, et al. Determining the gas-water interface of carboniferous gas reservoir in ZG Field by pressure intersection method[J]. Natural Gas Industry , 2005, 25 (supplement A) : 35–37. |
| [7] |
华永川.
川东北飞仙关组鲕滩气藏气水界面预测方法[J]. 天然气工业 , 2004, 24 (8) : 76–77.
HUA Yongchuan. Prediction method of gas-water interface for oolitic beach reservoir of Feixianguan Group in Northeast Sichuan[J]. Natural Gas Industry , 2004, 24 (8) : 76–77. |
| [8] |
何更生.
油层物理[M]. 北京: 石油工业出版社 ,1994 : 80 -86.
HE Gengsheng. Reservoir physics[M]. Beijing: Petroleum Industry Press , 1994 : 80 -86. |
| [9] |
刘子雄.
低渗气藏可动水识别方法研究[J]. 石油地质与工程 , 2016, 30 (2) : 93–95.
LIU Zixiong. Movable water recognition method research of low permeability gas reservoir[J]. Petroleum Geology and Engineering , 2016, 30 (2) : 93–95. |
| [10] |
邢会民.
基于常规测井资料的束缚水饱和度综合确定方法研究[J]. 钻采工艺 , 2010, 33 (supplement 1) : 37–40.
XING Huimin. Comprehensive determination method study on the irreducible water saturation based on the routine logging data[J]. Drilling & Production Technology , 2010, 33 (supplement 1) : 37–40. |
| [11] |
高华, 高楚桥, 胡向阳.
莺歌海盆地束缚水饱和度影响因素研究[J]. 石油物探 , 2005, 44 (2) : 158–159.
GAO Hua, GAO Chuqiao, HU Xiangyang. Influential factors of irreducible water saturation in Yinggehai[J]. Geophysical Prospecting for Petroleum , 2005, 44 (2) : 158–159. |
| [12] |
成志刚, 王黎.
利用NMR资料建立束缚水解释模型[J]. 江汉石油学院学报 , 2003, 25 (2) : 66–67.
CHENG Zhigang, WANG Li. Establishment of bound water interpreting model with nuclear magnetic resonance (NMR) data[J]. Journal of Jianghan Petroleum Institute , 2003, 25 (2) : 66–67. |
| [13] |
金燕.
测井模糊聚类法在复杂碳酸盐岩气藏含气面积圈定中的应用[J]. 天然气工业 , 1997, 17 (2) : 24–27.
JIN Yan. Application of logging fuzzy clustering procedure in delimitating the gas bearing area of complex carbonate reservoirs[J]. Natural Gas Industry , 1997, 17 (2) : 24–27. |
| [14] |
李宁, 周克明, 张清秀, 等.
束缚水饱和度实验研究[J]. 天然气工业 , 2002, 22 (supplement 1) : 110–113.
LI Ning, ZHOU Keming, ZHANG Qingxiu, et al. Experimental research on irreducible water saturation[J]. Natural Gas Industry , 2002, 22 (supplement 1) : 110–113. |
| [15] |
邸世祥.
碎屑岩储集层的孔隙结构及其成因与对油气运移的控制作用[M]. 西安: 西北大学出版社 ,1991 : 50 -56.
DI Shixiang. Pore structure clastic reservoir and its control on hydrocarbon migration[M]. Xi'an: Northwestern University Press , 1991 : 50 -56. |
| [16] |
廖明光, 李士伦, 谈德辉.
砂岩储层渗透率与压汞曲线特征参数间的关系[J]. 西南石油学院学报 , 2001, 23 (4) : 5–8.
LIAO Mingguang, LI Shilun, TAN Dehui. Relationship between permeability and mercury injection parameters curve for sandstone reservoir[J]. Journal of Southwest Petroleum Institute , 2001, 23 (4) : 5–8. |
| [17] |
杨宇, 周文, 林璠, 等.
一种新的致密气藏平均毛管压力计算模型[J]. 成都理工大学学报(自然科学版) , 2014, 41 (6) : 768–772.
YANG Yu, ZHOU Wen, LIN Fan, et al. A new method for computing average capillary pressure curve of tight gas reservoir[J]. Journal of Chengdu University of Technology (Science & Technology Edition) , 2014, 41 (6) : 768–772. |




