2. 中国石化石油工程技术研究院, 北京 100101 ;
3. 中国石油大学(北京)石油工程学院, 北京 102249
2. Sinopec Research Institute of Petroleum Engineering, Beijing, 100101 ;
3. College of Petroleum Engineering, China University of Petroleum(Beijing), Beijing, 102249, China
水平井固井时,由于重力作用的影响,水泥浆顶替隔离液的机理较直井要复杂得多,顶替效率与固井质量一般也难以保证。为此,国内外学者对水平井顶替机理与规律进行了大量研究,取得了不少成果[1-8],使水平井固井技术得到很大提高,但是由于井下条件复杂,受物理模拟试验与测试水平的制约,对水平井顶替界面的发展规律还没形成系统的理论认识。近几十年来,计算流体力学与计算机技术的迅速发展,为水平井偏心环空顶替机理的研究提供了有效的手段[9-10]。笔者在前人研究的基础上,根据顶替作业时流体流动的特点,考虑顶替界面的质量扩散效应[11]和流态耦合效应[12],建立了水平井顶替作业时流体流动的数学模型,并利用FIUENT软件进行了系统的数值模拟试验,分别考察了偏心度和密度差耦合条件下水泥浆顶替隔离液的界面形态变化过程,得到了界面特征和顶替效率变化规律,为水平井顶替作业时降低掺混段长度、提高顶替效率与固井质量提供了理论依据。
1 数值模拟模型的建立水平井固井水泥浆顶替隔离液过程中,水泥浆与隔离液之间属于细长体条件下的液液两相流动,不仅在两相之间存在质量扩散,而且在偏心环空的宽窄边存在紊流与层流的流态差异,需采用合理的数学模型进行描述。
1.1 物理模型与网格划分利用Gambit软件建立水平井固井顶替作业的三维物理模型,钻头直径为215.9 mm,井径扩大率以8%计算,则物理模型的井眼直径为233.2 mm,套管外径为139.7 mm,设置计算长度为50 m,套管偏心度为0.1,0.3,0.5和0.7,忽略井眼不规则与不同偏心度下扶正器所占空间对流体流动的影响,采用半环空两侧对称几何结构,如图 1所示。

|
| 图 1水平井偏心环空模型 Fig.1Horizontal well eccentric annulus model |
选用六面体结构网格对规则的水平井偏心环空模型进行网络划分,50 m长环空模型离散网格数量为120万,为了保证计算精度,对壁面进行网格加密处理。物理模型的网格划分如图 2所示。

|
| 图 2水平井偏心环空的网格划分 Fig.2Horizontal well eccentric annulus meshing |
水平井固井顶替过程为非牛顿流体在偏心环空中的液液两相流动,流动规律可用流体力学方程组描述 。
不可压缩流体的连续性方程为:
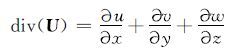
|
(1) |
式中:U为速度,m/s;u,v和w分别为x,y和z方向上的分速度,m/s。
不可压缩流体的动量方程为:
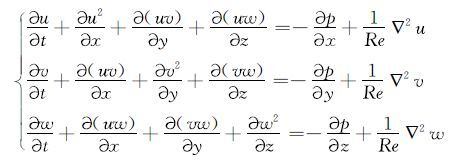
|
(2) |
式中:p为压力,Pa;Re为雷诺数。
流态由FLUENT软件来自动识别,湍流部分的计算采用标准k-ε模型的控制方程[13]:
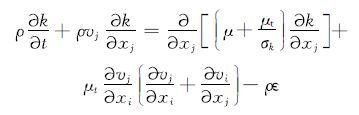
|
(3) |

|
(4) |
式中:μ为流体动力黏度,Pa·s;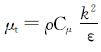
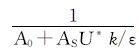
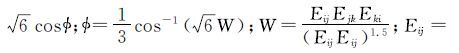

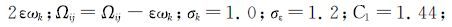
为真实描述两相流体间的掺混现象,设定组分模型来描述两相顶替流动过程,利用物质输运方程、层流和紊流中的扩散方程来描述流体间的质量扩散问题[11],通过求解第i组分的对流扩散方程来计算每个组元的质量分数Yi。质量守恒方程为:
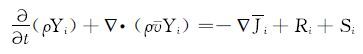
|
(5) |
式中:Ri为第i组分在化学反应中的净生成速率,mol/(L·s);Si为扩散项加上源项而成的净生成速率,mol/(L·s);Ji为存在浓度梯度情况下第i组分所产生的扩散流量,m3/s,对于层流流动,i=-ρDi,m∇Yi,Di,m为第i组分的扩散系数;对于湍流,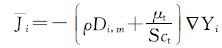
在经过计算得到单元网格内各组分的质量分数和体积分数后,每一个单元网格的密度采用网格内各组分体积分数加权法得到,每一个单元网格的黏度采用网格内各组分质量分数加权法得到。
水平井偏心环空顶替流场包括入口边界、出口边界、环空内外壁面边界以及对称边界[14],其边界条件如下:
1) 入口边界条件。采用速度入口边界条件,在入口位置直接对法向速度赋值。
2) 出口边界条件。采用质量出口边界,利用相邻内部流场节点数据计算,以满足质量守恒条件。
3) 对称边界条件。在水平井偏心环空左右两侧采用对称边界条件以降低计算量。
4) 壁面边界条件。在套管壁面和井筒壁面上,采用无滑移壁面边界条件。
2 数值模拟试验及分析水泥浆顶替隔离液为正密度差条件下高黏流体之间的液液两相流动,在宽窄边效应、重力作用、质量扩散等多种因素耦合影响下,表现出特有的顶替界面特征。笔者通过算例分析水平段偏心环空固井顶替流动特征。基本参数:井眼直径215.9 mm;套管直径139.7 mm;水泥浆密度1.90 kg/L,流性指数0.7,稠度系数0.5;隔离液流性指数0.8,稠度系数0.2;排量1.2 m3/min;隔离液密度1.50,1.70和1.85 kg/L;偏心度为0.1,0.3,0.5和0.7。
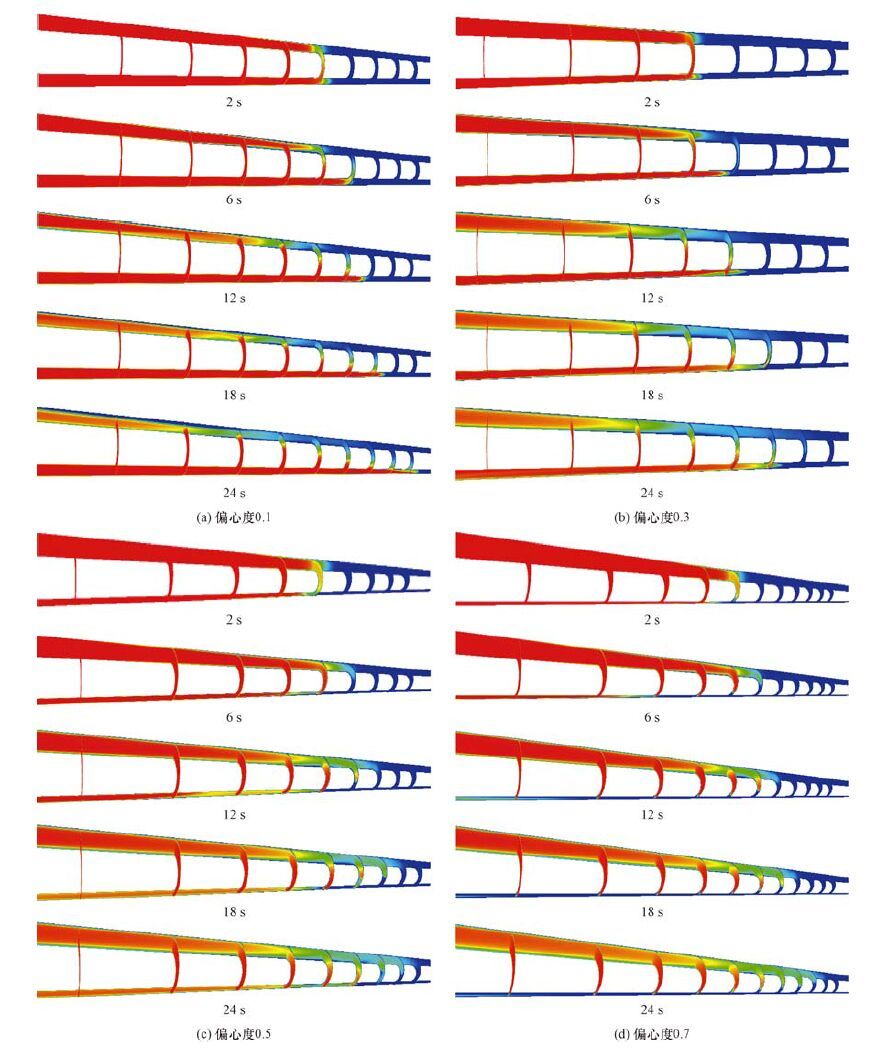
2.1 偏心度与密度差耦合对界面形态的影响图 3为密度差0.20 kg/L条件下,不同偏心度下顶替界面随顶替时间变化的发展过程,图中红色代表水泥浆,蓝色代表隔离液。定义水泥浆体积分数80%的位置为顶替后缘,水泥浆体积分数20%的位置为顶替前缘,界面长度为顶替前缘位置与顶替后缘位置的距离。
|
| 图 3不同偏心度下顶替界面随顶替时间的变化过程 Fig.3The changes of displacement interface over displacement time under different eccentricity |
水平段偏心环空内正密度差顶替过程中主要存在3种特殊效应:1)由偏心度引起的偏心效应,使环空间隙出现宽边和窄边,宽边侧的流体流动阻力小,流速大,窄边侧的流体流动摩阻较大,流速较慢;2)由密度差引起的浮力效应,2种密度不同的流体相互掺混后,密度较大的流体受到竖直向下的合力,密度较小的流体受到竖直向上的合力,使两相流体交界面产生分层流动趋势;3)由对流引起的质量扩散效应,在两相流体交界面上流体质点相互接触掺混,随着时间推移交界面转变为一个持续增厚的过渡带,在这个过渡带内两相流体因扩散效应而持续充分掺混,使过渡带内混合流体的密度趋于一致且有别于顶替液和被顶替液的密度。这3种效应同时存在,相互作用,其中偏心效应和浮力效应对顶替界面形态的影响最强。
由图 3可以看出:1)偏心效应弱于浮力效应时(如偏心度为0.1时),低边水泥浆流动不断超前,形成低边指进的分层流,顶替界面长度随着顶替时间推移持续增长,受质量扩散效应影响,过渡带随时间推移明显增厚增长;2)偏心效应强于浮力效应时(如偏心度为0.7时),高边水泥浆流动不断超前,形成高边指进的分层流,顶替界面长度随着顶替时间推移持续增长。受质量扩散效应影响,过渡带随时间推移明显增厚增长;3)当偏心效应与浮力效应基本相当时(如偏心度为0.3),窄边略有指进,顶替界面形态变化趋于稳定,顶替界面长度随着顶替时间增长变化不大。受质量扩散效应影响,过渡带随时间推移明显增厚增长。
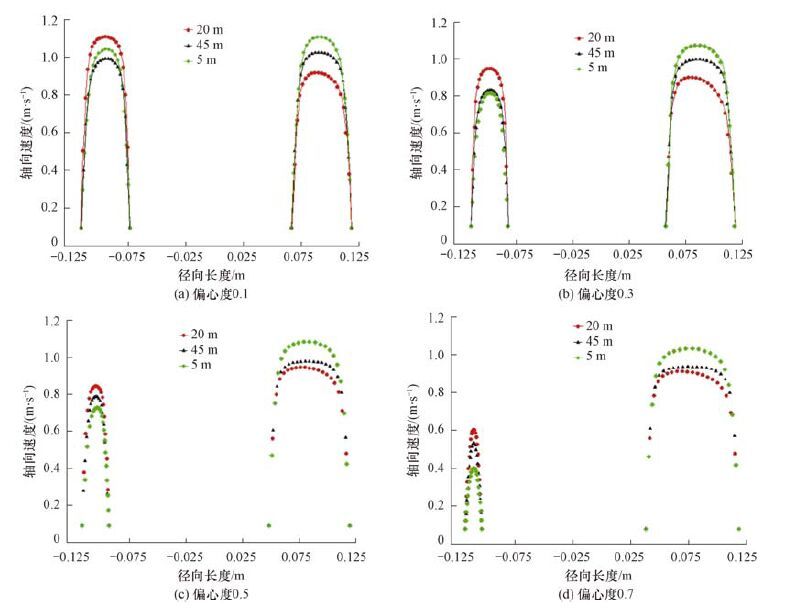
为了揭示高边指进和低边指进的形成机理,对距入口不同位置处的轴向速度剖面进行了分析。图 4为距入口5,20和45 m处不同偏心环空速度分布特征,图中左侧为环空低边轴向速度分布,右侧为环空高边轴向速度分布。距入口5 m和45 m处分别为水泥浆和隔离液,距入口20 m处为顶替界面中部。由图 4可以看出:低偏心度(偏心度为0.1和0.3)时,偏心效应小于浮力效应,距入口5 m和45 m处的单相流动区域内,环空高边流速略大于低边;距入口20 m处的分层界面区域内,环空低边流速大于高边流速,这种速度差导致顶替界面出现低边指进的分层流动特征,由于为正密度差顶替,水泥浆从高边向低边滑落,降低了高边顶替速度,补充了低边流量,使低边的顶替速度得到提高,同时也提高了低边壁面的切应力,这有助于提高环空低边的顶替效率。高偏心度(偏心度为0.5和0.7)时,偏心效应大于浮力效应,距入口5 m和45 m处的单相流动区域内,环空高边流速明显大于低边;距入口20 m处的分层界面区域内,环空低边没有得到高边流量的补充,低边流速小于高边流速,这种速度差导致顶替界面出现高边指进的分层流动特征。
|
| 图 4不同偏心度下环空流速剖面 Fig.4The annulus velocity profile under different eccentricity |
由图 3和图 4可以看出:随着偏心度持续增大,顶替界面从低边指进转变为高边指进,因此必然存在某一特定的偏心度,使偏心效应和浮力效应对界面形态的影响相对平衡,顶替界面形态趋于稳定且界面长度相对最短,这一稳定的界面形态是固井施工过程中追求的最佳界面形态,此时顶替效率也最高。
质量扩散效应在整个顶替过程中一直起作用,从顶替流动的特征看,对流掺混起主导作用,因此在偏心效应和浮力效应未达到平衡状态而呈现典型的高边或者低边指进时,界面长度持续明显增长,使重力方向上的对流扩散接触面积不断增大,从而增大了重力方向上的对流扩散规模,宏观上表现为过渡带持续增厚变宽和密度趋于均一。当偏心效应和浮力效应达到平衡状态时,界面长度相对稳定,重力方向上的对流扩散接触面积增大趋势得到抑制,扩散规模相对稳定,宏观上表现为过渡带略有增厚。
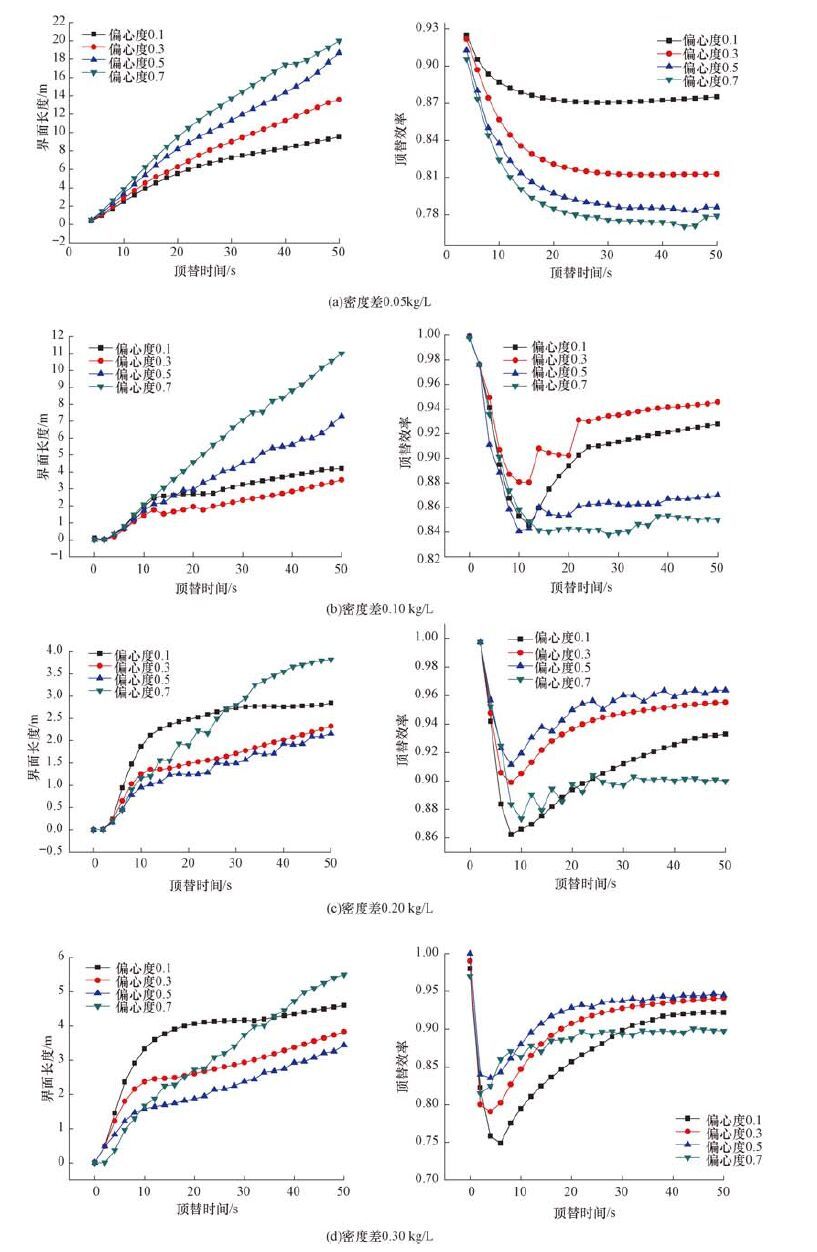
2.2 偏心度与密度差耦合对顶替界面特征的影响根据不同套管偏心度的固井顶替数值模拟结果,绘制不同套管偏心度条件下顶替界面长度和顶替效率随顶替时间的变化曲线,结果如图 5所示。
|
| 图 5偏心度与密度差耦合对顶替界面特征的影响 Fig.5Effect of coupled eccentricity and density difference on displacement interface feature |
由图 5可以看出:
1) 密度差为0.05 kg/L时,随着偏心度增大,界面长度增长,顶替效率降低,因此当密度差较小时,应提高套管居中度,以降低顶替界面长度,提高顶替效率。
2) 密度差为0.10 kg/L时,偏心度约为0.3时,偏心效应和浮力效应趋于平衡,顶替界面相对稳定,顶替效率最高;当偏心度继续增大时,界面长度增长,顶替效率降低。因此,在文中计算条件下,固井施工参数与文中模拟参数基本一致的情况下,降低水平段套管偏心度,控制偏心度不大于0.3,有利于降低顶替界面长度,提高顶替效率。
3) 密度差为0.20和0.30 kg/L时,偏心度为0.5时,界面长度最短,顶替效率最高,当偏心度较小(e=0.1)和较大(e=0.7)时,界面长度均较大,顶替效率都相对偏低。
3 结 论1) 针对水平井偏心环空顶替问题,运用物质输运模型描述两相流体之间的质量扩散与流态识别,建立了更接近实际工况的水平井三维偏心环空动态顶替数学模型,为研究水平井固井顶替提供了一种有效的手段。
2) 顶替界面形态主要受偏心效应、浮力效应及质量扩散效应的影响。偏心度增大,偏心效应增强,顶替界面高边指进趋势增强;正密度差增大,浮力效应增强,顶替界面低边指进趋势增强。当2种效应达到临界平衡状态时,两相顶替界面形态就达到一种临界稳定状态,此时顶替界面形态相对稳定且界面长度无明显增长,顶替效率最高,这是水平井固井顶替施工所要追求的最佳界面状态。
3) 质量扩散效应主要以对流掺混的方式在整个顶替过程中一直起作用,在轴向对流扩散的同时也存在重力方向上的对流扩散。顶替界面的界面长度越长,重力方向的对流扩散接触面积越大,重力方向上的对流扩散规模越大,过渡带越厚,因此水平井固井施工时,应使顶替界面形态相对稳定,以缩短混浆段长度。
4) 当密度差较小时,降低套管偏心度,有利于降低界面长度,提高固井顶替效率;当密度差较大时,套管适度偏心反而有助于获得稳定的顶替界面和较高的顶替效率。
| [1] | 陈家琅, 黄匡道, 刘永建, 等. 定向井固井注水泥顶替效率研究[J]. 石油学报 , 1990, 11 (3) : 98–105. CHEN Jialang, HUANG Kuangdao, LIU Yongjian, et al. Displacement efficiency of cementing in directional wells[J]. Acta Petrolei Sinica , 1990, 11 (3) : 98–105. |
| [2] | 万发明, 吴广兴, 高大勇. 小井眼固井顶替效率研究[J]. 石油学报 , 2000, 21 (5) : 72–76. WAN Faming, WU Guangxing, GAO Dayong. Experimental investigation on cementing displacement efficiency of slimhole well[J]. Acta Petrolei Sinica , 2000, 21 (5) : 72–76. |
| [3] | 丁士东, 张卫东. 国内外防气窜固井技术[J]. 石油钻探技术 , 2002, 30 (5) : 35–38. DING Shidong, ZHANG Weidong. Domestic&oversea cementing techniques of gas-channeling prevention[J]. Petroleum Drilling Techniques , 2002, 30 (5) : 35–38. |
| [4] | 丁士东. 塔河油田紊流、塞流复合顶替固井技术[J]. 石油钻采工艺 , 2002, 24 (1) : 20–22. DING Shidong. Combination displacement cementing of turbulent and plug flow in Tahe Oilfield[J]. Oil Drilling&Production Technology , 2002, 24 (1) : 20–22. |
| [5] | 李早元, 杨绪华, 郭小阳, 等. 固井前钻井液地面调整及前置液紊流低返速顶替固井技术[J]. 天然气工业 , 2005, 25 (1) : 93–95. LI Zaoyuan, YANG Xuhua, GUO Xiaoyang, et al. Cementing techniques of ground adjusting drilling fluid properties before cementing and displacing mud by turbulent pre-flush at low return velocity[J]. Natural Gas Industry , 2005, 25 (1) : 93–95. |
| [6] | 李洪乾. 螺旋套管扶正器诱导环空流场的数值模拟[J]. 石油钻探技术 , 2012, 40 (2) : 25–29. LI Hongqian. Numerical simulation on the annular flow induced by spiral casing centralizer[J]. Petroleum Drilling Techniques , 2012, 40 (2) : 25–29. |
| [7] | 舒秋贵. 油气井固井注水泥顶替理论与技术综述[J]. 西部探矿工程 , 2005, 17 (12) : 85–87. SHU Qiugui. Review on oil and gas well cementing displacement theory and technology[J]. West-China Exploration Engineering , 2005, 17 (12) : 85–87. |
| [8] | 王少平, 曾扬兵, 沈孟育, 等. 用RNG k-ε模式数值模拟180°弯道内的湍流分离流动[J]. 力学学报 , 1996, 28 (3) : 257–263. WANG Shaoping, ZENG Yangbing, SHEN Mengyu, et al. Numerical calculation of turbulent separated flows in 180 deg duct with RNG k-ε turbulence model[J]. Acta Mechanica Sinica , 1996, 28 (3) : 257–263. |
| [9] | 王斌斌, 王瑞和, 步玉环. 不同流态下水泥浆环空顶替的数值模拟研究[J]. 钻井液与完井液 , 2010, 27 (3) : 76–78. WANG Binbin, WANG Ruihe, BU Yuhuan. Numerical simulation on cementing displacement in different flow patterns[J]. Drilling Fluid&Completion Fluid , 2010, 27 (3) : 76–78. |
| [10] | 张松杰, 薛亮, 汪志明, 等. 密度差对水平井固井顶替影响规律数值模拟研究[J]. 钻采工艺 , 2012, 35 (6) : 15–17. ZHANG Songjie, XUE Liang, WANG Zhiming, et al. Numerical simulation study on the influence law of density difference on cementing displacement interface in the horizontal well[J]. Drilling&Production Technology , 2012, 35 (6) : 15–17. |
| [11] | 温正, 石良辰, 任毅如. FLUENT流体计算应用教程[M]. 北京: 清华大学出版社 ,2009 : 81 -82. WEN Zheng, SHI Liangchen, REN Yiru. FLUENT fluid computing applications tutorial[M]. Beijing: Tsinghua University Press , 2009 : 81 -82. |
| [12] | MENTER F R, LANGTRY R B, LIKKI S R, et al. A correlation-based transition model using local variables:part 1:model formulation[J]. Journal of Turbomachinery , 2006, 128 (3) : 413–422. DOI:10.1115/1.2184352 |
| [13] | 汪志明, 崔海清, 何光渝. 流体力学[M]. 北京: 石油工业出版社 ,2006 : 144 -146. WANG Zhiming, CUI Haiqing, HE Guangyu. Fluid mechanics[M]. Beijing: Petroleum Industry Press , 2006 : 144 -146. |
| [14] | 王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社 ,2004 : 210 -211. WANG Fujun. Computational fluid dynamics analysis:software principles and applications of CFD[M]. Beijing: Tsinghua University Press , 2004 : 210 -211. |




