2. 西南石油大学材料科学与工程学院, 四川成都 610500;
3. 中国石油天然气集团公司石油管工程重点实验室(西南石油大学), 四川成都 610500
2. School of Materials and Engineering, Southwest Petroleum University, Chengdu, Sichuan, 610500, China;
3. CNPC Key Lab for Tubular Goods Engineering (Southwest Petroleum University), Chengdu, Sichuan, 610500, China
钻杆在井下承受内外压力、轴向力、弯曲应力和扭应力等多种载荷的联合作用,因此在钻进过程中常常发生失效,尤其容易发生载荷与腐蚀介质联合作用下的疲劳失效[1, 2, 3, 4, 5]。统计数据表明,国内外油田均发生过钻杆疲劳断裂事故[6, 7],造成了巨大的经济损失[8],因此,研究钻杆疲劳性能具有现实意义。而疲劳是一个塑形应变累积的过程,是一种复杂的现象,因此不能通过简单的物理概念来描述疲劳曲线;另外,一切与疲劳曲线有关的参数都不能表征材料的物理性能,只能表征材料的工程性能,因此对钻杆疲劳性能进行试验研究能够指导其在实际工程中的应用[9]。
在进行钻杆强度设计时,一般基于静载条件,并没有考虑疲劳因素的影响。而在动载荷下,钻杆表面形成微裂纹,内部成核,扩展直至钻杆疲劳断裂,因此明确钻杆的疲劳极限可以确保安全钻井。为此,笔者对常用的S135和G105钻杆的疲劳寿命进行了试验研究:在对钻杆进行受力分析的基础上,结合数理统计和安全可靠性理论,计算了可用于实际工程中表征钻杆疲劳性能的应力-疲劳寿命曲线(S表示应力,N表示疲劳寿命,记为S-N曲线);当前对于S-N曲线的研究,主要采用中短寿命区的成组试验法和长寿命区的升降法,鉴于升降法耗费时间久,疲劳试样的加工费用较高,因此采用外推法对试验得到的曲线进行外推延长以得到材料的疲劳极限值,并将常用的2m-1指数外推法(以下简称2m-1外推法)和直接外推法得到的外推值与升降法试验结果进行了对比。
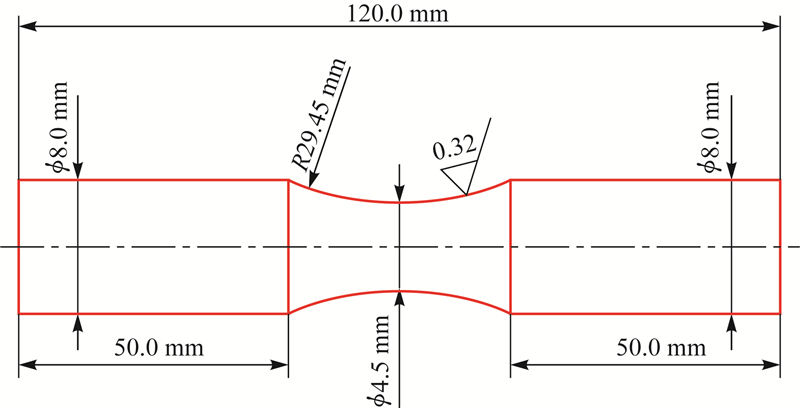
1 试验材料及方法 1.1 试验材料试验所用疲劳试样取自S135和G105钻杆,2种钢级钻杆材料的化学成分见表1,疲劳试样的形状及尺寸如图1所示。试验用PQ-6旋转弯曲疲劳试验机,转速3 000 r/min。根据国家推荐标准《金属材料 疲劳试验 旋转弯曲方法》[10]的规定,试验在室温下进行,试样承受对称循环应力(R=-1)。
| 质量分数,% | |||||||||
| 钻杆钢级 | C | Si | Mn | P | S | Cr | Mo | Ni | Fe |
| S135 | 0.300 | 0.240 | 1.300 | 0.010 | 0.006 | 0.380 | 0.240 | 0.030 | 97.500 |
| G105 | 0.340 | 0.200 | 1.090 | 0.015 | 0.008 | 1.030 | 0.200 | 0.020 | 97.100 |
|
| 图1 钻杆疲劳试样尺寸 Fig.1 Dimension of fatigue test sample of drill pipe |
当应力降至某一极限值时,S-N曲线趋近于水平线,即当应力不超过该极限值时,疲劳寿命可无限增大,该极限值即为材料的疲劳极限。笔者利用升降法预测疲劳极限,以该极限值为依据绘制S-N曲线的水平部分。采用升降法预测疲劳极限时,根据经验公式σ≈0.5σb(σ为第一次加载应力,MPa;σb为材料抗拉强度,MPa)初步估计疲劳极限。一般在预估疲劳极限附近3~5级应力水平下进行试验,应力增量取20 MPa。试样寿命达到1.0×107时记为“越出”,试样寿命小于1.0×107时记为“破断”,试样“破断”或“越出”即停止试验。如果高一级应力水平试样“破断”,则降低应力水平再做一个试样;如果低一级应力水平“越出”,则升高应力水平再做一个试样。完成15个左右的试样后,对试验数据进行配对。将低应力水平σi“越出”的试样与高一级应力水平σi+1“破断”的试样配成一个对子,得到一个疲劳极限数据(σi+σi+1)/2,这样就可以获得一系列疲劳极限数据,其平均值记作S-1,av,标准差记作S-1,rms。
认为疲劳极限服从正态分布[11],则条件疲劳极限S-1,P-C的计算式为:
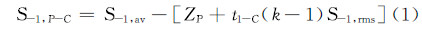
采用成组法测定S-N曲线的中短寿命区曲线。取4~5级较高应力水平,保证各应力水平下试样均“破断”,在各级应力水平下做4~6个试样。认为每级疲劳寿命数据服从对数正态分布,而疲劳应力与疲劳寿命服从Basquin模型:

因此,疲劳S-N曲线可表示为对数疲劳寿命均值和均方差曲线,表达式为:
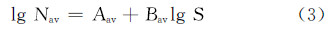
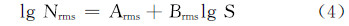
任意存活率P下的S-N曲线可用下式所示模型来表征[12]:
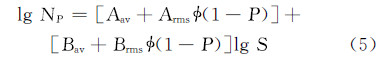
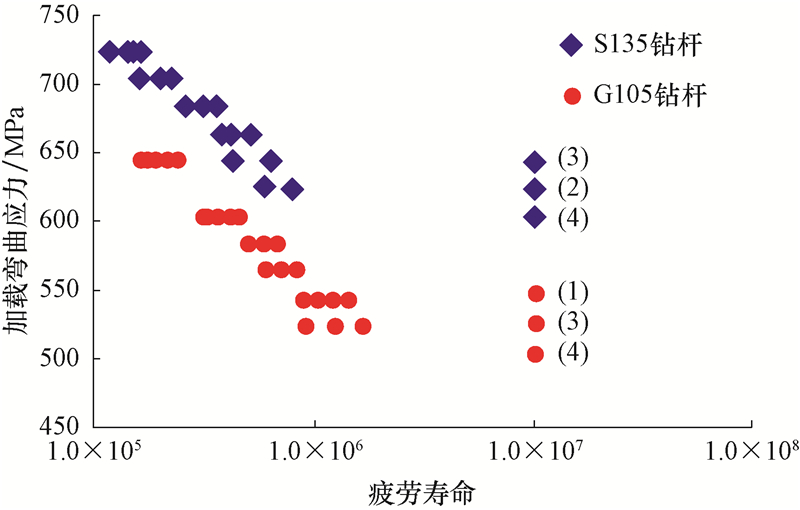
试验所得S135和G105钻杆的疲劳数据如图2所示(括号里的数字表示对应应力下“越出”试样的个数,下同)。
|
| 图2 S135及G105钻杆疲劳试验数据 Fig.2 Fatigue test data of drill pipes S135 and G105 |
将试验得出的升降法的配对数据代入式(5)计算应力疲劳极限,计算得到不同置信度下S135和G105钻杆的疲劳极限(见表2和表3)。
| 存活率,% | 置信度,% | t1-C(6) | 疲劳极限/MPa |
| 50 | 90 | 1.943 2 | 601.49 |
| 95 | 2.446 9 | 592.37 | |
| 99 | 3.707 4 | 569.55 | |
| 90 | 90 | 1.943 2 | 578.32 |
| 95 | 2.446 9 | 569.20 | |
| 99 | 3.707 4 | 546.38 | |
| 99 | 90 | 1.943 2 | 559.31 |
| 95 | 2.446 9 | 550.19 | |
| 99 | 3.707 4 | 527.37 |
| 存活率,% | 置信度,% | t1-C(6) | 疲劳极限/MPa |
| 50 | 90 | 1.943 2 | 497.89 |
| 95 | 2.446 9 | 490.23 | |
| 99 | 3.707 4 | 471.05 | |
| 90 | 90 | 1.943 2 | 478.42 |
| 95 | 2.446 9 | 470.76 | |
| 99 | 3.707 4 | 451.59 | |
| 99 | 90 | 1.943 2 | 462.45 |
| 95 | 2.446 9 | 454.79 | |
| 99 | 3.707 4 | 435.62 |
由表2可知,当置信度为95%时,存活率50%,90%和99%对应的疲劳极限值分别为592.37,569.20和550.19 MPa。
由表3可知,当置信度为95%时,存活率50%,90%和99%对应的疲劳极限值分别为490.23,470.76和454.79 MPa。
按照前述成组法计算S135钻杆在各级试验应力下的疲劳寿命的对数平均值和对数标准差。按照式(3)的形式对对数平均值与对数应力值进行线性拟合,得Aav=51.887 0、Bav=-16.369 0;按照式(4)的形式对对数标准差与对数应力值进行线性拟合,得Arms=0.938 7,Brms=-0.309 1。将Aav,Bav,Arms和Brms的值代入式(5)得S135钻杆中短寿命区的S-N曲线表达式为:
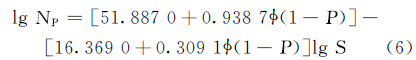
同理,将G105钻杆的疲劳数据进行整理,得出参数Aav,Bav,Arms和Brms的值分别为32.238 2,-9.585 8和1.052 4和-0.358 9。将其代入式(5)得G105钻杆中短寿命区的S-N曲线表达式为:
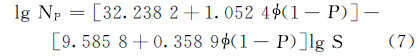
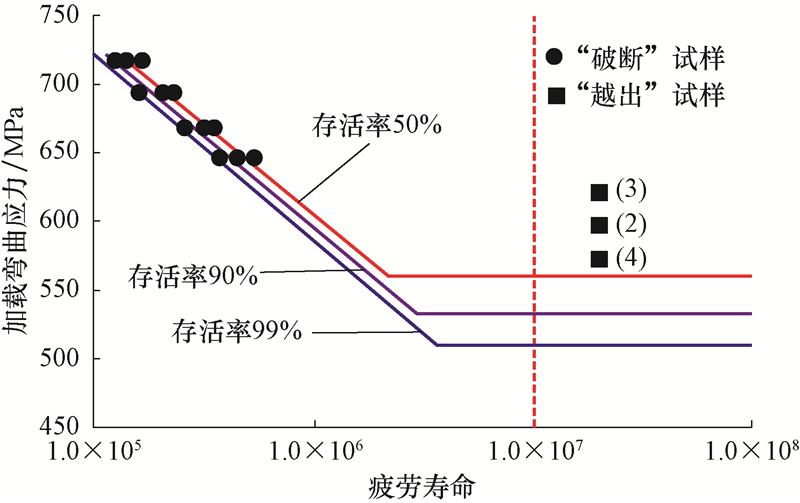
研究存活率为50%,90%和99%时S135钻杆的疲劳寿命,将对应的概率分布函数值分别代入式(6),即可得到S135钻杆在中短寿命区的3条不同存活率的S-N曲线。已知表2中对应这3个存活率下的疲劳极限值(取置信度为95%,下同),以该极限值作为S-N曲线的拐点,将中短寿命区曲线与升降法得到的极限值绘制在同一S-lgN图中,得到S135钻杆完整的S-N曲线(见图3)。
|
| 图3 S135钻杆完整疲劳曲线 Fig.3 S-N curve of drill pipe S135 |
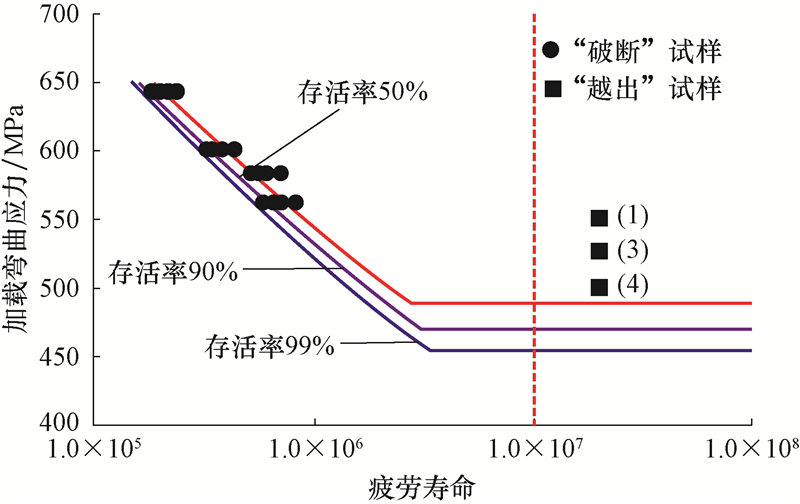
将存活率为50%,90%和99%对应的概率分布函数值代入式(7),计算出G105钻杆中短寿命区3条不同存活率的S-N曲线,将其与升降法得到的疲劳极限值绘制在同一S-lgN图中,得到G105钻杆的S-N曲线(见图4)。
|
| 图4 G105钻杆完整疲劳曲线 Fig.4 S-N curve of drill pipe G105 |
通过旋转弯曲疲劳试验获得长寿命区的试验数据耗时长,费用高,因此设法通过中短寿命区的S-N疲劳寿命曲线外推得到长寿命曲线具有现实意义。
对常见的2m-1外推法和直接外推法进行验证分析,并将二者的外推值与升降法试验值进行对比。利用文献[13]介绍的2m-1外推法,即从N=5.0×106开始,将原先中短寿命S-N曲线的指数m变为2m-1,对长寿命S-N曲线进行外推。根据中短寿命S-N曲线的Aav,Bav,Arms和Brms计算出疲劳寿命为5.0×106对应的疲劳极限St=10[lg(5.0×106)-Aav]/Bav。按照公式Fav=2Bav+1、Eav=Aav-BavlgSt-lgSt、Frms=2Brms、Erms=Arms-BrmslgSt计算出S135钻杆外推曲线的基础参量St,Eav,Fav,Erms和Frms分别为576.216 7,94.314 4,-31.738 0,2.645 2和-0.618 2 MPa;G105钻杆外推曲线的基础参量St,Eav,Fav,Erms和Frms分别为461.615 5,55.113 2,-18.171 6,2.008 6和-0.717 8 MPa。疲劳曲线的长寿命区域即可用外推法得到的参数来表示,选N=1.0×107所对应的应力作为外推疲劳极限值。
直接外推法即将成组法试验结果分析得出的中短寿命区曲线直接应用到长寿命区域,取疲劳寿命为1.0×107时对应的应力作为疲劳极限值。
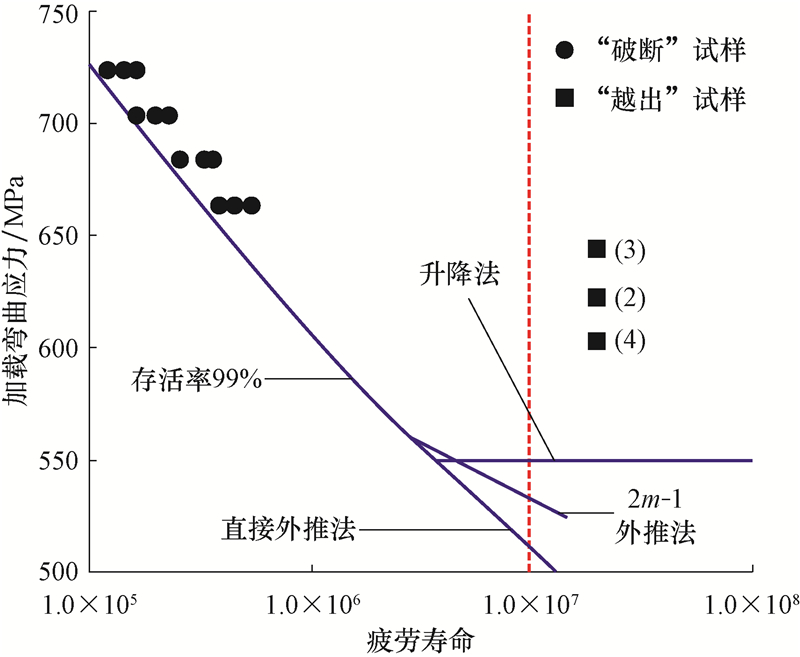
将升降法疲劳极限值、2m-1外推疲劳极限值与直接外推的疲劳极限值绘制成图(见图5和图6)。
|
| 图5 存活率为99%的S135钻杆外推曲线 Fig.5 Extrapolated curve of drill pipe S135 corresponding to 99% survival rate |
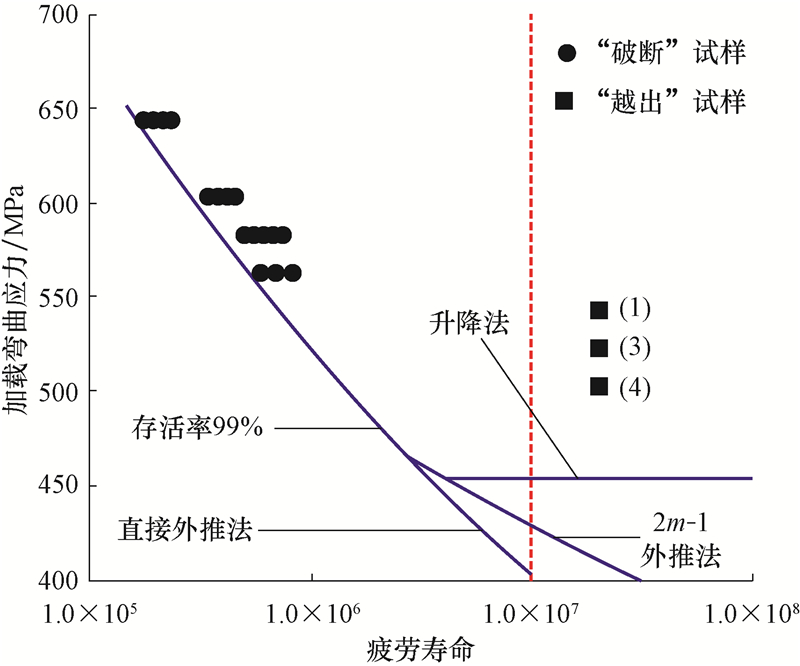
|
| 图6 存活率为99%的G105钻杆外推曲线 Fig.6 Extrapolated curve of drill pipe G105 corresponding to 99% survival rate |
从图5、图6可以看出:升降法试验得到的S135和G105钻杆的疲劳极限(存活率为99%,置信度为95%)为550.19和454.79 MPa;由直接外推法得到的疲劳寿命为1.0×107时的S135和G105钻杆对应疲劳极限分别为510.23和402.01 MPa;2m-1外推法得到的疲劳寿命为1.0×107时S135和G105钻杆的对应极限分别为532.95和428.98 MPa。2m-1外推法和直接外推法得到的疲劳极限均低于升降法试验所得出的疲劳极限,2m-1外推法预测的疲劳极限值更接近升降法试验值,直接外推法得出的疲劳极限远低于试验值,过于保守。
3 结 论1) 利用Basquin模型以及数理统计理论对中短寿命区成组法试验数据进行处理,可得到钻杆材料的S-N曲线,将其与升降法得出的疲劳极限绘制在同一S-lgN图中,可得到完整的概率-应力-疲劳寿命(P-S-N)曲线。
2) 由于升降法耗时、疲劳试样加工费用高,因此对疲劳极限的外推具有重要意义。对中短寿命区的曲线利用2m-1外推法和直接外推法进行外推,计算出钻杆材料的长寿命区疲劳寿命表达式及疲劳极限,并将其外推结果与升降法试验所得结果进行对比,证明2m-1外推法较直接外推法给出了合理的安全裕度,能较好地描述材料在长寿命区的应力-疲劳寿命关系。故在实际的工程应用中,建议在成组试验法基础上使用2m-1外推法进行外推。
| [1] |
刘志超,冯爽,姚久红,等.钻杆的失效分析和检测现状及其研究进展[J].热加工工艺,2015,44(6):8-11. Liu Zhichao,Feng Shuang,Yao Jiuhong,et al. Reaserch progress and detection current status and progress of drill pipe failure[J].Hot Working Technology,2015,44(6):8-11. |
| [2] |
刘永刚,陈绍安,李齐富,等.复杂深井钻具失效研究[J].石油矿场机械,2010,39(9):13-16. Liu Yonggang,Chen Shaoan, Li Qifu,et al. Study on failure drill string in complex deep well[J]. Oil Field Equipment,2010,39(9):13-16. |
| [3] |
万里平,孟英峰,杨龙,等.钻柱失效原因及预防措施[J]. 钻采工艺,2006,29(1):57-59. Wan Liping,Meng Yingfeng,Yang Long,et al. Failure cause and preventive measures of drill stem[J].Drilling & Production Technology,2006,29(1):57-59. |
| [4] |
王文龙,赵勤,李子丰,等.普光气田气体钻井钻具失效原因分析及预防措施[J].石油钻采工艺,2008,30(5):38-43. Wang Wenlong,Zhao Qin,Li Zifeng,et al. Cause analysis and precautions of drilling tools failure during gas drilling in Puguang Gas Field[J]. Oil Drilling & Production Technology,2008,30(5):38-43. |
| [5] |
林元华,罗宏志,邹波,等.钻柱失效机理及其疲劳寿命预测研究[J].石油钻采工艺,2004,26(1):19-22. Lin Yuanhua,Luo Hongzhi,Zou Bo,et al. Research on the failure mechanism and fatigue life predication of drill pipe[J].Oil Drilling & Production Technology,2004,26(1):19-22. |
| [6] |
吕拴录,倪渊诠,杨成新,等. 某油田钻具失效统计分析[J]. 理化检验,2012,48(6):414-418. Lv Shuanlu,Ni Yuanquan,Yang Chengxin,et al.Statistic analysis on drilling tools failure in one oil field[J]. Physical Testing and Chenmical Analysis,2012,48(6):414-418. |
| [7] | Lv Shuanlu,Feng Yaorong,Luo Faqian,et al. Failure analysis of IEU drill pipe wash out[J]. International Journal of Fatigue,2005,27(10/11/12):1360-1365. |
| [8] | Ziomek-Moroz M. Environmentally assisted cracking of drill pipes in deep drilling oil and natural gas wells[J]. Journal of Materials Engineering and Performance,2012,21(6):1061-1069. |
| [9] | Kohout J,Vechet S. A new function for fatigue curves characterization and its multiple merits[J]. International Journal of Fatigue,2001,23(2):175-183. |
| [10] | GB/T 4337—2008 金属材料 疲劳试验 旋转弯曲方法[S]. GB/T 4337—2008 Metallic materials-fatigue testing-rotating bar bending method[S]. |
| [11] | 陈传尧.疲劳与断裂[M]. 武汉:华中科技大学出版社,2001:47-54. Chen Chuanyao. Fatigue and fracture[M]. Wuhan: Huazhong University of Science & Technology Press,2001:47-54. |
| [12] |
王强,赵永翔,王欢.铁路D1车轮钢的疲劳可靠性寿命与强度的试验及表征[J].机械工程学报,2014,50(14):50-55. Wang Qiang,Zhao Yongxiang,Wang Huan. Experiments and characterization on the probabilistic fatigue lives and strengths of D1 railway wheel steel[J]. Journal of Mechanical Engineering,2014,50(14):50-55. |
| [13] |
杨冰,赵永翔,邬平波,等.16MnR钢焊接头的延拓概率疲劳S-N曲线[J].交通运输工程学报,2004,4(4):25-29. Yang Bing,Zhao Yongxiang,Wu Pingbo,et al. Extrapolation of probabilistic fatigue S-N curves on 16MnR steel weld joint[J]. Journal of Traffic and Transportation Engineering,2004,4(4):25-29. |


