利用ECS测井资料不但可以确定地层矿物含量,而且还可以确定地层的骨架参数和脆性指数,这对于准确评价页岩地层具有重要意义。但是利用ECS测井资料确定页岩地层矿物及含量时仍采用以前的统计模型,误差较大,需要建立新的模型进行解释。
ECS测井仪器由Schlumberger公司生产,是在GLT(geochemical logging tool)和RST(reservoir saturation tool)基础上发展起来的,主要由241Am-Be中子源和BGO晶体探测器组成,它通过中子源向地层中发射4 MeV的快中子,快中子与地层元素发生非弹性散射,之后快中子变为热中子,最后被周围的原子核俘获后释放伽马射线回到初始状态。BGO晶体探测器能记录256道俘获伽马能谱,经过解谱后得到H,Cl,Si,Ca,Fe,S,Ti和Gd等元素的含量,这个过程称为剥谱[1]。
ECS测井纵向分辨率可达到0.457 m,且ECS元素测井受钻井液和井眼环境影响较小,因此利用ECS测井资料能有效评价页岩地层的矿物类型和含量,并能进一步评价页岩地层的骨架密度和脆性指数,为页岩地层压裂改造提供依据。
1 现有ECS测井资料解释方法利用ECS测井资料能获得H,Cl,Si,Ca,Fe,S,Ti,Gd和Al等元素的相对含量,由于H和Cl元素主要存在地层流体中,与地层矿物相关性较小,在页岩地层矿物反演中难以使用;Ti和Gd在地层中属于微量元素,因此ECS测井能有效应用的元素为Si,Ca,Fe,S和Al。由于地层矿物与元素之间具有特定的关系(见表1),可以根据该关系利用ECS元素测井资料确定地层矿物的含量。
| 矿物 | Al | C | Ca | Fe | K | Mg | Mn | Na | S | Si |
| 石英 | 0.467 | |||||||||
| 钾长石 | 0.097 | 0.141 | 0.303 | |||||||
| 钠长石 | 0.103 | 0.088 | 0.321 | |||||||
| 正长石 | 0.194 | 0.144 | 0.202 | |||||||
| 白云母 | 0.191 | 0.013 | 0.078 | 0.001 | 0.001 | 0.005 | 0.212 | |||
| 黑云母 | 0.060 | 0.002 | 0.136 | 0.072 | 0.077 | 0.003 | 0.004 | 0.182 | ||
| 方解石 | 0.120 | 0.400 | ||||||||
| 白云石 | 0.130 | 0.217 | 0.132 | 0.210 | ||||||
| 高岭石 | 0.204 | 0.001 | 0.008 | 0.001 | 0.001 | 0.001 | 0.249 | |||
| 伊利石 | 0.132 | 0.005 | 0.048 | 0.045 | 0.012 | 0.004 | 0.205 | |||
| 蒙脱石 | 0.070 | 0.007 | 0.015 | 0.006 | 0.015 | 0.004 | 0.205 | |||
| 绿泥石 | 0.100 | 0.001 | 0.230 | 0.070 | 0.001 | 0.231 | ||||
| 海绿石 | 0.044 | 0.005 | 0.155 | 0.059 | 0.021 | 0.001 | ||||
| 铁白云石 | 0.116 | 0.194 | 0.162 | 0.035 | 0.027 | |||||
| 磷铁矿 | 0.104 | 0.482 | 0.535 | |||||||
| 黄铁矿 | 0.466 | |||||||||
| 赤铁矿 | 0.699 | 0.190 | ||||||||
| 石膏 | 0.233 | 0.240 | ||||||||
| 硬石膏 | 0.294 |
利用ECS测井资料反演地层矿物含量时,最早是利用氧闭合模型将元素含量转换成氧化物;后来有学者利用X荧光数据得到氧化物的含量与矿物含量之间的转换关系,也有人根据矿物试验建立了元素与矿物之间的转换关系[1, 2, 3],该转换关系是地层元素氧化物到矿物转化的基础;最近有学者用优化方法直接建立了页岩地层元素到矿物含量的计算公式[4] 。Schlumberger公司确定矿物质量分数是根据氧化物的质量或元素的质量,利用统计公式建立矿物含量之间的关系[5],运用Su元素含量来确定黄铁矿含量,通过SiO2,MgCO3,CaCO3和Fe含量确定泥质含量,用Ca和Mg元素确定灰岩和白云岩含量,剩下的部分就是石英、长石和云母的含量,具体的模型为:
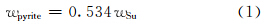
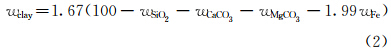
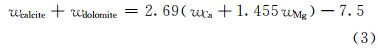
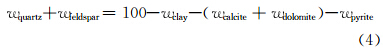
式中:wSu,wFe,wCa和wMg为元素测井中的硫、铁、钙和镁等元素的产额;wSiO2,wCaCO3和wMgCO3为利用Si,Ca和Mg等元素产额得到的元素氧化物、碳酸钙和碳酸镁的含量;wpyrite,wclay,wcalcite,wdolomite,wquartz和wfeldspar分别为黄铁矿、泥质、方解石、白云石、石英和长石的含量。
2 ECS测井资料解释新方法 2.1 页岩地层矿物模型和元素测井响应方程页岩地层广泛存在于海相、陆相及海陆过渡相。陆相地层通常仅包含泥岩、砂岩和长石等碎屑岩矿物,海相地层包含泥岩、方解石和白云岩3种矿物,但海陆过渡相地层不仅有黏土矿物和碳酸盐矿物存在,还包含硅质类矿物,甚至其他矿物。总之,页岩地层矿物组成类型繁多,不仅包含硅质、钙质矿物和黏土矿物,还包含有机质和黄铁矿,甚至还有云母、硬石膏和有机质。
有机质的主要元素是C,由于ECS测井仪器无法测量C元素的含量,所以不能用ECS测井资料评价页岩地层中有机碳的含量,只能用于确定页岩地层中其他矿物的含量。
由于地层中每种类型矿物中的元素含量通常固定不变(见表1),因此结合地层中矿物的含量就能得出ECS元素测井的响应方程。ECS元素测井在一定深度时不同矿物的响应方程为:
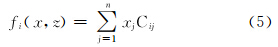
式中:fi(x,z)为第i种元素在对应地层深度z和不同矿物下的总含量;Cij为第i种元素在第j种矿物中的质量分数;xj为第j种矿物的含量。
2.2 解释方法ECS测井资料解释方法根据广义反演理论,利用地层矿物与元素含量之间的关系(见表1),通过构造地层不同矿物模型下的元素含量响应方程,反演计算构造响应方程的理论测井值,并与实际测井值比较,两者充分逼近且不大于设定误差时,计算出的理论测井值就反映实际地层中矿物的含量。由非线性加权最小二乘原理与误差理论建立元素测井最优化解释目标函数数学模型:
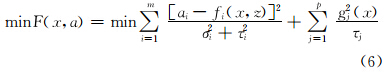
式中:ai为第i种元素的含量,%;x为反演矿物含量,%;z为测井深度,m;σi为第i种元素的不确定性系数,由解谱误差决定;τi为构造的第i种元素测井响应方程的误差;F(x,a)为最优化元素测井解释的目标函数;gj(x)与τj为x的第j种不等式约束及其误差。
构造元素测井响应方程和响应方程误差后结合元素的不确定性和约束条件,应用最优化反演算法就可以进行反演求解,反演计算时将多维搜索算法中的变尺度法和一维搜索算法中的抛物线插值法相结合[6, 7]。采用一维搜索算法计算反演变量变化过程中的最佳步长,求出该抛物线的极小点。利用BFGS变尺度法能快速确定多个反演变量的搜索方向。
2.3 页岩地层约束条件的施加最优化反演目标模型(式(6))是一种较通用的模型,反演的准确度依赖于元素测井响应方程和所施加的约束条件。从元素测井响应方程式(5)可看出,ECS元素测井能识别5种主要元素(Si,Ca,Fe,S和Mg),而页岩地层矿物模型有10种以上矿物,通常情况下页岩也有5种以上矿物,因此该目标函数的反演即求解欠定方程组。从理论上讲,欠定方程组具有多个解,为了得到合理的解释结果,必须施加矿物类型、矿物含量等约束条件。
矿物类型约束是主要约束条件之一,根据页岩地层的实际矿物类型确定反演目标函数的主要矿物类型。针对礁石坝页岩地层实际情况选择黄铁矿、方解石、石英、长石、绿泥石、伊利石等6种矿物进行反演。
页岩地层中每种矿物含量xi在求解过程中有一定的约束。xi的约束条件为:

ECS原始测井资料,经过解谱后得到地层每种元素的相对含量。通过反演后得到地层内每种矿物的相对含量,其满足地层矿物含量之和等于1,即地层总矿物的约束条件为:

对于反演页岩地层中6种矿物的情况,利用式(7)和式(8)能有效反演出地层中矿物的含量。对于超过6种矿物的情况,例如增加白云石和一种黏土矿物,需要根据矿物含量进一步约束,具体来说,确定该矿物在页岩地层中的最大含量和最小含量,施加其约束条件为xmax≥xi≥xmin。
2.4 反演结果的评价反演结果通常采用拟合系数法、置信区间法、目标函数最优值和减小非相关函数法评价。笔者采用置信区间法和目标函数最优法来判别。置信区间由曲线测量误差来控制,若构建曲线在置信区间内说明反演结果可靠。目标函数最优法是衡量理论测井曲线逼近实际测井曲线的匹配程度,目标函数F(x,a)可作为优化计算结果的相对质量指示,F(x,a)越小,则反演结果越好。
3 现场应用笔者利用建立的页岩地层ECS测井解释方法,对我国某气田A区块X井的页岩地层ECS测井资料进行了处理解释。
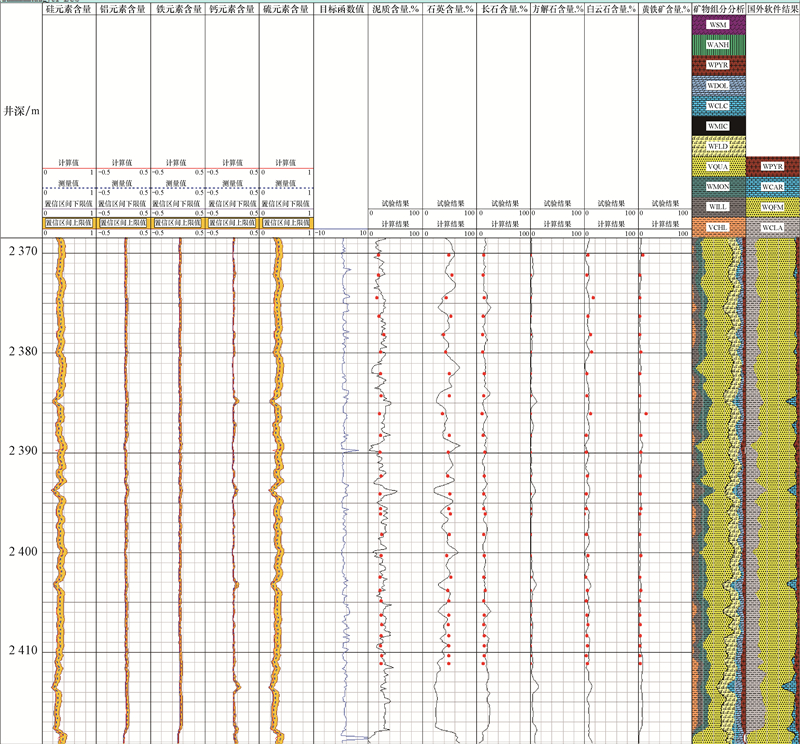
3.1 确定地层矿物含量A区块优质页岩主要分布在下古生界志留系下统龙马溪组,岩性主要以黄灰色页岩、粉砂质页岩夹薄层透镜状灰岩为主。根据该区块的实际情况,选择Si,Al,Fe,Ca,S和K元素反演出10种矿物的含量,10种矿物分别是石英、长石、灰岩、白云岩、伊利石、绿泥石、蒙脱石、黄铁矿、云母和硬石膏,反演时根据实际情况选择矿物类型。图1为A区块X井的ECS测井资料解释结果,图中第2道至第6道为ECS元素相对含量、重构元素响应值和反演结果的置信区间,第7道为目标函数值,第8道至第13道为反演的矿物含量,第14道为反演出的:伊利石(浅灰色)、绿泥石(灰色)、蒙脱石(深绿色)、石英(黄色)、长石(淡黄色)、方解石(蓝色)、白云岩(浅蓝色)和黄铁矿(暗红色)等矿物,第15道为国外软件根据式(1)—式(4)的处理结果。从图1可看出,反演结果与岩心矿物分析结果(红色离散点)有较好的一致性。
|
| 图1 A区块X井2 367.00~2 417.00 m井段ECS元素测井反演矿物的含量 Fig.1 Minerals and their contents obtained by inversion calculation of ECS logging data in the section from 2 367.00 m to 2 417.00 m in well X of Block A |
地层中通常包含矿物骨架和流体,确定页岩地层矿物骨架密度有利于进一步评价地层流体含量和孔隙度。页岩地层除骨架矿物和流体之外,还包含有机质,准确确定页岩地层矿物类型和含量及骨架密度是评价页岩地层的基础和重要环节。由于每种矿物对应固定的骨架密度,于是根据地层中的矿物类型和含量就可以计算出地层的骨架密度,计算模型为:
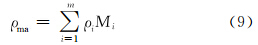
式中:ρma为页岩地层骨架密度;m为地层中矿物种类;Mi为地层中第i种矿物的质量分数;ρi为第i种矿物对应的骨架密度。
图2为X井页岩地层在利用ECS测井资料计算地层矿物含量的基础上进一步计算出的地层骨架密度。从图2可看出,该地层骨架密度为2.65~2.75 g/cm3,与地层实际情况相符。
|
| 图2 X井页岩地层ECS资料解释及骨架密度 Fig.2 The gain density of the shale formation of well X in Block A interpreted with ECS logging data |
脆性指数是页岩地层压裂的重要参数,通常根据脆性指数进行压裂选层。脆性指数通常通过岩心矿物分析试验和岩石力学试验评价,用脆性矿物含量表征地层的脆性。
Jarvie用脆性矿物含量占总矿物的比来表示脆性指数,其中脆性矿物包含石英和碳酸盐岩[8]。其表达式为:
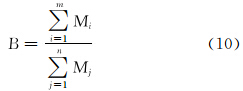
式中:B为页岩地层的脆性指数;m为脆性矿物种类;n为总矿物种类;Mi为第i种脆性矿物含量;Mj为第j种矿物的含量,通常情况下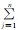 Mj=1。
Mj=1。
Dan Buller在式(10)的基础上,给每种矿物增加了一个权重系数[9],但并没有给出权重系数的求取方法。Dan Buller脆性指数的表达式为:
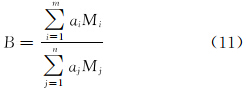
式中:aj为第j种矿物的权重系数;ai为第i种脆性矿物的权重系数。
笔者通过引入每种矿物的断裂韧度,并将其作为矿物的权重系数,建立了页岩地层脆性指数评价模型[10],该模型不受流体性质和有机质的影响。其表达式为:
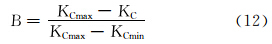
式中:KC为页岩地层中矿物的断裂韧度,MPa·m1/2;KCmax和KCmin分别为页岩地层的最大和最小断裂韧度,MPa·m1/2。
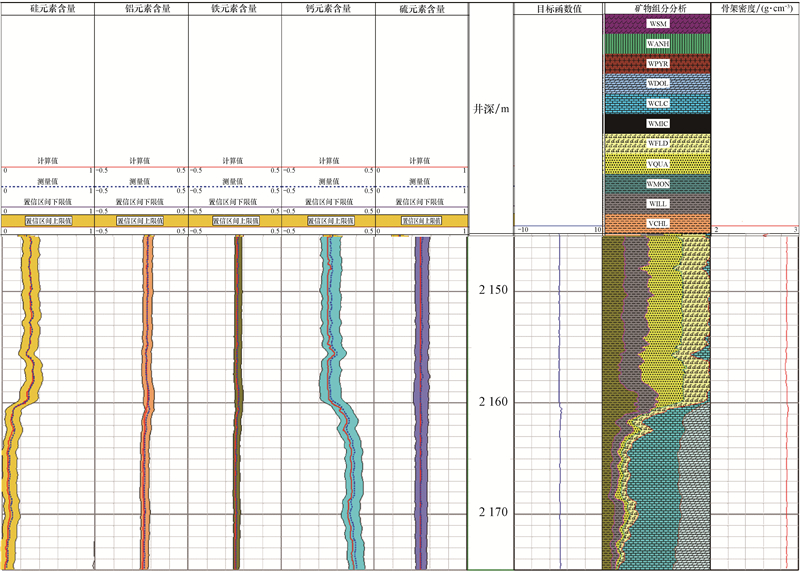
图3为利用X井页岩地层ECS测井资料计算地层矿物含量的基础上进一步计算出的地层脆性指数,图中第7道为利用ECS测井资料计算的页岩地层矿物含量,第8道中红色曲线是用式(12)计算的脆性指数,蓝色曲线是用式(10)计算的脆性指数。从图3可看出,用式(10)计算的脆性指数比用式(12)计算的略低,即用断裂韧度和矿物含量计算的脆性指数比仅用矿物含量计算的脆性指数略高,当碳酸盐含量高时,用式(12)计算的更高。
|
| 图3 X井页岩地层ECS资料解释及脆性指数 Fig.3 The brittleness index of the shale formation of Well X in Block A interpreted with ECS logging data |
1) 利用优化反演算法建立了页岩地层ECS测井解释方法,能同时反演出6~8种矿物及含量。
2) 实例证明,利用ECS测井资料优化反演地层矿物类型和含量是可靠的,评价结果与岩心试验结果具有较好的一致性。
3) 在反演计算地层矿物含量的基础上,能进一步计算地层的骨架密度和脆性指数,有利于准确评价页岩地层的孔隙度、流体和脆性,以指导压裂设计与施工。
| [1] | Hertzog R,Colson L,Seeman O,et al.Geochemical logging with spectrometry tools[R].SPE 16792,1989. |
| [2] | Harvey P K,Lofts J C,Lovell M A.Mineralogy logs:element to mineral transforms and compositional colinearity in sediments:SPWLA the 33rd Annual Logging Symposium,Houston,June 14-17,1992[C]. |
| [3] | Herron S L,Herron M M.Quantitative lithology:An application for open and cased hole spectroscopy:SPWLA the 37rd Annual Logging Symposium,New Orleans,June16-19,1996[C]. |
| [4] | Quirein J,Witkowsky J,Truax J A,et al.Integrating core data and wireline geochemical data for formation evalution and characterization of shale gas reservoirs[R].SPE 134559,2010. |
| [5] | Herron M M,Herron S L,Grau,J A,et al.Real-time petrophysical analysis in siliciclastics form the integration of spectroscopy and triple-combo logging[R].SPE77631,2002. |
| [6] |
雍世和,孙建孟.最优化测井解释[M].东营:石油大学出版社,1995:87-119. Yong Shihe,Sun Jianmeng.Optimization logging interpretation[M].Dongying:Petroleum University Press,1995:87-119. |
| [7] |
肖立志.一种改进的数字测井最优化解释方法[J].石油学报,1991,12(2):40-50. Xiao Lizhi.An improved interpretation method for digital log,Acta Petrolei Sinica[J].Acta Petrolei Sinica,1991,12(2):40-50. |
| [8] | Jarvie D M,Hill R J,Ruble T E,et al.Unconventional shale-gas systems:the Mississippian Barnett Shale of north-central Texas as one model for thermogenic shale-gas assessment[J].AAPG Bulletin,2007,91(4):475-499. |
| [9] | Buller D,Hughes S N,Market J,et al.Preophysical evaluation for enhancing hydraulic stimulation in horizontal shale gas wells[R].SPE 132990,2010. |
| [10] |
廖东良,肖立志,张元春.基于矿物组分与断裂韧度的页岩地层脆性指数评价模型[J].石油钻探技术,2014,42(4):37-41. Liao Dongliang,Xiao Lizhi,Zhang Yuanchun.Evaluation model for shale brittleness index based on mineral content and fracture toughness[J].Petroleum Drilling Techniques,2014,42(4):37-41. |


