2. 中国石油大学(华东)海洋油气装备与安全技术研究中心, 山东青岛 266580
2. Research Center for Offshore Engineering and Safety Technology, China University of Petroleum (Huadong), Qingdao, Shandong, 266580, China
南海台风活动频繁,在台风作用下采用锚泊定位的浮式钻井装置将会产生大的漂移,对锚泊系统和水下管柱造成严重威胁,甚至引发钻井事故[1]。因此,研究台风作用下锚泊定位半潜式平台的动力特性,对于指导平台科学合理抗台风具有十分重要的意义。目前,国内外对于锚泊系统进行了较多的理论研究:袁杨等[2]对锚泊系统失效后的半潜式平台的动力特性进行了相关研究;袁梦等[3]从势能理论角度入手,结合悬链线方程,建立了锚泊系统的数学模型;Ruoyu Zhang等[4]针对浮式风力发电机,采用频域与时域的计算方法,得到了该浮式结构的动力响应特性;V.F.Matos等[5]采用理论推导和试验方法,对深吃水半潜式平台进行了各自由度的二阶运动分析;K.A.Belibassakis[6]采用边界元方法对浮式结构进行了水动力数值分析,得到了其运动特性;Haixiao Liu等[7]对人工合成纤维缆绳进行了动力分析,研究了其在循环载荷作用下的非线性动态特性。上述研究对于建立简单锚泊系统分析理论模型、揭示锚泊系统的响应规律有着重要作用,但均没有详细分析台风作用下锚泊定位半潜式平台的动力特性,相关模型既无法定量评估复合式锚泊系统的安全性,也无法针对现场问题进行快速响应并提出解决方案。为此,笔者在前人的研究基础上,采用水动力学计算软件ANSYS-AQWA建立了平台-锚泊系统耦合水动力学分析模型,对锚泊定位的半潜式钻井平台进行了详细的动力学分析,得到了锚链完整和局部断裂情况下平台漂移量和锚泊系统的安全系数,并对极端情况下锚链断裂后剩余锚链的锚泊定位能力和其他锚链的安全性进行了评价,以对我国南海锚泊定位钻井和生产装置的锚泊系统设计、分析和安全评价提供一定参考。
1 平台动力特性理论基础及分析模型 1.1 理论基础采用三维势流理论可以计算得到平台的附加质量矩阵和阻尼矩阵,以及平台运动的幅值响应算子。将频域计算结果转化成时域结果,结合运动方程进行时域计算,可得到平台在外界荷载作用下的时域动态结果[2]。平台运动方程为[2, 8]:
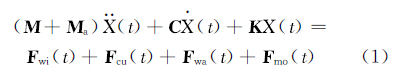
式中:M为平台质量矩阵;Ma为附加质量矩阵;C为阻尼矩阵;K为平台系泊刚度矩阵;Fwi为风力矩阵;Fcu为海流力矩阵;Fwa为波浪力矩阵;Fmo为系泊力矩阵;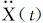 为平台运动的加速度,m/s2;
为平台运动的加速度,m/s2;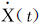 为平台运动的速度,m/s;X(t)为平台运动的位移,m;t为时间,s。
为平台运动的速度,m/s;X(t)为平台运动的位移,m;t为时间,s。
将势流理论与莫里森方程相结合,得到平台所受波浪力荷载。可根据风力系数与流力系数得出风力和流力荷载[9],计算式为:
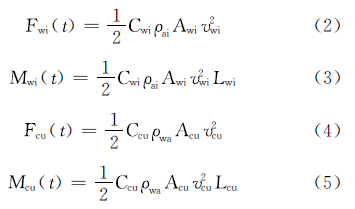
式中:Cwi和Ccu分别为风力系数和流力系数;ρai和ρwa为空气和海水的密度,kg/m3;Awi和Acu为平台的迎风面积和迎流面积,m2;vwi和vcu为风速和流速,m/s;Fwi和Fcu分别为风力和海流力,N;Mwi和Mcu分别为风倾力矩和流倾力矩,N·m;Lwi和Lcu为风倾力臂和流倾力臂,m。
1.2 基于ANSYSAQWA的平台-锚泊系统耦合模型以南海某深水半潜式钻井平台为研究对象。该平台基本尺寸为82.30 m×60.96 m×41.66 m,作业吃水深度20 m,平台质量2.8×104 t。该平台采用锚泊定位,锚链有8根。根据上述参数和平台的结构,采用ANSYS-AQWA建立该平台的湿表面模型,如图1所示(图中,红色部分为绕射辐射单元,采用三维势流理论进行水动力分析;黄色部分为莫里森单元,采用莫里森方程进行水动力分析[10, 11])。建模时,平台由shell和pipe单元构成,共计8 979个shell单元和53个pipe单元。

|
| 图1 基于ANSYS-AQWA的半潜式平台湿表面模型 Fig.1 The wetted surface model of semi-submersible platform base on ANSYS-AQWA |
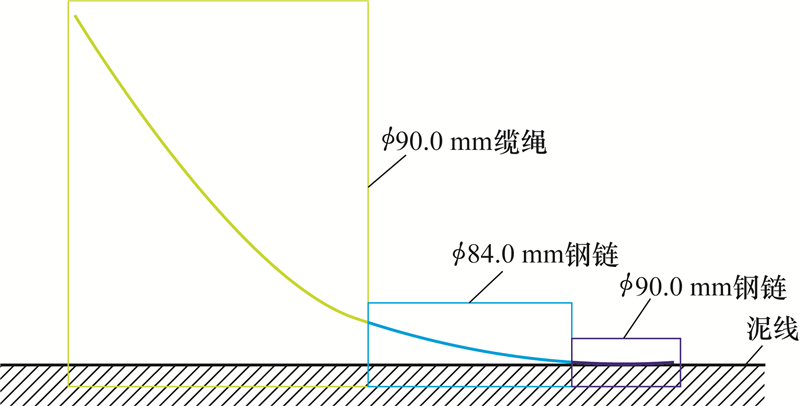
半潜式钻井平台采用复合式锚链定位,其下端分别为长70 m的φ90.0 mm钢链及长550 m的φ84.0 mm钢链,最上端为φ90.0 mm的缆绳。钢链和缆绳的材料属性见表1,各锚链所选缆绳类型及布锚基本参数见表2。
| 材料 | 干重/(kg·m-1) | 轴向刚度/MN | 破坏强度/MN | |
| φ90.0 mm钢链 | 154 | 702.13 | 7.54 | |
| φ84.0 mm钢链 | 141 | 611.64 | 9.37 | |
| φ90.0 mm缆绳1 | 29 | 561.11 | 6.17 | |
| φ90.0 mm缆绳2 | 29 | 374.06 | 5.20 |
| 锚链号 | 布锚角度/(°) | 预张力/kN | 缆绳抛出长度/m | 缆绳类型 |
| 1 | 22.5 | 863.38 | 1 577.0 | φ90.0 mm缆绳1 |
| 2 | 67.5 | 826.14 | 1 651.4 | φ90.0 mm缆绳2 |
| 3 | 112.5 | 834.96 | 1 611.5 | φ90.0 mm缆绳1 |
| 4 | 157.5 | 865.34 | 1 591.2 | φ90.0 mm缆绳1 |
| 5 | 202.5 | 853.58 | 1 569.6 | φ90.0 mm缆绳1 |
| 6 | 247.5 | 861.42 | 1 258.9 | φ90.0 mm缆绳1 |
| 7 | 292.5 | 824.18 | 1 565.6 | φ90.0 mm缆绳1 |
| 8 | 337.5 | 865.34 | 1 578.8 | φ90.0 mm缆绳1 |
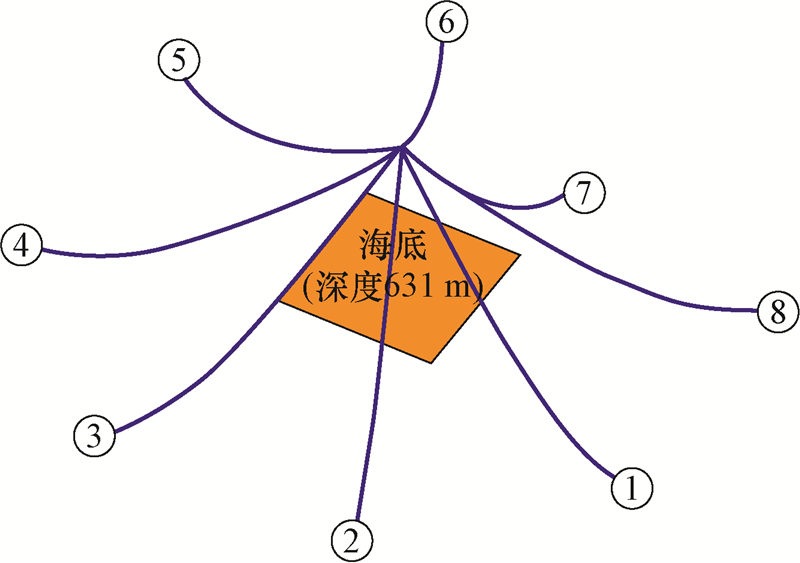
根据平台基本模型与锚泊系统参数,建立了深水平台-锚泊系统耦合动力分析模型,如图2所示(图中数字代表各条锚链的编号)。锚链组合形式如图3所示,为非对称式布锚方式。采用ANSYS-AQWA对其进行动力学分析,即获得平台的动力特性。
|
| 图2 耦合动力分析模型 Fig.2 Coupled dynamic analysis model |
|
| 图3 锚链组合形式示意 Fig.3 The schematic diagram for distribution of anchoring chain elements |
考虑重现期为1年的台风荷载,根据现场井位环境参数,近海面海流流速为1.12 m/s,平均风速为42.52 m/s。随机波面采用P-M波浪谱,显著波高为9.24 m,跨零周期为12.6 s。
2 平台锚泊系统动力分析与讨论根据上述耦合分析模型及确定的台风参数,对台风作用下平台与锚泊系统的动力特性进行计算分析,确定平台在台风作用下的漂移量与锚链的安全系数。通过与API规范相关规定进行对比,校核平台锚泊系统的安全性[12]。
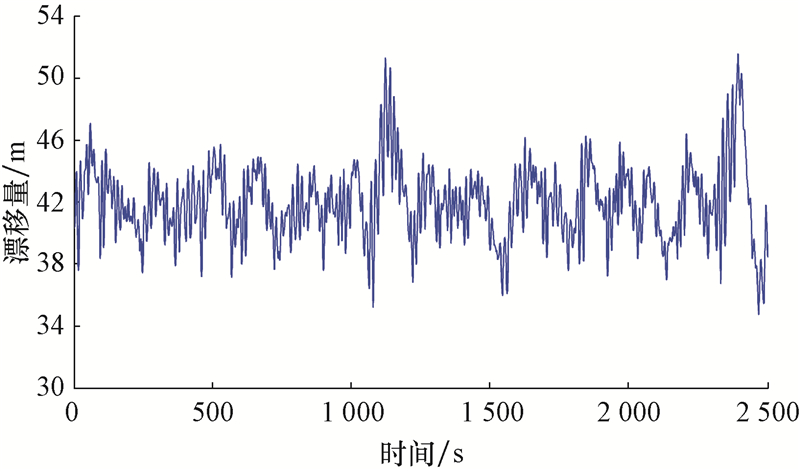
2.1 平台漂移量分析在进行平台漂移动力分析时,既要关注平均漂移量,又要关注最大漂移量。前者主要用于判断平台漂移量是否满足正常钻井作业需求,后者主要用于判断是否需要解脱隔水管与井口的连接。台风条件下,环境荷载入射角为90°时的平台漂移时程曲线如图4所示。
|
| 图4 环境荷载入射角90°时的平台漂移量 Fig.4 The drift distance of platforms when the incidence angle of the environmental load is 90° |
由图4可知,台风作用下平台在顺风向产生较大漂移量,然后在新的相对平衡位置处呈不规则振荡运动。
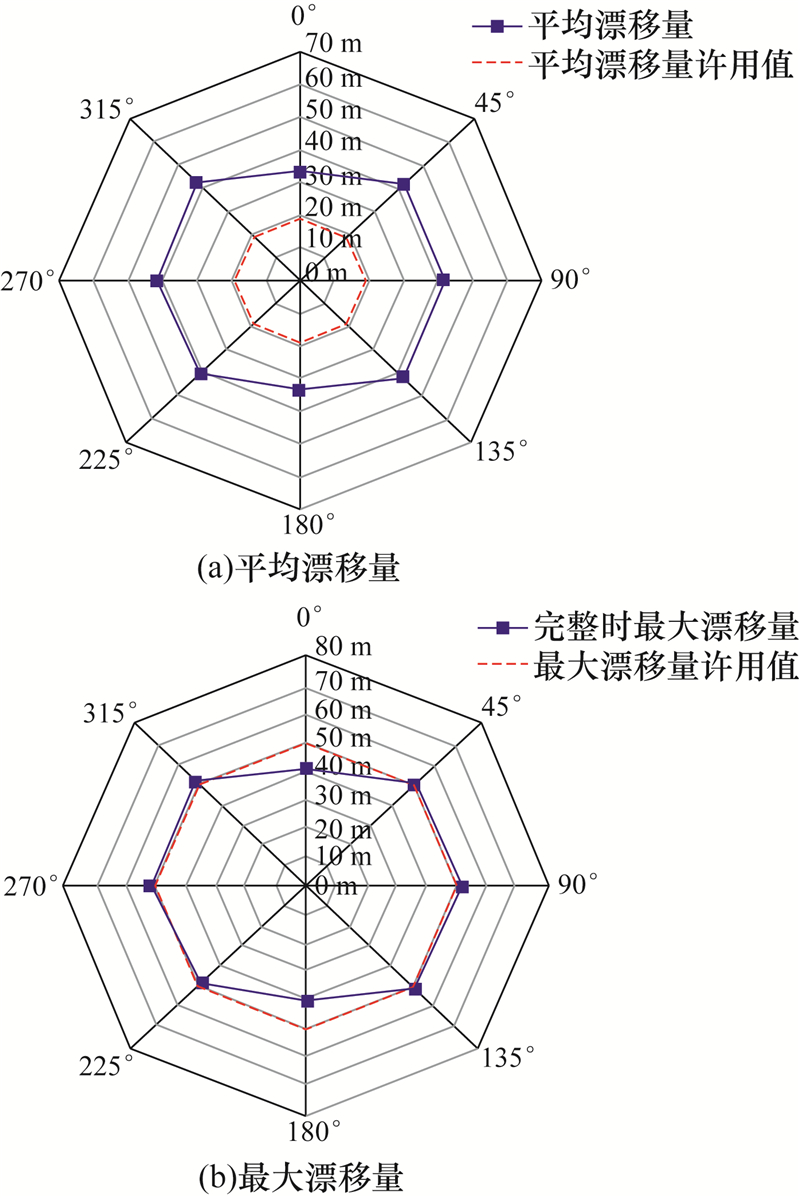
环境荷载入射角为0°,45°,90°,135°,180°,225°,270°和315°时平台的平均漂移量和最大漂移量分析结果见图5。图5(a)中,红线代表可进行正常钻井的平台平均漂移许用值,蓝线代表平台平均漂移量计算值;图5(b)中,红线代表需启动解脱的平台最大漂移许用值,蓝线代表平台最大漂移量的计算值。
|
| 图5 锚泊系统完整时的平均漂移量和最大漂移量 Fig.5 The average and maximum drift distances of the platform with an intact mooring system |
由图5可知,平台在台风作用下的平均漂移量和最大漂移量的计算值均大于相应的许用值。根据API规范,当平均漂移量的计算值大于其许用值时应停止钻井作业,此时水下管柱与井口可保持连接;但当最大漂移量的计算值大于其许用值时,应解脱隔水管与井口的连接,以避免因平台漂移较大造成隔水管柱或者张紧系统损坏[13]。
2.2 锚泊系统强度分析同样,环境荷载以45°为间隔对锚链动张力进行分析,获得不同环境荷载入射方向上主要受力锚链的最小安全系数。环境荷载入射角为90°时2号锚链的动张力时程曲线如图6所示。
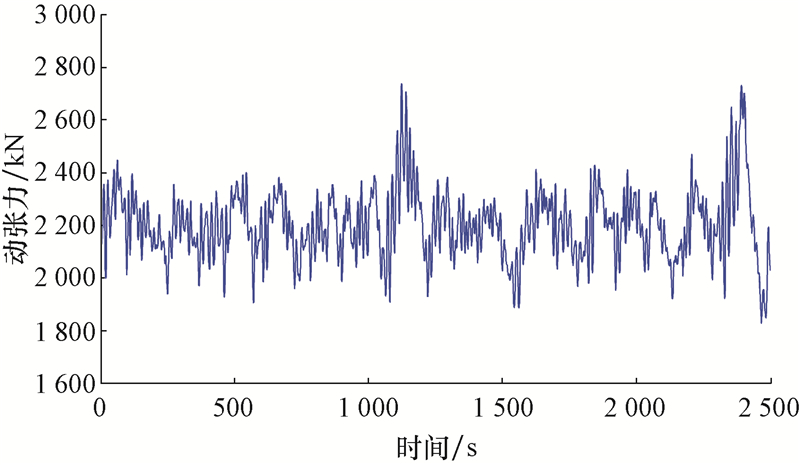
|
| 图6 环境荷载入射角为90°时2号锚链的动张力曲线 Fig.6 The dynamic tension curve of NO.2 anchor chain when the incidence angle of the environmental load is 90° |
由图6可知,在台风作用下2号锚链的瞬时最大动张力达到2 739 kN。考虑到锚链的断裂强度为5 200 kN,此时该条锚链的最小安全系数为1.9。同理,可获得其他环境入射方向上主要受力锚链的瞬时最大动张力和最小安全系数,统计结果见表3。
API规范对锚泊系统最小安全系数的规定为,当锚泊系统完整时各锚链安全系数应大于1.67[12]。由表3可知,各环境入射方向上,主要受力锚链的最小安全系数均在API规定的许用值范围内,说明锚泊系统在该台风条件下具有足够的剩余强度,可维持锚泊系统的完整性。但对比可知,2号锚链的安全系数最小,主要原因是其破坏强度较其他锚链较低,造成其强度余量较小,可能成为整个锚泊系统的最薄弱环节,需结合当地风向及海流流向判断2号锚链是否会成为主要受力锚链,并加以优化。
| 环境入射角/(°) | 最大张力/kN | 安全系数 | 安全系数许用值 |
| 注:“()”内数字为主要受力锚链编号。 | |||
| 0 | 2 537(4) | 2.43 | 1.67 |
| 45 | 3 061(4) | 2.02 | 1.67 |
| 90 | 2 739(2) | 1.90 | 1.67 |
| 135 | 2 743(2) | 1.90 | 1.67 |
| 180 | 2 462(8) | 2.51 | 1.67 |
| 225 | 3 017(8) | 2.05 | 1.67 |
| 270 | 2 861(7) | 2.16 | 1.67 |
| 315 | 3 142(5) | 1.96 | 1.67 |
在极端条件下,锚泊系统中某一条锚链有可能由于强度不足而发生断裂,并由此引发后续的连锁反应,如平台的漂移量持续增大、其他锚链相继发生断裂等。于是,对锚链损坏后平台-锚泊系统的动力特性进行分析,对于掌握锚链断裂后平台运动和剩余锚链张力重新分配规律、研究不完整锚泊系统的剩余强度具有较大意义。
3.1 平台漂移量根据表3中锚链完整情况下各条锚链的最小安全系数计算结果,进行一条锚链断裂条件下的平台-剩余锚泊系统动力分析,确定平台漂移量的变化规律。分析前提是剩余锚泊系统仍然具有与原有完整锚泊系统相同的定位能力。
台风条件下,环境入射角为90°时平台漂移时程曲线如图7所示。
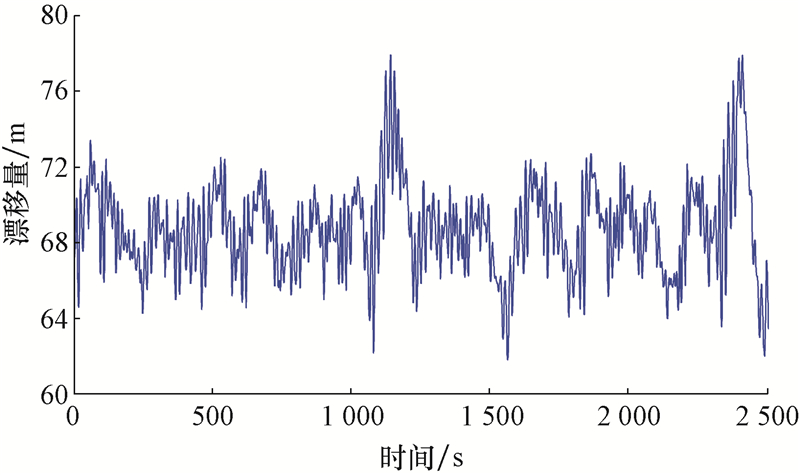
|
| 图7 环境入射角为90°时的平台漂移量 Fig.7 The drift distance of the platform when the incidence angle of the environmental load is 90° |
由图7可知,损坏一条锚链后,相对于锚链完整状态,整个钻井平台的漂移量明显增大,瞬时最大值接近80 m。
同样,以45°为间隔,计算0°,45°,90°,135°,180°,225°,270°和315°等环境入射角下平台的平均漂移量和最大漂移量并进行统计,结果见图8。
由图8可知,2号锚链断裂后,平台的平均漂移量为60~70 m,最大漂移量为70~80 m,表明一条锚链断裂后,剩余锚链的回复力明显减小,对平台的定位能力下降,导致平台的漂移量增大1.5倍左右。
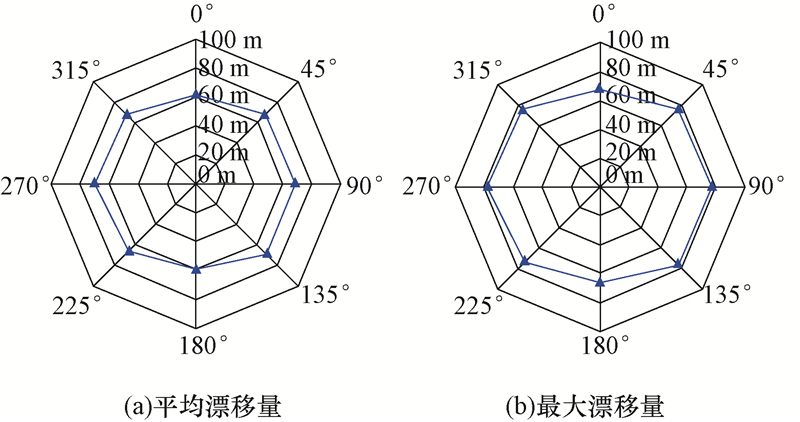
|
| 图8 锚链损坏后平台的平均漂移量和最大漂移量 Fig.8 The mean and max drift distances of the platform with a damaged mooring system |
当损坏一条锚链后,整个锚泊系统的张力将在剩余的各条锚链上重新分布。如果2号锚链发生断裂,环境入射角为90°时,分析得到相邻的3号锚链的动张力时程曲线,如图9所示。
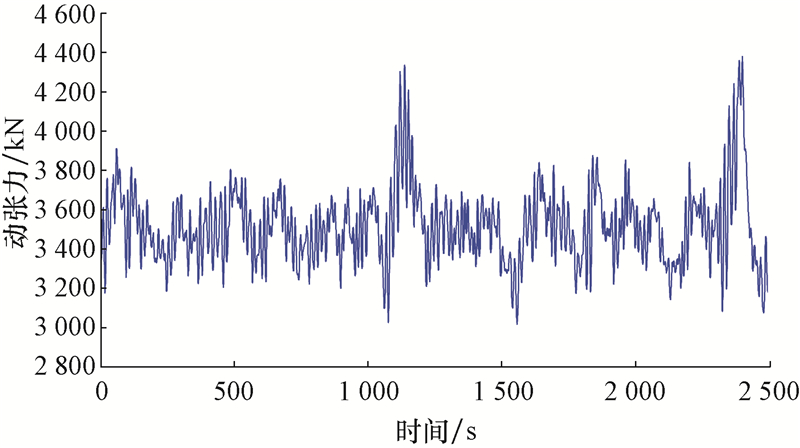
|
| 图9 环境入射角为90°时3号锚链的动张力 Fig.9 The dynamic tension of NO.3 anchor at the environmental incidence angle of 90° |
由图9知,3号锚链的动张力为3 000~4 400 kN,较锚链完整时的动张力约增大2 000 kN,表明损坏一条锚链后,剩余锚泊系统的动张力显著增大。
不同环境入射角条件下剩余锚链系统的最小安全系数计算结果见表4。
表4中,以环境入射角0°为例,该工况下通过分析锚链完整条件下的锚泊系统动张力,得知4号锚链的最小安全系数最小,于是假定该条锚链首先断裂。然后进行剩余锚泊系统的张力重分布研究和动张力分析,确定5号锚链的最小安全系数最小,为1.52,仍高于规范要求的最小值1.25[12],表明此时剩余锚泊系统虽然定位能力较差,但是锚泊系统是安全的,不会发生其他锚链相继断裂的连锁反应。
| 环境入射角/(°) | 损坏锚链 | 最大动张力/kN | 最小安全系数 | 安全系数许用值 |
| 注:“()”内的数字代表安全系数最小的锚链号。 | ||||
| 0 | 4 | 4 058(5) | 1.52 | 1.25 |
| 45 | 4 | 4 353(3) | 1.42 | 1.25 |
| 90 | 2 | 4 377(3) | 1.41 | 1.25 |
| 135 | 2 | 4 883(1) | 1.26 | 1.25 |
| 180 | 8 | 3 994(1) | 1.54 | 1.25 |
| 225 | 8 | 4 243(7) | 1.45 | 1.25 |
| 270 | 7 | 4 512(6) | 1.37 | 1.25 |
| 315 | 5 | 4 480(6) | 1.38 | 1.25 |
当然,也有比较危险的工况,譬如当环境入射角为135°时,台风条件下完整锚泊系统分析表明2号锚链首先发生断裂。对剩余锚泊系统重新进行计算和分析,结果表明1号锚链的最小安全系数为1.26,接近API规定的安全系数许用值,安全储备较差。但对于整个锚泊系统的安全评估,需要结合表4中的所有分析结果才能得到比较有价值的结论。
4 结 论1) 利用ANSYS-AQWA水动力计算软件将绕射辐射单元与莫里森单元相结合,建立了半潜式平台-锚泊系统耦合动力计算模型。采用三维势流理论和莫里森方程,可以较好地模拟锚泊定位半潜式平台与锚泊系统的动力学特性。
2) 台风作用下需要计算锚泊定位半潜式平台各个环境入射方向上的漂移量及锚链动张力。通过对比平台漂移量与API规定的漂移量许用值,确定隔水管柱的作业模式。通过计算不同环境入射方向上各锚链的动张力,确定主要受力锚链的最小安全系数,并与API安全系数许用值对比,评估锚泊系统的安全性。
3) 研究损坏一条锚链后平台-锚泊系统的耦合动力特性,发现平台的漂移量将明显增大,约为锚链完整时漂移量的1.5倍。断裂后主要受力锚链为断裂锚链的相邻锚链,其最大动张力明显增大,最小安全系数已经接近API规定的极限值。这表明当一条锚链断裂后,极有可能造成剩余锚泊系统连续性破坏,并有可能导致更严重的后果。
| [1] |
陈维杰,陈国明,朱本瑞,等.强台风下导管架平台风载荷数值仿真分析[J].中国海上油气,2013,25(3):73-77. Chen Weijie,Chen Guoming,Zhu Benrui,et al.Numerical simulation of wind load on jacket platform under strong typhoon[J].China Offshore Oil and Gas,2013,25(3):73-77. |
| [2] |
袁杨,汪学锋,张嫦利.半潜式平台系泊系统失效模式下动力响应分析[J].中国海洋平台,2015,30(2):36-41,47. Yuan Yang,Wang Xuefeng,Zhang Changli.Dynamic analysis on the impact of failure models for a mooring positioning system of a semi-submersible platform[J].China Offshore Platform,2015,30(2):36-41,47. |
| [3] |
袁梦,范菊,朱仁传,等.基于悬链线理论的系泊系统势能[J].上海交通大学学报,2011,45(4):597-603. Yuan Meng,Fan Ju,Zhu Renchuan,et al.Potential energy study of mooring system based on catenary method[J].Journal of Shanghai Jiaotong University,2011,45(4):597-603. |
| [4] | Zhang Ruoyu,Tang Yougang,Hu Jun,et al.Dynamic response in frequency and time domains of a floating foundation for offshore wind turbines[J].Ocean Engineering,2013,60(1):115-123. |
| [5] | Matos V F,Simos A N,Sphaier S H.Second-order resonant heave,roll and pitch motions of a deep-draft semi-submersible:theoretical and experimental results[J].Ocean Engineering,2011,38(17):2227-2243. |
| [6] | Belibassakis K A.A boundary element method for the hydrodynamic analysis of floating bodies in variable bathymetry regions[J].Engineering Analysis with Boundary Elements,2008,32(10):796-810. |
| [7] | Liu Haixiao,Huang Wei,Lian Yushun,et al.An experimental investigation on nonlinear behaviors of synthetic fiber ropes for deepwater moorings under cyclic loading[J].Applied Ocean Research,2014,45(1):22-32. |
| [8] |
张浩,陈国明,郑纯亮,等.内波参数对半潜式钻井平台漂移量的影响[J].石油钻采工艺,2015,37(1):39-42. Zhang Hao,Chen Guoming,Zheng Chunliang,et al.Effect of internal wave parametres on drifting quantity of semi-submersible drilling platform[J].Oil Drilling & Production Technology,2015,37(1):39-42. |
| [9] |
张威.深海半潜式钻井平台水动力性能分析[D].上海:上海交通大学船舶海洋与建筑工程学院,2007. Zhang Wei.Hydrodynamic analysis for a deep-water semi-submersible drilling platform [D].Shanghai:Shanghai Jiaotong University,School of Naval Architecture,Ocean Engineering,2007. |
| [10] |
闫功伟,欧进萍.基于AQWA的张力腿平台动力响应分析[J].东南大学学报:自然科学版,2009,39(增刊2):304-310. Yan Gongwei,Ou Jinping.Dynamic response analysis of TLP based on AQWA [J].Journal of Southeast University:Natural Science Edition,2009,39(supplement 2):304-310. |
| [11] |
冯定,方勇,王鹏,等.深水钻井平台与分段组合锚泊系统耦合分析[J].石油机械,2015,43(1):59-63. Feng Ding,Fang Yong,Wang Peng,et al.Analyses for coupling between deep-water semi-submersible drilling platform and sectional combined anchoring system[J].China Petroleum Machinery,2015,43(1):59-63. |
| [12] | API Recommended Practice 2SK.Recommended practice for design and analysis of station keeping systems for floating structures[S]. |
| [13] |
鞠少栋,畅元江,陈国明,等.深水钻井隔水管连接作业窗口分析[J].石油勘探与开发,2012,39(1):105-110. Ju Shaodong,Chang Yuanjiang,Chen Guoming,et al.Envelopes for connected operation of the deepwater drilling riser[J].Petroleum Exploration and Development,2012,39(1):105-110. |




