2. 大庆油田有限责任公司第一采油厂, 黑龙江大庆 163000
2. No.1 Oil Production Plant of Daqing Oilfield Company, Daqing, Heilongjiang, 163000, China
在钻井施工过程中,不仅要随时掌握钻头位置及井眼方向,还要与设计轨道进行对比,分析实钻轨迹与设计轨道的相符程度及其变化趋势,以便及时采取调整措施,确保中靶并保持良好的井身质量。此外,为了满足增加石油储量和产量的需求,老油田通过不断加密井网进行剩余油挖潜,非常规油气资源开发正在发展“井工厂”技术,海上钻井的单平台布井数量越来越多而形成高密集丛式井。随着布井密度的不断增大,邻井间的距离越来越小,因此邻井防碰问题就越来越突出。
法面扫描主要用于分析实钻轨迹与设计轨道的偏离程度,也用于邻井防碰的分析评价。这两种情况在技术方法上没有实质性的差异,都是采用法面扫描来分析井眼轨迹之间的相互位置关系。20世纪90年代,许多学者研究了法面扫描问题,基本形成了法面扫描的数值方法[1,2,3,4]。然而,近年来关于法面扫描的研究却再掀高潮[5,6,7],其主要原因是传统方法的缺陷开始凸显。目前,已经找到了一些解决方案,但依然存在一些不足之处。为此,研究提出了法面与比较井是否相交的判别方法和求解其交点的解析法,这些方法不需要对比较井进行插值计算,也不需要迭代计算,具有计算方法科学、计算过程高效、计算结果准确等优点。
1 传统方法的局限性为便于叙述两井间的相对位置关系,常把它们分别称之为参考井和比较井。参考井一般是新设计或是正在钻进的井,比较井是已设计或已钻成的邻井。事实上,无论是参考井还是比较井都既可以是设计轨道也可以是实钻轨迹,其计算方法本身与井眼轨迹的类型无关。法面扫描原理如图 1所示,即[1]:在参考井上选定一个参考点(P点),过该参考点作垂直于井眼轨迹切线的法平面,与比较井交于比较点(C点);当参考点沿参考井移动时,比较井上的比较点也随之变化。这样,就可以用参考点和比较点之间的距离等参数来表征两井间的相对位置关系。

|
| 图 1 法面扫描原理 Fig. 1 Principle of normal plane scanning |
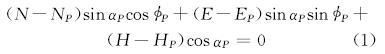
所以,如果定义:
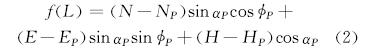
则比较点C应满足:

式中:N为北坐标,m;E为东坐标,m;H为垂深,m;L为井深,m;α为井斜角,(°);φ为方位角,(°);下标为各参数所对应的点。
当选定参考点后,参考点的轨迹参数(αP,φP,NP,EP,HP)就是已知参数,而比较井上任一点的坐标(N,E,H)是其井深的单变量函数,所以结合具体的井眼轨迹模型便可由式(3)确定比较点。
为判别法面是否与比较井相交,传统方法将比较井上各井段的两端点坐标依次代入式(2),并认为若满足式(4)则说明比较井段的两端点(A点和B点)分别位于法面两侧或法面上,此时法面必与比较井相交;否则,比较井段的两端点位于法面同侧,法面与比较井不相交,即此时不存在比较点。式(4)为:
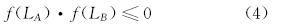
然而,这种判别方法并非普遍适用,在有些情况下会出现异常结果[5],从而导致遗漏井眼相碰的危险点。例如,当比较井段为空间圆弧时,即使A点和B点满足式(5),法面与比较井段仍可能有1个或2个交点(如图 2所示)。因此,传统的判别方法有局限性。式(5)为:

|
| 图 2 传统判别方法的异常情况分析 Fig. 2 Abnormal condition analysis of the conventional judgment method |
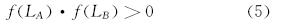
空间圆弧模型中,假设井眼轨迹是位于空间斜平面内的圆弧或直线。无论比较井段是圆弧段还是直线段,它与法面都存在平行或不平行两种情况,而比较井段与法面是否平行是判别比较点存在性的基础。由于参考点处井眼轨迹的切向量tP就是法面的法向量,所以法面的单位法向量为:
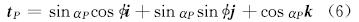
式中:i,j,k分别为N、E、H坐标轴上的单位坐标向量。
无论比较井段是设计轨道还是实钻轨迹,通常比较井段始点的轨迹参数都是已知数据。此外,对于设计轨道,比较井段的特征参数往往为已知数据;对于 实钻轨迹,比较井段的终点参数往往为已知数据。
当已知比较井段的特征参数时,比较井段始点的单位切向量tA和单位主法向量nA分别为:
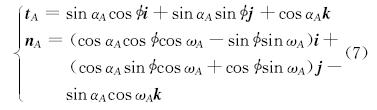
所以,若该圆弧段与法面平行,则应tP⊥tA且tP⊥nA。即:
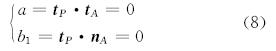
其中
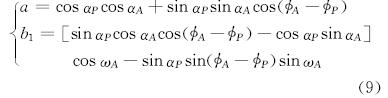
式中:ωA为比较井段始点的工具面角,(°)。
当已知比较井段的终点参数时,该圆弧段与法面平行的充分必要条件为:
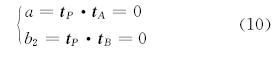
其中
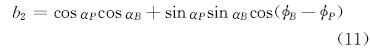
由于比较井段的特征参数与终点参数之间可以互算[7,8],所以式(8)和式(10)是等价的,实际应用时可取其一。例如,当比较井段为实钻轨迹时,可直接用式(10)来判别比较井段与法面是否平行;也可先算出比较井段的初始工具面角等参数,再用式(8)来判别比较井段与法面是否平行。
显然,当比较井段为直线段时,它与法面平行的充分必要条件退化为:
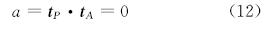
此外,为方便,令:

则c=0表明比较井段的始点位于法面内。
3 求解比较点的位置如果比较井段与法面相交,则存在比较点。比较点的位置可用比较点C与比较井段始点A之间的井深差ΔLAC来标识。如果比较井段为圆弧段,则有:
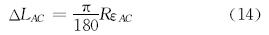
式中:εAC为比较点C与比较井段始点A之间的弯曲角,(°)。
当已知比较井段的特征参数时,εAC可表示为[7]:

当已知比较井段的终点参数时,εAC的计算公式为:
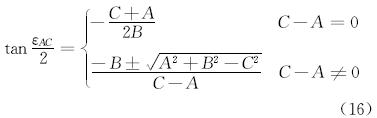
其中
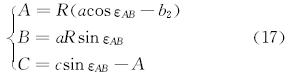
式中:εAB为比较井段A点和B点之间的弯曲角,(°)。
理论上,式(15)或式(16)会产生3种结果,即无解、有唯一解和有2个解,分别表明参考点法面与比较井段无交点、有1个交点和有2个交点。
如果比较井段为直线段,则有:
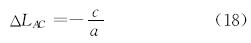
无论比较井段是直线段还是圆弧段,只有满足0≤ΔLAC≤ΔLAB才表明存在比较点。
4 法面扫描的技术流程首先,任一参考点法面可能会与比较井的多个井段相交(见应用实例),因此对于每个法面都必须扫描比较井的每个井段。当某个参考点法面与比较井的多个井段相交时,基于防碰考虑,应选取距离参考点最近者作为比较点。
对于一个参考点和一个比较井段,图 3给出了法面扫描的流程。在该流程中,首先计算a,b,c等参数。为方便,若比较井段为直线段,则令b=0(其中,b代表b1或b2)。若a=b=0,则说明比较井段平行于法面。此时,若再有c=0,则说明比较井段位于法面内,应选取比较井段上距离参考点最近的点作为比较点;否则,说明法面与比较井段不存在交点。若不满足a=b=0,则说明比较井段不平行于法面,此时用式(14)或式(18)来判别并求解比较点。 需要强调的是,只有当式(14)或式(18)有解且满足0≤ΔLAC≤ΔLAB时才存在比较点。

|
| 图 3 比较井段上是否存在比较点的判别流程 Fig. 3 Process to judge if a comparative point is available in comparison well section |
由于比较点C总是位于参考点P的法面内,所以可用这两点间的法面距离和扫描角来表征参考点P与比较点C之间的相对位置关系[7]:
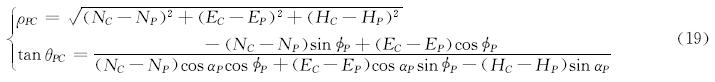
式中:ρPC为法面距离,m;θPC为扫描角,(°)。
这样,根据法面距离和扫描角就可以在极坐标系下绘制出法面扫描图。需要注意的是,扫描角θPC是指在参考点的法面上从参考点的井眼高边开始顺时针旋转至比较点C的角度。
5 应用实例假设新设计一口水平井,其设计轨道的节点数据见表 1。在该水平井310°方位线上550 m处,有一口已完钻井,其实钻轨迹的测点数据见表 2。为简便并体现出法面扫描方法的一般性和科学性,这两口井都假设为二维剖面且数据点稀疏。现以水平井为参考井,以已完钻井为比较井,进行法面扫描分析。
| 井深/m | 井斜角/(°) | 方位角/(°) | 北坐标/m | 东坐标/m | 垂深/m |
| 0 | 0 | 0 | 0 | 0 | |
| 1 360.00 | 0 | (0) | 0 | 0 | 1 360.00 |
| 1 540.00 | 42.00 | 0 | 63.07 | 0 | 1 524.31 |
| 1 685.00 | 42.00 | 0 | 160.10 | 0 | 1 632.06 |
| 1 820.00 | 86.00 | 0 | 278.47 | 0 | 1 689.80 |
| 2 380.00 | 86.00 | 0 | 837.11 | 0 | 1 728.86 |
| 井深/m | 井斜角/(°) | 方位角/(°) | 北坐标/m | 东坐标/m | 垂深/m |
| 0 | 0 | 0 | 0 | 0 | |
| 1 400.00 | 0 | (90.00) | 0 | 0 | 1 400.00 |
| 1 560.00 | 50.00 | 90.00 | 0 | 65.49 | 1 540.45 |
| 1 720.00 | 50.00 | 90.00 | 0 | 188.06 | 1 643.30 |
| 1 920.00 | 106.00 | 90.00 | 0 | 376.00 | 1 683.24 |
| 2 000.00 | 88.00 | 90.00 | 0 | 455.07 | 1 673.53 |
| 2 100.00 | 76.00 | 90.00 | 0 | 553.92 | 1 687.43 |
| 2 350.00 | 80.00 | 90.00 | 0 | 798.41 | 1 739.39 |
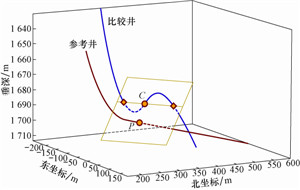
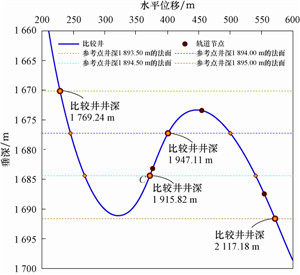
参考井和比较井的三维视图见图 4。在该实例中,有些参考点法面与比较井的多个井段相交,且对于满足式(5)的比较井段仍存在2个交点。例如,参考点井深为1 894.50 m 处的法面,与比较井的2个井段(1 720.00 m,1 920.00 m)和(2 000.00 m,2 100.00 m)相交;并且对于比较井段(1 720.00 m,1 920.00 m),不满足式(4)的条件,此时传统方法将误判为:法面与该比较井段不存在交点,而事实上存在2个交点。因此,该法面与比较井应共有3个交点,它们所对应的比较井井深分别为1 809.87、1 915.82和2 086.55 m,且在这3个交点中距离参考点最近者为井深1 915.82 m处的交点,即比较点的井深为1 915.82 m(如图 5所示)。但是,传统方法只能求得比较井井深为2 086.55 m的交点,从而导致计算结果错误。
|
| 图 4 参考井和比较井的三维视图 Fig. 4 3D views of reference wells and comparison wells |
|
| 图 5 不同法面与比较井的相交情况分析 Fig. 5 Analysis on intersection between different normal planes and comparison wells |
该实例的法面扫描结果见表 3和图 6。其中,图 6(b)中的曲线呈Z字形,是因为当法面沿参考井移动时,比较点将在比较井的不同井段间跳跃(见图 5)。
| 参考井 | 井间距离 | 比较井 | |||||||
| LP/m | αP/(°) | φP/(°) | ρPC//m | θPC /(°) | 高边距离/m | 右向距离/m | LC /m | αC/(°) | φC/(°) |
| 1 893.00 | 86.00 | 0 | 207.89 | 278.86 | 32.01 | -205.41 | 1 754.13 | 59.56 | 90.00 |
| 1 893.25 | 86.00 | 0 | 201.08 | 278.13 | 28.44 | -199.06 | 1 761.42 | 61.60 | 90.00 |
| 1 893.50 | 86.00 | 0 | 193.72 | 277.37 | 24.86 | -192.12 | 1 769.24 | 63.79 | 90.00 |
| 1 893.75 | 86.00 | 0 | 25.87 | 34.14 | 21.41 | 14.52 | 1 980.76 | 92.32 | 90.00 |
| 1 894.00 | 86.00 | 0 | 26.00 | 313.31 | 17.84 | -18.92 | 1 947.11 | 99.90 | 90.00 |
| 1 894.25 | 86.00 | 0 | 38.73 | 291.58 | 14.24 | -36.02 | 1 929.63 | 103.83 | 90.00 |
| 1 894.50 | 86.00 | 0 | 50.50 | 282.20 | 10.67 | -49.36 | 1 915.82 | 104.83 | 90.00 |
| 1 894.75 | 86.00 | 0 | 65.98 | 276.16 | 7.08 | -65.60 | 1 899.18 | 100.17 | 90.00 |
| 1 895.00 | 86.00 | 0 | 149.31 | 88.66 | 3.50 | 149.27 | 2 117.18 | 76.27 | 90.00 |
| 1 895.25 | 86.00 | 0 | 164.13 | 90.03 | -0.09 | 164.13 | 2 132.47 | 76.52 | 90.00 |
| 1 895.50 | 86.00 | 0 | 179.26 | 91.17 | -3.67 | 179.22 | 2 147.97 | 76.77 | 90.00 |

|
| 图 6 应用实例的法面扫描图 Fig. 6 Normal plane scanning diagram of application examples |
正如引言中所述,实钻轨迹偏离程度分析和邻井防碰评价在技术方法上没有实质性的差异。所以,该实例主要用于验证比较点存在性的判别方法和求解比较点的解析法,从而完善分析井眼轨迹间相互位置关系的法面扫描法。实际上,还可以用更为简明而高效的实例来初步验证法面扫描解析算法的正确性。例如,若假设参考井为直井,则法面将变为水平面,此时笔者给出的方法及公式仍适用,但计算过程大为简化。
6 结 论1) 当比较井段不平行于法面时,无论比较井段的两端点位于法面的同侧还是异侧,比较井段都有可能与法面相交。此时,无需考虑比较井段两端点位于法面的同侧或异侧问题,可直接求解比较井段与法面的交点,若有解且该交点位于比较井段内,就存在比较点。
2 ) 基于井眼轨迹的空间圆弧模型,得到了比较井段与法面交点的解析算法,具有计算过程高效、计算结果准确等优点。
3) 任一参考点法面可能会与比较井的多个井段相交,因此对于每个法面都必须扫描比较井的每个井段。当某个参考点法面与比较井的多个井段相交时,基于防碰考虑应选取距离参考点最近者作为比较点。
| [1] | Thorogood J L,Sawaryn S J.The traveling-cylinder diagram:a practical tool for collision avoidance[J].SPE Drilling Engineering,1991,6(1):31-36. |
| [2] |
韩志勇,宁秀旭.一种新的定向钻井绘图:法面扫描图[J].石油大学学报:自然科学版,1990,14(3):24-30. Han Zhiyong,Ning Xiuxu.A new plotting for directional drilling:normal-plane-sanning chart[J].Journal of the University of Petroleum,China:Natural Science Edition,1990,14(3):24-30. |
| [3] |
高德利,韩志东.邻井距离扫描计算与绘图原理[J].石油钻采工艺,1993,15(5):21-29. Gao Deli,Han Zhidong.Calculation and drawing principle for adjacent well distance scanning[J].Oil Drilling & Production Technology,1993,15(5):21-29. |
| [4] |
刘修善,岑章志.井眼轨迹间相互关系的描述与计算[J].钻采工艺,1999,22(3):7-12. Liu Xiushan,Cen Zhangzhi.Description and calculation of relative positions of wellbore trajectories[J].Drilling & Production Technology,1999,22(3):7-12. |
| [5] |
夏泊洢.邻井法面距离计算方法的改进[J].石油地质与工程,2012,26(5):113-116. Xia Boyi.Perfection of calculating normal plane distance between wells[J].Petroleum Geology and Engineering,2012,26(5):113-116. |
| [6] |
唐雪平.一种精确的井距计算方法[J].数学的实践与认识,2012,42(17):69-78. Tang Xueping.An exact well distance calculation method[J].Mathematics in Practice and Theory,2012,42(17):69-78. |
| [7] |
刘修善.一种井间相对位置关系的法面扫描解析方法:中国,201410199045.6[P].2014-05-12. Liu Xiushan.Analytical method for normal plane scanning of relative position between wells:CN,201410199045.6[P].2014-05-12. |
| [8] |
刘修善,王超.空间圆弧轨迹的解析描述技术[J].石油学报,2014,35(1):134-140. Liu Xiushan,Wang Chao.Analytic description of spatial-arc wellbore trajectory[J].Acta Petrolei Sinica,2014,35(1):134-140. |




