页岩油气资源分布广、储量大但丰度低,需进行大型体积压裂才能达到商业开采目的[1,2]。由于页岩中存在大量天然裂缝,导致人工裂缝的扩展方向及体积压裂规模难以控制和估计,因此研究页岩破裂过程中裂纹之间的相互作用具有重要意义。
对于岩石细观力学变形,主要采用的是PFC方法,该方法是P.A.Cundall等人[3]在离散元理论基础上提出的,用来模拟颗粒的运动以及颗粒与颗粒之间应力的交互作用。M.Bahaaddini等人[4]运用PFC方法研究了节理几何参数对岩体破裂机制、单轴抗压强度和变形模量的影响;Zhang Xiaoping等人[5]运用PFC方法研究了岩体在单轴压缩下预制裂纹的演化扩展过程;王连庆等人[6]利用PFC方法研究了自然崩落矿体的崩落规律;周健等人[7]运用PFC方法对砂性土坡和黏性土坡分别进行了数值模拟,还对岩体中存在流体流动时的渗流现象进行了颗粒流的细观模拟[8];孙峰等人[9]运用PFC方法对土体劈裂注浆过程进行了细观模拟研究;杨艳等人[10]利用PFC方法研究了裂隙岩体水力劈裂过程。但是,以上研究均仅考虑了层理或单裂隙下岩体的变形,没有考虑多裂纹条件下岩体的变形特性以及裂纹之间的相互作用。
采用PFC方法,首先需要确定岩体的细观力学参数。针对页岩岩体,笔者采用并行PSO算法反演了页岩颗粒模型的细观力学参数,并在此基础上进行了含2条裂纹的巴西劈裂试验,分析了裂纹演化扩展规律,最后考虑流固耦合进行了含2条裂纹的水力劈裂试验,分析了影响劈裂纹扩展的因素。
1 页岩颗粒模型颗粒流采用数值方法将物体分为有代表性的颗粒单元,通过离散单元方法来模拟圆形颗粒介质的运动及其相互作用,期望利用局部的模拟结果来研究颗粒介质的本构模型。对页岩破裂的研究,需要先建立起页岩的颗粒模型,然后再进行其他各种试验。
1.1 宏观力学参数页岩储层岩石基质致密、渗透率低,其力学性质与一般砂岩、碳酸盐岩相比具有一定的特殊性。有关页岩岩石力学参数测定的论文已发表很多,笔者采用文献[11]中的试验结果,且选择垂直页理方向上的数据:岩石的密度为2 532 kg/m3,弹性模量为35.68 GPa,泊松比为0.257,单轴抗压强度为200.3 MPa。该组参数反映了典型页岩的力学特性。
1.2 细观力学参数反演岩石宏观力学参数与细观力学参数之间存在非线性关系,两者之间的关系无法用确切的数学表达式表示。目前,细观力学参数的选取大都采用反复试验的方法,对经验的依赖性强,且调试的颗粒参数较多,需耗费大量的时间。针对颗粒流的接触黏结和平行黏结两种模型,笔者采用并行PSO算法快速反演了页岩细观力学参数,结果见表 1。以反演的细观力学参数作为输入条件模拟获得宏观力学参数,结果见表 2(真实值取自“1.1宏观力学参数”)。由表 2可知,模拟值与真实值之间的误差很小,相对误差皆小于1.6%,从而可以在此基础上进行页岩相关数值试验。
| 模型 |
颗粒弹性模
量/GPa |
法向和切
向刚度比 |
黏结弹性模
量/GPa |
摩擦
系数 |
黏结强
度/GPa |
| 接触黏结 | 52.1 | 2.365 | 1.111 | 0.167 | |
| 平行黏结 | 11.7 | 2.430 | 40.6 | 1.963 | 0.172 |
| 模型 | 数据类别 |
弹性模量/
GPa | 泊松比 |
单轴抗压
强度/GPa |
| 真实值 | 35.68 | 0.257 0 | 0.200 3 | |
| 接触黏结 | 模拟值 | 35.62 | 0.259 0 | 0.201 0 |
| 平行黏结 | 模拟值 | 35.64 | 0.261 0 | 0.201 0 |
页岩中存在页理,使大部分页岩都呈现出明显的各向异性,笔者拟研究裂纹之间扩展的相互作用,所以将页岩模型作简化处理,不考虑页理的影响。
基于页岩颗粒模型,进行预制裂纹巴西劈裂数值试验,岩样如图 1所示。岩样直径为50 mm,颗粒最小半径为0.275 mm,粒径比为1.66。岩样中含2条预制裂纹,裂纹之间的夹角为β,裂纹长度分别为l1和l2。预制裂纹是通过删除自定义范围内的颗粒形成的,l1=10.0 mm,l2=14.2 mm。分析了夹角β为30°,45°和90°时的裂纹演化扩展情况以及应力-应变曲线特征。
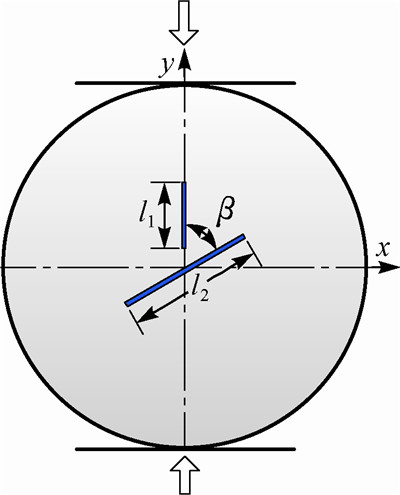
|
| 图 1 岩样形状 Fig.1 Geometry of rock specimen |
图 2—图 4分别为裂纹夹角30°,45°和90°岩样加载计算所得的破坏形态。

|
| 图 2 裂纹夹角30°岩样的破坏形态 Fig.2 Fracture morphology of rock specimen when β=30° |

|
| 图 3 裂纹夹角45°岩样的破坏形态 Fig.3 Fracture morphology of rock specimen when β=45° |

|
| 图 4 裂纹夹角90°岩样的破坏形态 Fig.4 Fracture morphology of rock specimen when β=90° |
由图 2可知,β为30°时垂直裂纹先沿着y方向向两边扩展,当下端裂纹扩展到倾斜裂纹时停止扩展,倾斜裂纹两端裂纹开始扩展,上端裂纹沿着裂纹方向扩展然后沿着y方向扩展,下端裂纹沿着y方向扩展,直至岩样边端。
由图 3可知,β为45°时垂直裂纹下端裂纹扩展至倾斜裂纹时停止扩展,倾斜裂纹两端裂纹开始扩展,上端裂纹沿着x方向扩展至岩样边端,下端演化出2条裂纹,沿着原裂纹方向扩展然后沿着y方向扩展至岩样边端。
由图 4可知,β为90°时垂直裂纹先沿着y方向向两边扩展,下端裂纹扩展至水平裂纹时穿过水平裂纹往下继续扩展,直至岩样边端;当预制裂纹夹角较小时,倾斜裂纹会阻止垂直裂纹扩展,倾斜裂纹两端出现新的裂纹,且β为45°时裂纹的演化扩展较为复杂,当预制裂纹夹角较大时,垂直裂纹会贯穿倾斜裂纹扩展。
综合图 2—图 4可知,预制裂纹之间的夹角不同,裂纹的演化扩展情况不同。
2.2 应力-应变曲线预制裂纹的存在会影响其破坏形态,并影响岩石的力学行为。不同裂纹夹角下的岩样应力-应变曲线如图 5所示。
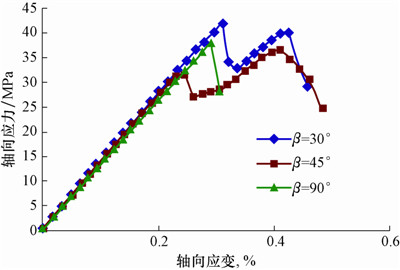
|
| 图 5 应力-应变曲线 Fig.5 Stress-strain curve |
由图 5可知:当预制裂纹的夹角不同时,岩样的峰值强度不同且应力-应变形态不同;β为45°时岩样峰值强度最小,β为90°时岩样峰值强度次之,β为30°时岩样峰值强度最大;β为90°时岩样从发生变形直至破坏都属于弹性变形;而β为30°和45°时岩样先为弹性变形,达到峰值强度之后开始塑性变形,裂纹演化扩展至岩样边端。
3 水力劈裂试验利用颗粒离散元流固耦合原理可以进行页岩水力劈裂试验。假设流体的渗流路径由颗粒间接触处的平行板通道组成,域单元可以存储流体压力,通过流量和压力的计算模拟流体在颗粒之间的流动。
建立的预制裂纹岩体水力劈裂计算模型如图 6所示。数值试验通过伺服机制控制墙体速度,使模型y方向和x方向边界分别产生σ1和σ2的应力。与前一模型相同,在该模型中预制了夹角为β的2条裂纹,不同之处是该模型将相应区域内颗粒间的接触黏结强度设为一个很小值,而不删除区域内颗粒。
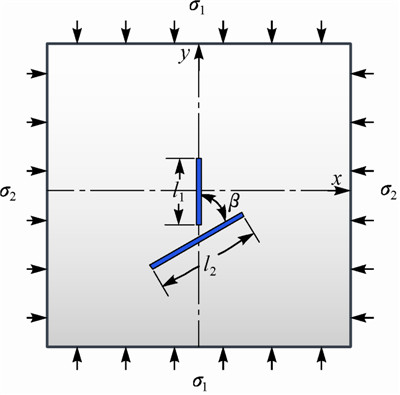
|
| 图 6 预制裂纹岩体水力劈裂计算模型 Fig.6 Model of hydraulic fracturing of rock with preset cracks |
流体计算参数的选择对流体压力的变化有重要影响,因而也影响裂纹的演化扩展。为保证计算值相对稳定,选择较小的时间步长。流体计算参数取值:残余孔径1.0×10-3 m,渗透系数1.0×10-15 m/s,流体体积模数1.0×109 Pa,法向压力1.0×106 N,距离缩放因子0.2,表观体积2.0×10-6 m3,时间步长0.05 s。开始模拟水力劈裂时,在垂直裂纹范围内施加全水头荷载,观察裂纹在该水力作用下的演化扩展以及与倾斜裂纹之间的相互作用。
边界应力σ1=4.5 MPa和σ2=3.5 MPa时,模拟了β为30°,45°,90°时裂纹的演化扩展过程,如图 7—图 9所示(红色表示法向张裂纹,蓝色表示切向剪裂纹)。

|
| 图 7 裂纹夹角为30°时水力劈裂后的裂纹形态 Fig.7 Fracture morphology after hydraulic fracturing when β=30° |

|
| 图 8 裂纹夹角为45°时水力劈裂后的裂纹形态 Fig.8 Fracture morphology after hydraulic fracturing when β=45° |
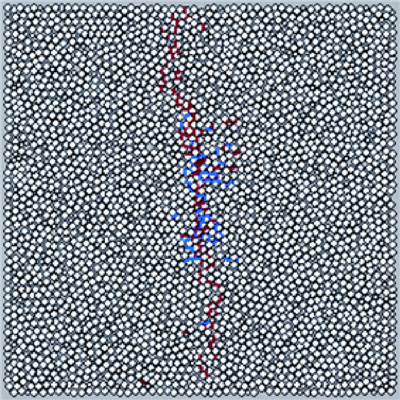
|
| 图 9 裂纹夹角为90°水力劈裂后的裂纹形态 Fig.9 Fracture morphology after hydraulic fracturing when β=90° |
由图 7、图 8可知,当预制裂纹夹角为30°和45°时,垂直裂纹沿y方向向两边扩展,下端裂纹与倾斜裂纹相交时,倾斜裂纹发生剪切破坏产生剪裂纹,随着水的继续注入,倾斜裂纹的下端开始产生张裂纹,并且沿y方向扩展至岩样边端,而倾斜裂纹的上端没有产生裂纹。
为了考虑应力差对裂纹扩展行为的影响,在倾斜角为45°的情况下模拟了应力差分别为1和7 MPa时的裂纹扩展形态,如图 8所示。由图 8可知,相比于低应力差条件,高应力差条件下形成的裂纹扩展方向比较集中,不至于分散,且垂向裂纹转向倾斜裂纹之后,倾斜裂纹下端能够较快地形成张裂纹,且张裂纹沿垂直方向扩展。
由图 9可知,当预制裂纹之间的夹角为90°时,垂直裂纹沿y方向向两边扩展,水平裂纹发生剪切破坏产生剪裂纹,垂直裂纹穿过水平裂纹继续扩展直至岩样边端。
试验结果表明:预制裂纹之间的夹角越小,倾斜裂纹越容易发生剪切破坏,垂直裂纹越趋于改变扩展方向,扩展路径越复杂;预制裂纹之间的夹角越大,倾斜裂纹对垂直裂纹的影响越小,垂直裂纹越容易贯穿倾斜裂纹进行扩展。
根据上述模型,采用Fracod2D模型[12]对裂纹夹角为90°时的扩展进行了模拟,结果如图 10所示。
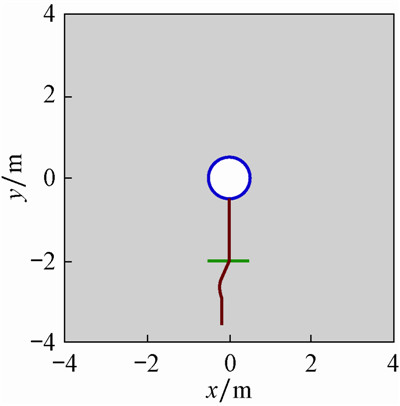
|
| 图 10 采用Fracod2D模型模拟的结果 Fig.10 Simulation results using Fracod2D Model |
图 9与图 10都表明,垂向裂纹贯穿了水平裂纹,同时也证明了PFC方法的正确性。
由于页岩储层中含有大量天然裂缝,页岩油气藏压裂时往往形成复杂的裂缝网络,而不是单条裂缝,其主要原因就是天然裂缝会发生剪切破坏,水力裂缝发生转向扩展。上述模型的模拟结果与实际压裂结果具有相同的规律,可见两者所反映的破坏机理相似,因此可利用PFC方法进行多裂隙岩体水力劈裂研究。
4 结 论1) 根据页岩宏观力学参数,采用并行PSO算法能快速准确地反演出页岩颗粒流模型的细观力学参数,该方法也可用来反演页岩的其他参数。
2 ) 页岩巴西劈裂试验裂纹之间的夹角越小,裂纹扩展越容易转向,变形越趋于塑性变形,裂纹间的相互作用越明显。
3) 页岩水力劈裂试验裂纹之间的夹角越小,裂纹越容易发生剪切破坏,裂缝越趋于改变扩展方向,扩展路径也越复杂,且应力差越小,裂纹扩展路径越复杂。
4 ) 天然裂缝的倾角和地应力差对最终裂缝网 络的形态具有重要作用,会对页岩气井压裂后的产能产生影响。
| [1] |
姚军, 孙海, 黄朝琴, 等.页岩气藏开发中的关键力学问题[J].中国科学:物理学 力学 天文学, 2013, 43(12):1527-1547. Yao Jun, Sun Hai, Huang Zhaoqin, et al.Key mechanical problems in the development of shale gas reservoirs[J].Scientia Sinica:Physica, Mechanica & Astronomica, 2013, 43(12):1527-1547. |
| [2] |
邵尚奇, 田守嶒, 李根生, 等.泥页岩地层水力裂缝延伸方位研究[J].石油钻探技术, 2014, 42(3):27-31. Shao Shangqi, Tian Shouceng, Li Gensheng, et al.Propagating orientation of hydraulic fractures in muddy shale formation[J].Petroleum Drilling Techniques, 2014, 42(3):27-31. |
| [3] | Cundall P A, Strack O D L.Particle flow code in 2 dimensions[M].Minnesota:Itasca Consulting Group Inc, 1999:1-15. |
| [4] | Bahaaddini M, Sharrock G, Hebblewhite B K.Numerical investigation of the effect of joint geometrical parameters on the mechanical properties of a non-persistent jointed rock mass under uniaxial compression[J].Computers and Geotechnics, 2013, 49:206-225. |
| [5] | Zhang Xiaoping, Wong Louis Ngai Yuen.Cracking processes in rock-like material containing a single flaw under uniaxial compression:a numerical study based on parallel bonded-particle model approach[J].Rock Mechanics and Rock Engineering, 2012, 45(5):711-737. |
| [6] |
王连庆, 高谦, 王建国, 等.自然崩落采矿法的颗粒流数值模拟[J].北京科技大学学报, 2007, 29(6):557-561. Wang Lianqing, Gao Qian, Wang Jianguo, et al.Numerical simulation of natural caving method based on particle flow code in two dimensions[J].Journal of University of Science and Technology Beijing, 2007, 29(6):557-561. |
| [7] |
周健, 王家全, 曾远, 等.土坡稳定分析的颗粒流模拟[J].岩土力学, 2009, 30(1):86-90. Zhou Jian, Wang Jiaquan, Zeng Yuan, et al.Simulation of slope stability analysis by particle flow code[J].Rock and Soil Mechanics, 2009, 30(1):86-90. |
| [8] |
周健, 张刚, 孔戈.渗流的颗粒流细观模拟[J].水利学报, 2006, 37(1):28-32. Zhou Jian, Zhang Gang, Kong Ge.Meso-mechanics simulation of seepage with particle flow code[J].Journal of Hydralic Engineering, 2006, 37(1):28-32. |
| [9] |
孙锋, 张顶立, 陈铁林, 等.土体劈裂注浆过程的细观模拟研究[J].岩土工程学报, 2010, 32(3):474-480. Sun Feng, Zhang Dingli, Chen Tielin, et al.Meso-mechanical simulation of fracture grouting in soil[J].Chinese Journal of Geotechnical Engineering, 2010, 32(3):474-480. |
| [10] |
杨艳, 常晓林, 周伟, 等.裂隙岩体水力劈裂的颗粒离散元数值模拟[J].四川大学学报:工程科学版, 2012, 44(5):78-85. Yang Yan, Chang Xiaolin, Zhou Wei, et al.Simulation of hydraulic fracturing of fractured rock mass by PFC2D[J].Journal of Sichuan University:Engineering Science Edition, 2012, 44(5):78-85. |
| [11] |
杨建, 付永强, 陈鸿飞, 等.页岩储层的岩石力学特性[J].天然气工业, 2012, 32(7):12-14. Yang Jian, Fu Yongqiang, Chen Hongfei, et al.Rock mechanical characteristics of shale reservoirs[J].Natural Gas Industry, 2012, 32(7):12-14. |
| [12] | Shen B, Stephansson O, Rinne M, et al.Fracod modeling of rock fracturing and permeability change in excavation damaged zones[J].International Journal of Geomechanics, 2010, 11(4):302-313. |





