2. 东北石油大学石油工程学院, 黑龙江大庆 163318
2. College of Petroleum Engineering, Northeast Petroleum University, Daqing, Heilongjiang, 163318, China
水平井多级压裂能增加泄油气面积、提高储层动用程度和单井产量,是低渗透致密砂岩气藏开发的核心技术之一[1,2,3,4,5,6,7,8,9]。致密砂岩油气藏中常发育有天然裂缝,在压裂过程中,天然裂缝在压裂压力作用下开启,使水力裂缝转向,形成复杂裂缝[10,11,12]。复杂裂缝的形成与地应力状态、压裂过程中的诱导应力和压裂压力有关[13,14]。 T.L.Blanton等人[15,16,17]研究了天然裂缝的受力状态和破坏方式,考虑天然裂缝走向和倾角对水力裂缝开启的影响,建立了水力裂缝起裂压力计算模型;邵尚奇等人[18]研究了天然裂缝对水力裂缝走向的影响;L.J.L.Beugelsdijk等人[19,20,21]通过物理模拟,得到了天然裂缝对水力裂缝扩展及裂缝形态的影响。但以上研究都没有考虑多级压裂过程诱导应力对天然裂缝开启的影响。
水平井多级压裂时,由于先压开裂缝诱导应力的作用,后压裂区域的地应力状态发生改变,对天然裂缝的开启产生影响。笔者建立了考虑诱导应力的地应力分布计算模型和天然裂缝发生张性破坏和剪切破坏开启的判别模型,明确了诱导应力对地应力的影响规律,得到天然裂缝的开启规律,为合理设计压裂压力、提高压裂效果提供了理论依据。
1 压裂水平井井壁围岩应力分布压裂过程中,井眼附近出现应力集中现象,在原始地应力、井眼内压力作用下的井壁应力表达式为[22]:

式中:R为井眼半径,m;r为井眼围岩任意点离开井轴中心的距离,m;θ为井眼围岩任意点与井眼中心连线偏离垂直方向的夹角,(°);pw为井眼内液柱压力,MPa;ν为井壁岩石泊松比;σr0,σθ0,σz0,τrθ0,τθz0和τzr0为柱坐标系下井筒周围地应力分量,MPa;σxx,σyy,σzz,τxy,τyz和τzx为地应力转换分量,可以根据水平主应力 σH和σh,垂向地应力σv及井筒方位角等参数的转换计算得到,MPa。
2 压裂储层应力分布 2.1 压裂过程诱导应力分析压裂时,近井地带水力裂缝的扩展对附近地层产生诱导应力作用,根据弹塑性力学理论,假设地层岩石为均质、各向同性材料,以二维平面应变模型为基础,建立几何模型(见图 1),设第n条裂缝半缝高为hn。定义拉应力为正,压应力为负。
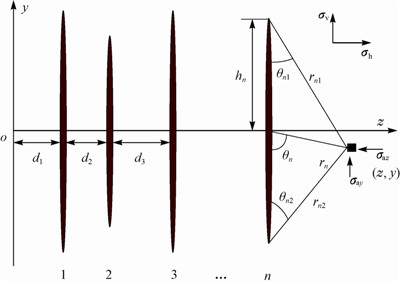
|
| 图 1 二维垂直裂缝段间诱导应力场示意 Fig. 1 Induced stress field between two-dimensional vertical fractures |
第n条水力裂缝在zy平面内裂缝周围质点(z,y)处产生的诱导应力为:

式中:σaxn,σayn和σazn为先压开第n条裂缝产生的诱导应力正应力分量,MPa;τazyn先压开第n条裂缝产生的诱导应力剪切应力分量,MPa;pn为第n条裂缝内的流体净压力,MPa;rn,rn1和rn2分别为垂直裂缝中部、顶端和底端到质点的距离,m;θn,θn1和θn2分别为垂直裂缝中部、顶端和底端到质点的直线与裂缝面的夹角,(°)。
式(2)中,各几何参数间存在以下关系:

式中:d1为第一条裂缝与y轴的距离,m;di为第i(i=2,3,…,n)条裂缝与i-1条裂缝的距离,m。
根据弹性力学叠加原理,全部n条先压裂缝在质点(z,y)处产生的总诱导应力可表示为:
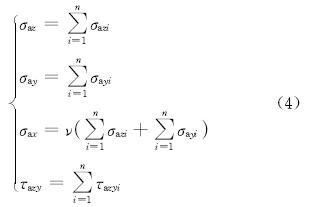
式中:σax、σay和σaz为先压全部n条裂缝产生的总诱导应力正应力分量,MPa;τazy为先压全部n条裂缝产生的总诱导应力剪切应力分量,MPa。
2.2 压裂过程地应力计算压裂过程中,由于压裂液和先压裂缝诱导应力的作用,地层的地应力状态发生改变,地层应力场是在原始地应力、井筒围岩应力和裂缝诱导应力共同作用下形成的,根据弹性力学叠加原理,在以水平井井筒方向为z轴的极坐标系中,该地应力可以表示为:
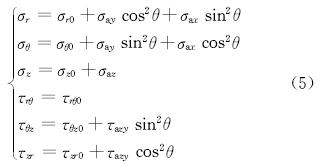
式中:σr,σθ,σz,τrθ,τθz和τzr为考虑诱导应力的地应力分量,MPa。
根据式(5),可以计算出压裂过程中受压裂液和先压裂缝诱导应力影响的地应力分布情况。
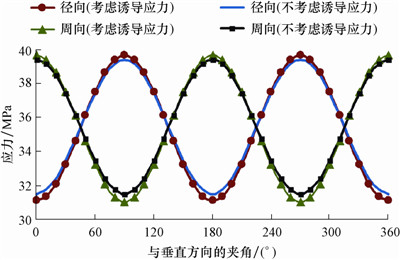
2.3 诱导应力对地应力影响分析黑185井是吉林油田某区块的一口多级压裂水平井,共压裂7段,该区块的地应力、岩石力学参数和该井的参数如下:最大水平主应力σH=39.43 MPa,最小水平主应力σh=26.16 MPa,垂向地应力σv=31.5 MPa,井眼半径R=0.113 35 m,压裂时井内液柱压力pw=42.60 MPa,地层岩石泊松比ν=0.24,井斜角α=90°,方位角Φ=188.54°,裂缝半缝高hn=30 m,裂缝内的流体净压力pn=4.25 MPa。将基础数据代入模型中,可以求出压裂第7段时,考虑诱导应力和不考虑诱导应力的地应力分布情况(见图 2—图 4)。其中,不考虑诱导应力影响时,图 4中的剪切应力应为0 MPa。
|
| 图 2 径向应力和周向应力分布曲线 Fig. 2 Distribution of radial and circumferential stresses |
|
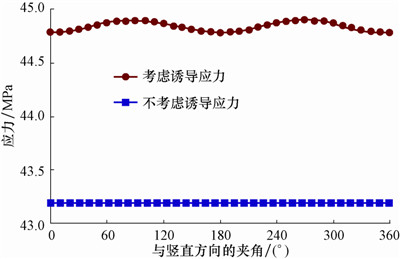
| 图 3 井筒轴线方向应力分布曲线 Fig. 3 Distribution of stress along the wellbore direction |
|
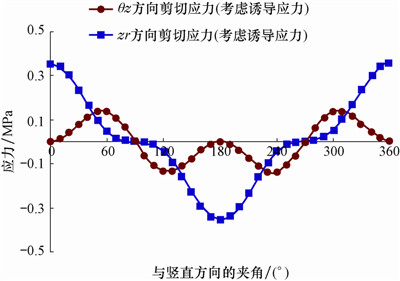
| 图 4 考虑诱导应力的剪切应力分布曲线 Fig. 4 Distribution of shear stress(which is 0 if the induced stress is not considered) |
由图 2—图 4可以看出:考虑诱导应力与不考虑诱导应力时井壁径向应力、周向应力和轴向应力都呈正弦(或余弦)规律变化。考虑诱导应力时径向应力最大值增大了0.3 MPa,最小值增大了-0.4 MPa;周向应力最大值增大了0.29 MPa,最小值增大了-0.46 MPa;轴向应力最大值增大了1.71 MPa,最小 值增大了1.60 MPa;θz方向剪应力增大了0.14 MPa;zr方向剪应力增大了0.36 MPa。以上分析表明,诱导应力对周向应力和径向应力的影响较小,对轴向应力和剪切应力的影响较大,在分析天然裂缝开启规律时要考虑诱导应力对地应力的影响。
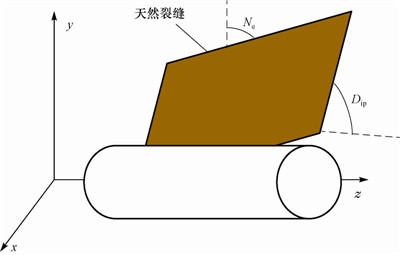
3 天然裂缝开启规律研究 3.1 天然裂缝受力状态分析图 5表示了井筒附近天然裂缝分布情况。
|
| 图 5 井筒附近天然裂缝分布情况 Fig. 5 Distribution of natural fractures near the borehole |
为了分析天然裂缝的受力情况,首先建立空间坐标系(见图 5),在大地坐标系(N,E,D)中,天然裂缝走向为北偏东Ne,天然裂缝倾角为Dip。在大地坐标系下天然裂缝的法向矢量为:
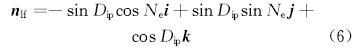
式中:nlf为天然裂缝的法向矢量。
在水力裂缝与天然裂缝交点处,地应力分量分 别为σr,σθ,σz,τrθ,τθz和τzr。根据弹塑性力学理论,可以计算出该应力条件下的3个应力不变量为:
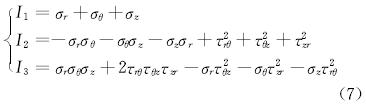
式中:I1,I2和I3分别为第一、第二和第三应力不变量。
根据式(7)求得第一、第二和第三应力不变量后,将各应力不变量代入式(8),可求得相应主应力σ1,σ2和σ3的大小。

相应各主应力的方向,可以通过下式求得:

式中:li1,li2和li3分别为第一、第二和第三主应力的方向余弦。
在式(9)中分别代入主应力,可计算出各主应力的方向余弦li1、li2和li3。所以,各主应力与裂缝面法线夹角的余弦为:
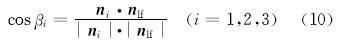
其中
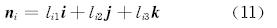
式中:βi为第i主应力与裂缝面的夹角,(°);ni为第i主应力的方向失量。
天然裂缝与水力裂缝交点处裂缝受到的正应力为:
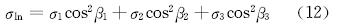
式中:σln为水力裂缝与天然裂缝交点处天然裂缝承受的正应力,MPa。
3.2 天然裂缝开启的力学条件水力裂缝与天然裂缝相交后,天然裂缝在流体压力作用下发生张性或剪切破坏而延伸,形成复杂裂缝,下面从天然裂缝的张性破坏和剪切破坏2方面进行力学分析。
3.2.1 天然裂缝张性开启力学条件水力裂缝与天然裂缝交点处水力裂缝内流体压力达到或大于作用于天然裂缝面的有效应力,使天然裂缝发生张性断裂,天然裂缝张性开启,其力学条件为:
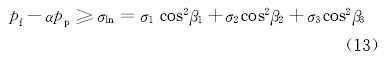
式中:pf为水力裂缝与天然裂缝交点处水力裂缝内流体压力,MPa;α为孔隙压力系数;pp为孔隙压力,MPa。
3.2.2 天然裂缝剪切破坏力学条件相对于地层岩石,天然裂缝可以看成是力学性质薄弱的结构弱面,因此,当作用于天然裂缝的剪切应力大于裂缝本身的抗剪切强度时,天然裂缝发生剪切破坏,其力学条件为:
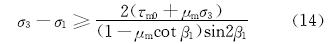
式中:τm0为天然裂缝内岩石粘聚力,MPa;μm为天然裂缝的内摩擦系数。
通过上述天然裂缝张性开启和剪切破坏的力学条件,即可判断和确定水平井多级压裂过程天然裂缝是否开启并形成复杂裂缝。
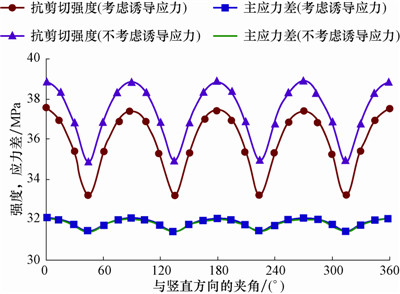
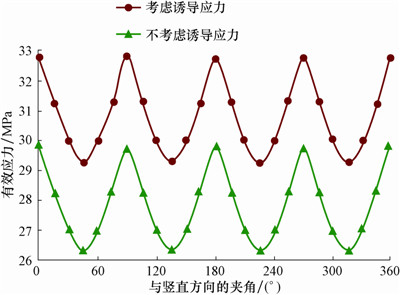
4 现场应用与计算结果分析黑185井所在区块储层平均孔隙度15.78%、渗透率27.1 mD,裂缝发育,属于致密砂岩油藏。该井采用双封拖动多级压裂工艺,共压裂7段。根据地质资料及取心岩样观察,天然裂缝的倾角为80°~120°,走向北偏东30°~65°。天然裂缝内岩石粘聚力τm0=11.7 MPa,天然裂缝的内摩擦系数μm=0.24。根据所建立的模型计算该区块的裂缝开启情况,其他计算参数与2.3中的参数一致,计算结果如图 6和图 7所示。
|
| 图 6 天然裂缝主应力差值与抗剪强度随井周角变化曲线 Fig. 6 Variation of principal stress difference and shearing strength of natural fractures with the well circumferential angle |
|
| 图 7 天然裂缝有效应力随井周角变化曲线 Fig. 7 Variation of effective stress of natural fractures with the well circumferential angle |
由图 6可以看出,考虑诱导应力影响和不考虑诱导应力影响时,天然裂缝内岩石所受的剪应力小于岩石的抗剪强度,在该地应力条件下,天然裂缝不会发生剪切破坏而开启,应考虑天然裂缝发生张性破坏开启。
从图 7可以看出,考虑诱导应力影响的天然裂缝岩石所受的有效应力要大于不考虑诱导应力影响 时岩石所受的有效应力。有效应力在与竖直方向夹 角为45°时取得最小值,考虑诱导应力影响的有效应力最小值为29.27 MPa;不考虑诱导应力影响的有效应力最小值为26.31 MPa。根据压裂设计方案,该段设计压裂压力为26.54MPa,实际施工时地面泵压是27.68 MPa,施工泵压高于设计压力。压裂时的微地震监测结果如图 8所示,由图 8可以看出,该段压裂时产生的是单一裂缝,天然裂缝没有开启形成复杂裂缝。根据计算结果,需要将地面泵压提高至29.27 MPa,才能使天然裂缝开启,产生复杂裂缝。
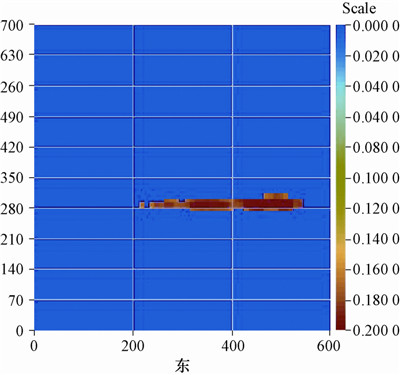
|
| 图 8 第七段裂缝分布微地震监测结果 Fig. 8 Fractures distribution in the 7th stage from micro-seismic |
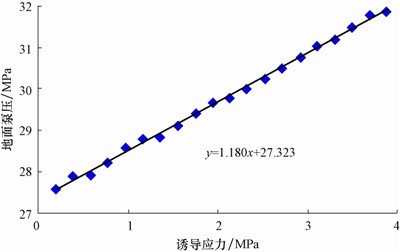
诱导应力和天然裂缝开启所需地面泵压之间的关系曲线如图 9所示。
|
| 图 9 诱导应力与天然裂缝开启所需地面泵压的关系曲线 Fig. 9 Relationship between induced stress and the pump pressure required to activate natural fractures |
从图 9可以看出,随着诱导应力的增大,天然裂缝开启所需的地面泵压增大,二者呈线性关系,直线的斜率为1.18,即多级压裂过程中产生1.00 MPa的诱导应力,天然裂缝开启变得困难,为了使天然裂缝开启,需要将地面泵压至少提高1.18 MPa。进行压裂设计时,为了形成复杂裂缝,应考虑诱导应力的影响。
5 结 论1) 多级压裂诱导应力对天然裂缝开启有重要影响,诱导应力对周向应力和径向应力的影响较小,对沿井筒方向的应力和剪切应力的影响较大,诱导应力使沿井筒方向的应力大幅增大。
2 ) 通过分析天然裂缝受力状态,建立了考虑诱导应力影响的天然裂缝发生张性破坏和剪切破坏开启的力学模型。
3) 诱导应力使天然裂缝开启变得困难,诱导应力增大,天然裂缝开启所需的地面泵压线性增大。如何计算不同地应力下考虑诱导应力时天然裂缝开启所需提高的地面泵压,是今后的研究重点。
| [1] |
张应安.松辽盆地致密砂岩气藏水平井多级压裂现场实践:以长深D平2井为例[J].天然气工业, 2011, 31(6):46-48. Zhang Ying'an.Multi-stage frac treatment in horizontal wells of tight sandstone gas reservoir in the Songliao Basin:a case history of the horizontal well Changshen D2[J].Natural Gas Industry, 2011, 31(6):46-48. |
| [2] |
唐颖, 张金川, 张琴, 等.页岩气井水力压裂技术及其应用分析[J].天然气工业, 2010, 30(10):33-38. Tang Ying, Zhang Jinchuan, Zhang Qin, et al.An analysis of hydraulic fracturing technology in shale gas wells and its application[J].Natural Gas Industry, 2010, 30(10):33-38. |
| [3] |
李玉伟, 艾池, 张博文, 等.同步压裂对井间裂缝特性的影响[J].断块油气田, 2013, 20(6):779-782. Li Yuwei, Ai Chi, Zhang Bowen, et al.Influence of synchronous volume fracturing on interwell fracture characteristics[J].Fault-Block Oil & Gas Field, 2013, 20(6):779-782. |
| [4] |
赵崇镇.深层砂砾岩水平井组立体缝网压裂优化技术[J].石油钻探技术, 2014, 42(5):95-99. Zhao Chongzhen.3D fracturing network optimization techniques for horizontal wells in sandstone-conglomerate formations[J].Petroleum Drilling Techniques, 2014, 42(5):95-99. |
| [5] |
齐银, 白晓虎, 宋辉, 等.超低渗透油藏水平井压裂优化及应用[J].断块油气田, 2014, 21(4):483-485, 491. Qi Yin, Bai Xiaohu, Song Hui, et al.Fracturing optimization and application of horizontal wells in ultra-low permeability reservoir[J].Fault-Block Oil and Gas Field, 2014, 21(4):483-485, 491. |
| [6] |
陈作, 何青, 王宝峰, 等.大牛地气田长水平段水平井分段压裂优化设计技术[J].石油钻探技术, 2013, 41(6):82-85. Chen Zuo, He Qing, Wang Baofeng, et al.Design optimization of staged fracturing for long lateral horizontal wells in Daniudi Gas Field[J].Petroleum Drilling Techniques, 2013, 41(6):82-85. |
| [7] |
刘力铭, 郭建春, 卢聪, 等.二次加砂压裂技术在樊131区块樊134-1井的应用[J].油气地质与采收率, 2014, 21(1):107-110. Liu Liming, Guo Jianchun, Lu Cong, et al.Application for secondary sand fracturing technology in well Fan 134-1, Fan 131 block[J].Petroleum Geology and Recovery Efficiency, 2014, 21(1):107-110. |
| [8] |
周德华, 焦方正, 贾长贵, 等.JY1HF页岩气水平井大型分段压裂技术[J].石油钻探技术, 2014, 42(1):75-80. Zhou Dehua, Jiao Fangzheng, Jia Changgui, et al.Large-scale multi-stage hydraulic fracturing technology for shale gas horizontal Well JY1HF[J].Petroleum Drilling Techniques, 2014, 42(1):75-80. |
| [9] |
何青, 秦玉英, 姚昌宇, 等.鄂尔多斯盆地南部致密油藏水平井分段压裂技术[J].断块油气田, 2014, 21(6):816-818. He Qing, Qin Yuying, Yao Changyu, et al.Staged fracturing technology of horizontal well for tight oil reservoir in south Ordos Basin[J].Fault-Block Oil and Gas Field, 2014, 21(6):816-818. |
| [10] |
李勇明, 王中武, 郭建春, 等.天然裂缝开启前后的煤层压裂液滤失计算[J].油气井测试, 2006, 15(1):8-9. Li Yongming, Wang Zhongwu, Guo Jianchun, et al.Calculation of fracturing fluid leakoff in coal bed with the reopened natural fractures[J].Well Testing, 2006, 15(1):8-9. |
| [11] | Gale Julia F W.Natural fractures in the Barnett Shale and their important for hydraulic fracture treatment[J].American Association of Petroleum Geologists Bulletin, 2007, 91(4):603-622. |
| [12] |
才博, 丁云宏, 卢拥军, 等.提高改造体积的新裂缝转向压裂技术及其应用[J].油气地质与采收率, 2012, 19(5):108-110. Cai Bo, Ding Yunhong, Lu Yongjun, et al.Study and application of new in-fissure fracturing technique for improving stimulated reservoir volume[J].Petroleum Geology and Recovery Efficiency, 2012, 19(5):108-110. |
| [13] |
彭春耀.层状页岩水力压裂裂缝与岩体弱面的干扰机理研究[J].石油钻探技术, 2014, 42(4):32-36. Peng Chunyao.Mechanism of interaction between hydraulic fractures and weak plane in layered shale[J].Petroleum Drilling Techniques, 2014, 42(4):32-36. |
| [14] |
李扬, 邓金根, 蔚宝华, 等.储/隔层岩石及层间界面性质对压裂缝高的影响[J].石油钻探技术, 2014, 42(6):80-86. Li Yang, Deng Jingen, Yu Baohua, et al.Effects of reservoir rock/barrier and interfacial properties on hydraulic fracture height containment[J].Petroleum Drilling Techniques, 2014, 42(6):80-86. |
| [15] | Blanton T L.Propagation of hydraulically and dynamically induced fractures in naturally fractured reservoirs[R].SPE 15261, 1986. |
| [16] | Warpinski N R, Teufel L W.Influence of geologic discontinuities on hydraulic fracture propagation[J].Journal of Petroleum Technology, 1987, 21(3):209-220. |
| [17] |
李士斌, 秦齐, 张立刚.火山岩气藏体积压裂多裂缝协同效应及控制机理[J].断块油气田, 2014, 21(6):742-745. Li Shibin, Qin Qi, Zhang Ligang.Synergistic effect and control mechanism of volume fracturing fractures for volcano rock gas reservoir[J].Fault-Block Oil & Gas Field, 2014, 21(6):742-745. |
| [18] |
邵尚奇, 田守嶒, 李根生, 等.泥页岩地层水力裂缝延伸方位研究[J].石油钻探技术, 2014, 42(3):27-31. Shao Shangqi, Tian Shouceng, Li Gensheng, et al.Propagating orientation of hydraulic fractures in muddy shale formation[J].Petroleum Drilling Techniques, 2014, 42(3):27-31. |
| [19] | Beugelsdijk L J L, de Pater C J, Sato K.Experimental hydraulic fracture propagation in a multi-fractured medium[R].SPE 59419, 2000. |
| [20] |
金衍, 张旭东, 陈勉.天然裂缝地层中垂直井水力裂缝起裂压力模型研究[J].石油学报, 2005, 26(6):113-118. Jin Yan, Zhang Xudong, Chen Mian.Initiation pressure models for hydraulic fracturing of vertical wells in naturally fractured formation[J].Acta Petrolei Sinica, 2005, 26(6):113-118. |
| [21] |
周健, 陈勉, 金衍, 等.裂缝性储层水力裂缝扩展机理试验研究[J].石油学报, 2007, 28(5):109-113. Zhou Jian, Chen Mian, Jin Yan, et al.Experimental study on propagation mechanism of hydraulic fracture in naturally fractured reservoir[J].Acta Petrolei Sinica, 2007, 28(5):109-113. |
| [22] |
陈勉, 金衍, 张广清.石油工程岩石力学基础[M].北京:石油工业出版社, 2011:38-41. Chen Mian, Jin Yan, Zhang Guangqing.Petroleum engineering rock mechanics basis[M].Beijing:Petroleum Industry Press, 2011:38-41. |



