Simulation Study on the Influences of HTHP on the Results of Microwave Rock Breaking
-
摘要:
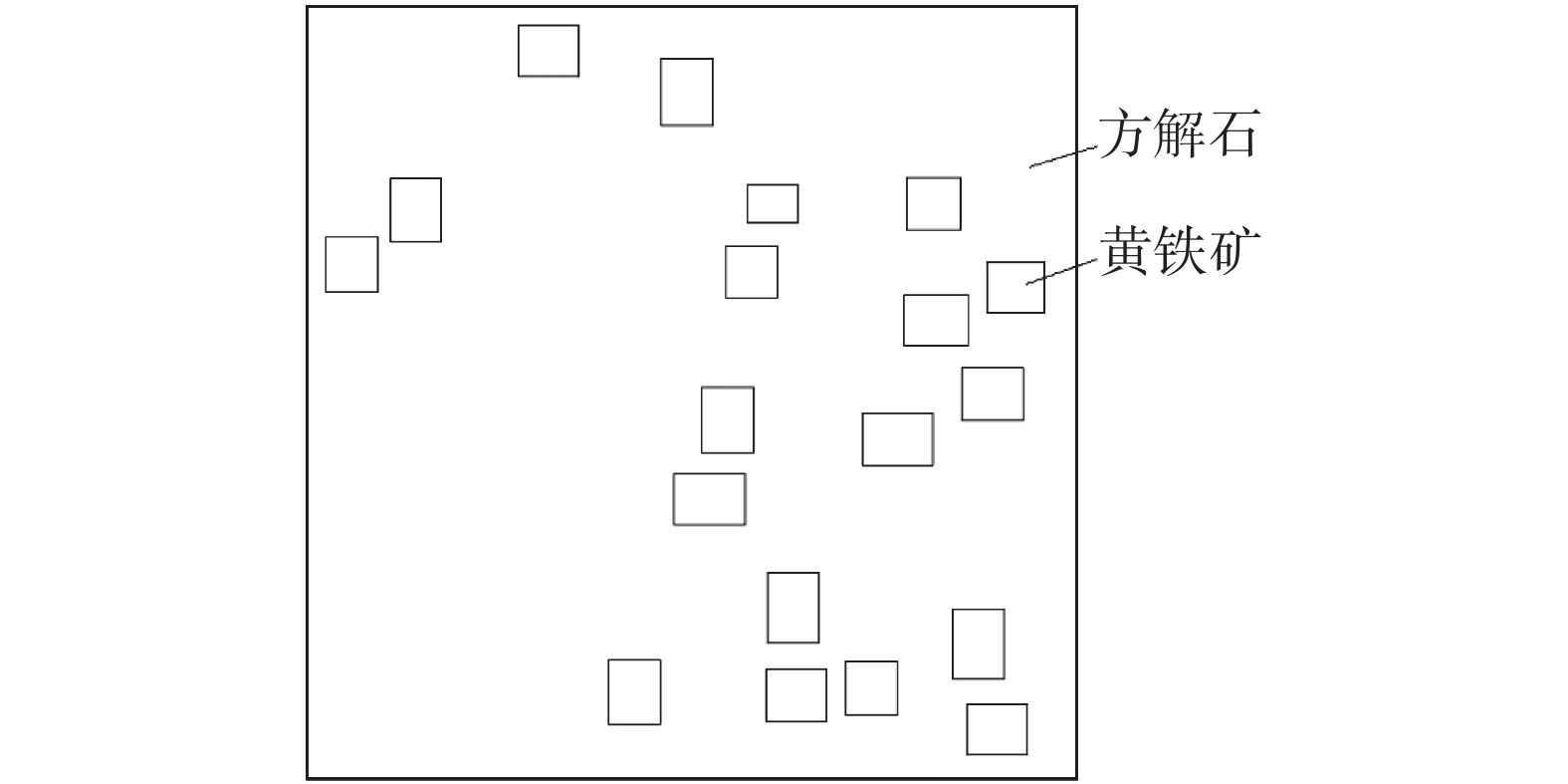
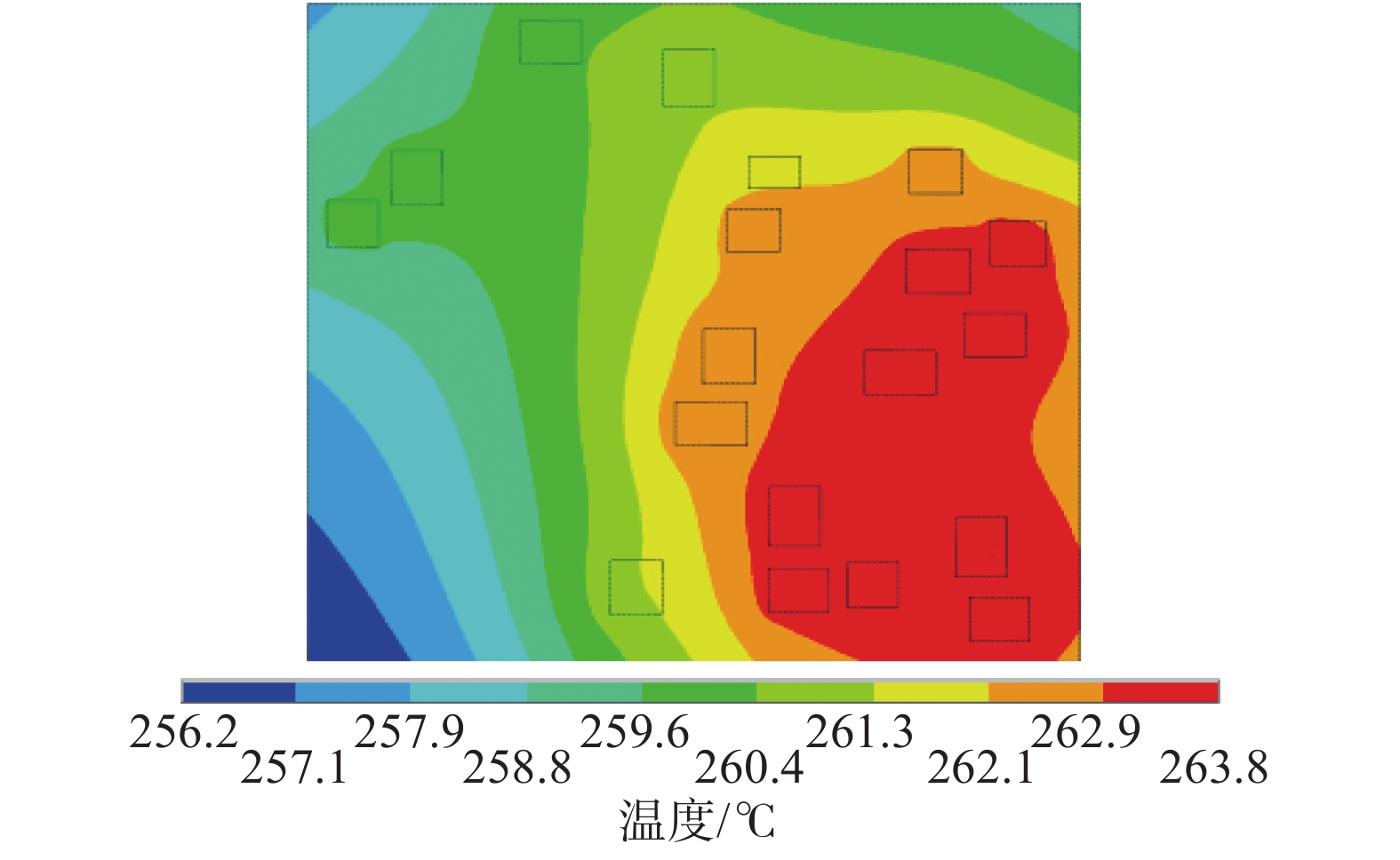
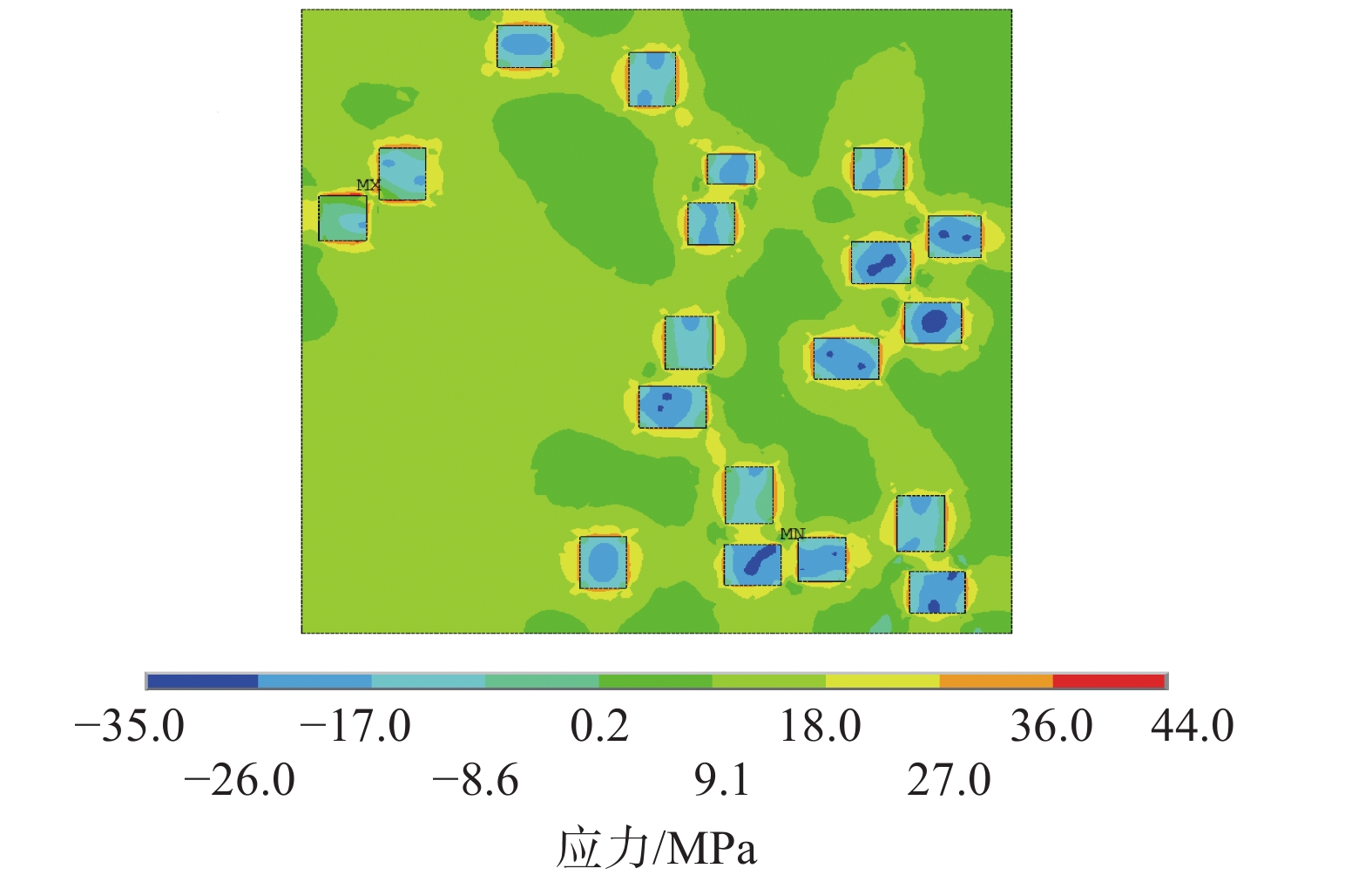
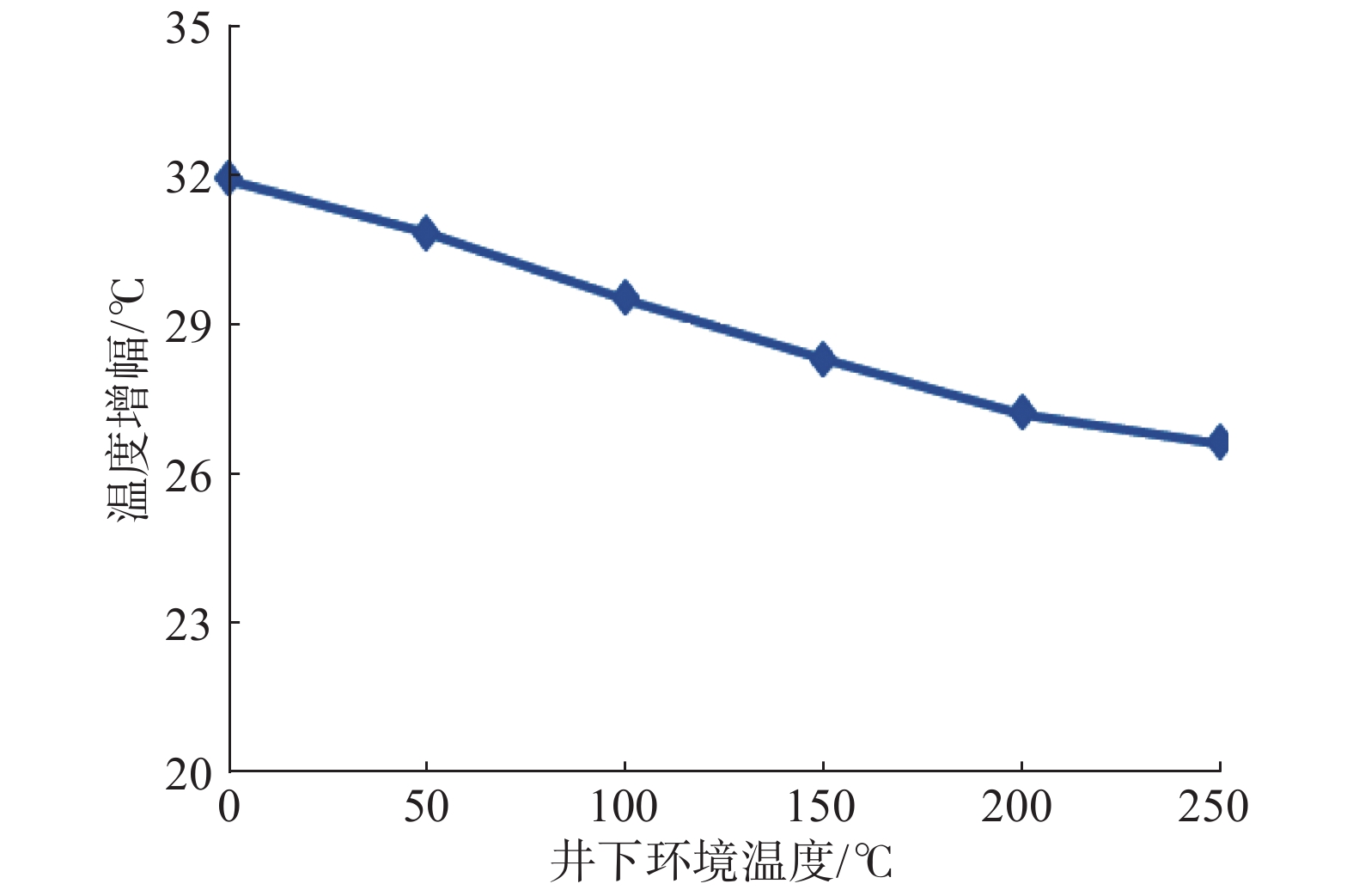
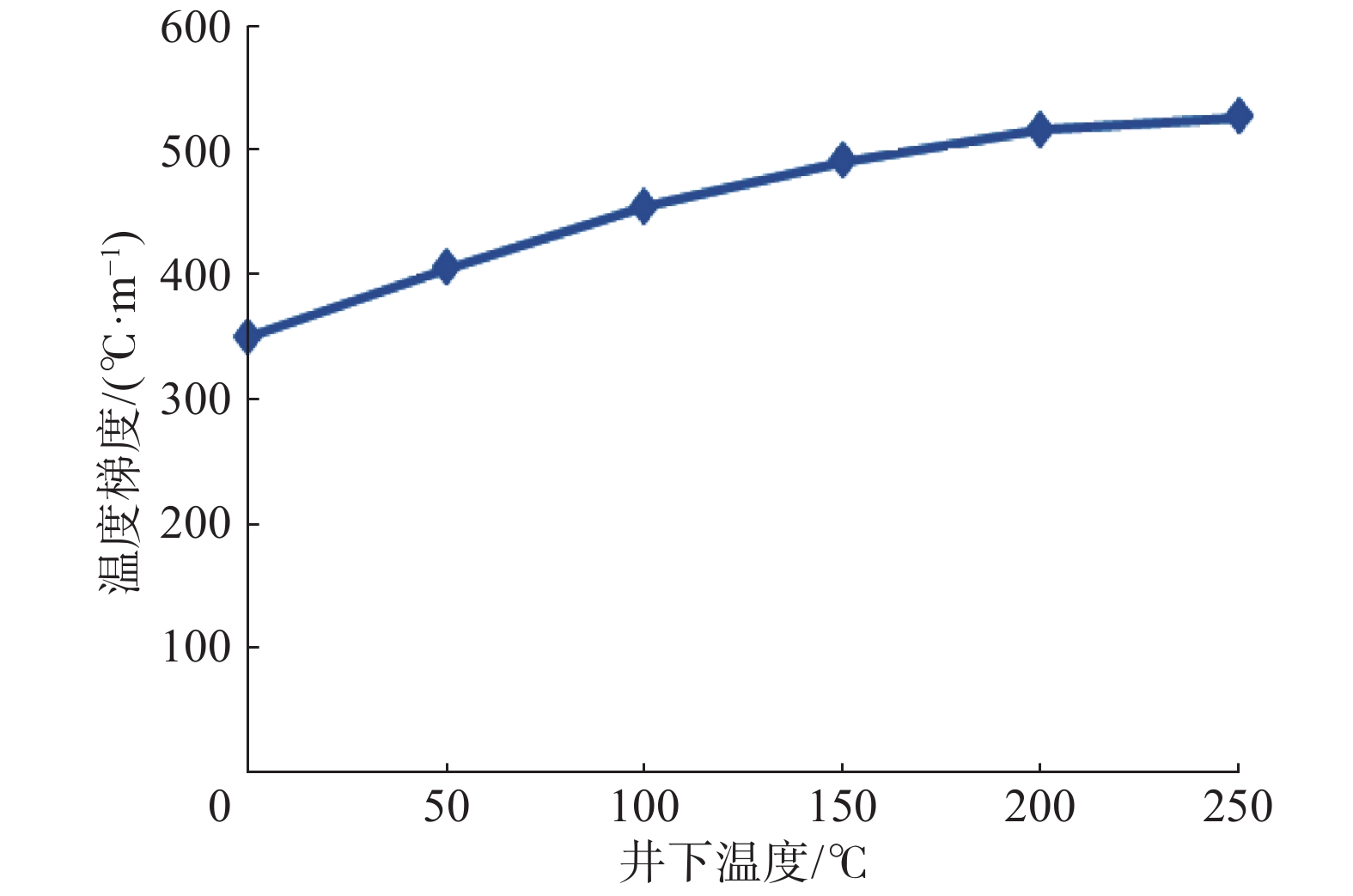
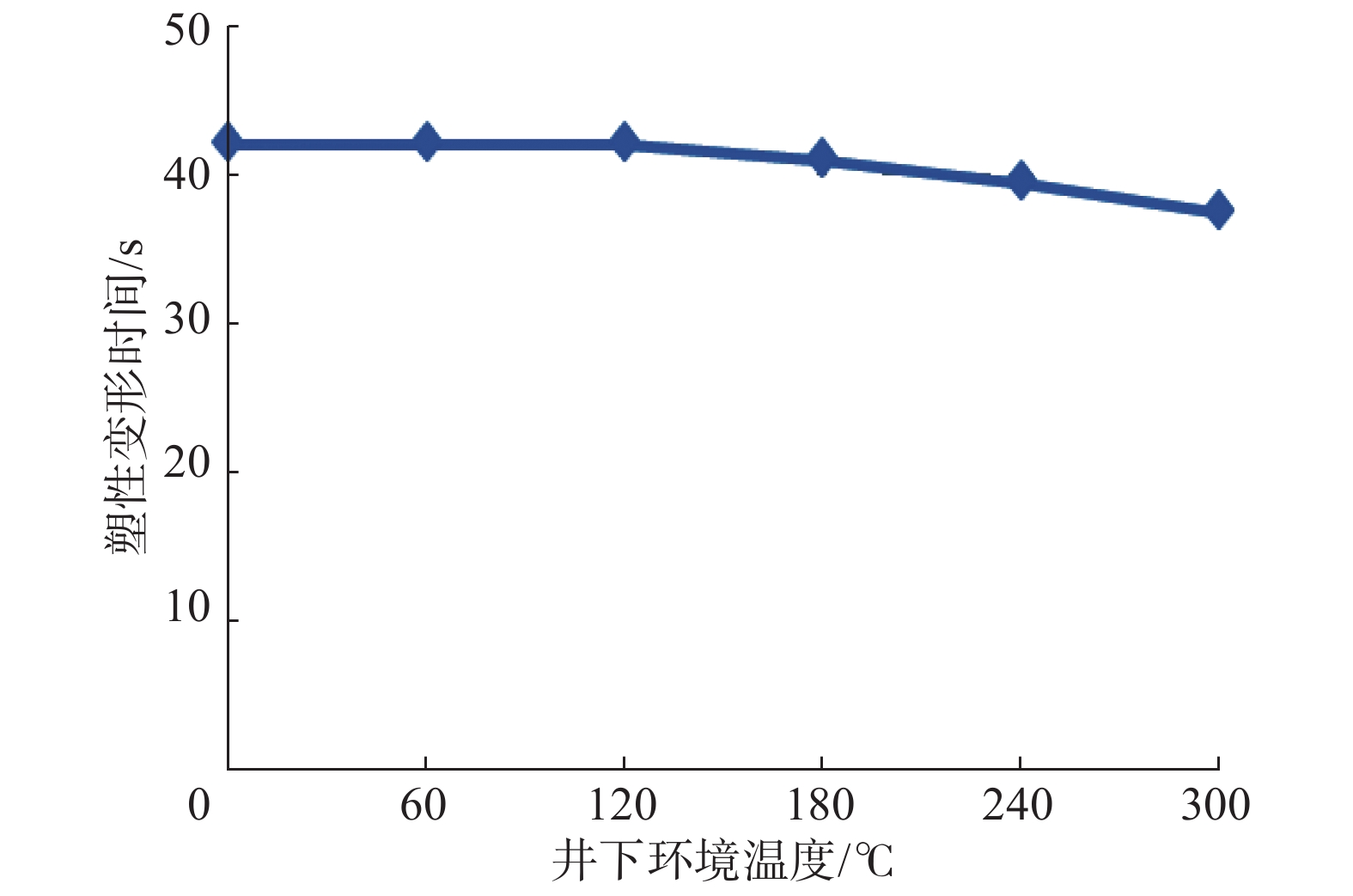
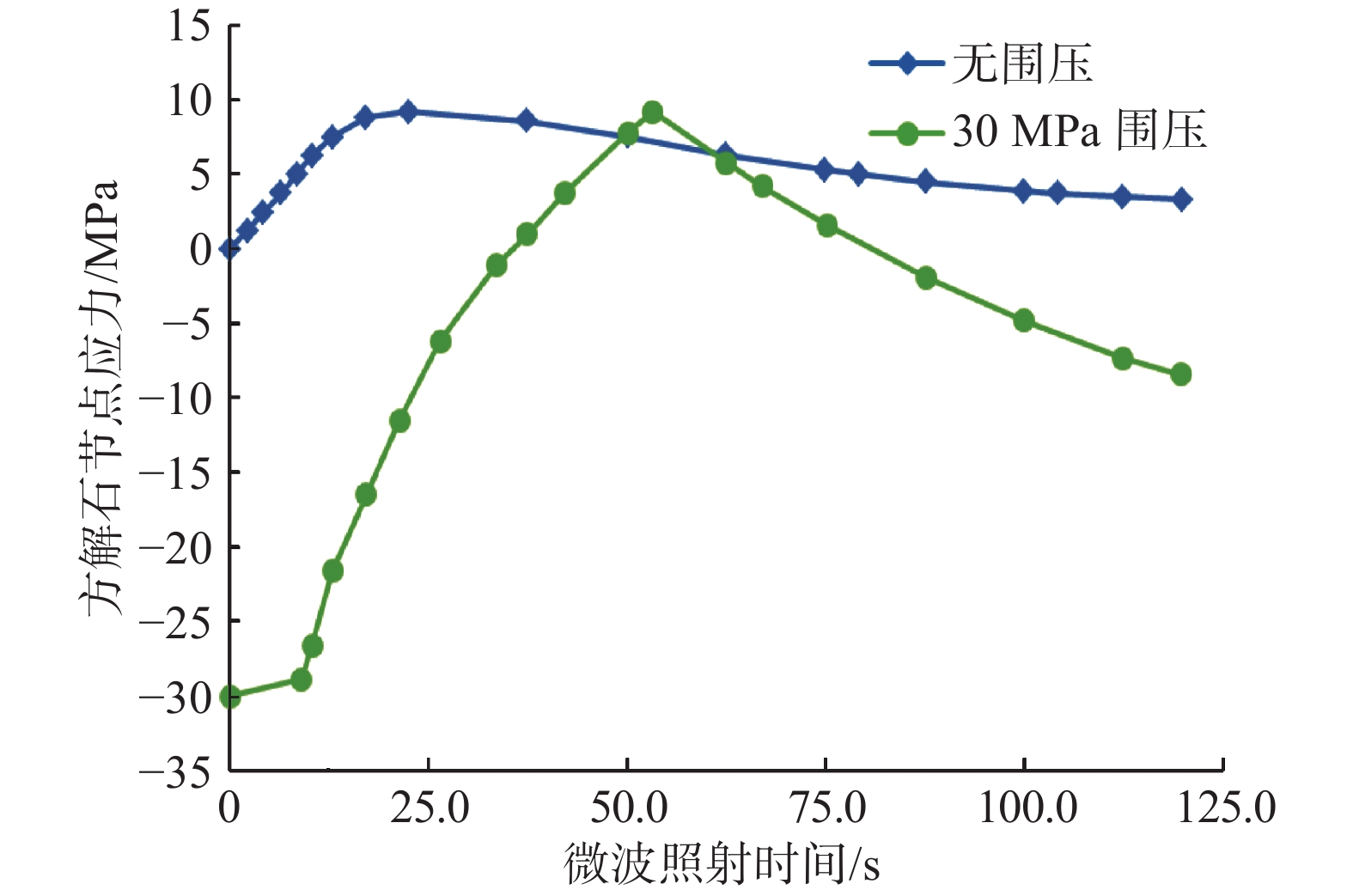
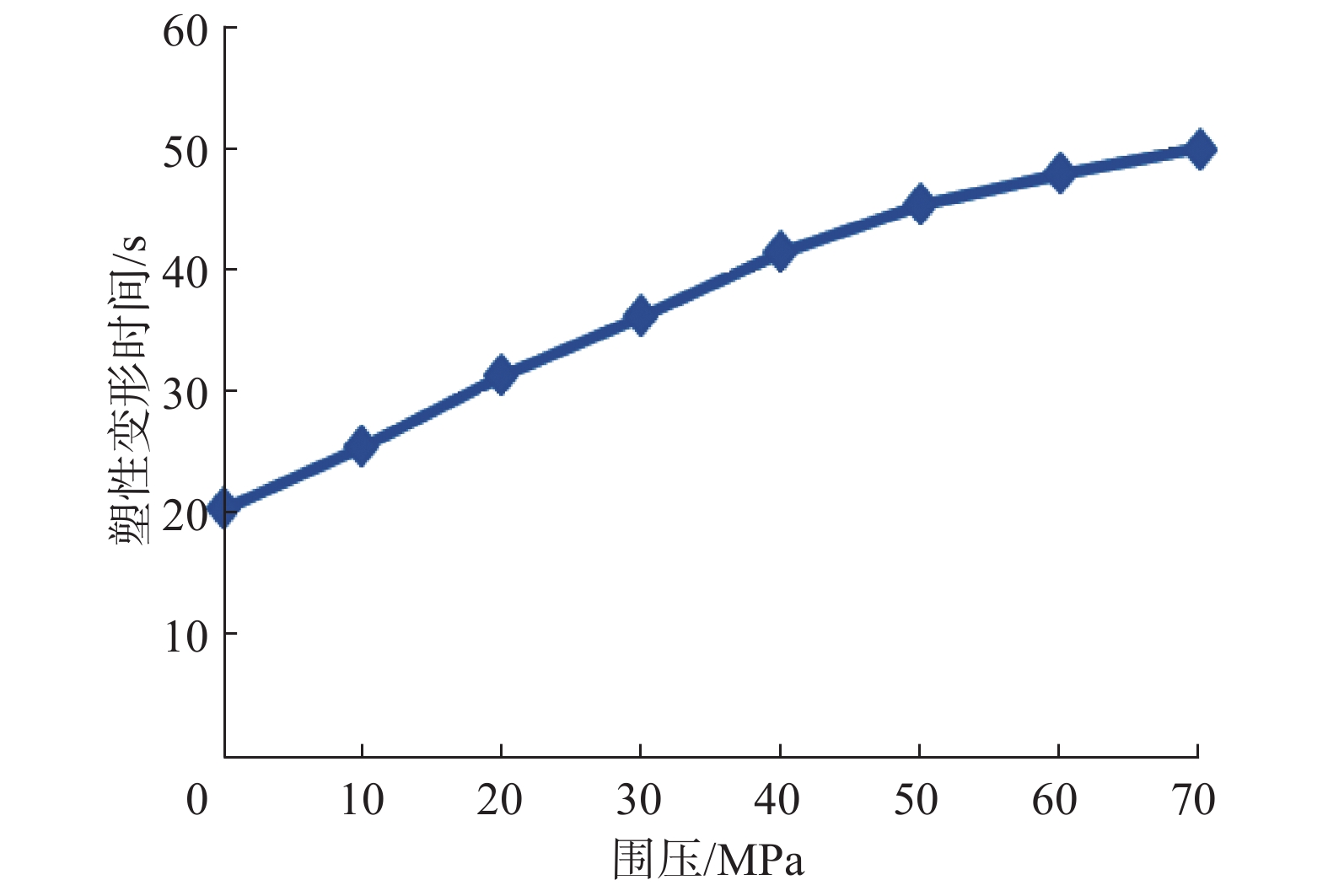
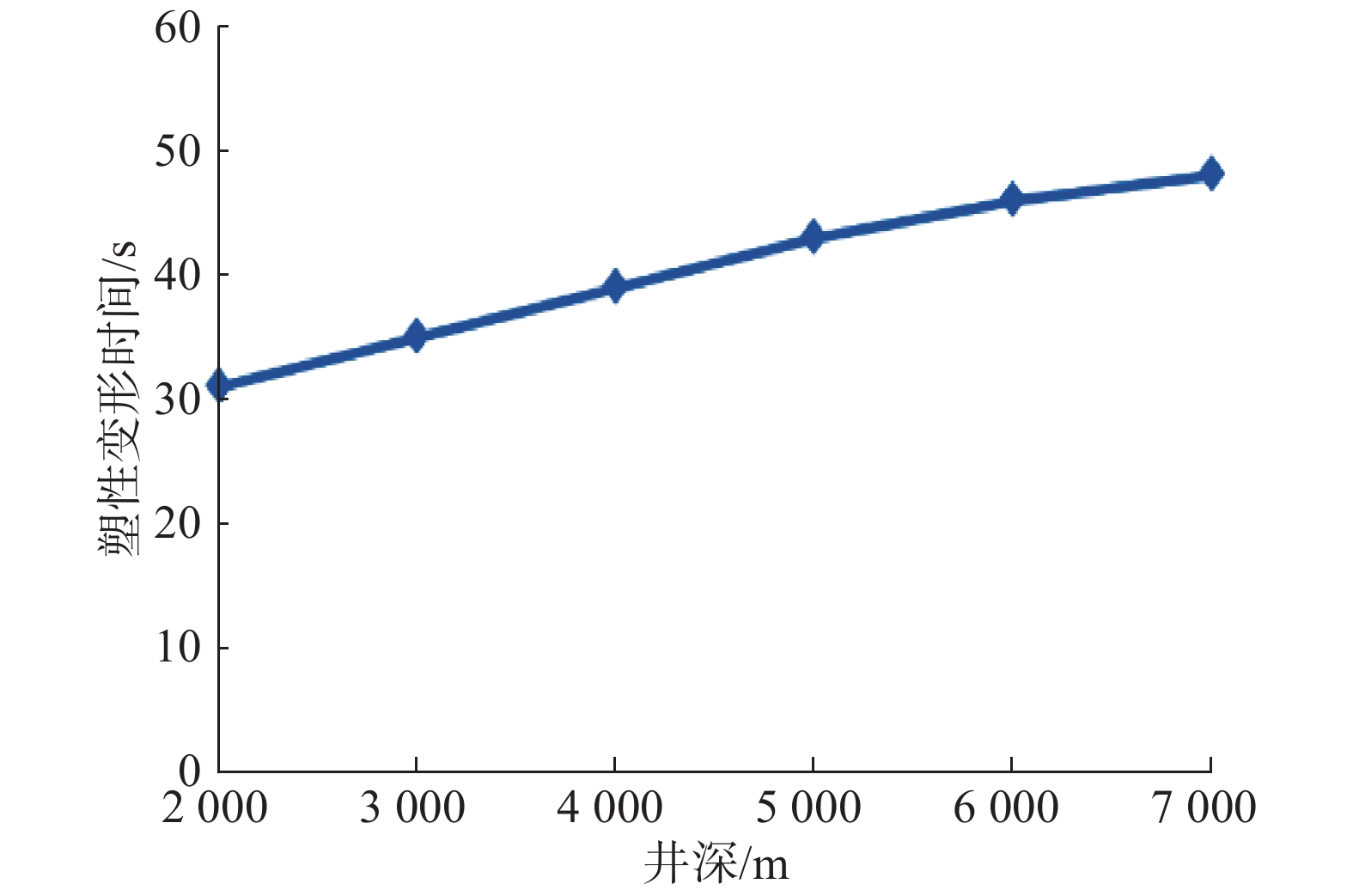
为了将微波破岩技术应用于石油钻井，研究了钻井过程中高温高压对微波破岩效果的影响。根据岩石不同矿物成分的微波吸收特性，建立了某岩石的二维平面模型，模拟分析了温度、围压及二者共同作用对微波破岩效果的影响。研究发现：在微波照射参数相同的情况下，随着井下温度升高，岩石发生塑性变形的时间缩短；随着井下围压增大，岩石塑性变形时间延长；温度和围压共同作用时，围压的影响占主导作用，而温度的影响主要在高温条件下体现。研究结果表明，围压不利于微波破岩，且影响较大；温度对微波破岩有一定促进作用，但只在高温条件下作用明显。因此，应用微波进行破岩时要综合考虑温度和围压变化对破岩效果的影响，及时调整微波参数，使破岩更加经济高效。
Abstract:In order to apply a microwave rock breaking technology in petroleum drilling, the influences of HTHP on the microwave rock breaking result during drilling were studied. According to the microwave absorption characteristics of rock components, a two-dimensional plane model of a rock was established, and the influences of temperature, confining pressure and the combination of both the two on microwave rock breaking result were simulated. The study result found that under the same microwave irradiation parameters, the plastic deformation time of rock shortened with the increase of downhole temperature, and the plastic deformation time of rock increased with the increase of downhole confining pressure. Considering the combined results of both temperature and confining pressure, the influence of confining pressure was dominant, while the effect of temperature mainly exerted under high temperature conditions. The results showed that the confining pressure did not result in microwave rock breaking, and the influence was obvious; temperature had a certain promotion effect on microwave rock breaking, but such an effect was evident only under high temperature conditions. Therefore, when applying microwave in rock breaking, it is necessary to comprehensively consider the influences of temperature and confining pressure on rock breaking results, and to adjust the microwave parameters in time to make the rock breaking more economical and efficient.
-
“电动潜油泵+常规油管+外绑缚铠装电缆”无杆举升技术[1]，是目前国内常用的采油井举升技术之一[2]。然而，进行电动潜油泵采油作业时，油管外捆绑电缆极易造成缆线磨损[1, 3]。为了更高效、安全、低能耗地采油，国内研发了非金属敷缆复合连续油管，将动力电缆、辅热电缆及信号电缆等辅助线缆环形敷设于增强热塑性塑料复合连续管（RTPs）中，不仅可以解决井筒管杆结垢、结蜡、偏磨和外绑电缆故障率高等难题[1, 4]，还能够实现采油系统的智能控制和节能降耗[5]。
在RTPs中嵌入辅助线缆，虽然可以实现智能化采油与控制，但同时也影响敷缆管的力学特性，尤其是敷缆管的结构刚度。此外，敷缆管在安装与服役期间不可避免地承受非工作载荷，尤其在起下及采油过程中会因敷缆管自重而频繁受拉[6–8]，管内缆线也因此发生一定程度变形，若缆线变形量过大，则可能断裂，并使敷缆管失去功能化特性。G. P. Kamp等人[9]介绍了荷兰Airborne公司与英国Shell公司联合研发的智能连续油管，指出当管内导体选用扁铜编织线时导体不易因敷缆管卷曲而损伤。李帅等人[10]通过试验研究了敷缆管起下过程中夹持块对数和加载力对敷缆管最大打滑力的影响。宿振国[11]基于ANSYS软件，研究了敷缆管在内压、拉伸等多种载荷下的受力，并根据蔡−吴失效准则验证了敷缆管结构设计的合理性。丁楠等人[12]基于ABAQUS有限元软件，研究了非金属智能连续管中拉伸层在拉伸、内压及外压载荷下的力学特性。但是，上述研究均未阐明敷缆管中缆线对敷缆管结构层力学响应及敷缆管力学行为的影响。
笔者通过有限元模拟，研究了敷缆复合连续油管在起下及采油过程中承受拉伸载荷时的力学特性及各结构层的力学响应，分析了缆线缠绕角度及缆线分布角度等敷缆工艺参数对敷缆管力学特性的影响，以期为敷缆管的生产制造及安全服役提供依据。
1. 有限元模型的建立
1.1 几何模型
非金属敷缆复合连续油管管体主要由内衬层、敷缆层、玻纤带增强层、芳纶绳抗拉层及外保护层等5部分组成，其结构如图1所示。其中，敷缆层内环形敷设动力缆和加热缆，缆线缠绕角度为10°，动力缆半径为3.0 mm，加热缆半径为2.5 mm；玻纤带增强层及芳纶绳抗拉层的总厚度分别为5.0和2.5 mm，纤维以±50°缠绕；敷缆管内、外径分别为50.0和96.0 mm，其内衬层、外保护层及敷缆层的厚度分别为4.0，3.5和8.0 mm。
![]()
图 1 非金属敷缆复合连续油管结构示意Figure 1. Structure of nonmetallic composite coiled tubing with cable laying非金属敷缆复合连续油管几何模型的构建包括2部分：1）敷缆管管体模型的构建；2）管中缆线的创建，其中，管体采用一体化建模[13]，首先创建1个管道部件（Part1-pipe），然后将管道划分为多层结构；为提高缆线的建模效率与准确性，基于Python语言对有限元软件进行二次开发[14]，通过搭建的缠绕式缆线参数化建模人机交互界面，实现缆线的快速生成，生成的缠绕式缆线装配模型见图2。图2中，红色缆线为加热缆（Part2-heating cable），蓝色缆线为动力缆（Part3-power cable）。将生成的环形缆线嵌入敷缆层中，即可得到非金属敷缆复合连续油管的几何模型，如图3所示。
![]()
图 3 非金属敷缆复合连续油管几何模型Figure 3. Geometric model of nonmetallic composite coiled tubing with cable laying1.2 材料属性
敷缆管内衬层、敷缆层及外保护层均采用高密度聚乙烯（HDPE）制造，而动力缆及加热缆则选用纯铜。有限元模拟时上述2种材料均选用弹塑性本构模型[15]，相关材料的参数见表1。
表 1 HDPE及缆线材料的参数Table 1. Parameters of HDPE and cable materials材料 弹性模量/MPa 泊松比 屈服强度/MPa 抗拉强度/MPa HDPE 850 0.45 25.9 纯铜 108000 0.32 220.0 263.04 玻纤带增强层及芳纶绳抗拉层中不同纤维的力学性能参数由相关生产厂家提供，见表2。上述结构层在宏观上可视为横观各向同性材料[12]，其断裂强度分别为532和360 MPa。在ABAQUS软件中可基于复合材料均质化Halpin-Tsai模型法[16]，采用Composite Layup快捷化建模方式，逐层铺放玻纤带增强层及芳纶绳抗拉层，铺放层数及其纤维层铺放方向（相邻层方向相反）如图4所示（图中，Ply-1表示沿敷缆管径向由内至外铺放的第一层纤维增强层，其他以此类推；下同）。
表 2 不同纤维的力学性能参数Table 2. Mechanical performance parameters of different fibers纤维 断裂强度/
MPa弹性模量/
GPa延伸率，
%密度/
(t·m−3)泊松比 连续无碱玻璃
纤维1 404 72 2.6 2.60 0.22 Kevlar®29纤维 2 900 60 3.6 1.44 0.19 ![]()
图 4 玻纤带增强层及芳纶绳抗拉层铺放方向及层数Figure 4. Laying direction and number of layers of glass fiber tape-reinforced layer and aramid rope tensile layer1.3 边界条件及载荷
首先，在敷缆管两端面中心处设置参考点RP-1和RP-2，并通过Coupling命令将2个端面与参考点耦合。然后，将敷缆管一端的参考点RP-1设置为完全固定约束，在敷缆管另一端的参考点RP-2处通过幅值曲线线性施加80 mm的轴向位移，并约束该点其余方向的自由度。非金属敷缆复合连续油管端部施载情况如图5所示。
![]()
图 5 非金属敷缆复合连续油管端部施载示意Figure 5. Loading on ends of nonmetallic composite coiled tubing with cable laying2. 敷缆管力学特性及其各结构层力学响应分析
2.1 拉伸载荷下敷缆管的力学特性
与RTPs在拉伸载荷下的均匀变形不同[17–18]，敷缆管在拉伸载荷下呈现出非均匀径向收缩（管外保护层径向位移分布如图6所示）。分析认为，这主要是因为敷缆管轴向受拉后，其截面径向收缩，且敷缆层中缆线与增强层中纤维受拉后对截面产生径向压缩作用[19]，但由于管中所敷动力缆及加热缆分布角度各异且直径不同，对截面的径向压缩程度不同，造成敷缆管局部变形不均匀。从图6（b）可以看出，敷缆管1/2横截面处的径向位移呈正弦分布，其最大径向收缩率由式（1）计算得到，约为2.04%。
![]()
图 6 拉伸80 mm后敷缆管外保护层径向位移分布Figure 6. Radial displacement distribution of outer protection layer of pipe with cable laying after stretching 80 mmη=ΔUD×100% (1) 式中：η为敷缆管径向收缩率；ΔU为拉伸载荷下敷缆管径向位移，mm；D为敷缆管外径，mm。
敷缆管轴向伸长量与拉伸载荷的关系曲线如图7所示。从图7可以看出，敷缆管在拉伸载荷下的变形主要经历了弹性阶段（0～1.97 mm）、过渡阶段（1.97～2.76 mm）和屈服阶段（2.76～80.00 mm），这与钢带缠绕增强复合管在拉伸载荷下的力学行为基本一致[20]。敷缆管处于弹性变形阶段时，其拉伸刚度在载荷作用下不发生改变，敷缆管在弹性极限下的轴向承载力约为106.27 kN，根据式（2）可知，敷缆管弹性模量约为10.227 GPa[12]；进一步施加拉伸载荷，敷缆管则进入过渡阶段，其拉伸刚度随轴向位移增大而减小；当敷缆管轴向拉伸位移为2.76 mm时，敷缆管进入屈服阶段，当敷缆管轴向拉伸位移达到80.00 mm时，其轴向承载力为900.60 kN。
![]()
图 7 敷缆管轴向伸长量与拉伸载荷的关系曲线Figure 7. Relationship between axial elongation of pipe with cable laying and tension loadEL=dσdε=4ΔFπ(D22−D21)ΔuL (2) 式中：EL为敷缆管的弹性模量，MPa；ΔF为拉伸载荷，N；Δu为轴向位移，mm；D1为敷缆管内径，mm；D2为敷缆管外径，mm；L为敷缆管长度，mm。
2.2 拉伸载荷下HDPE层的力学响应
在拉伸载荷下，敷缆管中HDPE结构层的应力均因缆线缠绕而呈螺旋式应力分布，各层的最大应力相差不大，但其应力分布形式的差异较大，如图8所示。内衬层敷缆区的应力水平均略低于未敷缆区（见图8（a）），这主要是因为管中环向敷设的缆线在拉伸作用下发生径向收缩，缠绕半径减小[21–22]，内衬层敷缆区受到缆线向内的挤压力[19, 23]，而未敷缆区未受到缆线挤压力的限制，所以其变形相对自由，变形量更大。
![]()
图 8 拉伸位移80 mm时敷缆管中HDPE结构层的应力分布Figure 8. Stress distribution of HDPE structural layer in pipe with cable laying after stretching 80 mm敷缆层加热缆缠绕区的应力水平最高，而动力缆缠绕区的应力水平相对较低，未敷缆区应力水平则处于二者之间，即三者之间关系为加热缆缠绕区应力＞未敷缆区应力＞动力缆缠绕区应力（见图8（b））。这可能是因为加热缆直径略小于动力缆直径且呈单根环向分布，在拉伸载荷下更容易使敷缆层在该处产生应力集中。
外保护层应力分布与上述2个结构层相比，虽然同样呈螺旋式分布，但其敷缆区与未敷缆区应力的分布较均匀，约为26.01 MPa（见图8（c））。
2.3 拉伸载荷下玻纤带增强层的力学响应
拉伸位移为80 mm时，玻纤带增强层中由内至外各层玻纤带沿纤维方向上的最大应力如图9所示。由图9可知，奇数层（缠绕角度50°）玻纤带的最大应力明显高于偶数层（缠绕角度−50°），且随层数增多，最大应力呈线性增大的趋势[24]。其中第7层玻纤带（即Ply-7）的应力最大，约为313.2 MPa（见图10），但低于玻纤带的断裂强度532.0 MPa，表明玻纤带增强层仍具有良好的抗拉性能。
![]()
图 9 拉伸位移80 mm时玻纤带增强层各层的最大应力Figure 9. Maximum stress of each layer of glass fiber tape-reinforced layer after stretching 80 mm![]()
图 10 玻纤带增强层Ply-7沿纤维方向的应力分布Figure 10. Stress distribution of Ply-7 glass fiber tape-reinforced layer along fiber direction2.4 拉伸载荷下芳纶绳抗拉层的力学响应
当敷缆管轴向伸长量为80 mm时，芳纶绳抗拉层沿纤维方向上的最大应力由内至外逐层递减，如图11所示。首层芳纶绳抗拉层（Ply-9）的最大应力约为366.3 MPa，而第二层芳纶绳抗拉层（Ply-10）的最大应力约为337.1 MPa，与首层相比下降了约7.97%。由于芳纶绳抗拉层的断裂强度为360.0 MPa，在拉伸载荷下首层纤维层（Ply-9）最先发生断裂，纤维层断裂则会促使裂纹迅速扩展，进而导致敷缆管整体失效。由此可判定，该结构敷缆管的极限拉伸位移约为80 mm。
![]()
图 11 拉伸位移为80 mm时芳纶绳抗拉层沿纤维方向的应力分布Figure 11. Stress distribution of aramid rope tensile layer along fiber direction after stretching 80 mm2.5 拉伸载荷下缆线的力学响应
管内的辅助线缆是敷缆管实现智能化采油与控制的关键。然而，在拉伸载荷作用下，管中缆线会与敷缆管一起变形，当缆线变形量过大时，不仅会降低信号传输效率，还会影响敷缆管的力学特性。因此，明确管中缆线的力学行为尤其重要。
拉伸位移与管内缆线应力变化趋势如图12所示。从图12可以看出，在拉伸载荷下，缆线整体变形较均匀，当敷缆管轴向拉伸位移为2.65 mm时，管中缆线开始屈服，对比图7可知，敷缆管在拉伸载荷下的变形历程较大程度依赖于管中缆线的变形状态。当缆线屈服以后，拉伸载荷对其应力的影响减弱，继续增加拉伸位移至敷缆管发生失效时，管内缆线的最大应力约为242.379 MPa，全部发生了塑性变形，但塑性变形量较小，最大等效塑性应变仅为8.516%。敷缆管失效时缆线的最大应力低于其抗拉强度263.04 MPa，缆线并未断裂且处于小塑性均匀变形状态，因此在拉伸载荷下敷缆管变形不会影响其中动力缆和加热缆的正常工作。
![]()
图 12 拉伸位移80 mm时缆线应力的变化趋势Figure 12. Trend of cable stress variation after stretching 80 mm3. 敷缆工艺参数对敷缆管力学特性的影响
3.1 缆线缠绕角度
以构建的有限元模型为基础，采用单因素法，研究了拉伸位移5 mm时缆线缠绕角度对敷缆管力学特性的影响，如图13所示。
![]()
图 13 敷缆管中缆线缠绕角度对敷缆管力学性能的影响Figure 13. Influence of cable winding angle on mechanical properties of pipe with cable laying从图13可以看出，拉伸位移为5mm时RTPs始终处于弹性变形状态，而管内植入缆线后，敷缆管力学特性发生了较大改变。管内缆线缠绕角度为10°和20°、拉伸为5 mm时，敷缆管均经历了弹性变形阶段（0A1、0A2）、过渡阶段（A1B1、A2B2）及屈服阶段（B1C1、B2C2）；缆线缠绕角度继续增至30°、40°时，在相同拉伸位移下，敷缆管整体仍保持弹性变形阶段。由此可知，缆线缠绕角度对敷缆管在拉伸载荷下的变形历程具有重要影响，缆线缠绕角度越大，敷缆管在拉伸载荷下更易处于弹性变形阶段；若管中缆线以小角度缠绕，敷缆管则会提前进入过渡阶段，进而更早发生屈服，但小角度缠绕却能够显著提高敷缆管的轴向承载能力。缆线缠绕角度10°敷缆管轴向伸长5 mm时所受的拉伸载荷约为167.34 kN，与缠绕角度40°时所受的拉伸载荷131.43 kN相比，增加了约27.3%，相比RTPs其抗拉性能提升了约165.5%。
此外，相比RTPs，管内敷设缆线会提高敷缆管弹性模量，且随着缆线缠绕角度增大，敷缆管弹性模量逐渐降低[25]，当缆线缠绕角度从10°增至40°时，由式（2）可计算得到敷缆管弹性模量约降低了49.5%。这主要是因为，增大缆线缠绕角度，会增加敷缆管单位轴向长度内缆线缠绕的圈数，而螺旋式缆线的弹性变形量与圈数呈正比例关系[17, 20, 26]，因此，当缆线以大角度缠绕相同敷缆管长度时，更易发生弹性变形，使敷缆管整体弹性模量减小。
不同缆线缠绕角度下各结构层的最大应力如图14所示。由图14可知，在拉伸载荷下玻纤带增强层及芳纶绳抗拉层为主要的承力构件，这2个结构层沿纤维方向上的最大应力随着缆线缠绕角度增大均呈现出先增大后减小的趋势。然而，当缆线缠绕角度逐渐增大时，内衬层和敷缆层的最大应力大致呈增大趋势；而外保护层则对缆线缠绕角度的变化并不敏感，其最大应力随缆线缠绕角度的变化在6 MPa上下轻微波动。
![]()
图 14 缆线缠绕角度对敷缆管各结构层最大应力的影响Figure 14. Influence of cable winding angle on maximum stress of each structural layer of pipe with cable laying3.2 缆线分布角度
缆线分布角度对敷缆管弹性模量及轴向承载性能的影响如图15所示。
![]()
图 15 动力缆分布角度对敷缆管力学性能的影响Figure 15. Influence of distribution angle of power cable on mechanical properties of pipe with cable laying由图15可知，增大缆线分布角度，敷缆管的弹性模量和其轴向承载性能均略微降低，缆线分布角度无法改变敷缆管在拉伸载荷下的变形历程。与缆线缠绕角度的影响类似，缆线分布角度对敷缆管内衬层、敷缆层及外保护层最大应力的影响不大，但玻纤带增强层和芳纶绳抗拉层沿纤维方向上的最大应力却随缆线分布角度增大呈先增大后减小的趋势，且均在缆线分布角度为55°时达到最大，该角度下玻纤带增强层的最大应力为52.12 MPa，芳纶绳抗拉层的最大应力约为41.14 MPa（见图16）。
![]()
图 16 缆线分布角度对敷缆管各结构层最大应力的影响Figure 16. Influence of cable distribution angle on maximum stress of each structural layer of pipe with cable laying4. 结 论
1） 敷缆管在拉伸载荷下其横截面出现了非均匀收缩，最大径向收缩率约为2.04%。敷缆管拉伸至失效历经弹性变形、过渡和屈服等3个阶段。
2） 拉伸载荷下，敷缆管中所有结构层均因缆线缠绕而呈现出螺旋式应力分布。其中，玻纤带增强层及芳纶绳抗拉层为该载荷下的主要承力结构层，且芳纶绳抗拉层是敷缆管最先断裂的结构层。
3） 当敷缆管拉伸至失效时，管中缆线应力并未达到材料的抗拉强度，缆线最大等效塑性应变仅为8.516%，处于小塑性均匀变形状态，所以在拉伸载荷下，缆线的微量变形不影响其信号的传输效率。
4） 管内玻纤带增强层和芳纶绳抗拉层沿纤维方向上的最大应力，均随缆线缠绕角度和分布角度增大呈现出先增大后减小的趋势。但是，缆线分布角度对敷缆管弹性模量及其轴向承载能力的影响极小，而减小缆线缠绕角度却可以显著提高敷缆管的弹性模量及其轴向承载能力，但也会导致敷缆管提前进入过渡阶段，继而发生屈服。因此，在生产制造该类敷缆管时应着重考虑管内缆线的缠绕角度。
-
![]()
图 5 微波照射下模型的塑性变形
Figure 5. Plastic deformation of the model under microwave irradiation
![]()
图 6 不同环境温度下方解石某节点的温度增幅
Figure 6. Temperature amplification of a node in calcite under different ambient temperatures
![]()
图 7 不同环境温度下方解石某节点的温度梯度极值
Figure 7. Temperature gradient extremum of a node in calcite under different ambient temperatures
![]()
图 8 不同环境温度下方解石某节点的塑性变形时间
Figure 8. Plastic deformation times of a node in calcite under different ambient temperatures
![]()
图 9 施加围压前后方解石某节点的应力对比
Figure 9. Comparison on the force of a node in calcite before and after confining pressure
![]()
图 10 不同围压下方解石某节点的塑性变形时间
Figure 10. Plastic deformation times of a node in calcite under different confining pressures
![]()
图 11 不同温度和围压作用下方解石某节点的塑性变形时间
Figure 11. Plastic deformation times of a node in calcite under different temperature and confining pressure
表 1 岩石各成分的热膨胀系数
Table 1 Thermal expansion coefficients of various rock components
温度/℃ 热膨胀系数/℃–1 方解石 黄铁矿 100 1.31×10–5 2.73×10–5 200 1.58×10–5 2.93×10–5 300 2.01×10–5 3.39×10–5 400 2.40×10–5 
下载: 导出CSV
表 2 岩石各成分在不同温度下的热传导系数及比热
Table 2 Thermal conductivity and specific heat of various rock components at different temperatures
岩石
成分热传导系数/（W·m–1·℃–1） 比热/（J·kg–1·℃–1） 25 ℃ 100 ℃ 227 ℃ 25 ℃ 227 ℃ 727 ℃ 方解石 4.02 3.01 2.55 819 1 051 1 238 黄铁矿 37.90 20.50 17.00 517 600 684
下载: 导出CSV
表 3 岩石各成分的力学参数
Table 3 Mechanical parameters of various rock component
岩石
成分密度/
（kg·m–3）弹性模量/
GPa泊松比 摩擦角/
（°）黏聚力/
MPa方解石 2 680 797 0.32 54 25 黄铁矿 5 018 292 0.16 54 25
下载: 导出CSV
-
[1] 赵志国, 白彬珍, 何世明, 等. 顺北油田超深井优快钻井技术[J]. 石油钻探技术, 2017, 45(6): 8–13. ZHAO Zhiguo, BAI Binzhen, HE Shiming, et al. Optimization of fast drilling technology for ultra-deep wells in the Shunbei Oilfield[J]. Petroleum Drilling Techniques, 2017, 45(6): 8–13.
[2] 张强. 岩石破碎技术发展趋势[J]. 有色矿山, 1996(6): 20–22. ZHANG Qiang. Rock-breaking technology trends[J]. China Mine Engineering, 1996(6): 20–22.
[3] 鲍挺, 黄宁. 岩石破碎技术研究与发展前景[J]. 安徽建筑, 2010(6): 110, 116. BAO Ting, HUANG Ning. The research and development prospects of rock-breaking technology[J]. Anhui Architecture, 2010(6): 110, 116.
[4] VIKTOROV S D, KUZNETSO A P. Explosive breaking of rock: a retrospective and a possible alternative[J]. Journal of Mining Science, 1998, 34(1): 43–49. doi: 10.1007/BF02765524
[5] 李文成, 杜雪鹏. 微波辅助破岩新技术在非煤矿的应用[J]. 铜业工程, 2010(4): 1–4. doi: 10.3969/j.issn.1009-3842.2010.04.001 LI Wencheng, DU Xuepeng. Application of microwave-assisted rock breaking in metal mines[J]. Coffer Engineering, 2010(4): 1–4. doi: 10.3969/j.issn.1009-3842.2010.04.001
[6] 郭先敏. 毫米波钻井技术[J]. 石油钻探技术, 2014, 42(3): 55–60. GUO Xianmin. Millimeter wave drilling technology[J]. Petroleum Drilling Techniques, 2014, 42(3): 55–60.
[7] KINGMAN S W. Recent developments in microwave processing of minerals[J]. International Materials Reviews, 2006, 51(1): 1–12. doi: 10.1179/174328006X79472
[8] LOVÁS M, KOVÁČOVÁ M, DIMITRAKIS G, et al. Modeling of microwave heating of andesite and minerals[J]. International Journal of Heat and Mass Transfer, 2010, 53(17/18): 3387–3393.
[9] HASSANI F, NEKOOVAGHT P M, GHARIB N. The influence of microwave irradiation on rocks for microwave-assisted underground excavation[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2016, 8(1): 1–15. doi: 10.1016/j.jrmge.2015.10.004
[10] AZAR M, KESHAVAN M, COOPER I M. Energy-emitting bits and cutting elements: WO2017/151353[P/OL]. 2017-09-08[2018-08-12]. https://patentscope.wipo.int/search/zh/detail.jsf?docId=WO2017151353&redirectedID=true
[11] 戴俊, 孟振, 吴丙权. 微波照射对岩石强度的影响研究[J]. 有色金属(选矿部分), 2014(3): 54–57. doi: 10.3969/j.issn.1671-9492.2014.03.014 DAI Jun, MENG Zhen, WU Bingquan. Study on impact of rock strength by microwave irradiation[J]. Monferrous Metals(Mineral Processing Section), 2014(3): 54–57. doi: 10.3969/j.issn.1671-9492.2014.03.014
[12] 卢高明, 李元辉, HASSANI Ferri, et al. 微波辅助机械破岩试验和理论研究进展[J]. 岩土工程学报, 2016, 38(8): 1497–1506. LU Gaoming, LI Yuanhui, HASSANI F, et al. Review of theoretical and experimental studies on mechanical rock fragmentation using microwave-assisted approach[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1497–1506.
[13] 戴俊, 秦立科. 微波照射下岩石损伤细观模拟分析[J]. 西安科技大学学报, 2014, 34(6): 652–655. DAI Jun, QIN Like. Meso-simulation of rock damage under microwave irradiation[J]. Journal of Xi’an University of Science and Technology, 2014, 34(6): 652–655.
[14] 黄孟阳, 彭金辉, 雷鹰, 等. 微波场中钛精矿的温升行为及吸波特性[J]. 四川大学学报(工程科学版), 2007, 39(2): 111–115. doi: 10.3969/j.issn.1009-3087.2007.02.021 HUANG Mengyang, PENG Jinhui, LEI Ying, et al. The temperature rise behavior and microwave-absorbing characteristics of ilmenite concentrate in microwave field[J]. Journal of Sichuan University (Engineering Science Edition), 2007, 39(2): 111–115. doi: 10.3969/j.issn.1009-3087.2007.02.021
[15] 陈超, 刘建. 数值分析方法在微波辅助破岩中的应用[J]. 华北理工大学学报(自然科学版), 2017, 39(4): 28–33. doi: 10.3969/j.issn.2095-2716.2017.04.005 CHEN Chao, LIU Jian. Application of numerical analysis method in microwave assisted rock breaking[J]. Journal of North China University of Science and Technology(Natural Science Edition), 2017, 39(4): 28–33. doi: 10.3969/j.issn.2095-2716.2017.04.005
[16] 唐阳, 徐国宾, 孙丽莹, 等. 不同间断比尺下微波诱发岩石损伤的离散元模拟研究[J]. 水力发电学报, 2016, 35(7): 15–22. TANG Yang, XU Guobin, SUN Liying, et al. Discrete element modeling of microwave-induced rock damage at different discontinuity scales[J]. Journal of Hydroelectric Engineering, 2016, 35(7): 15–22.
[17] 杨晓庆, 黄卡玛, 黄镇钢, 等. 微波加热模拟中的关键问题讨论[J]. 压电与声光, 2008, 30(2): 105–107. YANG Xiaoqing, HUANG Kama, HUANG Zhengang, et al. Study on the key problems of numeric simulation of microwave heating[J]. Piezoelectectrics & Acoustooptics, 2008, 30(2): 105–107.
[18] 秦立科, 戴俊. 微波照射下矿物颗粒温度分布及影响因素分析[J]. 矿冶工程, 2015, 35(3): 96–98. doi: 10.3969/j.issn.0253-6099.2015.03.026 QIN Like, DAI Jun. Temperature distribution and influential factors for ore particles under microwave irradiation[J]. Mining and Metallurgical Engineering, 2015, 35(3): 96–98. doi: 10.3969/j.issn.0253-6099.2015.03.026
计量
- 文章访问数: 12160
- HTML全文浏览量: 6229
- PDF下载量: 80
