在含超高阻盐膏层钻井时, 由于采用了随钻防漏堵漏技术, 脉冲随钻测量仪(MWD)无法正常工作[1-4], 而地层电阻率过高会导致电磁信号急速衰减, 常规电磁MWD发出的信号无法通过盐膏层[5-8], 定向作业面临缺乏随钻测量手段的难题[9]。井下电磁中继器可以随钻实时对电磁MWD发出的信号进行无线转发, 从而增强地面接收到的电磁信号强度, 使电磁MWD传输距离满足需求。因此, 准确分析超高阻盐膏层中电磁中继信号的衰减特性和预判电磁中继器的安装位置, 能够确保电磁MWD信号在盐膏层中连续传输, 为钻进盐膏层提供有效的随钻测量手段。电磁中继技术作为一项全新的技术, 目前国内仅有中国石化石油工程技术研究院研制出了成熟产品[10];而在超高阻盐膏层电磁中继传输特性分析和电磁中继器安装位置预测方面, 目前尚无相关研究工作的报道。
笔者针对超高阻盐膏层随钻中继转发时井下地层环境复杂[11]、存在多个电磁发射器等难点, 采用同时细化空间和阶次的自适应HP有限元算法, 对含有超高阻盐膏层施工井的电磁信号的传输和中继转发过程进行了模拟, 迭代求解得到了信号传输时地层模型中的电场分布情况, 最终获得了施工井中不同频率载波条件下电磁信号衰减速度和传输距离之间的关系, 并以此为依据预测了电磁中继器的安装位置。现场试验证明, 该算法具有较高的预测精度, 能够提高电磁MWD的现场应用效果。
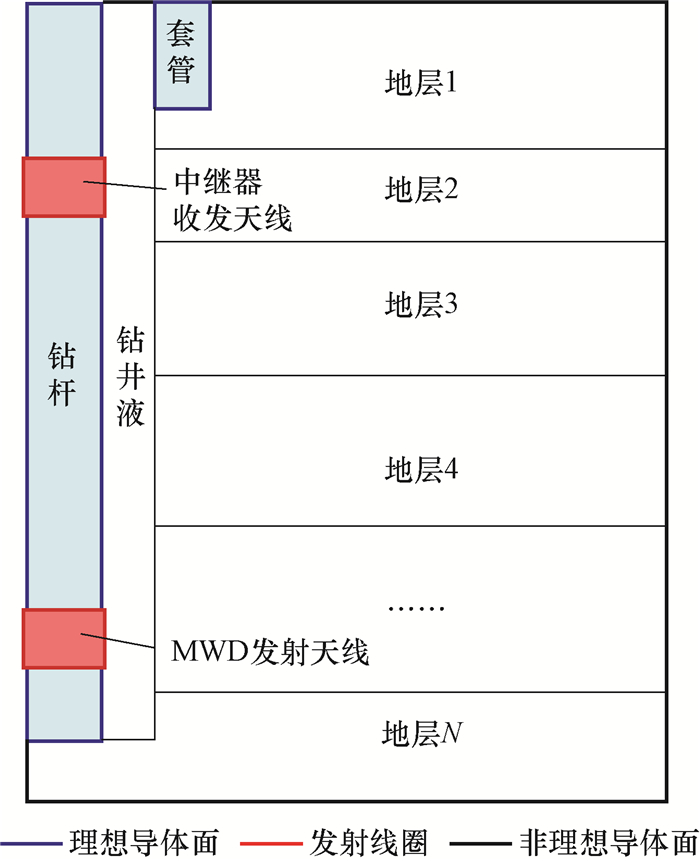
1 中继传输模型的建立及求解 1.1 有限元模型的建立井下电磁中继传输特性求解的基础是准确建立有限元模型, 首先按实际的地层情况构建不均匀地层条件下的有限元几何模型(见图 1)。模型应按照实际钻井环境建立, 电磁MWD和电磁中继器的天线结构与实际使用的钻杆耦合式天线一致, 模型由水平地层构成, 地层数量、各地层电阻率取值、钻杆和钻井液等介质各参数值均根据实钻井的工程、地质参数设置。
|
| 图 1 井下电磁中继转发初始几何模型 Fig.1 Downhole initial mesh model of electromagnetic relay while drilling |
由于电磁MWD和电磁中继器使用的都是几到几十赫兹的超低频信号, 该信号是由施加在钻杆耦合天线绝缘段两极的交变电流激励感生的, 其本质是对井下时谐电场强度分布情况的求解, 因此对时谐麦克斯韦方程进行化简并积分, 可以得到电磁传输波动方程:
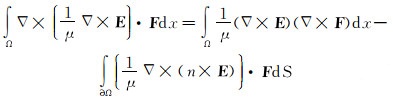
|
(1) |
式中:Ω为模型求解域;μ为传输信道(例如钻杆、地层等介质)的磁导率, H/m;E为所求电场强度, V/m;F为取梯度后的Lobatto试函数。
根据求解域中存在介质的种类, 求解域中主要包含3种边界条件:理想导体面、地层各分层、钻井液等非理想导体面和发射天线。理想导体是指电磁传输过程中不会发生损耗的介质, 例如钻杆等, 其表面边界条件ΓP为:

|
(2) |
式中:n为边界的外法向单位矢量。
地层各分层、钻井液等非理想导体, 2个介质的分界面处为阻抗边界条件ΓI为:
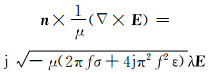
|
(3) |
式中:j为虚数单位;f为电磁信号载波频率, Hz;σ为传输介质的电导率, S/m;ε为传输介质的相对介电常数;λ为非理想导体的阻抗, Ω。
发射天线作为单独的激励介质其边界条件ΓA为:
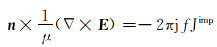
|
(4) |
式中:Jimp是施加在发射天线两极的激励电流密度, A/m2。
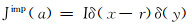
|
(5) |
式中:r为天线半径, m;I为天线两极施加的激励电流强度, A;δ为狄拉克函数, 其数学表达式为
式(1)中加入上述边界条件进行约束后, 可获得电场强度的有限元求解变分方程:

|
(6) |
式中:ET为电场强度E边界方向上的切向分量, V/m;FT为试函数F边界方向上的切向分量。
根据求解出的电场强度, 即可计算出地面接收电极接收到的电压信号强度:
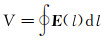
|
(7) |
式中:V为地面接收电极上接收到的信号电压, V;l为接收电极半径, m。
同理, 可获得电磁中继器的有限元数学模型。根据电磁MWD和电磁中继器的工作原理, 任意时刻内有且只有一种仪器的天线在发射电磁信号, 因此模型中电磁MWD和电磁中继器的感生电场求解实际是2个互不干涉的过程。
1.2 模型求解对有限元模型进行求解时, 首先需要针对模型构建自适应HP有限元计算方法细化策略, 即根据地层有限元模型的实际情况和要求的求解精度自动选择下一步的细化和计算对象, 其他区域维持不变。通过对模型各网格的误差分析, 将常规的全局计算缩小为针对局部单元网格的计算, 电场变化比较平缓的区域, 选择使用H细化方式缩小网格尺寸;电场变化剧烈的区域, 使用P细化增加网格形函数阶次, 从而降低计算复杂度和缩短计算时间。与传输线矩阵、常规有限元等全域计算的算法[12-18]相比, 自适应HP有限元算法的收敛速度和求解精度更高, 具体细化策略如下:
1) 设求解的最大误差容许范围Δer>0, 将初始求解域ΩH, P中所有网格进行H细化和多项式阶次P加1, 此时求解域Ωref变为:
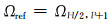
|
(8) |
求解可得电场强度的参考解Eref。
2) 初始网格中选择网格K细化成4个子单元Ki(1≤i≤4), 此时子单元计算误差eri为:
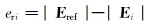
|
(9) |
式中:Ei为每个子单元求解得到的电场强度E的近似解, V/m。
则细化后网格的全局误差er为:
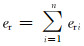
|
(10) |
3) 如er≤Δer, 则计算完成;否则, 将所有细化单元按误差递减顺序加入序列L中。
4) 在序列L中选择误差最大的单元作为下一次计算的初始网格, 继续从步骤2)开始计算, 直至er≤Δer, 此时各子单元求解得到的电场强度即为子单元所在地层位置处电场强度的最终解。
求解实钻井所建模型时, 首先根据实钻井的钻井工程设计方案和地质设计方案对所建模型中井深、井径、钻井液介质和地层电阻率等参数进行设置, 在已建几何模型中分别输入每个地层对应的电阻和深度;然后, 电磁MWD发射天线从模型左上角开始下移来模拟实际钻进过程, 每下移一次使用自适应HP有限元细化策略求解当前地面接收电极所在子单元的电压强度, 并代入式(7)计算出电极接收到的地面信号强度。由于实际工作时电磁中继器和地面接收装置的接收灵敏度分别为-100 dBV和-120 dBV, 考虑现场安全, 当地面信号强度低于-90 dBV时在模型左上角加入电磁中继器, 然后继续下移计算地面信号电压。若钻头还未到达完钻深度时,电磁中继器发射信号的地面信号强度低于-120 dBV, 表明电磁MWD系统的传输距离无法满足该井需要;否则,表明该井适合使用电磁MWD, 地面信号强度为-90 dBV时的井深即为电磁中继器的安装位置。
2 超高阻盐膏层中继衰减特性分析以伊朗阿瓦兹AGHA JARI区块AJ214井为例, 对所建模型进行仿真计算和结果分析。该井设计井深2 855.00 m, 采用欠平衡钻井技术钻进, 钻井液中氮气含量达20%~25%, 普通脉冲MWD无法工作;同时该井存在超高阻盐膏层, 电磁信号衰减严重, 需要安装电磁中继器确保信号传输连续。AJ214井是AGHA JARI区块应用电磁随钻测量技术的第一口试验井, 无相关历史经验数据可借鉴。
根据地质设计方案, AJ214井的地层电阻率及分层情况见图 2, 蓝线为AJ214井钻遇地层的实际电阻率, 通过拟合计算, 根据地层电阻率将地层划分为16层(图 2中红线所示), 其中大部分地层电阻率为100~1 000 Ω·m, 适宜电磁信号传输;超高阻盐膏层主要分布在1 691.00~2 300.00 m井段, 电阻率高达1.0×104~5.0×105 Ω·m。

|
| 图 2 AJ214井地层电阻率分层情况 Fig.2 Formation resistivity of Well AJ214 |
使用5种较常用频率的载波, 对所建模型进行仿真计算, 得到了该井在地面接收到的电磁MWD和电磁中继器信号强度与井深之间的关系曲线,见图 3和图 4。

|
| 图 3 地面接收到的电磁MWD信号强度与井深的关系 Fig.3 Relationship curves between surface EM-MWD signal intensity and well depth |
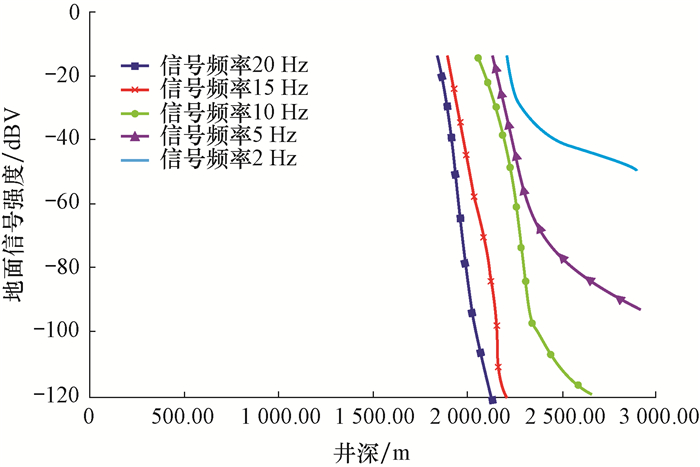
|
| 图 4 地面接收到的电磁中继器信号强度与井深的关系 Fig.4 Relationship curves between surface Repeater signal intensity and well depth |
从图 3可以看出, AJ214井中不加装电磁中继器时, 电磁MWD信号频率分别为2, 5, 10, 15和20 Hz的传输距离分别为2 540.00, 2 227.00, 2 160.00, 1 980.00和1 900.00 m, 说明在地层电阻率和其他参数都相同的环境中, 信号载波频率越低, 衰减速度越慢, 地层穿透性也越强, 这与现场应用数据所显示的规律相一致。同时, 结合图 2和图 3可以看出, 电磁信号在地层电阻率适宜的0~1 700.00 m井段衰减比较缓慢, 进入井深1 700.00 m以深超高阻盐膏层后电磁信号迅速衰减。该井设计井深为2 855.00 m, 因此只依靠电磁MWD传输频率为2~20 Hz的信号都无法成功传送至地面。
从图 4可以看出,加装电磁中继器进行信号转发后, 地面信号幅度会增强, 此时由于2 120.00~2 220.00 m井段盐膏层5.0×105 Ω·m超高电阻率的衰减影响, 10, 15和20 Hz信号的传输距离分别为2 700.00, 2 190.00和2 117.00 m, 无法成功传送至地面;5和2 Hz信号的有效传输距离均超过设计井深2 855.00 m, 但5 Hz信号在井底时, 地面接收到的信号强度仅有-91.2 dBV, 非常微弱, 为保证施工质量, 推荐使用2 Hz信号进行传输, 此时电磁中继器安装位置与电磁MWD的距离大约为2 200.00 m。
仿真分析结果表明, 超高阻盐膏层会导致电磁MWD和电磁中继器发出的信号产生断崖式衰减, 加装电磁中继器是确保超高阻地区电磁随钻测量系统顺利应用的必要手段。为验证算法效率, 采用经典有限元算法重新计算图 1中的模型, 并获得了自适应HP有限元算法和经典有限元算法求解效率的对比曲线(见图 5), 可以看出自适应HP有限元算法的计算误差收敛至0.01%时的收敛时间为128 s, 而经典有限元算法耗时387 s才能收敛至计算误差0.09%, 且精度无法进一步提高。因此, 计算精度要求较高时, 自适应HP有限元算法具有明显优势。
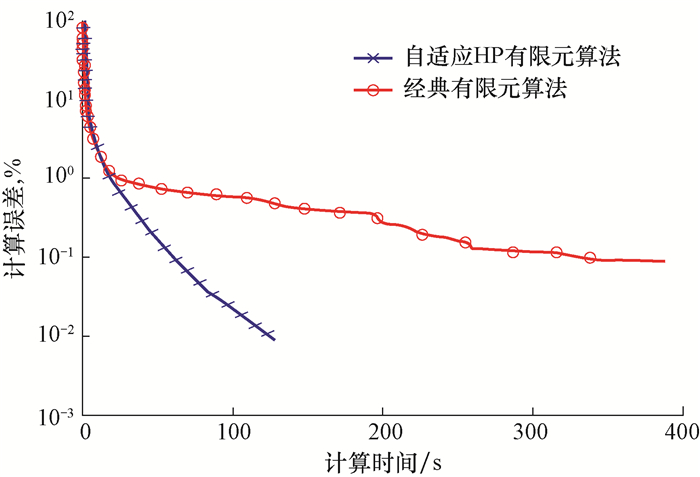
|
| 图 5 2种有限元算法的计算效率对比 Fig.5 Correlation curve for two finite element algorithms' computational efficiency |
AJ214井实际施工前期,地面接收到的电磁MWD信号一直处于一个正常衰减的过程, 0~1 700.00 m低电阻率井段的地面信号幅度从-2~0 dBV缓慢衰减至约-10~-8 dBV;进入井深1 700.00 m以深盐膏层后, 地面信号幅度锐减至约-70~-60 dBV, 但地面接收机仍能正常接收信号;由于电磁信号衰减严重, 钻至井深2 123.00 m时, 在距离电磁MWD 2 107.00 m处加装电磁中继器, 此时地面可同时接收到电磁中继器和电磁MWD信号;钻至井深2 700.00 m时, 接收不到电磁MWD信号;钻至井深2 856.00 m完钻时, 地面接收到的电磁中继器信号强度约为-53 dBV, 整个施工过程中数据传输连续, 仪器工作稳定, 满足现场定向施工要求。仪器实际应用效果和仿真结果基本一致, 电磁MWD传输距离预测准确率超过90%。
4 结论1) 超高阻盐膏层会导致电磁MWD和电磁中继器的发射信号产生-50 dBV以上的断崖式衰减。在合适位置加装电磁中继器是确保井下电磁信号连续传输、解决超高阻盐膏层地区电磁MWD传输问题的必要手段。
2) 利用基于局部求解域的有限元迭代网格模型和自适应HP有限元计算方法, 分析随钻电磁中继衰减特性, 从而预测井下电磁中继器的安装位置, 预测结果与实际工况相符, 能够满足现场施工前对电磁随钻测量可行性应用评价和电磁中继器安装位置预判的需求。
3) 与经典有限元算法相比, 自适应HP有限元算法在收敛速度和求解精度两方面都具有较大的优势。
| [1] |
闫宏亮, 石文龙, 李琳.
随钻测量信息传输方式的发展现状综述研究[J]. 重庆科技学院学报(自然科学版), 2015, 17(6): 69–72, 83.
YAN Hongliang, SHI Wenlong, LI Lin. Research on the status and future of the MWD data transmission[J]. Journal of Chongqing University of Science and Technology (Natural Sciences Edition), 2015, 17(6): 69–72, 83. |
| [2] |
袁鹏斌, 余荣华, 欧阳志英.
无线随钻测量信息传输的现状与问题[J]. 焊管, 2010, 33(10): 65–69.
YUAN Pengbin, YU Ronghua, OUYANG Zhiying, et al. The current status and problems of wireless signal transmission in measurement while drilling[J]. Welded Pipe and Tube, 2010, 33(10): 65–69. DOI:10.3969/j.issn.1001-3938.2010.10.012 |
| [3] |
马哲, 杨锦舟, 赵金海.
无线随钻测量技术的应用现状与发展趋势[J]. 石油钻探技术, 2007, 35(6): 112–115.
MA Zhe, YANG Jinzhou, ZHAO Jinhai, et al. Status quo and development trend of MWD technique[J]. Petroleum Drilling Techniques, 2007, 35(6): 112–115. |
| [4] |
汤明, 何世明, 邢景宝, 等.
大牛地气田DP14水平井氮气泡沫钻井实践与认识[J]. 天然气工业, 2010, 30(3): 74–76.
TANG Ming, HE Shiming, XING Jingbao, et al. Practices and knowledge from nitrogen foam drilling at the Well DP-14 in the Daniudi Gas Field[J]. Natural Gas Industry, 2010, 30(3): 74–76. |
| [5] |
呼石磊, 鄢泰宁, 李晓.
地层对电磁随钻测量信号的影响研究[J]. 煤炭科学技术, 2011, 39(9): 114–117.
HU Shilei, YAN Taining, LI Xiao. Study on strata affected to electromagnetic with drilling measuring signal[J]. Coal Science and Technology, 2011, 39(9): 114–117. |
| [6] |
刘修善, 侯绪田, 涂玉林, 等.
电磁随钻测量技术现状及发展趋势[J]. 石油钻探技术, 2006, 34(5): 4–9.
LIU Xiushan, HOU Xutian, TU Yulin, et al. Developments of electromagnetic measurement while drilling[J]. Petroleum Drilling Techniques, 2006, 34(5): 4–9. |
| [7] |
李林, 弓志谦, 王磊, 等.
扩展EM-MWD传输深度及提高可靠性的方法与对策[J]. 钻采工艺, 2010, 33(4): 25–27, 38.
LI Lin, GONG Zhiqian, WANG Lei, et al. Methods of improving EM-MWD transmissive depth and reliability[J]. Drilling & Production Technology, 2010, 33(4): 25–27, 38. |
| [8] |
邵养涛, 姚爱国, 张明光.
电磁波随钻遥测技术在钻井中的应用与发展[J]. 煤田地质与勘探, 2007, 35(3): 77–80.
SHAO Yangtao, YAO Aiguo, ZHANG Mingguang. Application and development of electro-magnetic telemetry in drilling operation[J]. Coal Geology & Exploration, 2007, 35(3): 77–80. |
| [9] |
胡长翠, 张明友, 张琴, 等.
井下测试数据无线传输技术探讨[J]. 钻采工艺, 2011, 34(1): 48–51.
HU Changcui, ZHANG Mingyou, ZHANG Qin, et al. Research on wireless telemetry technology of downhole test data[J]. Drilling & Production Technology, 2011, 34(1): 48–51. |
| [10] |
胡越发, 杨春国, 高炳堂.
井下电磁中继传输技术研究及应用[J]. 科技导报, 2015, 33(15): 66–71.
HU Yuefa, YANG Chunguo, GAO Bingtang. Research and application of downhole electromagnetic relay transmission technology[J]. Science & Technology Review, 2015, 33(15): 66–71. DOI:10.3981/j.issn.1000-7857.2015.15.010 |
| [11] |
郑俊华, 宗艳波, 钱德儒, 等.
井下环境模拟试验装置研制[J]. 科学技术与工程, 2017, 17(8): 21–25.
ZHENG Junhua, ZONG Yanbo, QIAN Deru, et al. Development of downhole environment simulation test equipment[J]. Science Technology and Engineering, 2017, 17(8): 21–25. |
| [12] |
李勇华, 杨锦舟, 杨震, 等.
随钻电阻率地层边界响应特征分析及应用[J]. 石油钻探技术, 2016, 44(6): 111–116.
LI Yonghua, YANG Jinzhou, YANG Zhen, et al. The analysis and application of formation interface response characteristics of the resistivity LWD tool[J]. Petroleum Drilling Techniques, 2016, 44(6): 111–116. |
| [13] |
李翠, 高德利, 刘庆龙, 等.
邻井随钻电磁测距防碰计算方法研究[J]. 石油钻探技术, 2016, 44(5): 52–59.
LI Cui, GAO Deli, LIU Qinglong, et al. A method of calculating of avoiding collisions with adjacent wells using electromagnetic ranging surveying while drilling tools[J]. Petroleum Drilling Techniques, 2016, 44(5): 52–59. |
| [14] |
解茜草, 赵志峰.
随钻电磁波测井响应时域有限差分数值模拟[J]. 计量与测试技术, 2014, 41(8): 1–3.
XIE Xicao, ZHAO Zhifeng. A study on modeling of electromagnetic wave propagation resistivity logging tool based on the FDTD method[J]. Metrology & Measurement Technique, 2014, 41(8): 1–3. |
| [15] |
陈晓晖, 刘得军, 刘得芳, 等.
随钻电阻率测量系统响应模拟算法探讨[J]. 电子测量技术, 2009, 32(6): 21–26.
CHEN Xiaohui, LIU Dejun, LIU Defang, et al. Discussion on methods of simulation for resistivity logging-while-drilling (LWD) measurements[J]. Electronic Measurement Technology, 2009, 32(6): 21–26. |
| [16] |
胡松, 王晓畅, 孔强夫.
水平井随钻电磁波电阻率数值模拟[J]. 科学技术与工程, 2017, 17(14): 59–66.
HU Song, WANG Xiaochang, KONG Qiangfu. Numerical simulation of LWD resistivity in horizontal wells[J]. Science Technology and Engineering, 2017, 17(14): 59–66. DOI:10.3969/j.issn.1671-1815.2017.14.009 |
| [17] |
杨震, 肖红兵, 李翠.
随钻方位电磁波仪器测量精度对电阻率及界面预测影响分析[J]. 石油钻探技术, 2017, 45(4): 115–120.
YANG Zhen, XIAO Hongbing, LI Cui. Impacts of accuracy of azimuthal electromagnetic logging-while-drilling on resistivity and interface prediction[J]. Petroleum Drilling Techniques, 2017, 45(4): 115–120. |
| [18] |
倪卫宁, 张晓彬, 万勇, 等.
随钻方位电磁波电阻率测井仪分段组合线圈系设计[J]. 石油钻探技术, 2017, 45(2): 115–120.
NI Weining, ZHANG Xiaobin, WAN Yong, et al. The design of the coil system in LWD tools based on azimuthal electromagnetic-wave resistivity combined with sections[J]. Petroleum Drilling Techniques, 2017, 45(2): 115–120. |




