2. 中国石油华北油田分公司第三采油厂, 河北河间 062450
2. Third Oil Production Plant of PetroChina Huabei Oilfield Company, Hejian, Hebei, 062450, China
关于Karl Terzaghi提出的有效应力计算公式(文中简称Terzaghi公式)是否精确[1-9]、能否仅用岩石孔隙度关联岩石孔隙膨胀系数与岩石骨架压缩系数[10-26],国内多位专家对此进行了大量的探讨,但没有一个明确的结论。同时,在研究岩石的外观体积、孔隙度和渗透率随孔隙压力和环境压力的变化规律时,既不可假设基质岩石颗粒尺寸不可压缩(即不可假设基质岩石颗粒为刚性),也不可假设基质岩石颗粒体积不可压缩(即不可假设基质岩石颗粒可变形但体积不变),还不可假设基质岩石颗粒与孔隙等比例变形,否则计算结果将会出现很大误差,甚至得出荒谬的结论。为了解决上述问题,避免认识混乱以更好地表征油藏中岩石体积胀缩、孔隙体积胀缩和渗透率增减等特性,笔者对Terzaghi公式存在的问题进行了分析,并总结了仅用岩石孔隙度关联岩石孔隙鼓胀系数与岩石骨架压缩系数的讨论情况,认为产生争论和错误认识的关键问题是概念混乱以及对工程、力学和数学问题认识不清。为此,提出了岩石鼓胀系数、岩石孔隙鼓胀系数、岩石渗透率鼓增系数、岩石压缩系数、岩石孔隙压缩系数和岩石渗透率压减系数等6个概念,并给出了其物理意义及表达式,以纠正以往文献中的概念和公式错误。
1 主要问题的讨论综述 1.1 关于Terzaghi公式的讨论Karl Terzaghi是第一个提出土力学有效应力概念的人,并给出了计算公式[27]:
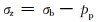
|
(1) |
式中:σz为有效压应力,Pa;σb为地层压应力(即上覆岩层压力),Pa;pp为孔隙流体压力,Pa。
文献[1-5]论证了应用于多孔介质的Terzaghi公式是错误的。原因是,如果式(1)成立,则孔隙流体压力的作用面积应该是100%,没有岩石骨架存在;没有岩石骨架存在,也就没有岩石了。岩石孔隙内有液体压力,有骨架压应力,共同承受上覆岩层压力。三者的关系应该为[1-3, 5]:
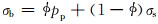
|
(2) |
式中:φ为岩石的孔隙度;σs为岩石骨架(基岩)内部的压应力,Pa。
文献[7]指出,在文献[1-3]发表以前有些文献就使用过式(2),并认为1982年苏联学者提出并被学术界广泛使用的岩石有效应力计算公式才是正确的:
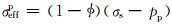
|
(3) |
式中:σeffp也称为有效压应力,Pa。
实际上,式(3)也是错误的,其错误与式(1)的错误基本一样。例如,当孔隙度为0时,pp应该不会对σeffp有影响,即σeffp=σb=σs,而式(3)则变为:σeffp=σb-pp,这明显是矛盾的。
文献[8-11]的岩石有效应力计算公式中也有σb-pp项,因而也是错误的。
1.2 关于仅用岩石孔隙度关联岩石孔隙鼓胀系数与岩石骨架压缩系数的讨论文献[12]试图先用岩石骨架的材料力学性质计算岩石骨架压缩系数,然后用岩石骨架压缩系数和岩石孔隙度计算岩石压缩系数(应为岩石孔隙鼓胀系数,作者注),以期用测量岩石骨架的材料力学性质来取代测量岩石压缩系数(应为岩石孔隙鼓胀系数,作者注)。其主要推导过程如下。
岩石外观体积等于岩石骨架体积与岩石孔隙体积之和,即:
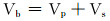
|
(4) |
式中:Vb为岩石外观体积,m3;Vp为岩石孔隙体积,m3;Vs为岩石骨架体积,m3。
定义岩石压缩系数(应为岩石孔隙鼓胀系数,作者注)为:围压为常数,孔隙压力增加一个单位压力时孔隙体积的变化率,其表达式为:

|
(5) |
式中:Cp为岩石压缩系数(应为岩石孔隙鼓胀系数,作者注),Pa-1。
岩石压缩系数之所以应为岩石孔隙鼓胀系数,是因为随着岩石孔隙压力的增加,孔隙体积会增加,而岩石压缩系数并不能体现出孔隙体积增加的特性。
定义岩石骨架压缩系数为岩石骨架平均压力增加一个单位压力时的体积变化率,其表达式为:

|
(6) |
式中:Cs为岩石骨架压缩系数,Pa-1。
根据弹性力学,对于岩石任意一点,岩石骨架压缩系数可以表示为:

|
(7) |
式中:ν为岩石骨架泊松比;Es为岩石骨架弹性模量,Pa。
假设:1)岩石的平均压应力为常数且由式(2)计算;2)岩石骨架与孔隙等比例胀缩;3)孔隙度为常数。则可得岩石压缩系数:
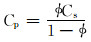
|
(8) |
根据式(8),当φ<0.5时, Cp<Cs,即孔隙介质比基质更难压缩,这显然是错误的。为此,很多人对该问题进行了讨论,甚至是争论[13-24],但均未给出一个令人信服的结果。
2 存在问题的原因分析笔者认为,之所以产生上述争论,关键问题是概念混乱以及对工程、力学和数学问题认识不清。
2.1 概念混乱在上述争论中存在3方面的问题:
1) 同一名词,不同作者表达不同意义。例如文献[13]与文献[12, 14, 17, 21]中,“岩石压缩系数”的意义不同。
2) 同一意义,不同作者用不同概念表达。例如文献[12]中的“岩石压缩系数”与文献[13]和文献[15]中的“岩石孔隙压缩系数”表达的是同一意义。
3) 文字定义与数学定义不一致。例如文献[15]中的“岩石压缩系数”的文字定义与数学定义(即原文中的式(2))不一致。
因为争论太多,这里就不一一列举了,具体见文献[13-24]。
2.2 对工程、力学和数学问题认识不清在推导式(8)时的3个假设以及文献[25-26]在研究孔隙压缩系数时“岩石颗粒不可压缩”的假设,是不合理的。
1) “岩石颗粒不可压缩”的假设不合理。若岩石颗粒不可压缩则岩石不可压缩,即岩石为刚体,则其体积、孔隙度和渗透率不会随孔隙压力和环境压力的变化而变化,永远是个常数。如果是岩石颗粒体积不可压缩的误写,则孔隙体积变化量等于岩石外观体积的变化量,在研究孔隙度极高(接近于1)的多孔介质的孔隙度随孔隙压力和环境压力的变化时尚有一定精度;在研究孔隙度极低的多孔介质(例如页岩)的孔隙度随孔隙压力和环境压力的变化时误差太大。
2) “岩石骨架与孔隙等比例胀缩”的假设不合理。无论是孔隙压力变化还是围压变化引起的孔隙胀缩率都要远大于岩石骨架的胀缩率,这才符合最小势能原理。例如吹气球,气球是个弹性体,大气压强是个常数,当人们吹气球时,气球的断面并不是等比例变化,而是空腔直径不断变大,球壁越变越薄。
3) “孔隙度是常数”的假设不合理。孔隙度是变量,不是常数。岩石力学中有一个压实的概念,即孔隙度减小。孔隙压力变化导致孔隙体积、骨架体积变化就是压实或反压实过程。文献[12]在对式(2)进行微分时得到的公式:
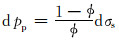
|
(9) |
是错误的,应该为:
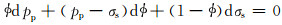
|
(10) |
式(7)成立的前提为材料是均质的和各向同性的,但岩石骨架既不是均质的也不是各向同性的,所以,对于多孔介质式(7)是不成立的。另外,很难从岩石中取出一块没有孔隙的基质来做材料力学实验,这比直接测量岩石孔隙鼓胀率的实验还难。如用其他方法取代材料力学实验,则数据的可靠性值得怀疑。
4) “岩石的平均压应力为常数”的假设,在油藏内一般不严格成立。在实验室条件下,可以控制围压,使岩石的平均压应力为常数。但是,在油藏内,局部注液体必然引起注入部位及周围的平均压应力增高,所以,在油藏内“岩石的平均压应力为常数”不严格成立。
由此可以看出,式(8)的目的是通过岩石孔隙度建立岩石骨架材料的材料力学性质与岩石压缩系数(应为岩石孔隙鼓胀系数,作者注)的关系,有意义但很难实现,并且该式是错误的,其他人也没有给出合理的结果。
2.3 不能仅用岩石孔隙度关联岩石压缩系数与岩石骨架压缩系数以文献[12]为基础,结合上面的讨论,可以建立方程组:
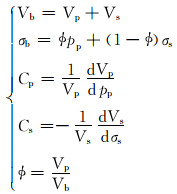
|
(11) |
该方程组共有5个方程,共有Vb, Vp, Vs, σb, φ, pp, σs, Cp和Cs等9个未知量,若没有其他附加条件,该方程组是不可能表达成Cp=f(φ, Cs)的。即使假设σb为已知常数,5个独立方程,8个未知量,也是不可能表达成Cp=f(φ, Cs)的。因此,不能仅用岩石孔隙度关联岩石压缩系数(应为岩石孔隙鼓胀系数,作者注)与岩石骨架压缩系数。
3 解决问题的措施探讨规范相应名词的定义可以解决油气藏多孔岩石鼓胀压缩特性表征方面出现的上述混乱现象,因此,应该以弹性力学和岩石力学为基础,根据命名规则[28],重新定义相关概念。
在石油工程中,孔隙压力和围压是影响岩石外观体积、孔隙度和渗透率的重要因素。如果岩石承受的三向应力不等,加上岩石具有各向异性,问题将变得十分复杂。因此,笔者仅针对围压各向相等的情况,提出了岩石鼓胀系数、岩石孔隙鼓胀系数、岩石渗透率鼓增系数、岩石压缩系数、岩石孔隙压缩系数和岩石渗透率压减系数等6个相互独立的概念,并给出了其定义。
3.1 岩石鼓胀系数岩石鼓胀系数是指在围压σb为常数σbc时,孔隙压力pp从ppc增加一个单位压力时,岩石外观体积的变化率,可以表示为:
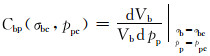
|
(12) |
式中:Cbp(σbc, ppc)为岩石鼓胀系数,Pa-1;ppc为实验孔隙压力,Pa;σbc为实验围压,Pa。
岩石鼓胀意指孔隙内部流体压力致使外观体积增加,不会产生歧义。该系数可以用来计算地层的膨胀和沉陷及地应力的变化。
用Cbp(σbc, ppc)来表示岩石鼓胀系数,不是表示围压和孔隙压力都一直为常数,而是因为Cbp是σbc和ppc的函数,一般不是常数。这种表达就像数学中的
岩石孔隙鼓胀系数是指在围压σb为常数σbc时,孔隙压力pp从ppc增加一个单位压力时,孔隙体积的变化率,可以表示为:

|
(13) |
式中:Cpp(σbc, ppc)为岩石孔隙鼓胀系数,Pa-1。
该系数是指因孔隙压力增加,导致孔隙空间增加,不会产生歧义,可以用来计算孔隙体积的变化量。
3.3 岩石渗透率鼓增系数岩石渗透率鼓增系数是指在围压σb为常数σbc时,孔隙压力pp从ppc增加一个单位压力时,渗透率的变化率,可以表示为:
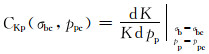
|
(14) |
式中:CKp(σbc, ppc)为岩石渗透率鼓增系数,Pa-1;K为渗透率,m2。
该系数是指因孔隙内压力增加,使孔隙直径增加,最终导致渗透率增加,不会产生歧义,可以用来计算渗透率的变化量。
3.4 岩石压缩系数岩石压缩系数是指在孔隙压力pp为常数ppc时,围压σb从σbc增加一个单位压力时,岩石外观体积的变化率,可以表示为:
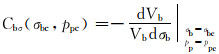
|
(15) |
式中:Cbσ(σbc, ppc)为岩石压缩系数,Pa-1。
该系数的定义与材料力学和弹性力学中的定义类似,指随着岩石围压的增加,岩石外观体积减小,可以用来计算地层的膨胀和沉陷及地应力的变化。
3.5 岩石孔隙压缩系数岩石孔隙压缩系数是指在孔隙压力pp为常数ppc时,围压σb从σbc增加一个单位压力时,孔隙体积的变化率,可以表示为:
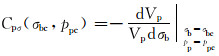
|
(16) |
式中:Cpσ(σbc, ppc)为岩石孔隙压缩系数,Pa-1。
该系数是指因岩石围压增加,导致孔隙空间减小,不会产生歧义,可以用来计算孔隙体积的变化量。
3.6 岩石渗透率压减系数岩石渗透率压减系数是指在孔隙压力pp为常数ppc时,围压σb从σbc增加一个单位压力时,岩石渗透率的变化率,可以表示为:

|
(17) |
式中:CKσ(σbc, ppc)为岩石渗透率压减系数,Pa-1。
该系数是指因岩石围压增加,使孔隙直径减小,最终导致渗透率降低,不会产生歧义,可以用来计算渗透率的变化量。
4 结论1) Terzaghi公式是错误的。
2) 不可仅用岩石孔隙度关联岩石孔隙鼓胀系数与岩石骨架压缩系数,且测量岩石骨架压缩系数比测量岩石孔隙鼓胀系数更难。
3) 在研究岩石的外观体积、孔隙度和渗透率随孔隙压力和环境压力的变化规律时,既不可假设基质岩石颗粒尺寸不可压缩,也不可假设基质岩石颗粒体积不可压缩,还不可假设基质岩石颗粒与孔隙等比例变形。否则,会产生逻辑问题或难以置信的误差。
4) 提出的岩石鼓胀系数、岩石孔隙鼓胀系数、岩石渗透率鼓增系数、岩石压缩系数、岩石孔隙压缩系数和岩石渗透率压减系数等6个概念可以解决多孔岩石鼓胀压缩特性表征方面出现的混乱现象。
| [1] |
李传亮.
岩石压缩系数测量方法的理论研究[J]. 石油与天然气地质, 1998, 19(4): 280–285.
LI Chuanliang. A theoretical study on measurement of rock compacting factors[J]. Oil & Gas Geology, 1998, 19(4): 280–285. DOI:10.11743/ogg19980403 |
| [2] |
李传亮, 孔祥言, 徐献芝, 等.
多孔介质的双重有效应力[J]. 自然杂志, 1999, 21(5): 288–291.
LI Chuanliang, KONG Xiangyan, XU Xianzhi, et al. Double effective stresses of porous media[J]. Chinese Journal of Nature, 1999, 21(5): 288–291. |
| [3] |
李传亮.
多孔介质的应力关系方程:答周大晨先生[J]. 新疆石油地质, 2002, 23(2): 163–164.
LI Chuanliang. Equations for stress relations in porous medium:in reply to Mr.Zhou Dachen[J]. Xinjiang Petroleum Geology, 2002, 23(2): 163–164. |
| [4] |
李敬元, 李子丰.
渗流作用下井筒周围岩石内的弹塑性应力分布规律及井壁稳定条件[J]. 工程力学, 1997, 14(1): 131–137.
LI Jingyuan, LI Zifeng. Rock elastic-plastic stresses around a wellbore and wellbore stability under permeation osmosis[J]. Engineering Mechanics, 1997, 14(1): 131–137. |
| [5] |
李子丰.
基岩应力公式的探讨[J]. 石油钻采工艺, 2001, 23(3): 41.
LI Zifeng. Discussion on the matrix stress formula[J]. Oil Drilling & Production Technology, 2001, 23(3): 41. |
| [6] |
陈庭根, 管志川.
钻井工程理论与技术[M]. 东营: 石油大学出版社, 2000: 8.
CHEN Tinggen, GUAN Zhichuan. Drilling engineering theory and technology[M]. Dongying: Petroleum University Press, 2000: 8. |
| [7] |
窦宏恩.
油田开发中岩石压缩系数和孔隙度相关问题探讨[J]. 新疆石油地质, 2012, 33(5): 617–622.
DOU Hongen. Discussion about rock compressibility and porosity applied in oilfield development[J]. Xinjiang Petroleum Geology, 2012, 33(5): 617–622. |
| [8] |
张睿, 宁正福, 杨峰, 等.
页岩应力敏感实验研究及影响因素分析[J]. 岩石力学与工程学报, 2015, 34(增刊1): 2617–2622.
ZHANG Rui, NING Zhengfu, YANG Feng, et al. Experimental study of stress sensitivity of shale reservoirs[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(supplement 1): 2617–2622. |
| [9] | ZHANG Rui, NING Zhengfu, YANG Feng, et al. Impacts of nanopore structure and elastic properties on stress-dependent permeability of gas shales[J]. Journal of Natural Gas Science and Engineering, 2015, 26: 1663–1672. DOI:10.1016/j.jngse.2015.02.001 |
| [10] |
蔡新树, 陈勉, 金衍, 等.
各向异性多重孔隙介质有效应力定律[J]. 工程力学, 2009, 26(4): 57–60.
CAI Xinshu, CHEN Mian, JIN Yan, et al. An effective stress law for anisotropic multi-porosity media[J]. Engineering Mechanics, 2009, 26(4): 57–60. |
| [11] |
陈茜, 骆亚生, 程大伟.
非饱和土有效应力及其参数的确定[J]. 工程力学, 2013, 30(6): 340–345.
CHEN Xi, LUO Yasheng, CHENG Dawei. Effective stress and parameters of unsaturated loess[J]. Engineering Mechanics, 2013, 30(6): 340–345. |
| [12] |
李传亮.
岩石压缩系数与孔隙度的关系[J]. 中国海上油气(地质), 2003, 17(5): 355–358.
LI Chuanliang. The relationship between rock compressibility and porosity[J]. China Offshore Oil and Gas(Geology), 2003, 17(5): 355–358. |
| [13] |
罗瑞兰.
对"低渗透储层不存在强应力敏感"观点的质疑[J]. 石油钻采工艺, 2006, 28(2): 78–80.
LUO Ruilan. Queries to the viewpoint low permeability reservoirs have not the characteristics of strong stress sensitivity[J]. Oil Drilling & Production Technology, 2006, 28(2): 78–80. |
| [14] |
李传亮.
储层岩石的应力敏感问题:答罗瑞兰女士[J]. 石油钻采工艺, 2006, 28(6): 86–88.
LI Chuanliang. Discussion on the stress sensitivity of reservoir rocks:reply to Ms.Luo Ruilan[J]. Oil Drilling & Production Technology, 2006, 28(6): 86–88. |
| [15] |
窦宏恩.
质疑不存在启动压力之观点[J]. 特种油气藏, 2009, 16(1): 53–57.
DOU Hongen. The viewpoint of there isn't threshold pressure is doubted[J]. Special Oil and Gas Reservoirs, 2009, 16(1): 53–57. |
| [16] |
窦宏恩, 白喜俊.
低渗透和高渗透储层都存在应力敏感性[J]. 石油钻采工艺, 2009, 31(2): 121–124.
DOU Hongen, BAI Xijun. Stress sensitivity consists in low permeability and middle-high permeability reservoirs[J]. Oil Drilling & Production Technology, 2009, 31(2): 121–124. |
| [17] |
李传亮.
低渗透储层很特殊吗:回应窦宏恩先生[J]. 特种油气藏, 2011, 18(5): 131–134.
LI Chuanliang. Are low permeability reservoirs very special:reply to Mr.Dou Hongen[J]. Special Oil and Gas Reservoirs, 2011, 18(5): 131–134. |
| [18] |
窦宏恩.
岩石孔隙体积压缩系数表达式推导:兼答《低渗透储层很特殊吗》一文作者[J]. 特种油气藏, 2012, 19(4): 149–150.
DOU Hongen. Derivation of equations of rock pore volume compressibility:a reply to the author of is low permeability reservoir very special?[J]. Special Oil and Gas Reservoirs, 2012, 19(4): 149–150. |
| [19] |
贾碧霞, 徐予勖.
岩石压缩系数的新求解方法:对"岩石压缩系数对油藏动态储量计算结果的影响"中压缩系数求解方法的质疑[J]. 青海石油, 2010, 28(2): 29–31.
JIA Bixia, XU Yuxu. A new method to solve rock compressibility[J]. Qinghai Oil, 2010, 28(2): 29–31. |
| [20] |
王厉强, 李正科, 申红, 等.
实测岩石孔隙压缩系数偏高原因再分析:与李传亮教授商榷[J]. 新疆石油地质, 2011, 32(1): 102–103.
WANG Liqiang, LI Zhengke, SHEN Hong, et al. A discussion on results interpretation again of higher measured rock compressibility[J]. Xinjiang Petroleum Geology, 2011, 32(1): 102–103. |
| [21] |
李传亮.
储集层岩石的压缩系数公式:回应王厉强博士[J]. 新疆石油地质, 2012, 33(1): 125–126.
LI Chuanliang. The formulae of rock compressibility of reservoirs:reply to Dr.Wang Liqiang[J]. Xinjiang Petroleum Geology, 2012, 33(1): 125–126. |
| [22] |
王厉强, 李正科, 袁昭, 等.
再论储集层岩石的压缩问题:对《储集层岩石的压缩问题》一文的不同看法[J]. 新疆石油地质, 2012, 33(6): 379–381.
WANG Liqiang, LI Zhengke, YUAN Zhao, et al. Re-discussion on the compression of reservoir rocks[J]. Xinjiang Petroleum Geology, 2012, 33(6): 379–381. |
| [23] |
李传亮.
岩石的压缩系数问题:再与王厉强博士商榷[J]. 新疆石油地质, 2013, 34(3): 354–356, 360.
LI Chuanliang. Compressibility of reservoir rocks:re-discussion with Dr.Wang Liqiang[J]. Xinjiang Petroleum Geology, 2013, 34(3): 354–356, 360. |
| [24] |
陈元千, 邹存友.
三种岩石压缩系数关系的推导与对比[J]. 新疆石油地质, 2012, 33(4): 459–460.
CHEN Yuanqian, ZOU Cunyou. Deduction and comparison of relationships among three kinds of rock compressibility factors[J]. Xinjiang Petroleum Geology, 2012, 33(4): 459–460. |
| [25] |
张睿, 宁正福, 杨峰, 等.
页岩应力敏感实验与机理[J]. 石油学报, 2015, 36(2): 224–231, 237.
ZHANG Rui, NING Zhengfu, YANG Feng, et al. Shale stress sensitivity experiment and mechanism[J]. Acta Petrolei Sinica, 2015, 36(2): 224–231, 237. DOI:10.7623/syxb201502012 |
| [26] | ZHANG Rui, NING Zhengfu, YANG Feng, et al. A laboratory study of the porosity-permeability relationships of shale and sandstone under effective stress[J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 81: 19–27. |
| [27] | TERZAGHI K. Theoretical soil mechanics[M]. New York: John Wiley & Sons, 1943: 11-13. |
| [28] | LI Zifeng, LI Xuejiao. Semantic issues with the word "anti" in particle physics[J]. Physics Essays, 2012, 25(3): 347–348. DOI:10.4006/0836-1398-25.3.347 |


