2. 中国石化上海海洋油气分公司勘探开发研究院, 上海 200120
2. Exploration and Development Research Institute, Sinopec Shanghai Offshore Petroleum Company, Shanghai, 200120, China
气藏见水时间预测是气藏开发的关键问题,国内外学者对边底水气藏见水时间的预测研究从2方面开展[1-16]:1) 底水锥进临界产量和水锥突破时间研究;2) 边水气藏见水时间预测研究。底水锥进临界产量和水锥突破时间的预测一般会考虑重力的影响,而边水气藏见水时间的预测只考虑水质点沿水平方向舌进,忽略储层倾角和水侵速度对见水时间的影响。但是,在实际生产过程中,沿倾角方向的重力往往会阻碍水的舌进,而水侵导致气水边界逐渐减小。因此,上述2个因素会显著影响带倾角边水气藏的见水时间。为此,笔者基于物质平衡方程及多孔介质流体渗流理论,建立了考虑储层倾角和水侵的边水气藏见水时间预测模型,以更加准确地预测带倾角边水气藏的见水时间。
1 预测模型的建立 1.1 物理模型的建立假设带倾角边水气藏的储层倾角为α,有1口生产井 (B井),在水平方向和垂直方向上与初始气水界面a点的距离分别为ra和ha,水沿着倾角方向运移,经过时间t后到达B井所在的b点,如图 1所示。
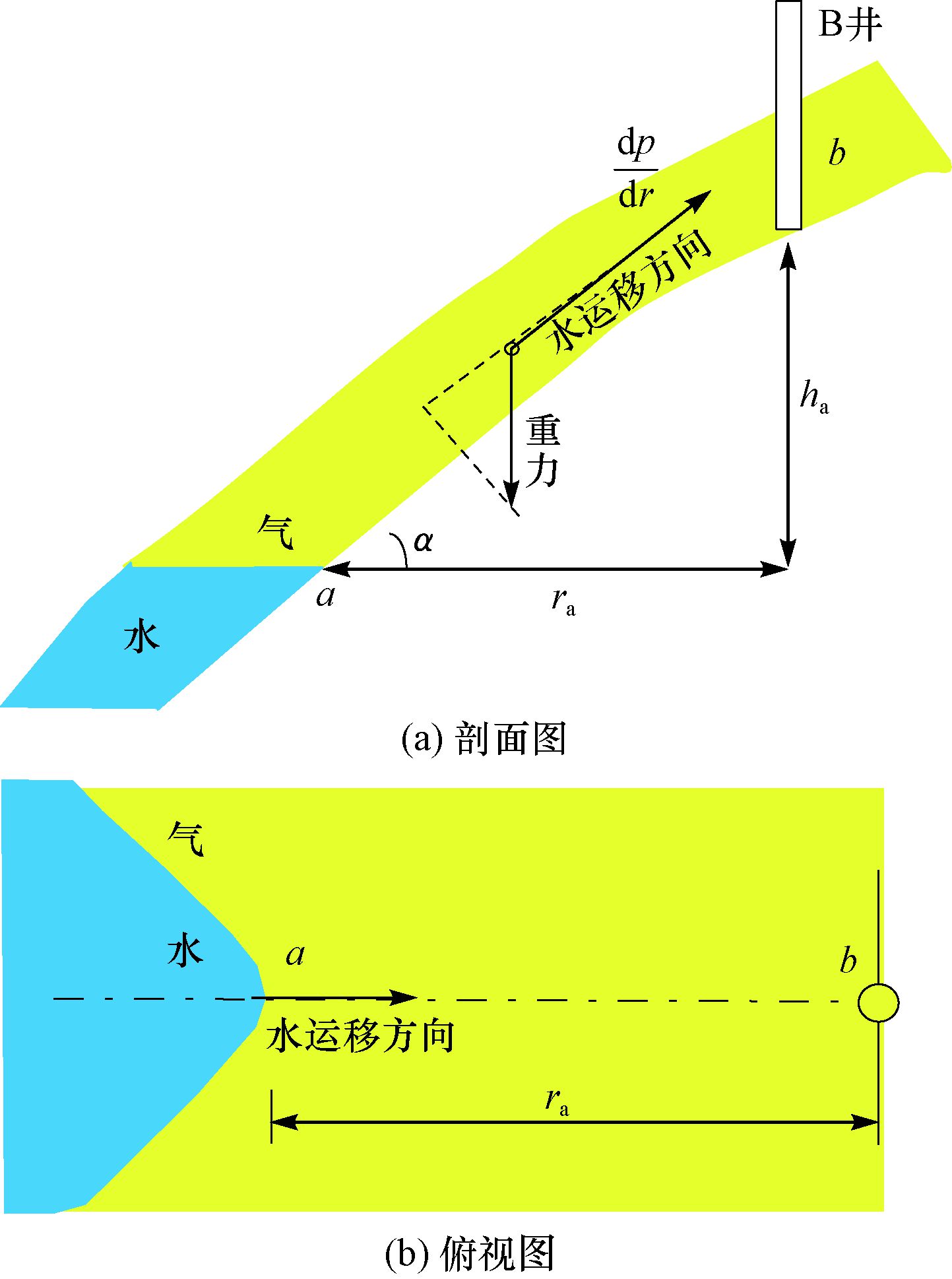
|
| 图 1 带倾角边水气藏生产井示意 Fig.1 Schematic diagram of production wells of edge-water gas reservoirs with reservoir dip |
基于渗流理论,对物理模型作如下假设:1) 均质地层;2) 水驱气以活塞方式进行,并在水侵地区形成残余气;3) 忽略毛细管压力,流动主要由黏性力和重力来控制;4) 气和水具有恒定的黏度和密度;5) 气和水的流动符合达西定律;6) 储层下部为隔层,水不能通过。流体受力特征分析表明,水受到沿倾角方向的驱动压力和重力的影响。水要沿着倾角方向流动必须先克服重力的影响,即沿倾角方向的驱动压力应该大于重力在该方向的分力,否则水无法沿着倾角方向舌进。下面具体分析气水界面处水从a点向B井所在的b点运移的过程。
考虑倾角影响的气水两相渗流公式为:
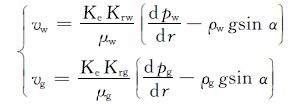
|
(1) |
式中:Ke为储层有效渗透率,mD;Krg和Krw分别为气相和水相所在储层的相对渗透率;μg和μw分别为气相和水相的黏度,mPa·s;vg和vw分别为气相和水相的流速,m/s;pg和pw分别为气相和水相所在储层的地层压力,MPa;ρg和ρw分别为气相和水相的密度,kg/m3;g为重力加速度,m/s2。
研究目的是获得水舌a点的突破时间,考虑在该点dpg/dr对水相也起作用,则需要满足条件:
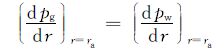
|
(2) |
结合式 (1) 和式 (2),得到水相流度和气水流度比的关系为:
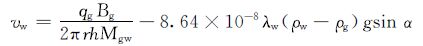
|
(3) |
式中:Mgw为气水流度比,Mgw=λg/λw;λg和λw分别为气相和水相的流度,mD/(mPa·s);qg为产气量,m3/d;Bg为气相体积系数;h为储层厚度,m。
当水相速度为0时,驱动压力等于重力,则水运移的临界边界为:
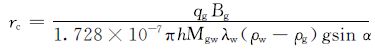
|
(4) |
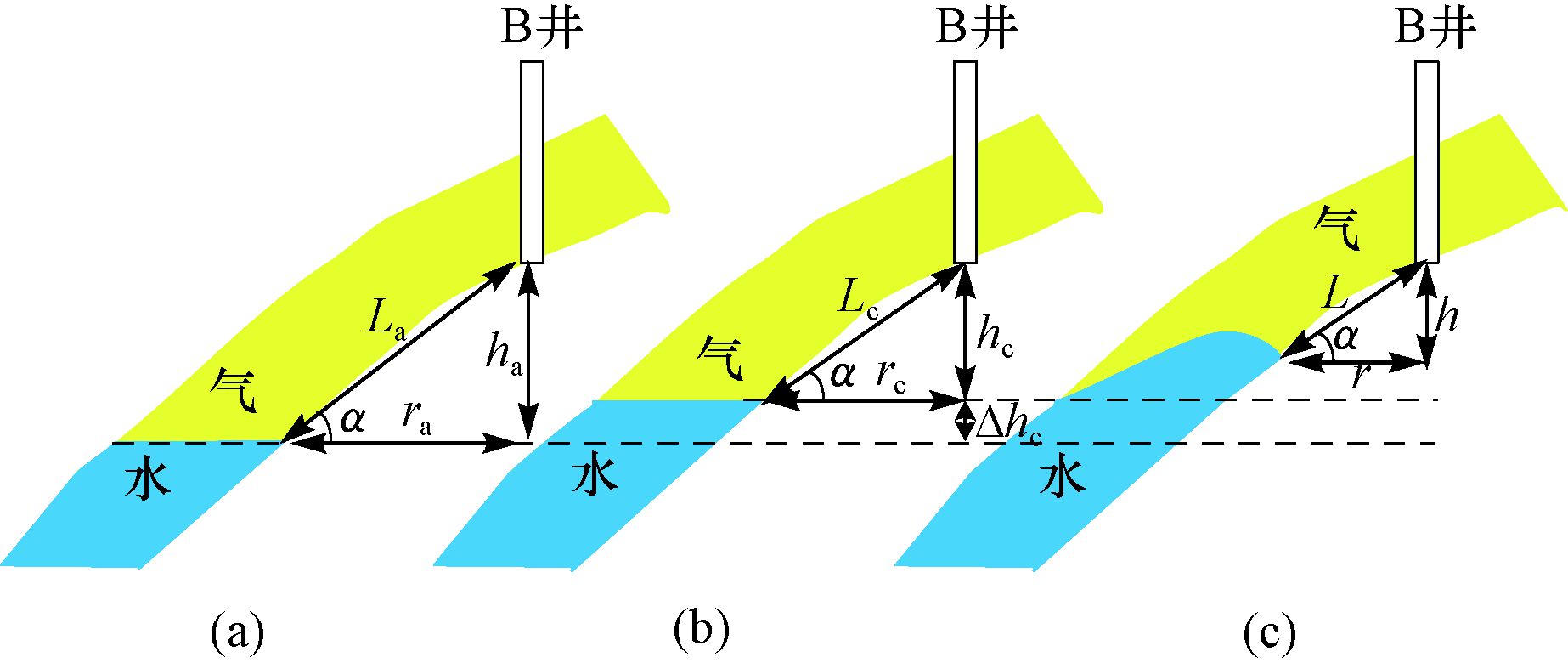
图 2为带倾角边水气藏水运移示意图。初始气水界面与井点在水平、垂直及沿倾角方向的距离分别为ra,ha和La,见图 2(a);水运移到临界边界时与井点在水平、垂直及沿倾角方向的距离分别为rc,hc和Lc,上升高度为Δhc, 见图 2(b);水从临界边界运移到近井某位置时与井点在水平、垂直及沿倾角方向的距离分别为r,h和L,见图 2(c)。由式 (4) 可知:当r>rc时,驱动压力小于重力,气体的产出导致储层亏空,水逐渐侵入储层,水侵入储层是相对稳态的过程,从图 2(a)到图 2(b)展示了水由初始气水界面侵入到临界边界的过程;当r<rc时,驱动压力大于重力,水会沿着储层倾角方向舌进,从图 2(b)到图 2(c)展示了水舌进的过程;与稳态水侵过程相比,水的舌进比较迅速。故以rc为临界边界,将水的运移过程分为水侵和水质点舌进2个阶段。
|
| 图 2 带倾角边水气藏水运移示意 Fig.2 Schematic diagram of water migration in edge-water gas reservoirs with reservoir dip |
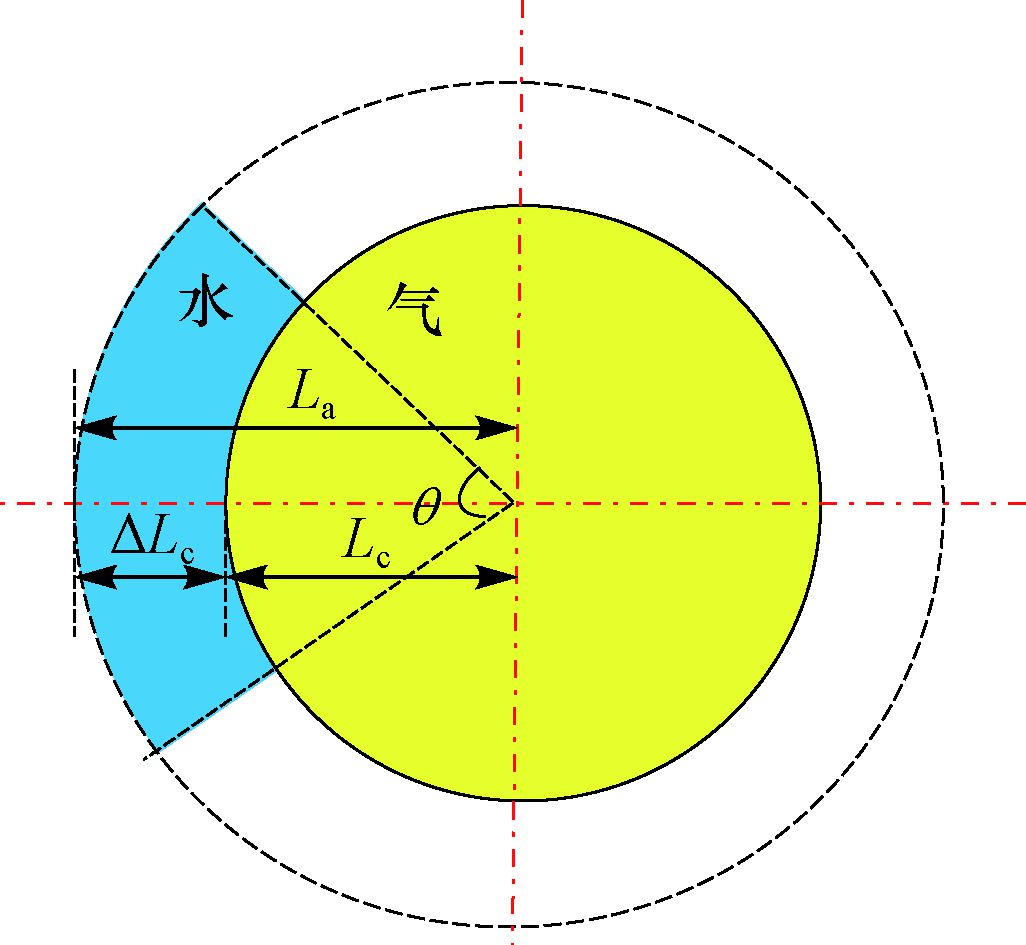
图 3为带倾角边水气藏的气水边界示意图。当气体从气藏被采出后,气藏压力下降,地层水会侵入气藏,含气半径减小,设减小量为ΔLc。假设水均匀侵入圆形储层,水侵角为θ,然后对水侵前后储层各参数的变化情况进行分析。
|
| 图 3 带倾角边水气藏水侵示意 Fig.3 Schematic diagram of water invasion in edge-water gas reservoirs with reservoir dip |
考虑束缚水、残余气以及水侵区域内岩石和束缚水体积膨胀的影响,圆形气藏中水侵入的体积为:

|
(5) |
式中:Swi,Swc和Sgr分别为初始含水饱和度、束缚水饱和度及残余气饱和度;Cw和Cf分别为水相和岩石的压缩系数,MPa-1;Δp为气藏压降,MPa;φ为孔隙度;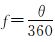
同样,当水体推进到井底后,气井开始产出地层水,根据物质平衡原理,水侵入的体积Vc也可以表示为:
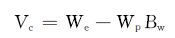
|
(6) |
式中:We为水侵量,表示侵入储层的地层水所占据的孔隙体积,104m3;Wp为累计产水量,104m3;Bw为水相体积系数。
联立式 (5) 和式 (6),可以得到水侵距离为:
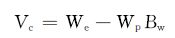
|
(7) |
根据储层倾角α可计算水体沿水平方向的运移距离Δrc和上升高度Δhc为:
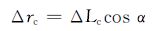
|
(8) |
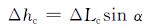
|
(9) |
考虑储层倾角的影响,当水体由气水边界推进到临界边界rc时,满足:
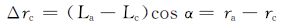
|
(10) |
记水侵速度为vw′,则水侵到临界边界的时间为:

|
(11) |
式中:vw′为水侵速度,m/s;tc为水侵到临界边界的时间,s。
1.3 边水气藏舌进阶段运移时间考虑束缚水、残余气以及水侵影响的水质点运移规律为:

|
(12) |
结合式 (3),对式 (12) 积分得水质点舌进时间为:
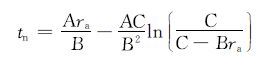
|
(13) |
式中:tn为水质点舌进时间,d;A,B,C为相关系数。
相关系数A, B, C分别可表示为:
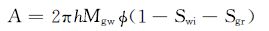
|
(14) |
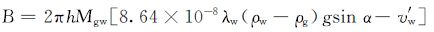
|
(15) |

|
(16) |
如果不考虑倾角和水侵的影响,式 (13) 可简化为常规气井见水时间预测模型[10-11]:
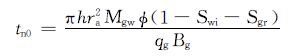
|
(17) |
式中:tn0为常规模型的气井见水时间,d。
1.4 见水时间的确定带倾角边水气藏的见水时间为水侵时间和水质点舌进时间之和,以储层半径大于rc和小于rc2个阶段对其讨论。
1) 当储层半径大于rc时,水侵速度是水运移的主要影响因素,故水从ra侵入到临界半径rc的时间为:
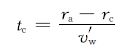
|
(18) |
2) 当储层半径小于rc时,驱动压力和沿倾角方向的重力为主要影响因素,故水从半径rc处舌进到井底的时间为:
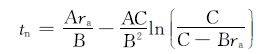
|
(19) |
则带倾角边水气藏的见水时间为:
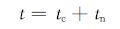
|
(20) |
假设气井距气水边界700 m,产气量10×104 m3/d,储层倾角在0°~25°,水侵速度分别为20和40 m/a,分析倾角和水侵速度对见水时间的影响。
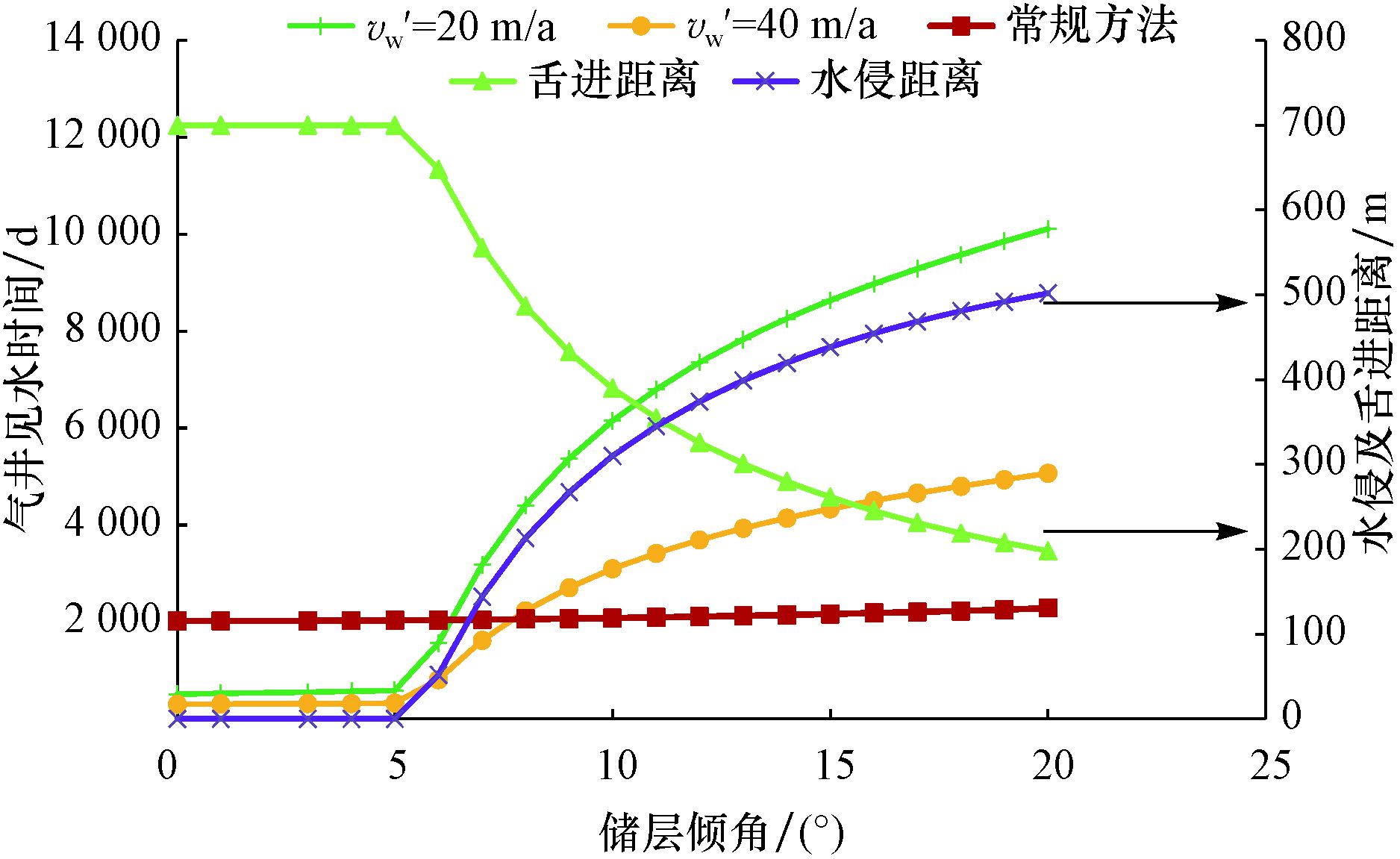
图 4为气井见水时间与倾角的关系。
|
| 图 4 气井见水时间与倾角的关系 Fig.4 Relationship of water breakthrough timing vs. dip |
由图 4可知,当倾角小于5°时,重力作用不显著,水质点舌进距离大,水质点迅速舌进至井底。当倾角大于5°时,重力作用显著,随着倾角增大,水质点舌进距离逐渐减小,水侵距离逐渐增大,见水时间也逐渐增长。此时,储层中水的运移分为2个阶段:水侵作用首先使水逐渐向井筒方向运移,当水侵到可舌进距离时,水在重力、驱动力和水侵共同作用下沿着倾角方向舌进至井筒。
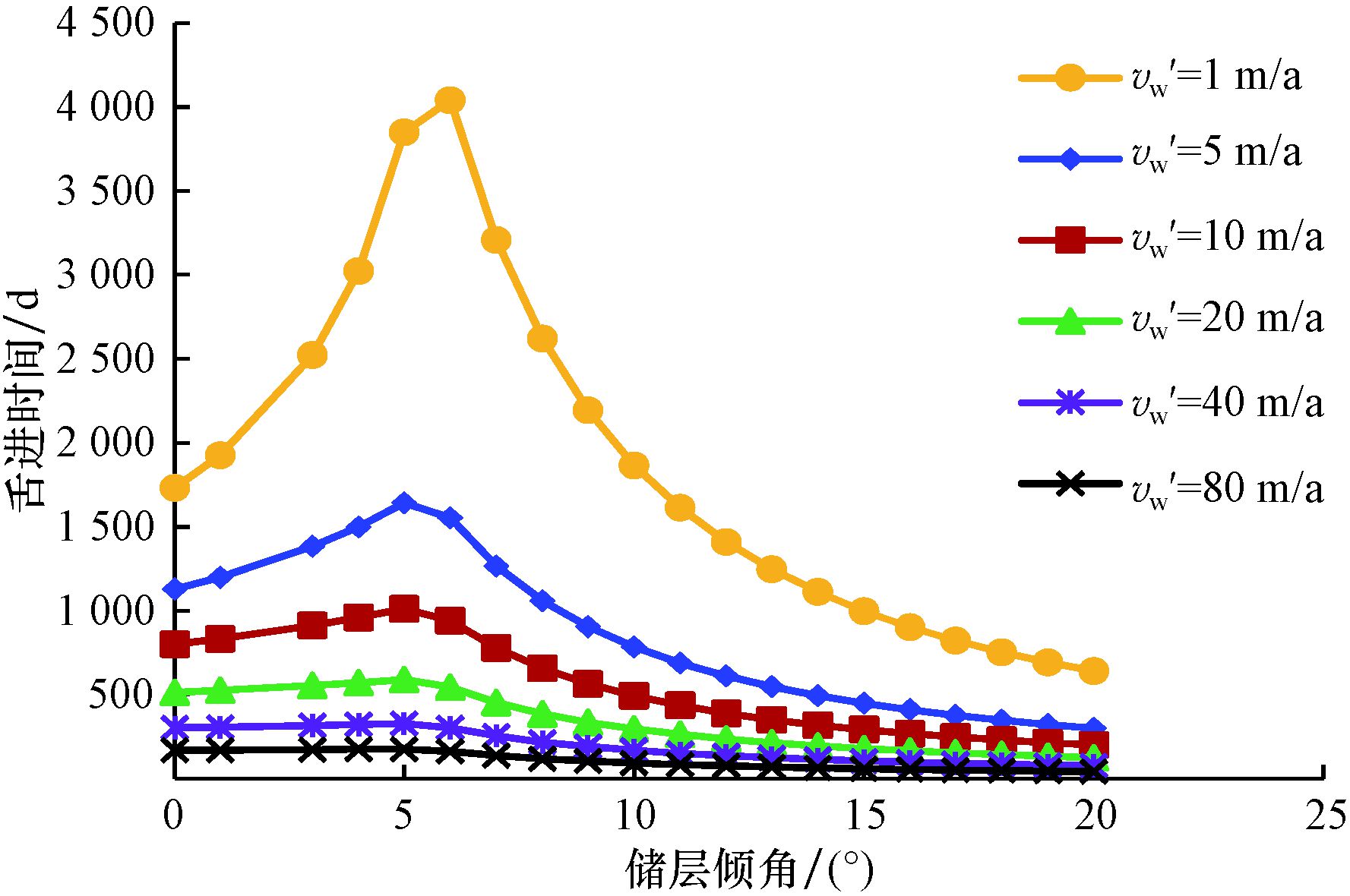
图 5为不同水侵速度下水质点舌进时间与储层倾角的关系。
|
| 图 5 不同水侵速度下舌进时间与储层倾角的关系 Fig.5 Relationship of reservoir dip vs. tonguing timing at different water invasion speed |
由图 5可知,舌进时间随储层倾角增大先增长后缩短,两者之间呈复杂非线性关系。分析认为,其原因是,当倾角较小时,舌进距离大,舌进时间长,而随着倾角增大,舌进距离逐渐减小,舌进时间越来越短。进一步分析可知,水侵速度越大,舌进时间越短,其原因是,当水侵速度较小时,水的运移主要靠水质点的运动,随着水侵速度增大,水侵对水质点运移的影响越来越大,故舌进时间越来越短。
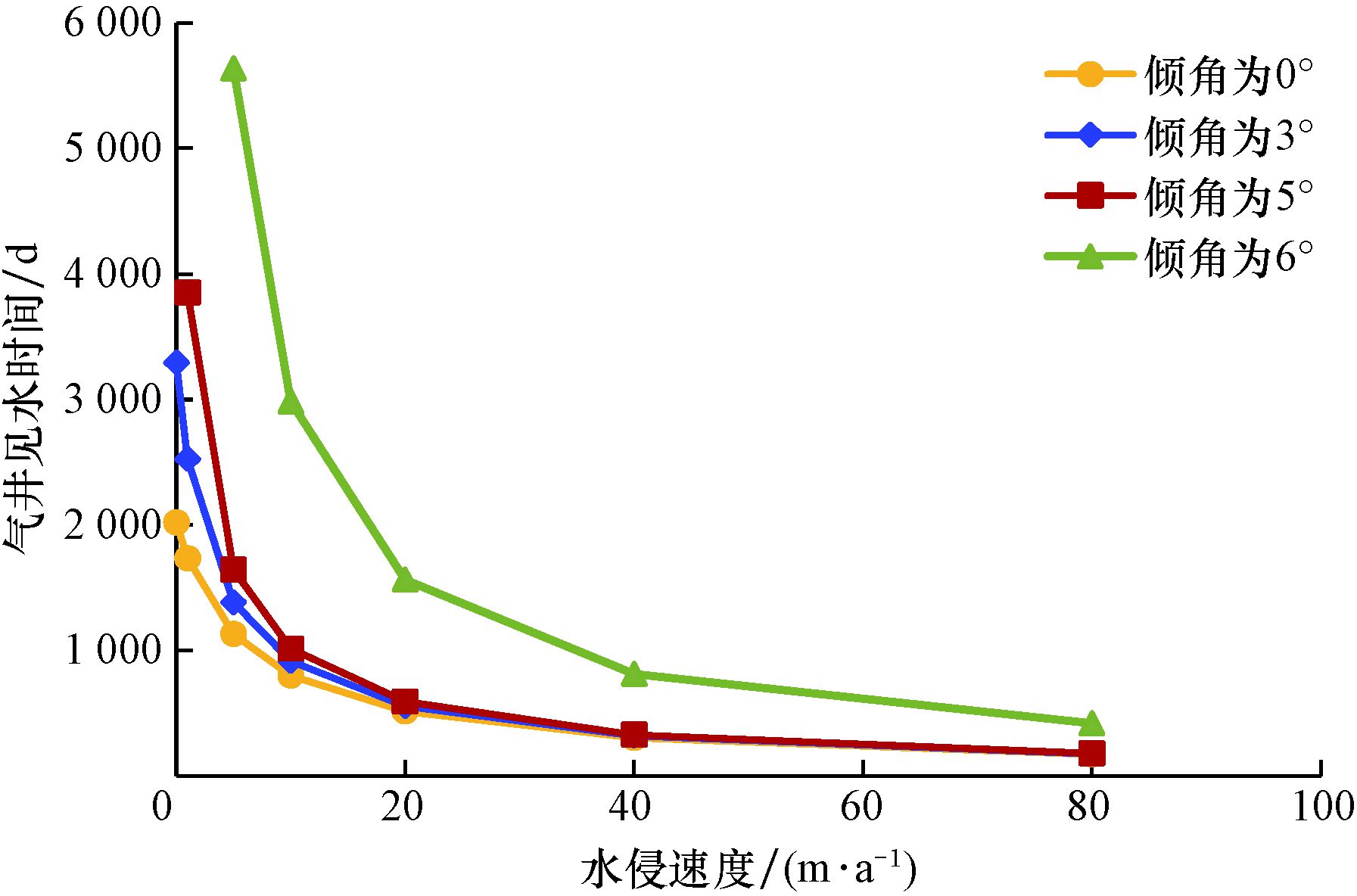
图 6为不同储层倾角下气井见水时间与水侵速度的关系。
|
| 图 6 不同储层倾角下的气井见水时间与水侵速度的关系 Fig.6 Relationship of water breakthrough timing vs. water invastion speed at different reservoir dip |
由图 6可知,随着水侵速度增大,气井见水时间短缩。当水侵速度小于20 m/a时,随着水侵速度增大,气井见水时间急剧缩短;当水侵速度大于20 m/a且储层倾角小于5°时,气井见水时间相差不大。分析认为,当储层倾角小于5°时,重力作用不显著,在较大水侵速度和驱动压力作用下,水质点迅速舌进至井筒;当储层倾角大于5°时,重力作用显著,远离井眼位置的驱动压力小于重力,水的运移主要靠水侵,故使气井见水时间增长。
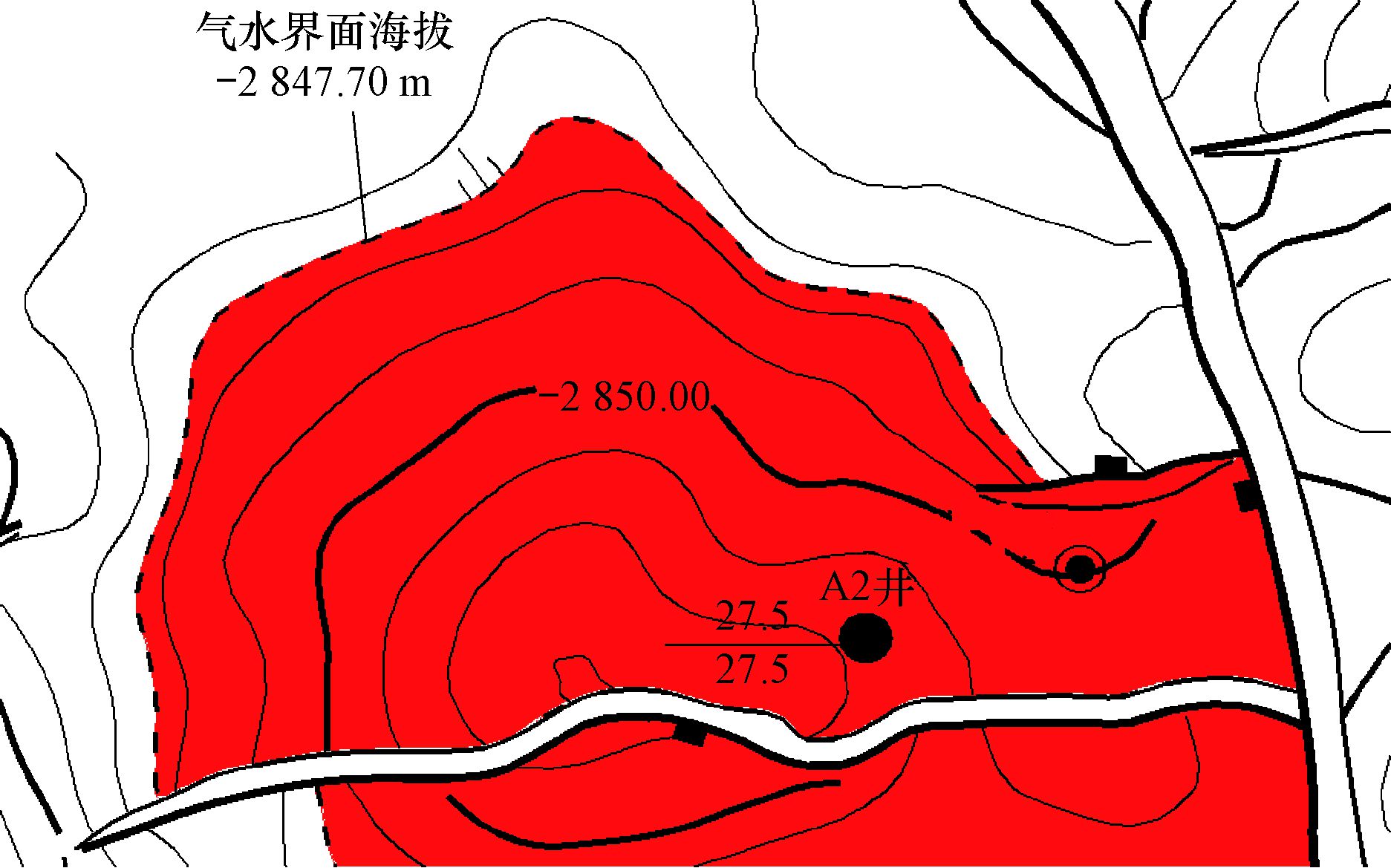
3 实例分析以某断块背斜边水气藏为例,分析储层倾角和水侵对气藏见水时间的影响。该断块南部和东部均有一条断层,水体主要存在于西部,A2井 (开发井) 处于构造高点,井点海拔-2 830.20 m,气水界面海拔-2 874.70 m,储层倾角约4°,气柱高度为27.50 m。A2井的含气区域如图 7所示。该井其他储层参数为:地层压力pR=30.4 MPa,孔隙度φ=0.12,绝对渗透率Ke=200 mD,体积系数Bg=0.035,气相黏度μg=0.024 mPa·s,水相黏度μw=0.240 mPa·s,储层有效厚度h=27.5 m;残余气饱和度Sgr=0.35;原始地层水饱和度Swi=0.41;残余气对应水相相对渗透率Kwgr=0.31;原始水对应气相相对渗透率Kgwi=0.58。
|
| 图 7 A2井含气区域示意 Fig.7 The gas bearing area of Well A2 |
该井于2010年4月18日投产,产气量10×104 m3/d,其水气比和氯根浓度变化如图 8所示。
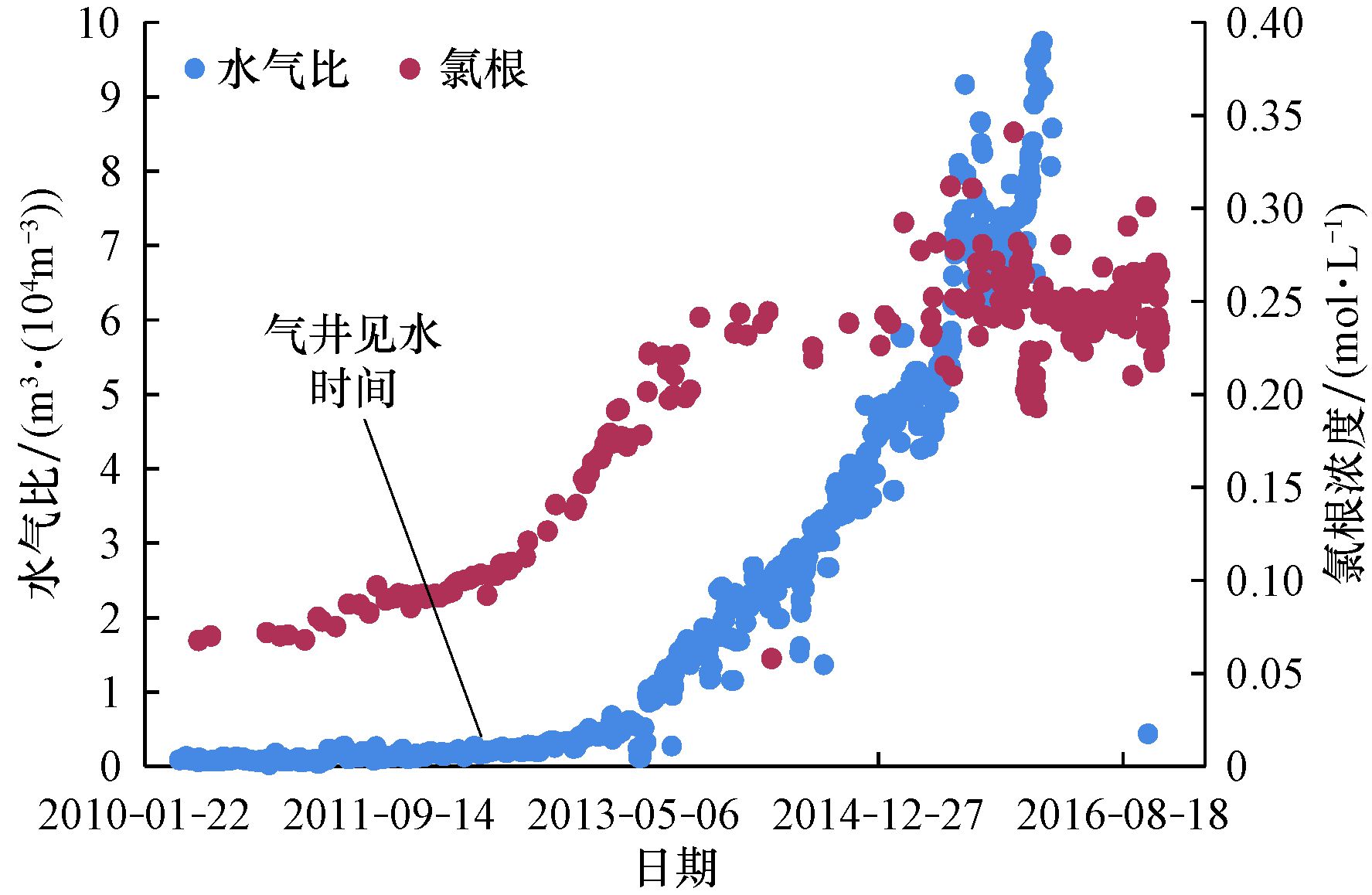
|
| 图 8 A2井水气比和氯根浓度变化 Fig.8 Chloride concentration and water/gas ratio of Well A2 |
从图 8可以看出,该井生产初期氯根浓度在0.07 mol/L左右,而后氯根浓度逐渐增大,于2012年9月27日急剧增大至0.20 mol/L,水气比陡增至1.0 m3/104m3以上,表明边水已经侵入到井底,至此气井已生产870 d左右,根据物质平衡方程得到该井水侵速度约为10 m/a。结合该井储层参数,利用式 (17) 计算不考虑倾角和水侵影响的见水时间为2 042 d,综合式 (4)、式 (18)、式 (19) 和式 (20) 得到考虑储层倾角和水侵影响的见水时间为880 d。可见,考虑储层倾角和水侵影响预测的见水时间与实际情况更相符。
4 结论1) 基于物质平衡方程及多孔介质流体渗流理论,考虑储层倾角及水侵的影响,以质点流动驱动力和沿倾角方向的重力为依据,将储层水的运移分为水侵阶段和舌进阶段,建立了带倾角边水气藏见水时间预测模型。
2) 储层倾角及水侵对见水时间的影响研究结果表明,舌进时间随储层倾角增大先增长后缩短,两者之间呈复杂非线性关系,水侵速度与水侵时间呈反比。当储层倾角较小时,水侵距离小于舌进距离,水运移主要靠舌进,在驱动压力和水侵影响下,气井见水时间缩短;随着储层倾角逐渐增大,水侵距离逐渐增大,舌进距离逐渐缩短,远离井的储层位置质点的驱动压力小于重力,水的运移靠水侵,水侵速度一般小于水舌进速度,从而导致见水时间增长;水侵速度越大,见水越早,水侵速度较小时,见水时间对水侵速度比较敏感,且随水侵速度增大,见水时间对水侵速度的敏感性减弱。
3) 在其他因素都相同的情况下,考虑储层倾角及水侵影响预测的带倾角边水气藏见水时间与常规不考虑储层倾角及水侵影响的相比,更符合储层流体的渗流情况,预测的见水时间更接近实际生产情况,可为现场及时采取防水措施提供依据。
| [1] | MUSKAT M, WYCOKOFF R D. An approximate theory of water-coning in oil production[J]. Transactions of the AIME, 1935, 114 (1) : 144–163. DOI:10.2118/935144-G |
| [2] | MEYER H I, GARDER A O. Mechanics of two immiscible fluids in porous media[J]. Journal of Applied Physics, 1954, 25 (11) : 1400–1406. DOI:10.1063/1.1721576 |
| [3] | KARP J C, LOWE D K, MARUSOV N. Horizontal barriers for controlling water coning[J]. Journal of Petroleum Technology, 1962, 14 (7) : 783–790. DOI:10.2118/153-PA |
| [4] | SOBOCINSKI D P, CORNELIUS A J. A correlation for predicting water coning time[J]. Journal of Petroleum Technology, 1965, 17 (5) : 594–600. DOI:10.2118/894-PA |
| [5] | WHEATLEY M J.An approximate theory of oil/water coning[R].SPE 14210, 1985. |
| [6] | HØYLAND L A, PAPATZACOS P, SKJAEVELAND S M. Critical rate for water coning:correlation and analytical solution[J]. SPE Reservoir Engineering, 1989, 4 (4) : 495–502. DOI:10.2118/15855-PA |
| [7] | GUO B Y, LEE R L-H. A simple approach to optimization of completion interval in oil/water coning systems[J]. SPE Reservoir Engineering, 1993, 8 (4) : 249–255. DOI:10.2118/23994-PA |
| [8] |
程林松, 郎兆新, 张丽华.
底水驱油藏水平井锥进的油藏工程研究[J]. 石油大学学报 (自然科学版), 1994, 18 (4) : 43–47.
CHENG Linsong, LANG Zhaoxin, ZHANG Lihua. Reservoir engineering problem of horizontal wells coning in bottom water drive reservoir[J]. Journal of Petroleum University, China (Edition of Science & Technology), 1994, 18 (4) : 43–47. |
| [9] |
张烈辉, 严谨, 李允, 等.
考虑凝析油析出时的底水凝析气藏见水时间预测新方法[J]. 天然气工业, 2004, 24 (7) : 74–75.
ZHANG Liehui, YAN Jin, LI Yun, et al. New method to predict condensing effect on water breakthrough in condensate reservoirs with bottom water[J]. Natural Gas Industry, 2004, 24 (7) : 74–75. |
| [10] |
王会强, 李晓平, 吴锋, 等.
边水气藏气井见水时间预测方法[J]. 特种油气藏, 2008, 15 (4) : 73–74.
WANG Huiqiang, LI Xiaoping, WU Feng, et al. Prediction of water breakthrough time in gas reservoirs with edge water[J]. Special Oil & Gas Reservoirs, 2008, 15 (4) : 73–74. |
| [11] |
吴克柳, 李相方, 张公涛, 等.
考虑反凝析的边水凝析气藏见水时间预测新方法[J]. 科学技术与工程, 2011, 11 (19) : 4574–4577.
WU Keliu, LI Xiangfang, ZHANG Gongtao, et al. A novel approach to predict water breakthrough time in gas condensate reservoir with edge water considering retrograde condensation[J]. Science Technology and Engineering, 2011, 11 (19) : 4574–4577. |
| [12] |
张庆辉, 屈信忠, 柳金城, 等.
低渗透底水气藏压裂气井见水时间预测[J]. 新疆石油地质, 2014, 35 (1) : 77–81.
ZHANG Qinghui, QU Xinzhong, LIU Jincheng, et al. Prediction of water breakthrough time in fractured gas well in low-permeability gas reservoir with bottom water[J]. Xinjiang Petroleum Geology, 2014, 35 (1) : 77–81. |
| [13] |
李志军, 戚志林, 宿亚仙, 等.
基于水侵预警的边水气藏动态预测模型[J]. 西南石油大学学报 (自然科学版), 2014, 36 (3) : 87–92.
LI Zhijun, QI Zhilin, SU Yaxian, et al. Dynamic prediction model of edge-water gas reservoir based on water invasion early warning[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014, 36 (3) : 87–92. |
| [14] |
李涛, 袁舟, 陈伟, 等.
气藏水平井边水突破时间预测[J]. 断块油气田, 2014, 21 (3) : 341–343.
LI Tao, YUAN Zhou, CHEN Wei, et al. Prediction on water breakthrough time of horizontal well in gas reservoir with edge water[J]. Fault-Block Oil & Gas Field, 2014, 21 (3) : 341–343. |
| [15] |
张庆辉, 李相方, 张磊, 等.
考虑启动压力梯度的低渗底水气藏见水时间预测[J]. 石油钻探技术, 2012, 40 (5) : 96–99.
ZHANG Qinghui, LI Xiangfang, ZHANG Lei, et al. Prediction of water breakthrough time in low permeability gas reservoirs with bottom water in consideration of threshold pressure[J]. Petroleum Drilling Techniques, 2012, 40 (5) : 96–99. |
| [16] |
汪周华, 王子敦, 邓丹, 等.
考虑重力及气体非达西效应影响的边水气藏边水突破时间预测模型[J]. 石油钻采工艺, 2016, 38 (2) : 210–215.
WANG Zhouhua, Wang Zidun, DENG Dan, et al. Model for prediction of edge-water breakthrough time in reservoirs with edge water with consideration to effects of gravity and non-Darcy effect of gass[J]. Oil Drilling & Production Technology, 2016, 38 (2) : 210–215. |




