准噶尔盆地玛东油田水平井高性能油基钻井液技术

张雄; 余进; 毛俊; 刘祖磊

doi:10.11911/syztjs.2020106

准噶尔盆地玛东油田水平井高性能油基钻井液技术

中国石油集团西部钻探工程有限公司钻井液分公司，新疆克拉玛依 834000

详细信息

作者简介:
张雄（1979—），男，湖北黄梅人，2003年毕业于江汉石油学院化学工程与工艺专业，高级政工师，主要从事项目管理工作。E-mail：89227198@qq.com

中图分类号: TE254⁺.3
计量
- 文章访问数: 752
- HTML全文浏览量: 261
- PDF下载量: 102
出版历程
- 收稿日期: 2020-03-06
- 修回日期: 2020-08-04
- 网络出版日期: 2020-09-08
- 刊出日期: 2020-11-30

High-Performance Oil-Based Drilling Fluid Technology for Horizontal Wells in the Madong Oilfield, Junggar Basin

Drilling Fluid Company, PetroChina Xibu Drilling Engineering Company Limited, Karamay, Xinjiang, 834000, China

摘要

摘要: 准噶尔盆地玛东油田水平井造斜段和水平段存在因泥岩水化、压力异常和砂砾层多而造成的起下钻阻卡、井眼失稳和机械钻速低等问题，为此开展了高性能油基钻井液技术研究。根据玛东油田的储层特征和中长水平段的钻进要求，配制了XZ高性能油基钻井液，并通过室内试验评价了其加重、抗高温、提切、封堵承压、抗污染和抗冻等性能。试验结果显示：该油基钻井液密度在1.35～2.01 kg/L时流变性能稳定、切力可调；热、冻稳定性好，低温可至–24 ℃，高温可达180 ℃；乳化稳定性好，破乳电压普遍在1 000 V以上；抗污染能力强，可抗20%钻屑、20%地层水和10%水泥的污染；封堵能力强，分别采用孔径为120和150 μm的砂盘进行承压封堵时，承压均可达15 MPa。该钻井液在玛东油田4口井进行了应用，钻井过程中井眼稳定，造斜段井径扩大率仅3.55%，起下钻顺利，平均机械钻速较同层位水基钻井液提高79%，取得了显著的提速效果。研究结果表明，采用XZ高性能油基钻井液可以解决玛东油田砂砾岩储层水平井钻井中存在的问题，满足该油田长水平段安全快速钻井需求。
- 水平井 /
- 油基钻井液 /
- 钻井液性能 /
- 井眼稳定 /
- 机械钻速 /
- 玛东油田 /
- 准噶尔盆地
Abstract: The build-up section and horizontal section drilling in horizontal wells of the Madong Oilfield, Junggar Basin was challenged by problems such as pipe-string sticking during trip operations, wellbore instability, and low ROP caused by the hydration of mudstone, abnormal pressure, and an abundance of glutenites. Therefore, high-performance oil-based drilling fluid was accordingly investigated. Based on the reservoir characteristics of the Madong Oilfield and the drilling requirements of the medium-long horizontal sections, XZ high-performance oil-based drilling fluid was hereby formulated, and indoor laboratory experiments were carried out to evaluate its weighting, temperature resistance, shear strength improving, sealing/pressure-bearing, anti-pollution and anti-freezing performances. The results showed that this oil-based drilling fluid system exhibited stable rheological properties and an adjustable shear force between the density of 1.35–2.01 kg/L. The new fluid exhibited good thermal and freezing stability, low temperature resistance of up to –24 ℃, and high temperature resistance of up to 180 ℃. The emulsification stability was good, and the demulsification voltage was generally above 1 000 V. The anti-pollution ability was strong, the anti-cuttings pollution concentration was ≥20.0%, the anti-formation water pollution concentration was ≥20.0%, and the anti-cement pollution concentration was ≥10.0%. Further, the new drilling fluid system had strong sealing ability. When using sand discs with a diameter of 120 and 150 μm for pressure-bearing sealing, the pressure-resistance of both discs could reach 15 MPa. This system was applied in 4 of the wells in the Madong Oilfield. After the application of the new fluid, perfect borehole stability was achieved, the hole enlargement rate of the build-up section was only 3.55%, the trip operation was completed smoothly, and the average ROP was 79.0% higher than that of the same horizon drilled with water-based drilling fluid. A remarkable drilling speed-up effect was observed. The research results showed that the application of XZ high-performance oil-based drilling fluid can solve the technical problems in the development of the glutenite reservoirs in the Madong Oilfield and satisfy the needs of safe and fast drilling in the long horizontal section of this oilfield.
- horizontal well /
- oil-based drilling fluid /
- drilling fluid property /
- hole stabilization /
- penetration rate /
- Madong Oilfield /
- Junggar Basin

HTML全文

与陆上和浅海钻井相比，深水钻井普遍面临着地层安全密度窗口较窄的问题^[1-5]。为了解决深水窄密度窗口安全钻井问题，李军等人^[6-8]提出了基于井下分离的新型双梯度钻井技术，设计了新型井下旋流分离器，并开展了室内循环分离试验，验证了分离器的有效性和井筒内双压力梯度的可行性。

深水钻井过程中气侵溢流频发，给钻井作业带来了极大的井控安全挑战^[9]。明确气侵后气体在井筒中的运移行为，并掌握相关参数的变化规律，对早期溢流监测和井筒压力控制具有重要作用。对于基于井下分离的新型双梯度钻井而言，分离器的存在使环空内不再是单一密度的流体，而是2种密度的流体共存，因此在分离器处存在液相密度突变的现象。然而，现有的气液两相流模型未考虑液相密度突变对气体运移的影响^[10-11]，不适用于新型双梯度钻井的气侵模拟。为此，笔者基于井筒气液两相流理论，考虑井筒内液相密度突变对气体运移的影响，建立了适用于新型双梯度钻井的井筒气液两相流模型，分析了气侵条件下环空出口流量的变化，并探讨了不同因素变化对环空出口流量变化率的影响，为气侵条件下新型双梯度钻井环空出口流量预测和早期溢流监测提供了理论依据。

1. 气液两相流模型的建立

1.1 物理模型

新型双梯度钻井循环过程中，分离器上部环空为低密度钻井液，下部环空为高密度钻井液（见图1）。气侵发生后，气体从井底向井口运移过程中液相密度会产生突变，从而对井筒流动参数产生显著影响。因此，建立井筒气液两相流模型时，必须考虑液相密度突变对气体运移的影响。

图 1 新型双梯度钻井井筒物理模型

Figure 1. A new physical model of the wellbore in dual-gradientdrilling

下载: 全尺寸图片幻灯片

1.2 气液两相流数学模型

1.2.1 质量守恒方程

气相质量守恒方程为：

$\frac{\partial }{{\partial z}}({\rho _{\rm{g}}}{\alpha _{\rm{g}}}{v_{\rm{g}}}A) + \frac{\partial }{{\partial t}}({\rho _{\rm{g}}}{\alpha _{\rm{g}}}A) = {q_{\rm{g}}}$

(1)

液相质量守恒方程为：

$\frac{\partial }{{\partial z}}({\rho _{\rm{l}}}{\alpha _{\rm{l}}}{v_{\rm{l}}}A) + \frac{\partial }{{\partial t}}({\rho _{\rm{l}}}{\alpha _{\rm{l}}}A) = 0$

(2)

式中：t为时间，s；z为轴向位移，m；A为环空流道面积，m²；ρ_g和ρ_l分别为气相和钻井液的密度，kg/m³；α_g和α_l分别为气相和钻井液的体积分数；v_g和v_l分别为气相和钻井液的实际流速，m/s；q_g为单位高度气体侵入速度，kg/(s·m)。

1.2.2 动量守恒方程

气液两相动量守恒方程为：

$\begin{array}{l} \dfrac{\partial }{{\partial z}}({\rho _{\rm{g}}}{\alpha _{\rm{g}}}{v_{\rm{g}}}^2A + {\rho _{\rm{l}}}{\alpha _{\rm{l}}}{v_{\rm{l}}}^2A) + \dfrac{\partial }{{\partial t}}({\rho _{\rm{g}}}{\alpha _{\rm{g}}A}{v_{\rm{g}}} + {\rho _{\rm{l}}}{\alpha _{\rm{l}}}{v_{\rm{l}}}A) + \\ ({\rho _{\rm{g}}}{\alpha _{\rm{g}}} + {\rho _{\rm{l}}}{\alpha _{\rm{l}}})gA\sin \theta + \dfrac{\partial }{{\partial z}}(pA) + A\dfrac{{\partial {p_{\rm{f}}}}}{{\partial z}} = 0 \\[-13pt] \end{array}$

(3)

式中：p为压力，Pa；g为重力加速度，m/s²；θ为井眼方向与水平方向的夹角，（°）；p_f为流动压耗，Pa。

井筒温度采用新型双梯度钻井正常循环时的温度场模型进行计算，具体计算方法见文献[12]。

1.3 辅助方程

1.3.1 漂移流模型

采用N. Zuber等人^[13]提出的考虑气液相间滑脱效应的漂移流模型，气液两相流可分为泡状流、分散泡状流、段塞流、搅动流和环状流等5种流型。流型判别方法及不同流型条件下的参数计算方法见文献[14]。

1.3.2 摩阻压降模型

摩阻压降计算公式为：

$\frac{{\partial {p_{\rm{f}}}}}{{\partial z}}{\rm{ = }}\frac{{2f{\rho _{\rm{m}}}{v_{\rm{m}}}^2}}{{{D_{\rm{i}}} - {D_{\rm{p}}}}}$

(4)

$\!{\text{其中}}\qquad\qquad\qquad {\rho _{\rm{m}}} = {\rho _{\rm{l}}}{\alpha _{\rm{l}}} + {\rho _{\rm{g}}}{\alpha _{\rm{g}}}\qquad$

(5)

${v_{\rm{m}}} = {v_{{\rm{sl}}}} + {v_{{\rm{sg}}}} = {v_{\rm{l}}}{\alpha _{\rm{l}}} + {v_{\rm{g}}}{\alpha _{\rm{g}}}$

(6)

式中：ρ_m为气液两相混合物密度，kg/m³；v_m为气液两相混合物的流速，m/s；v_sg和v_sl分别为气相和液相的表观速度，m/s；D_i为环空外径，m；D_p为环空内径，m。

1.3.3 环空流体密度分布

与常规单梯度钻井不同，分离器的存在使新型双梯度钻井井筒内同时存在2种密度的流体，且流体密度分布与分离器位置密切相关。密度分布方程为：

${\rho _{\rm{l}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {{\rho_{\rm{a}}}\begin{array}{*{20}{c}} {}&{h \leqslant H - {L_{{\rm{bs}}}}} \end{array}} \\ {{\rho_{\rm{b}}}\begin{array}{*{20}{c}} {}&{h > H - {L_{{\rm{bs}}}}} \end{array}} \end{array}} \right.$

(7)

式中：ρ_a为低密度钻井液密度，kg/m³；ρ_b为高密度钻井液密度，kg/m³；H为总井深，m；h为井筒任意点深度，m；L_bs为分离器与钻头间距，m。

由式（7）可知，气侵发生后，气体从地层进入井筒后先侵入高密度钻井液并在其中运移，气体从井底向上运移过程中前沿到达分离器时，由于环空流体密度发生了突变，此后气体前沿进入低密度钻井液中并运移至井口。分离器位置处环空流体密度突变对气体运移产生显著影响，使气侵后新型双梯度钻井的井筒流体流动参数的变化规律与常规单梯度钻井时有明显差异。

1.3.4 气体前沿位置及气侵量确定方法

采用界面追踪法确定气体前沿位置，根据气体状态方程和密度方程确定不同温度压力条件下的气相质量流量，具体计算方法见文献[14]。此外，钻遇气藏时，若井底压力小于地层压力，地层气体将侵入井筒环空；由于气体侵入过程符合非达西渗流，因此采用二项式定理计算井底气侵量，具体计算方法见文献[15]。

2. 模型求解

2.1 初始边界条件

气侵初始时刻，井筒环空内只有井底边界有气体，结合钻井液稳定流动模型可以确定初始时刻环空各点的压力，以及钻井液和气体各组分的体积分数和速度。

$p(z,0) = p(z)$

(8)

$\left\{ {\begin{array}{*{20}{c}} {{\alpha _{\rm{g}}}(H,0) = \dfrac{{{v_{{\rm{sg}}}}(H,0)}}{{{c_0}{v_{\rm{m}}} + {v_{{\rm{gr}}}}}}} \\ {{\alpha _{\rm{g}}}(0 \sim H - 1,0) = 0} \end{array}} \right.$

(9)

${\alpha _{\rm{l}}}(z,0) = 1 - {\alpha _{\rm{g}}}(z,0)$

(10)

$\left\{ {\begin{array}{*{20}{c}} {{v_{\rm{g}}}(H,0) = \dfrac{{{v_{\rm{sg}}}}(H,0)}{{{\alpha _{\rm{g}}}(H,0)}}} \\ {{v_{\rm{g}}}(0 \sim H - 1,0) = 0} \end{array}} \right.$

(11)

${v_{\rm{l}}}(z,0) = \frac{{{v_{{\rm{sl}}}}(z,0)}}{{{\alpha _{\rm{l}}}(z,0)}}$

(12)

式中：c₀为气相分布系数；v_gr为气相滑脱速度，m/s。

整个钻井过程中，井口回压维持不变，作为井筒压力边界条件。

$p(0,t) = {p_{{\rm{bp}}}}$

(13)

式中：p_bp为井口回压，Pa。

2.2 模型离散结果

采用一阶迎风差分格式对控制方程中的空间导数项进行离散差分，采用四点中心差分格式对时间导数项进行离散差分。对气液两相流动过程中的井筒压力模型进行离散化，给出相应的有限差分格式。

气相质量守恒方程为：

$\begin{split} & \qquad\qquad\;\;({\rho _{\rm{g}}}{\alpha _{\rm{g}}}{v_{\rm{g}}})_i^n - x({\rho _{\rm{g}}}{\alpha _{\rm{g}}}{v_{\rm{g}}})_{i - 1}^n = \\ & \dfrac{{\Delta z}}{{2\Delta t}}[x({\rho _{\rm{g}}}{\alpha _{\rm{g}}})_{i - 1}^{n - 1} + ({\rho _{\rm{g}}}{\alpha _{\rm{g}}})_i^{n - 1} - x({\rho _{\rm{g}}}{\alpha _{\rm{g}}})_{i - 1}^n -\\ &\qquad\; ({\rho _{\rm{g}}}{\alpha _{\rm{g}}})_i^n] + \dfrac{{\Delta z}}{{2{A_i}}}[({q_{\rm{g}}})_{i - 1}^n + ({q_{\rm{g}}})_i^n] \end{split}$

(14)

式中：i和n分别代表轴向节点和时间节点。

液相质量守恒方程为：

$\begin{split} & \qquad\qquad ({\rho _{\rm{l}}}{\alpha _{\rm{l}}}{v_{\rm{l}}})_i^n - x({\rho _{\rm{l}}}{\alpha _{\rm{l}}}{v_{\rm{l}}})_{i - 1}^n =\\ &\!\!\!\!\!\!\!\!\!\! \dfrac{{\Delta z}}{{2\Delta t}}[x({\rho _{\rm{l}}}{\alpha _{\rm{l}}})_{i - 1}^{n - 1} + ({\rho _{\rm{l}}}{\alpha _{\rm{l}}})_i^{n - 1} - x({\rho _{\rm{l}}}{\alpha _{\rm{l}}})_{i - 1}^n - ({\rho _{\rm{l}}}{\alpha _{\rm{l}}})_i^n]\!\!\! \end{split}$

(15)

动量守恒方程：

$\begin{split} & \qquad\qquad\qquad p_i^n - xp_{i - 1}^n = \\ & \!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \dfrac{{\Delta z}}{{2\Delta t}}(xV_{1_{i - 1}^{n - 1}} + V_{1_i^{n - 1}} - xV_{1_{i - 1}^n} - V_{1_i^n}) + xV_{2_{i - 1}^n} - V_{2_i^n} - \\ &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \dfrac{{g\Delta z}}{2}(xV_{3_{i - 1}^n} + V_{3_i^n}) - \dfrac{{\Delta z}}{2}\left[\left(x\dfrac{{\partial {p_{\rm{f}}}}}{{\partial z}}\right)_{i - 1}^n + \left(\dfrac{{\partial {p_{\rm{f}}}}}{{\partial z}}\right)_i^n\right] \end{split} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$

(16)

$\!{\text{其中}}\quad\;\;\qquad\qquad\qquad x = \frac{{{A_{i - 1}}}}{{{A_i}}}\qquad$

(17)

$V_1 = {\rho _{\rm{g}}}{\alpha _{\rm{g}}}{v_{\rm{g}}} + {\rho _{\rm{l}}}{\alpha _{\rm{l}}}{v_{\rm{l}}}$

(18)

$V_2 = {\rho _{\rm{g}}}{\alpha _{\rm{g}}}{v_{\rm{g}}}^2 + {\rho _{\rm{l}}}{\alpha _{\rm{l}}}{v_{\rm{l}}}^{\rm{2}}$

(19)

$V_3 = {\rho _{\rm{g}}}{\alpha _{\rm{g}}} + {\rho _{\rm{l}}}{\alpha _{\rm{l}}}$

(20)

2.3 求解步骤

采用迭代方法对气液两相流动模型进行求解，具体计算步骤为：1）针对井筒系统划分网格，输入初始边界条件；2）假设n+1时刻的井底压力为 $p_{\rm{H}}^{n + 1}$ ，确定井底气侵量、各相体积分数和流速；3）假设节点i处n+1时刻的压力为 $p_i^{n + 1(0)}$ ，由状态方程确定各相的物性参数；4）假设节点i处n+1时刻的气相体积分数为 $\alpha _i^{n + 1(0)}$ ，根据质量守恒方程预估相表观流速，并结合漂移流模型求解新的气相体积分数 $\alpha _i^{n + 1}$ ；5）判断计算得到的气相体积分数是否满足精度要求，不满足时返回步骤4）进行校正计算，直至满足精度要求；6）计算得到钻井液的体积分数，同时结合动量守恒方程，计算出新节点i处的压力 $p_i^{n + 1}$ ，然后判断是否满足精度要求，即 $\left| {p_i^{n + 1} - p_i^{n + 1(0)}} \right| < \varepsilon$ ，不满足时返回步骤3）进行校正计算，直至精度满足要求；7）节点循环到环空井口，若井口回压满足 $\left| {p_{{\rm{bp}}}^{n + 1} - {p_{{\rm{bp}}}}} \right| < \varepsilon$ ，说明n+1时刻的井筒压力场估算正确，否则返回步骤2）进行校正计算，直至满足要求；8）n+1时刻计算完毕，迭代计算下一时刻。

3. 气侵条件下环空出口流量的影响因素分析

进行新型双梯度钻井时，环空出口流量是深水钻井监测溢流的重要指标，可通过流量计实时测量。通过数值模拟，分析了气侵条件下环空出口流量的变化，并探讨了不同因素变化对环空出口流量变化率的影响。模拟井的基本参数为：井深4 000 m，水深1 500 m，套管鞋深度3 000 m，隔水管内径482.6 mm，套管内径244.5 mm，钻杆外径127.0 mm，钻杆内径101.6 mm，钻头直径215.9 mm，分离器与钻头间距500 m，低密度钻井液密度0.9 kg/L、黏度4 mPa·s，高密度钻井液密度1.1 kg/L、黏度6 mPa·s，钻井液排量20 L/s，气侵量0.40 m³/s，井口回压0.5 MPa。

3.1 井深

在其他条件不变的情况下，井深分别为3 200，3 600和4 000 m时，由于分离器与钻头间距始终为500 m，此时3种井深条件下对应的分离器位置分别为井深2 700，3 100和3 500 m，分别模拟了3种井深条件下气侵发生后，环空出口流量变化率随气体前沿位置的变化情况，结果见图2。从图2可以看出，3种井深条件下气体前沿到达分离器时的环空出口流量变化率均发生突增。此外，由于气侵量相同，3种井深条件下的环空流量变化幅度非常接近，环空流量变化率分别突增至30.1%，29.1%和28.4%。此外，3种井深条件下气体前沿到达分离器所需要的时间分别为7.8，6.5和6.6 min，气体前沿到达隔水管底端所需要的时间分别为25.0，29.0和34.0 min。

图 2 不同井深条件下环空出口流量变化率与气体前沿位置的关系

Figure 2. Relationship between the change rate of annular outlet flow rate and gas front position at different well depths

下载: 全尺寸图片幻灯片

分析认为，发生突增现象的原因是：当气体前沿到达分离器时，分离器的存在使液相密度由高变低，气体进入低密度液体时气液两相间的气体滑脱速度和气体流速突然增大，且低压环境使气体向上流动过程中更容易膨胀，加速了气侵的进一步发展，使环空出口流速突然加快，从而导致环空出口流量变化率发生突增。

3.2 气侵量

在其他条件不变的情况下，分别模拟了气侵量分别为0.05，0.20和0.40 m³/s时，环空出口流量变化率随气体前沿位置的变化情况，结果见图3。从图3可以看出，环空出口流量变化率均在气体前沿到达分离器所在位置（井深3 500 m）时发生突增；随着气侵量增大，环空流量变化幅度也随之增大，3种气侵量条件下的环空流量变化率分别突增至23.0%，25.3%和28.4%。此外，3种气侵量条件下气体前沿到达分离器所需要的时间分别为6.9，6.8和6.6 min，气体前沿到达隔水管底端所需要的时间分别为36.0，35.0和34.0 min。

图 3 不同气侵量条件下环空出口流量变化率与气体前沿位置的关系

Figure 3. The relationship between the change rate of annular outlet flow and gas front position under different gas cut conditions

下载: 全尺寸图片幻灯片

3.3 分离器位置

在其他条件不变的情况下，分离器与钻头间距分别为500，1 000和1 500 m时，对应的分离器位置分别在井深3 500，3 000和2 500 m，分别模拟了3种分离器位置条件下气侵发生后环空出口流量变化率随气体前沿位置的变化情况，结果见图4。从图4可以看出，气体前沿到达分离器所在位置（井深3 500，3 000 m和2 500 m）时环空出口流量变化率均发生突增，3种分离器位置条件下的环空流量变化率分别突增至28.4%，29.6%和30.4%；分离器与钻头间距越小，环空出口流量变化率发生突增的时间越早。这是因为，分离器与钻头间距越小，气侵发生后气体前沿到达分离器所在位置的时间越早，因此环空出口流量变化率发生突增的时间越早。3种分离器位置条件下气体前沿到达分离器所在位置需要的时间分别为6.6，13.1和21.8 min，气体前沿到达隔水管底端所需要的时间分别为34.0，35.0和36.0 min。

图 4 不同分离器位置条件下环空出口流量变化率与气体前沿位置的关系

Figure 4. The relationship between change rate of annular outlet flow and gas front position under different separator conditions

下载: 全尺寸图片幻灯片

3.4 低密度/高密度钻井液密度差

在其他条件不变的情况下，模拟时设定分离器下部高密度钻井液的密度恒定为1.1 kg/L，钻井液密度差分别为0.1，0.2和0.3 kg/L时，对应分离器上部低密度钻井液密度分别为1.0，0.9和0.8 kg/L，分别模拟了3种低密度/高密度钻井液密度差条件下发生气侵后，环空出口流量变化率随气体前沿位置的变化情况，结果见图5。从图5可以看出，3种低密度/高密度钻井液密度差条件下，环空出口流量变化率均在气体前沿到达分离器（井深3 500 m）时发生突增；随着流体密度差增大，环空流量变化幅度也随之明显增大，3种低密度/高密度钻井液密度差条件下的环空流量变化率分别突增至15.8%，28.4%和44.1%。此外，3种低密度/高密度钻井液密度差条件下气体前沿到达分离器所在位置需要的时间分别为6.6，6.6和6.5 min，气体前沿到达隔水管底端所需要的时间分别为36.0，34.0和31.0 min。

图 5 不同低密度/高密度钻井液密度差条件下环空出口流量变化率与气体前沿位置的关系

Figure 5. The relationship between change rate of an annular outlet flow and gas front position under different density differences of low/high density drilling fluids

下载: 全尺寸图片幻灯片

3.5 排量

在其他条件不变的情况下，分别模拟了3种排量条件下发生气侵后，环空出口流量变化率随气体前沿位置的变化情况，结果见图6。从图6可以看出，3种排量条件下的环空出口流量变化率均在气体前沿到达分离器所在位置（井深3 500 m）时发生突增；随着排量增大，环空出口流量变化幅度随之减小。3种排量条件下的环空出口流量变化率分别突增至28.4%，26.1%和25.0%。此外，排量越大，环空出口流量变化率发生突增的时间越早。这是因为，排量越大，气侵发生后气体运移速度越大，气体前沿到达分离器所在位置的时间越早，因此环空出口流量变化率发生突增的时间越早。3种排量条件下气体前沿到达分离器所在位置需要的时间分别为6.6，4.7和3.7 min，气体前沿到达隔水管底端所需要的时间分别为34.0，25.0和19.0 min。

图 6 不同排量条件下环空出口流量变化率与气体前沿位置的关系

Figure 6. The relationship between the change rate of an annular outlet flow and gas front position under different pumping rates

下载: 全尺寸图片幻灯片

3.6 井口回压

在其他条件不变的情况下，分别模拟了3种井口回压条件下发生气侵后，环空出口流量变化率随气体前沿位置的变化情况，结果见图7。从图7可以看出，3种井口回压条件下的环空流量变化率均在气体前沿到达分离器所在位置（井深3 500 m）时发生突增；井口回压对环空出口流量变化率的影响不大，3种井口回压条件下环空流量变化率均突增至28.4%。3种井口回压条件下气体前沿到达分离器所在位置需要的时间均为6.6 min，气体前沿到达隔水管底端所需要的时间均为34.0 min。

图 7 不同井口回压条件下环空出口流量变化率与气体前沿位置的关系

Figure 7. The relationship between the change rate of annular outlet flow and gas front position under different wellhead backpressures

下载: 全尺寸图片幻灯片

以上研究表明：1）气体前沿到达分离器时，不同参数范围条件下环空出口流量变化率均发生明显突增，说明环空出口流量的可监测性较强；2）分离器位于泥线以下时，环空出口流量发生突增的时间要早于隔水管底端见气时间。因此，与监测隔水管底端含气率的方法相比，通过监测环空出口流量的突增现象可以更早地发现气侵。

4. 环空出口流量变化率影响因素敏感性分析

在研究气侵条件下不同因素对新型双梯度钻井环空出口流量变化规律影响的基础上，分析突增后环空出口流量变化率的敏感性，但不同影响因素之间量纲不一致，无法简单统一和对比分析。因此，引入比变异系数，用来表征各影响因素对环空出口流量变化率的影响程度，该系数越大，该因素对环空出口流量变化率的影响越大。比变异系数计算公式为：

${R_{{{\rm{C}}_{\rm{v}}}}} = \frac{{{C_{v{\rm{f}}}}}}{{{C_{{\rm{v}}x}}}} = \frac{{{\sigma _{\rm{f}}}{m_x}}}{{{m_{\rm{f}}}{\sigma _x}}}$

(21)

式中：R_C_v为比变异系数；C_vf为环空出口流量变化率的变异系数；C_v_x为每个影响因素对应的变异系数；σ_f为环空出口流量变化率的标准差；m_f为环空出口流量变化率的平均值；σ_x为每个影响因素的标准差，量纲与因素本身有关；m_x为每个影响因素的平均值，量纲与因素本身有关。

由于各影响因素之间量纲不一致，进行敏感性分析时需要将各影响因素的原始数值归零化：

${x'_j} = {x_j} - \min ({x_1},{x_2},{x_3} , \cdots )$

(22)

式中：x_j为各影响因素的原始数值；x΄_j为各影响因素归零化的数值。

利用该方法，可以得到突增后环空出口流量变化率的影响因素敏感性分析结果（见图8）。

图 8 突增后的环空出口流量变化率影响因素敏感性分析结果

Figure 8. Sensitivity analysis of influencing factors of change rate after the abrupt increase of annular outlet flow

下载: 全尺寸图片幻灯片

从图8可以看出，对于环空出口流量变化率而言，低密度/高密度钻井液密度差、气侵量、循环排量、分离器位置、井深和井口回压的比变异系数依次减小，敏感性程度也随之降低。因此，在上述因素中，对突增后的环空出口流量变化率影响程度最大的因素是低密度/高密度钻井液密度差。

5. 结论与建议

1）对于新型双梯度钻井，气体前沿到达分离器时，不同参数范围条件下环空出口流量变化率均发生明显突增；当分离器位于泥线以下时，通过监测环空出口流量的突增现象比监测隔水管底端含气率可以更早发现气侵；不同因素对环空出口流量变化率的影响程度有差异，可以通过比变异系数法进行定量分析。

2）文中采用的正常循环井筒温度分布模型，无法精细描述气液两相流时的井筒温度分布及其对气体运移的影响。

3）建议后续开展新型双梯度钻井气侵条件下的井筒温度分布研究，并研制精密的出口流量测量仪器，以完善研究结果，为实现新型双梯度钻井早期气侵监测奠定理论基础、提供数据支持。

图 1 XZ高性能油基钻井液抗岩屑污染评价结果

Figure 1. Evaluation of cuttings pollution resistant of XZ high-performance oil-based drilling fluid

下载: 全尺寸图片幻灯片

图 2 XZ高性能油基钻井液抗地层水污染性能评价结果

Figure 2. Evaluation of formation water pollution resistance of XZ high-performance oil-based drilling fluid

下载: 全尺寸图片幻灯片

图 3 XZ高性能油基钻井液抗水泥污染性能评价结果

Figure 3. Evaluation of cement pollution resistance of XZ high-performance oil-based drilling fluid

下载: 全尺寸图片幻灯片

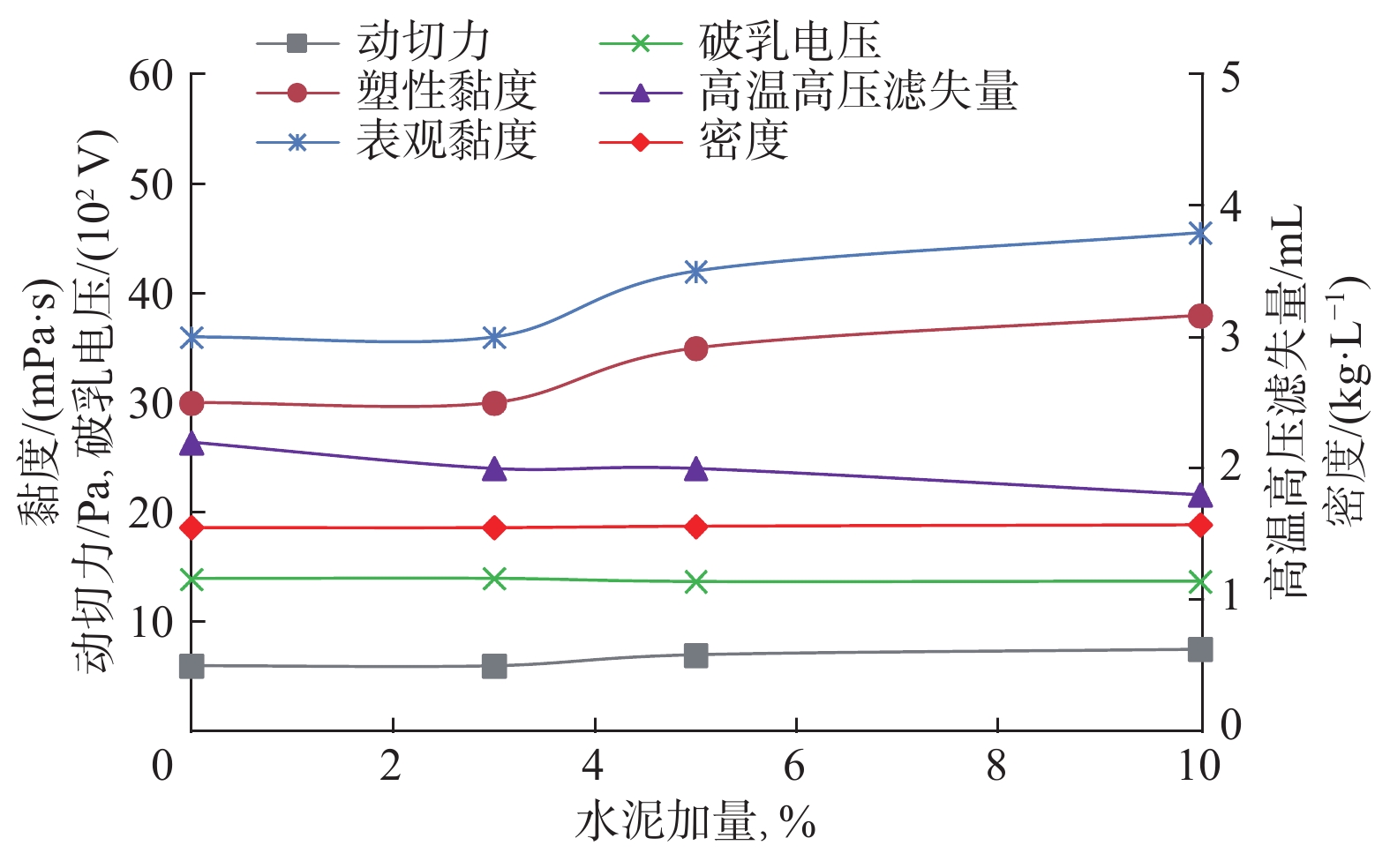
表 1 XZ高性能油基钻井液的加重性能评价结果

Table 1 Evaluation of the weighting performance of XZ high- performance oil-based drilling fluid

密度/ （kg·L^–1）	试验条件	表观黏度/ （mPa·s）	塑性黏度/ （mPa·s）	动切力/Pa	静切力/Pa		高温高压滤失量/mL	破乳电压/ V
密度/ （kg·L^–1）	试验条件	表观黏度/ （mPa·s）	塑性黏度/ （mPa·s）	动切力/Pa	初切	终切	高温高压滤失量/mL	破乳电压/ V
1.35	老化前	30.0	24.0	6.0	3.0	7.0		1 022
1.35	老化后	31.0	25.0	6.0	3.5	6.6	2.2	1 132
1.55	老化前	37.0	30.0	7.0	2.0	5.0		1 103
1.55	老化后	38.0	30.0	8.0	3.0	5.0	2.4	1 308
1.80	老化前	50.0	42.0	8.0	3.0	5.0		1 054
1.80	老化后	51.0	42.0	9.0	3.0	7.0	2.4	1 277
2.01	老化前	60.5	51.0	9.5	4.0	7.0		874
2.01	老化后	63.0	54.0	9.0	4.5	7.0	2.8	1 067
注：老化条件为120 ℃×16 h，流变性测试温度为50 ℃，高温高压滤失量的测试温度为老化温度。

下载: 导出CSV

表 2 XZ高性能油基钻井液的抗高温性能评价结果

Table 2 Evaluation of temperature resistance performance of XZ high-performance oil-based drilling fluid

老化温度/ ℃	表观黏度/ （mPa·s）	塑性黏度/ （mPa·s）	动切力/ Pa	静切力/Pa		高温高压滤失量/mL	破乳电压/ V
老化温度/ ℃	表观黏度/ （mPa·s）	塑性黏度/ （mPa·s）	动切力/ Pa	初切	终切	高温高压滤失量/mL	破乳电压/ V
120	38.0	30.0	8.0	3.0	6.0	2.4	1 350
150	39.0	30.0	9.0	3.0	7.0	2.8	1 312
180	41.0	32.0	9.0	3.0	8.0	3.4	1 098
注：老化时间为16 h，流变性能的测试温度为50 ℃，高温高压滤失量的测试温度为老化温度。

下载: 导出CSV

表 3 XZ高性能油基钻井液的提切性能评价结果

Table 3 Evaluation of shear strength improving performance of XZ high-performance oil-based drilling fluid

配方	试验条件	表观黏度/ （mPa·s）	塑性黏度/ （mPa·s）	动切力/Pa	静切力/Pa		高温高压滤失量/ mL	破乳电压/V
配方	试验条件	表观黏度/ （mPa·s）	塑性黏度/ （mPa·s）	动切力/Pa	初切	终切	高温高压滤失量/ mL	破乳电压/V
基浆	老化前	28.5	25.0	3.5	1.0	4.5		1 455
	老化16 h	30.5	29.0	1.5	2.0	6.5	2.6	1 530
	老化72 h	29.5	27.0	2.5	2.0	4.5	2.8	1 490
基浆+0.5% 提切剂	老化前	33.5	28.0	5.5	3.0	6.0		1 611
	老化16 h	32.0	26.0	6.0	3.5	8.0	2.4	1 900
	老化72 h	34.0	28.0	6.0	4.0	8.0	2.6	1 950
注：基浆为没有加提切剂的XZ高性能油基钻井液；老化温度为120 ℃，流变性能的测试温度为50 ℃，高温高压滤失量的测试温度为老化温度。

下载: 导出CSV

表 4 未加防漏承压材料XZ高性能油基钻井液的封堵承压性能评价结果

Table 4 Evaluation of the sealing and pressure bearing performance of XZ high-performance oil-based drilling fluid free of anti-leakage/pressure-bearing additives

时间/min	不同孔径砂盘的高温高压滤失量/mL					不同孔径砂盘的承压能力/MPa
时间/min	20 μm	40 μm	55 μm	120 μm	150 μm	20 μm	40 μm	55 μm	120 μm	150 μm
1.0	0.2	0.2	0.2	39.2	全滤失	15.0	15.0	15.0	3.0	0
2.5	0.2	0.2	0.2	72.8		15.0	15.0	15.0	3.8
5.0	0.2	0.2	0.3	75.4		15.0	15.0	15.0	4.5
7.5	0.2	0.3	0.3	86.2		15.0	15.0	15.0	5.0
15.0	0.3	0.3	0.3	110.6		15.0	15.0	15.0	6.8
25.0	0.3	0.3	0.3	131.0		15.0	15.0	15.0	5.5
30.0	0.3	0.3	0.3	166.4		15.0	15.0	15.0	8.0
40.0	0.3	0.3	0.3	178.0		15.0	15.0	15.0	7.8
50.0	0.3	0.3	0.3	201.2		15.0	15.0	15.0	8.8
60.0	0.3	0.3	0.3	231.0		15.0	15.0	15.0	9.0
注：老化条件为120 ℃×16 h，流变性测试温度为50 ℃，高温高压滤失量测试温度为老化温度。

下载: 导出CSV

表 5 加入防漏承压材料后XZ高性能油基钻井液的封堵承压性能评价结果

Table 5 Evaluation of sealing and pressure bearing performance of XZ high-performance oil-based drilling fluid after adding anti-leakage/pressure-bearing additives

时间/min	不同孔径砂盘的高温高压滤失量/mL					不同孔径砂盘的承压能力/MPa
时间/min	20 μm	40 μm	55 μm	120 μm	150 μm	20 μm	40 μm	55 μm	120 μm	150 μm
1.0	0.1	0.1	0.1	2.4	1.6	15.0	15.0	15.0	13.5	8.0
2.5	0.1	0.1	0.1	3.0	4.4	15.0	15.0	15.0	15.0	13.5
5.0	0.1	0.1	0.1	3.4	10.2	15.0	15.0	15.0	15.0	13.5
7.5	0.1	0.1	0.1	3.4	18.8	15.0	15.0	15.0	15.0	15.0
15.0	0.1	0.1	0.1	3.4	20.2	15.0	15.0	15.0	15.0	15.0
25.0	0.1	0.1	0.1	3.4	20.8	15.0	15.0	15.0	15.0	15.0
30.0	0.1	0.1	0.1	3.4	21.0	15.0	15.0	15.0	15.0	15.0
40.0	0.1	0.1	0.1	3.4	23.0	15.0	15.0	15.0	15.0	15.0
50.0	0.1	0.1	0.1	3.4	25.8	15.0	15.0	15.0	15.0	15.0
60.0	0.1	0.2	0.2	3.4	26.8	15.0	15.0	15.0	15.0	15.0
注：老化条件为120 ℃×16 h，流变性测试温度为50 ℃，高温高压滤失量测试温度为老化温度。

下载: 导出CSV

表 6 XZ高性能油基钻井液抗低温性能评价结果

Table 6 Evaluation of low temperature resistance performance of XZ high-performance oil-based drilling fluid

温度/℃	试验条件	表观黏度/ （mPa·s）	塑性黏度/ （mPa·s）	动切力/Pa	静切力/Pa		高温高压滤失量/mL	破乳电压/ V
温度/℃	试验条件	表观黏度/ （mPa·s）	塑性黏度/ （mPa·s）	动切力/Pa	初切	终切	高温高压滤失量/mL	破乳电压/ V
120	老化前	37.0	30.0	7.0	3.0	6.0		1 018
120	老化16 h后	39.5	32.0	7.5	3.5	6.0	2.2	985
–24	冷冻72 h，0 ℃测	125.0	120.0	5.0	5.0	7.5	1.8	869
–24	冷冻72 h，50 ℃测	45.0	36.0	9.0	4.0	7.0	1.8	1 243
注：高温高压滤失量测试温度为120 ℃。

下载: 导出CSV

表 7 4口应用井XZ高性能油基钻井液基本性能

Table 7 Performance statistics of XZ high-performance oil-based drilling fluids in 4 wells of 2 platforms

井号	密度/（kg·L^–1）	漏斗黏度/s	塑性黏度/ (mPa·s)	动切力/Pa	静切力/Pa		高温高压滤失量/mL	破乳电压/V	ϕ6读数
井号	密度/（kg·L^–1）	漏斗黏度/s	塑性黏度/ (mPa·s)	动切力/Pa	初切	终切	高温高压滤失量/mL	破乳电压/V	ϕ6读数
MDHW2107	1.50～1.55	52.0～68.0	25.0～30.0	4.0～9.0	1.0～4.0	4.0～10.0	1.2～1.8	1120～2047	4～7
MDHW2114	1.50～1.55	58.0～70.0	25.0～29.0	6.0～10.0	1.0～3.0	4.0～11.0	1.6～2.0	1350～2047	5～7
MDHW2108	1.50～1.55	58.0～64.0	26.0～34.0	8.0～12.0	2.0～3.5	7.0～12.0	1.4～2.0	610～2047	3～7
MDHW2109	1.50～1.55	68.0～76.0	26.0～32.0	7.0～11.0	2.0～3.0	8.0～12.0	0.5～1.2	936～2047	3～7
注：高温高压滤失量测试温度为120 ℃。

下载: 导出CSV

表 8 XZ高性能油基钻井液与常规水基钻井液现场应用效果对比

Table 8 Comparison on the application effects of XZ high-performance oil-based drilling fluid and the conventional water-based drilling fluids

钻井液	机械钻速/(m·h^–1)		钻井周期/d
钻井液	造斜段	水平段	钻井周期/d
常规水基钻井液	1.93	3.75	65.5
XZ高性能油基钻井液	3.30	7.02	38.0

下载: 导出CSV

参考文献(11)

[1]	路宗羽,赵飞,雷鸣,等. 新疆玛湖油田砂砾岩致密油水平井钻井关键技术[J]. 石油钻探技术, 2019, 47(2): 9–14. LU Zongyu, ZHAO Fei, LEI Ming, et al. Key technologies for drilling horizontal wells in glutenite tight oil reservoirs in the Mahu Oilfield of Xinjiang[J]. Petroleum Drilling Techniques, 2019, 47(2): 9–14.
[2]	秦文政,党军,臧传贞,等. 玛湖油田玛18井区“工厂化”水平井钻井技术[J]. 石油钻探技术, 2019, 47(2): 15–20. QIN Wenzheng, DANG Jun, ZANG Chuanzhen, et al. Factorization drilling technology of the horizontal well in the Ma18 well block of the Mahu Oilfield[J]. Petroleum Drilling Techniques, 2019, 47(2): 15–20.
[3]	王海涛,张伟,王国斌,等. 准噶尔盆地环玛湖凹陷钻井提速技术[J]. 石油钻采工艺, 2014, 36(4): 30–33. WANG Haitao, ZHANG Wei, WANG Guobin, et al. ROP enhancing technology for circum-mahu lake depression in Junggar Basin[J]. Oil Drilling & Production Technology, 2014, 36(4): 30–33.
[4]	李洪,邹灵战,汪海阁,等. 玛湖致密砂砾岩2 000 m水平段水平井优快钻完井技术[J]. 石油钻采工艺, 2017, 39(1): 47–52. LI Hong, ZOU Lingzhan, WANG Haige, et al. High-quality fast drilling and completion technologies for horizontal wells with horizontal section of 2 000 m long in Mahu tight glutenites[J]. Oil Drilling & Production Technology, 2017, 39(1): 47–52.
[5]	于洋飞,杨光,陈涛,等. 新疆玛湖区块2 000 m长水平段水平井钻井技术[J]. 断块油气田, 2017, 24(5): 727–730. YU Yangfei, YANG Guang, CHEN Tao, et al. Drilling technology of 2 km-long horizontal section in Mahu Block, Xinjiang Oilfield[J]. Fault-Block Oil & Gas Field, 2017, 24(5): 727–730.
[6]	谢军,何勇,王安鹤,等. 克拉玛依油田八区调整井钻井液技术[J]. 钻井液与完井液, 2007, 24(1): 88–91. XIE Jun, HE Yong, WANG Anhe, et al. Drilling fluid technology used in drilling adjustment wells in Block 8 in Karamay Oilfield[J]. Drilling Fluid & Completion Fluid, 2007, 24(1): 88–91.
[7]	吴江,李龙,任冠龙,等. 海上复杂易垮塌地层高性能油基钻井液研发与应用[J]. 钻井液与完井液, 2018, 35(5): 55–60. WU Jiang, LI Long, REN Guanlong, et al. Development and application of a high performance oil base drilling fluid for drilling complex sloughing formations in offshore operations[J]. Drilling Fluid & Completion Fluid, 2018, 35(5): 55–60.
[8]	王中华. 国内钻井液技术进展评述[J]. 石油钻探技术, 2019, 47(3): 95–102. WANG Zhonghua. Review of progress on drilling fluid technology in China[J]. Petroleum Drilling Techniques, 2019, 47(3): 95–102.
[9]	何振奎. 泌页 HF1井油基钻井液技术[J]. 石油钻探技术, 2012, 40(4): 32–37. HE Zhenkui. Oil base drilling fluid technology applied in Well Biye HF 1[J]. Petroleum Drilling Techniques, 2012, 40(4): 32–37.
[10]	林永学,王显光. 中国石化页岩气油基钻井液技术进展与思考[J]. 石油钻探技术, 2014, 42(4): 7–13. LIN Yongxue, WANG Xianguang. Development and reflection of oil-based drilling fluid technology for shale gas of sinopec[J]. Petroleum Drilling Techniques, 2014, 42(4): 7–13.
[11]	王显光,李雄,林永学. 页岩水平井用高性能油基钻井液研究与应用[J]. 石油钻探技术, 2013, 41(2): 17–22. WANG Xianguang, LI Xiong, LIN Yongxue. Research and application of high performance oil base drilling fluid for shale horizontal wells[J]. Petroleum Drilling Techniques, 2013, 41(2): 17–22.

施引文献(10)

期刊类型引用(7)

1.	蒋振新，李军，郭勇，吴德胜，时培忠，杨宏伟，张更. 井下双梯度控压钻井井筒多相流动规律. 断块油气田. 2024(05): 936-944 . 百度学术
2.	鲁义攀，魏勇，陈强，刘国权，刘杰. 基于热传导时域积分的井下流量测量方法. 石油钻探技术. 2023(01): 106-114 . 本站查看
3.	王江帅，李牧，翟文宝，何岩峰，邓嵩. 气侵条件下深水变梯度控压钻井泥浆池增量变化规律. 常州大学学报(自然科学版). 2023(04): 87-92 . 百度学术
4.	祝效华，冉亮，敬俊，孙汉文，王成涛，张一鹏. 隔水管充气双梯度钻井充气水深和充气速率研究. 石油钻探技术. 2022(01): 22-29 . 本站查看
5.	姜瑞海，崔云峰，张晨，陈勋. 页岩气偏心水平井气侵期间岩屑运移数值模拟. 科技和产业. 2022(06): 283-289 . 百度学术
6.	张洁，汤明，蒋振新，甘一风，曾德智. 椭圆井眼同心环空赫巴流体流动规律研究及压降计算简化模型. 特种油气藏. 2021(02): 156-162 . 百度学术
7.	王江帅，李军，何岩峰，柳贡慧，邓嵩，杨宏伟，宋学锋，杨青，夏顺雷. 变梯度控压钻井井控过程中井口回压变化规律. 石油学报. 2021(11): 1499-1505 . 百度学术

其他类型引用(3)

资源附件(0)

图(3) / 表(8)

计量

文章访问数: 752
HTML全文浏览量: 261
PDF下载量: 102
被引次数: 10

1. 气液两相流模型的建立
1.1 物理模型
1.2 气液两相流数学模型
1.2.1 质量守恒方程
1.2.2 动量守恒方程
1.3 辅助方程
1.3.1 漂移流模型
1.3.2 摩阻压降模型
1.3.3 环空流体密度分布
1.3.4 气体前沿位置及气侵量确定方法
2. 模型求解
2.1 初始边界条件
2.2 模型离散结果
2.3 求解步骤
3. 气侵条件下环空出口流量的影响因素分析
3.1 井深
3.2 气侵量
3.3 分离器位置
3.4 低密度/高密度钻井液密度差
3.5 排量
3.6 井口回压
4. 环空出口流量变化率影响因素敏感性分析
5. 结论与建议

1. 气液两相流模型的建立
1.1 物理模型
1.2 气液两相流数学模型
1.2.1 质量守恒方程
1.2.2 动量守恒方程
1.3 辅助方程
1.3.1 漂移流模型
1.3.2 摩阻压降模型
1.3.3 环空流体密度分布
1.3.4 气体前沿位置及气侵量确定方法
2. 模型求解
2.1 初始边界条件
2.2 模型离散结果
2.3 求解步骤
3. 气侵条件下环空出口流量的影响因素分析
3.1 井深
3.2 气侵量
3.3 分离器位置
3.4 低密度/高密度钻井液密度差
3.5 排量
3.6 井口回压
4. 环空出口流量变化率影响因素敏感性分析
5. 结论与建议

参考文献(11)

施引文献(10)

资源附件(0)

准噶尔盆地玛东油田水平井高性能油基钻井液技术

作者简介: 张雄（1979—），男，湖北黄梅人，2003年毕业于江汉石油学院化学工程与工艺专业，高级政工师，主要从事项目管理工作。E-mail：89227198@qq.com

计量

出版历程

High-Performance Oil-Based Drilling Fluid Technology for Horizontal Wells in the Madong Oilfield, Junggar Basin

1. 气液两相流模型的建立

1.1 物理模型

1.2 气液两相流数学模型

1.2.1 质量守恒方程

1.2.2 动量守恒方程

1.3 辅助方程

1.3.1 漂移流模型

1.3.2 摩阻压降模型

1.3.3 环空流体密度分布

1.3.4 气体前沿位置及气侵量确定方法

2. 模型求解

2.1 初始边界条件

2.2 模型离散结果

2.3 求解步骤

3. 气侵条件下环空出口流量的影响因素分析

3.1 井深

3.2 气侵量

3.3 分离器位置

3.4 低密度/高密度钻井液密度差

3.5 排量

3.6 井口回压

4. 环空出口流量变化率影响因素敏感性分析

5. 结论与建议

期刊类型引用(7)

其他类型引用(3)

计量

出版历程

目录

1. 气液两相流模型的建立

1.1 物理模型

1.2 气液两相流数学模型

1.2.1 质量守恒方程

1.2.2 动量守恒方程

1.3 辅助方程

1.3.1 漂移流模型

1.3.2 摩阻压降模型

1.3.3 环空流体密度分布

1.3.4 气体前沿位置及气侵量确定方法

2. 模型求解

2.1 初始边界条件

2.2 模型离散结果

2.3 求解步骤

3. 气侵条件下环空出口流量的影响因素分析

3.1 井深

3.2 气侵量

3.3 分离器位置

3.4 低密度/高密度钻井液密度差

3.5 排量

3.6 井口回压

4. 环空出口流量变化率影响因素敏感性分析

5. 结论与建议

作者简介:
张雄（1979—），男，湖北黄梅人，2003年毕业于江汉石油学院化学工程与工艺专业，高级政工师，主要从事项目管理工作。E-mail：89227198@qq.com